基于chirplet的弹道目标逆合成孔径雷达回波分解

金光虎 高勋章 黎 湘 陈永光

①(国防科技大学电子科学与工程学院 长沙 410073)②(中国人民解放军63880部队 洛阳 471003)

1 引言

ISAR成像质量是决定目标识别准确度的关键，为了提高弹道目标识别率，实现精确拦截，宽带雷达首先必须获得清晰的ISAR图像。ISAR成像通常采用距离多普勒(Range Doppler，RD)算法，该算法要求目标转动的角度较小，对于弹道目标而言，随自旋变化的尾翼、安装螺帽等尾附体回波不满足成像条件，尾附体回波的存在严重影响主体的ISAR成像质量，提高成像质量的关键是将尾附体回波从雷达回波中分离。

针对ISAR成像中信号分离问题，文献[1-3]提出了距离像域分解方法，将单个距离单元信号分解为一系列线性调频信号，并根据中心频率和调频率分布进行信号分离。文献[1]通过chirplet分解分离了旋转部件的微多普勒，得到了飞机ISAR像和人行走时手摆动的周期特征。文献[2]使用相消处理和微多普勒剔除得到了飞机复杂运动时的ISAR像。文献[3]分析了平动、转动、振动的微多普勒特性，分离了多种不同微动信号，实现了ISAR成像。

本文提出了一种新的弹道目标回波分解方案，根据LFM回波特性构建了慢时间域单频信号回波，对回波的多普勒分析表明，尾附体回波在时频域近似为杂波。本文采用chirplet分解可以直接分离主体回波，将主体回波表示为若干高斯包络的线调频分量矢量和。与传统距离像域分解方法相比，慢时间域分解能够避免距离像域信号不完整带来的分解错误，分解更加准确；不需要根据回波分量的特点进行分类，分解过程更加简单，仿真试验结果表明，主体回波和尾附体回波能够较好分离，弹道目标ISAR成像质量具有明显提高。

2 弹道目标宽带雷达回波信号

2.1 弹道目标散射特性及运动特性分析

空间弹道目标是一类较为特殊的空间目标，在目标外形、运动姿态上与空间站、卫星等空间目标具有较大差异。弹道目标的主体通常是由锥、柱、台等旋转对称体构成；安装、固定的需要使得目标表面还存在螺帽等部件，为了增加飞行的稳定性，有的目标在尾部增加了尾翼，本文将尾翼、螺帽等统称为尾附体。弹道目标的另一个特点是运动较为复杂，为了保持一定的攻角，弹道目标通常采用自旋定向，由于不可避免的横向扰动力的影响，目标会产生进动[4]，即绕对称轴旋转的同时绕进动轴旋转，弹道目标外形及自旋、进动示意图如图1所示。

图1 弹道目标外形及进动示意图

弹道目标主体是较为特殊的一类形体，绕对称轴的旋转不会改变目标外形，因此，在雷达照射下，散射场也不会因为自旋而变化，这种情况下目标的3维姿态转动可以等效为单自由度转动，即雷达回波仅受雷达视线和目标对称轴夹角的这一个变化量的影响，根据凯勒几何绕射理论的局部场原理，弹道目标可以采用散射中心模型近似[5]，每个散射中心相当于斯特拉顿-朱(Stratton-Chu)积分中的一个不连续处，从几何观点分析，就是一些曲率不连续处与表面不连续处，对于弹道目标而言，强散射中心位于包含对称轴的切平面上，散射中心位于该切面的不连续处。图2是主体的散射中心模型。

图2 典型弹道目标外形及散射中心模型

尾附体的散射为目标上的局部散射，散射中心位置与尾附体的实际位置相对应。因此，该部分的散射中心位置随着自旋而发生改变。弹道目标散射回波可以视为主体及尾附体回波的合成，文献[6]分析了旋转对称体的散射特性，根据该文，具有旋转对称结构的主体回波仅受雷达视线和目标对称轴角度变化影响。由于进动是一种小角度慢速旋转，主体部分仍然可以通过距离多普勒成像算法或距离瞬时多普勒成像算法得到ISAR像，但是，由于尾翼、安装螺钉等尾附体部件对应的散射中心参与了自旋运动，由于自旋频率通常达到几赫兹，距离多普勒成像条件难以满足，直接对弹道目标进行成像必然会造成成像模糊。

2.2 弹道目标宽带雷达回波模型

本文以常见的宽带LFM体制的宽带成像雷达为例，对主体和杂波分别建模。根据文献[7]，线性调频体制的雷达，在“停-走-停”模型下目标回波可以表述为

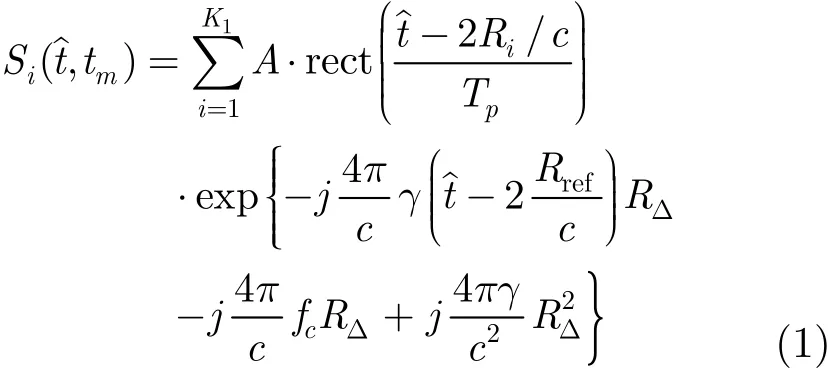
其中Ri为散射点到雷达的距离，Rref为参考距离，RΔ=Ri-Rref，为快时间，对应的时间起点为发射时刻，tm为慢时间，tm=mT，m=1,2,⋅⋅⋅，T为脉冲重复周期。

从式(1)可知，建立回波模型的关键是确定散射点与参考位置的距离RΔ。对主体而言，目标的自旋不改变散射场，只需要考虑进动对目标回波的影响，进动可以分解为目标在雷达视线与进动轴所在平面内的旋转和目标绕雷达视线方向的旋转(非正交分解)，其中绕雷达视线方向的旋转不改变散射点在雷达视线方向的投影位置，目标姿态可以用一个参量表示，即目标对称轴和雷达视线的夹角ψ(tm)，建立回波模型的关键是该角度的大小，设主体的散射中心数目为K1，为了计算方便，以雷达视线和进动轴所在平面为xpyp平面，以进动轴为yp轴建立右手3维坐标系，如图3所示。

进动轴方向和雷达视线方向的夹角为ϕl，在t0+tm时刻，目标绕进动轴转过角度ϑ=ωptm，所以t0+tm时刻对应的雷达视线和目标对称轴的夹角为

图3 弹道目标主体姿态角随时间变化关系

因为进动角较小，通常为5º-10º，ψ(τ)的波动范围较小，可以用直线方程近似。考虑起始相位的不确定性，雷达视线和目标主轴的角度可以表示为

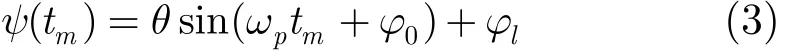
假设目标主体上有一个散射点P，在以对称轴为y轴的直角坐标系中坐标为(x, y)，则散射点在该段时间内任意时刻的RΔ(t)可以表示为

由于进动角较小，ψ(tm)变换范围较小，令采用一阶近似可得

尾附体分量主要包括安装螺钉、尾翼等部件回波，与主体部分的散射场不同的是，该部分的散射中心参与了自旋和进动两种运动，其中进动可以等效为雷达视线与进动轴所在平面内的转动，尾附体的运动可以等效为进动与自旋的合成，下面进一步分析由自旋引起的散射点位置随时间变化关系。设尾附体等效散射中心数目为K2，散射中心与质心的距离为Lk，所在旋转平面内半径为rk，以目标质心为原点，以旋转对称平面为xy平面，建立目标本体坐标系，如图4所示。设自旋转过角度为则散射中心在本体坐标系中的坐标为

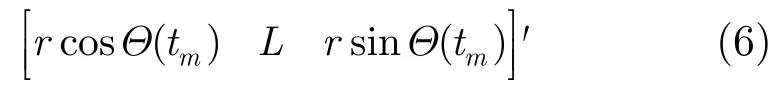
根据坐标系变换关系，在雷达视线上的投影位置为

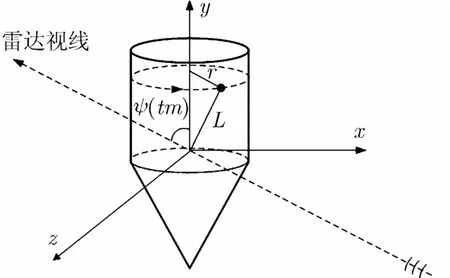
图4 尾附体进动、自旋等效模型

将式(3)代入式(7)，由于θ较小，通常只有几度，采用一阶近似可得

将式(5)和式(8)代入式(1)，可分别得到主体和尾附体回波。从距离随慢时间变化中可知，回波中主体回波受进动调制，尾附体回波受进动和自旋调制，由于进动角较小，进动周期较大，自旋频率较大，主体回波在一定时间内仍然满足小角度成像条件，但是，尾附体回波受自旋频率调制，变化较快，不满足小角度成像条件，势必导致成像模糊。为了能够得到清晰的主体部分的ISAR像，必须将主体和尾附体回波进行分离。

3 基于chirplet的主体尾附体散射回波分解

3.1 慢时间域单频回波构建及频谱分析

宽带雷达回波成像前可以通过补偿算法补偿掉式(1)中的第2项第3项，由于每次回波解调频使用的参考中心不一致带来的误差也可以通过包络对齐和相位自聚焦补偿掉，补偿后雷达回波可视为转台回波。固定，令fi=fc+(-2Rref/c)，忽略高次相位项，则式(1)可以表示成单频信号形式：

根据前面的推导，分别将式(5)和式(8)代入式(9)，可得主体和尾附体回波形式为

目标回波为主体和尾附体两部分回波的合成，可以表示为

为了分析这两类信号的特性，首先求解其多普勒频率，主体部分的瞬时多普勒频率为

尾附体回波的瞬时多普勒频率为

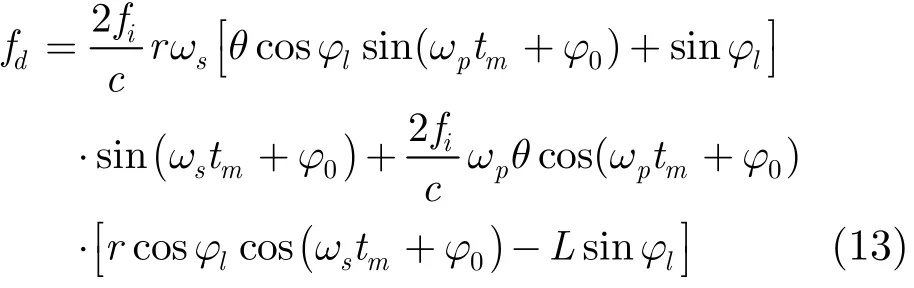
首先分析尾附体的瞬时多普勒频率，由于θ≪1，ωp＜＜ωs，式(13)所示的多普勒频率fd中，第一项远大于其他两项，以进动角为0.1 rad、自旋频率为3 Hz(角速度为6π rad/s)、半径为r=1 m、频率为9×109Hz计，该分量的最大值约为1000 Hz，以雷达脉冲重复周期为300 Hz计算，尾附体回波的多普勒频率远大于脉冲重复频率，这样的信号在时频面内是不能分辨的。以同样的数值分析主体的多普勒频率，其多普勒大概在数十赫兹，远小于脉冲重复频率，图5(a)是主体部分雷达回波的时频图，图5(b)是尾附体雷达回波的时频图，从图中可以看出由于自旋频率较快，尾附体回波时频图分布较为杂乱，证实了本文的理论分析。

3.2 基于chirplet的信号分离

chirplet分解是近年来发展起来的一种优秀分解算法[8,9]，与时频变换、傅里叶变换等方法相比，chirplet分解能够方便地实现信号在二阶相位上的分解与重构，将信号近似为高斯包络的线性调频信号和，在分析和重构具有二阶相位变化的信号方面具有傅里叶变换、时频变换等方法不可比拟的优势。本文利用chirplet的这一特点，将弹道目标雷达回波分解为若干个线性调频信号矢量和，实现了主体回波重构。

chirplet基函数可以表示如下：

chirplet基函数是能够正确描述雷达信号模型的众多基函数中的一种，但是该基函数也有着其他许多基函数不具有的优点。首先，对于前面提到了雷达信号只需要一定参数的基函数即可表示；第2，该基函数仅包含4个参量，计算量不致太大；第3是chirplet适用于分解主体和尾附体转速不同这样的雷达信号，这是因为chirplet的相位实际上包含了二次相位信息，虽然转动目标的相位是以三角函数形式出现的，在短时间内仍可近似为线性调频信号，采用二阶相位形式的chirplet来近似回波信号是合理的，在一定精度范围内能够满足信号分离和重构的要求。

对于本文的研究对象，尾附体回波的多普勒频率远大于脉冲重复频率，在慢时间域进行分析，该值大于脉冲重复频率，即该部分的信号是欠采样的，因此该部分信号不满足分解及重构条件，只有主体部分满足这一条件，因此chirplet分解将得到主体回波在多普勒、多普勒率2维平面上的分解表示，欠采样的尾附体回波被保留在剩余信号中，对主体回波进行重构，尾附体回波可以通过从原始回波中分离主体回波间接得到。

3.3 信号分解及重构的具体实现步骤

本文采用自适应chirplet分解对雷达回波进行分解，设宽带雷达回波采样率为fs，共得到N个采样点，脉冲重复频率为prf，共得到M个脉冲回波，对其进行自适应chirplet分解和重构的具体步骤为

第1步 设定快时间采样索引n=1，快时间t=(n−N/2)/fs。

第2步 设定索引k=1，慢时间序列tm=(m−M/2)/prf ，m∈[1,M]，剩余信号Rk(tm)为S( t, tm)。

第3步 通过chirplet对Rk(tm)进行分解，寻找该信号在下面基函数上投影的最大值

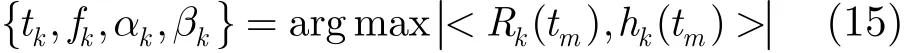
其中＜Rk(tm),hk(tm)＞定义为

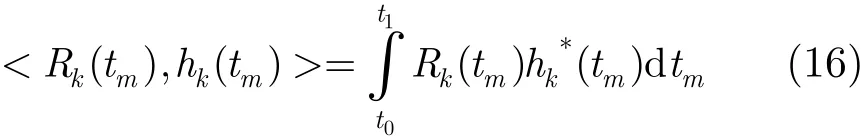
第5步 设分解得到K个谐波信号为

对应的谐波分解系数为ck为

对主体回波和尾附体回波进行重构，重构后的回波表达式为

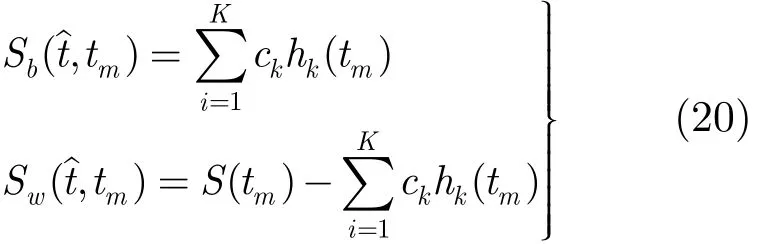
第6步 若n=N，分解及重构过程结束，否则令n=n+1，转至步骤2。

上述过程中的关键步骤是寻找信号在基函数上投影的最大值，由于需要在4维空间中进行搜索，计算量较大，文献[10]提出了快速算法，设置4个参量的初始值，通过搜索迭代方式寻找最优的参数得到投影的最大值，具有较高的计算效率，本文后续计算基于这一快速算法。

4 实验与结果

为了验证本文算法，本文针对有翼弹道目标的线调频雷达回波进行了实验，目标飞行场景及目标外形如图6(a)，图6(b)所示，目标的尾部有4个尾翼，均匀分布。以地心为原点，以弹道平面为xy平面建立地心惯性坐标系，雷达在该坐标系中的坐标为(356×103, 6350×103, 19×103) m，关机点坐标为(-1850×103, 6440×103, 0) m，关机点速度(4×103,4×103, 0)m/s，目标共飞行13 min 40 s，从关机点开始到弹着点飞行距离为3911 km。目标自旋频率为3 Hz，进动周期为2.03 s，进动角为10.0º，雷达带宽1 GHz，脉宽100 μs，采样率1 MHz，脉冲重复频率300 Hz。

观测从目标关机后100 s开始，观测时间长度为1 s，得到的1维距离像为图7(a)所示，采用RD成像算法得到ISAR图像如图7(b)所示。

在平动补偿和相位校正后返回到原始数据域，根据第3节构建慢时间域单频回波，对其进行chirplet分解，图8(a)给出了快时间=50 μs时慢时间域回波分解前时频图，图8(b)给出了重构后的主体回波时频图。

采用本文方法对每一采样点进行分离后，重构主体和尾翼回波，距离向压缩得到主体部分的距离像序列如图9(a)所示，尾附体的距离像序列如图9(b)所示。

从图(9)中可以看出，主体和尾翼回波基本被分离，进一步根据原始回波RD成像和重构的主体回波RD成像结果如图10(a)所示，图10(b)是采用距离像域分解方法得到的主体回波成像结果。

对比图10(a)和图7(b)，本文方法可以较好改善弹道目标ISAR成像质量，对比距离像域的分解结果，由于信号丢失较小，成像质量也会有一定幅度的提高。进一步采用不同时间段的数据进行分解、成像，成像质量较分离前均有较大程度的提高，验证了本文算法的有效性。

图5 主体回波的时频图和尾附体回波的时频图

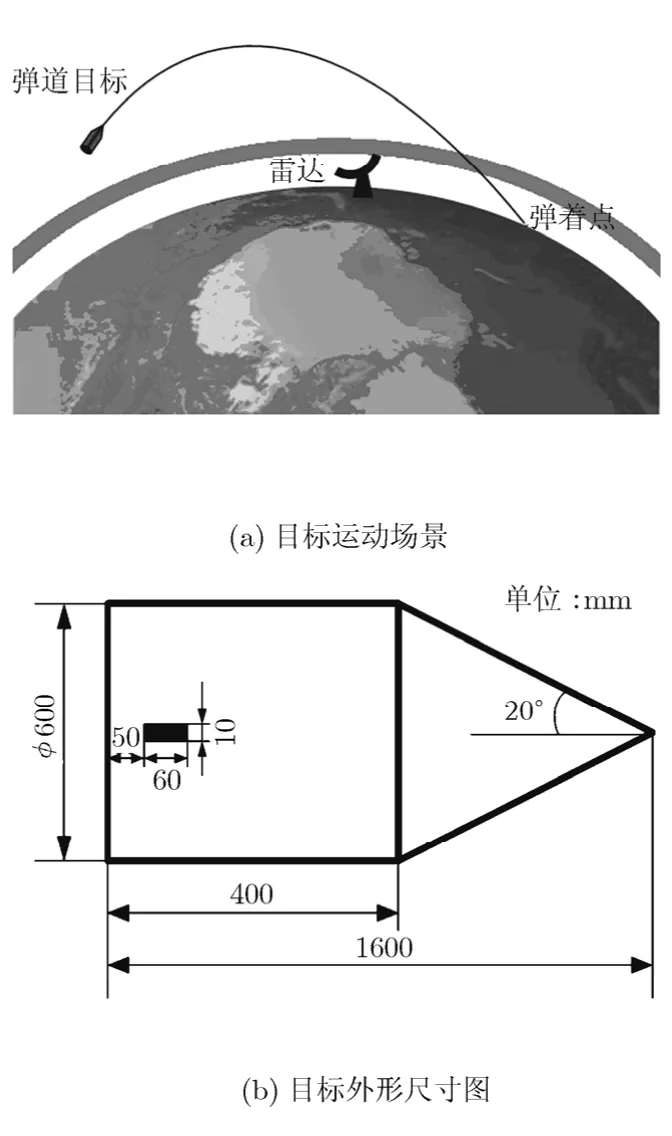
图6 弹道目标运动场 景及目标外形尺寸图

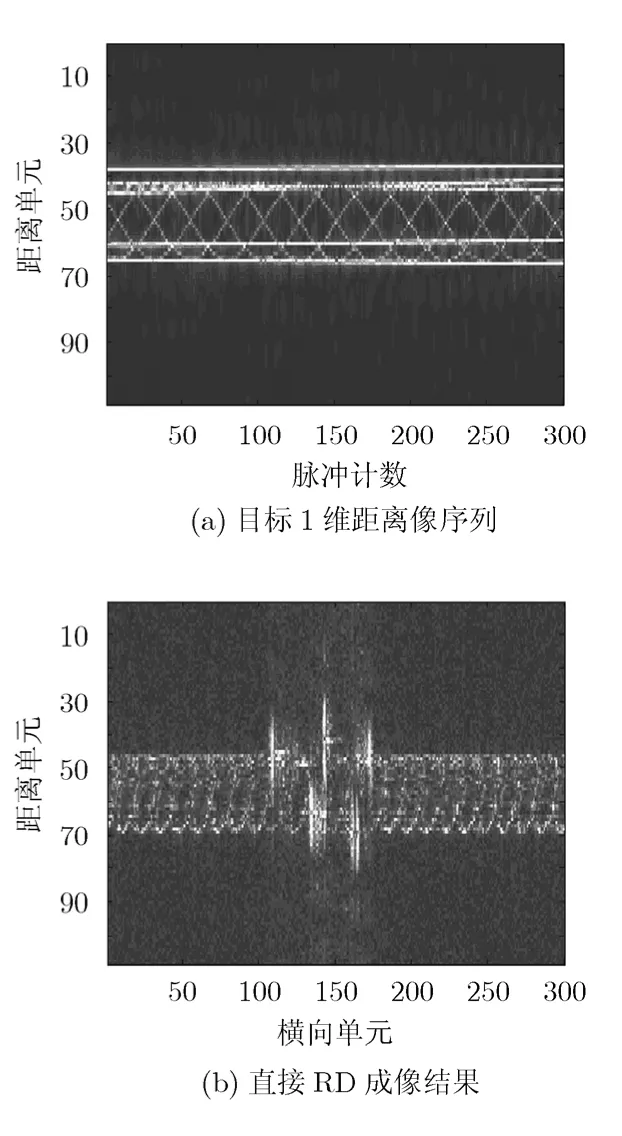
图7 目标1维距离像序 列及直接RD成像结果

5 结论

本文根据中段弹道目标的特点提出了基于chirplet的弹道目标信号分离方法，算法改变了传统的距离像域分解方式，根据LFM信号特点，构建了慢时间域单频回波信号，在慢时间域进行分解，避免了距离像域分解由于越距离单元走动带来的分解错误，给出了具体的分解、重构步骤，仿真实验表明，尾附体分离后成像效果具有明显提高，验证了本文算法的有效性。

图8 某频率点上的回波时频图和重构后主体回波时频图

图9 重构的主体和尾翼部分距离像序列

图10 本文方法及距离像域 分解方法ISAR成像结果

[1] Li J and Ling H. Application of adaptive chirplet representation for ISAR feature extraction from targets with rotating parts[J]. IEE Proceeding Radar Sonar Navigation,2003, 150(4): 284-291.

[2] 罗迎, 张群, 封同安等. 强杂波下含旋转部件的目标成像及微多普勒提取[J]. 系统工程与电子技术, 2008, 31(2): 261-264.Luo Ying, Zhang Qun, and Feng Tong-an, et al.. Imaging and micro-Doppler extraction of targets with rotating parts in strong ground clutter[J]. System Engineering and Electronics,2008, 31(2): 261-264.

[3] 李斌, 姚康泽, 王岩等. 基于微动分析和chirplet分解的ISAR成像[J]. 信号处理, 2009, 25(2): 264-269.Li Bin, Yao Kang-ze, and Wang Yan, et al.. ISAR based on micro-motion analysis and chirplet separation[J]. Signal Processing, 2009, 25(2): 264-269.

[4] 陈行勇, 黎湘, 郭桂蓉等. 微进动弹道导弹目标雷达特征提取[J]. 电子与信息学报, 2006, 28(4): 643-646.Chen Hang-yong, Li Xiang, and Guo Gui-rong, et al.. Radar feature extraction of micro-precession ballistic missile warhead[J]. Journal of Electronics & Information, 2006, 28(4):643-646.

[5] 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 电子工业出版社, 2005: 230-237.

[6] 金光虎, 朱玉鹏, 高勋章等. 基于一维像序列的中段雷达目标进动特征提取[J]. 信号处理, 2009, 25(4): 771-776.Jin Guang-hu, Zhu Yu-peng, and Gao Xun-zhang, et al..Precession feature extraction of midcourse radar target based on HRRP series[J]. Signal Processing, 2009, 25(4): 771-776.

[7] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 电子工业出版社,2005: 24-25.

[8] Qian S, Chen D, and Yin Q. Adaptive chirplet based signal approximation[J]. Proceeding ICASSP, Seattle, WA, 1998:1871-1874.

[9] Lu Yu-feng, Oruklu Erdal, and Saniie Jafar. Fast chirplet transform with FPGA-based implementation[J]. IEEE Transactions on Signal Processing, 2008, 15(6): 577-580.