基于速调管2.5维粒子模型的非线性注波互作用的研究

高冬平 丁耀根 刘濮鲲 杜朝海 赵 鼎

①(中国科学院电子学研究所中国科学院高功率微波源与技术重点实验室 北京 100190)②(中国科学院研究生院 北京 100039)

1 引言

速调管自1939年问世以来，作为一种高功率、高增益和高效率的微波放大器件，已经在科学研究、国防建设和工业生产等诸多领域得到了广泛的应用。速调管工作稳定可靠，使用寿命长，在大功率微波应用领域有着不可替代的作用。但是，速调管的工作机理很复杂，实际研究过程中通常依靠多次制作实验样管来修正设计，不仅研制周期长，而且耗资巨大。为更加准确地设计速调管，国内外的许多研究机构开发出一系列模拟软件，比如基于1维(1D)模型的KLY6，JPNDSK；基于2.5维(2.5D)模型的FCI[1]，Arsenal. MSU，中国科学院电子所的LSP[2]，TESLA[3]，和Magic2D[4]；以及基于3维(3D)模型的Magic3D[4,5]。1维模型通常采用圆盘模型。该模型忽略了电子的径向运动和电子间的径向作用力，认为每个圆盘中包含的电子具有全同的运动状态。1D模型能较好地模拟聚焦良好且电子注波动小的速调管。但是对于导流系数较高，电子注波动较大的速调管，电子的径向运动已经不可忽略，故此时得到的模拟结果与实测值偏离较大。3维粒子模拟程序(PIC：Particle-In-Cell simulation)可以完全考虑粒子在3个方向的运动信息，通过求解全3维的Maxwell方程来推进粒子的运动。理论上讲，该方法最接近速调管的实际物理情形。然而，3维粒子模型由于是全时域粒子模拟代码，需要巨大的计算资源，这严重影响该模型的实用性。

常规的速调管具有轴对称结构，可以忽略电子的角向运动对互作用系统的影响，从而将全3维模型简化为2.5D(2维位移，3维速度)模型。此外对于导流系数较大、电子注径向波动较剧烈的情形，2.5D粒子模型能够准确地考虑电子的径向运动，很好地处理漂移管壁对电子的截获，全面准确地分析输出腔入口和出口位置处电子注的群聚状态和电子注的运动电流。这些问题都是1维模型所不能处理的。现有的大多数2.5D模型都是基于端口近似的频域稳态模型，不能研究系统的瞬态变化过程；此外Magic2D采用全数值的时域模型，虽然能够较全面地模拟轴对称结构的互作用系统，但是消耗资源较大，运算时间太长，缺乏实用性。本文改进的2.5D模型是一个将端口近似和PIC相结合的时域粒子模型。该模型可以模拟互作用系统随时间的演化过程，从而有助于分析谐振腔间隙电压从开始建立至达到稳定的复杂过程；同时，由于采用端口近似模拟高频谐振腔，减少了高频场的计算时间，比全数值的Magic2D高效，更具有实用性。

本文将着重介绍用于研究速调管中复杂注波互作用过程的2.5D粒子模型。该模型是首次将端口近似方法和PIC结合起来的时域粒子模型。大量的研究表明端口近似方法能够比较准确地模拟谐振腔对互作用系统的影响[1−4]，所以该模型具有高效、准确和节省计算资源等优点。在每一个时间步中，该模型可以选择采用面积权重或体积权重将粒子电荷恰当地分配到空间网格各点上，再根据电流连续性方程将电流分配到网格各边上；采用时域有限差分方法求解麦克斯韦方程组以精确解出电子注在漂移管中产生的空间电荷场；采用端口近似来模拟高频谐振腔场，谐振腔场分布可以采用解析场(漂移头间隙电场分布采用双曲余弦函数近似表示)或数值场(通过Superfish或CST等软件仿真求得)两种形式；最后，采用Boris旋动格式求解洛伦兹力方程来更新粒子的速度和位置，并在柱坐标系下对粒子的速度推进作了修正。C++语言特有的类设计也使得KLY2D具有很强的扩展性，它提供了多种模拟边界，有金属边界、对称轴边界和漂移管右端的吸收边界。本文将在最后给出对具体速调管实例的计算结果与相关讨论。

2 物理模型

2.1 运动粒子电荷与电流的PIC分配

电荷PIC分配采用面积加权[6]的算法来处理，具体过程如图1所示。设该宏粒子所处的位置为xn，格点1所占的面积为a，格点2所占的面积为b，格点3所占的面积为c，格点4所占的面积为d，轴、径向的网格步长分别为hz，hr，该网格总面积为S=h⋅h，另外再定义= (xn−)⋅z0，zr=(xn−xj,k)⋅r0，其中z0、r0分别为z、r方向的单位向量。

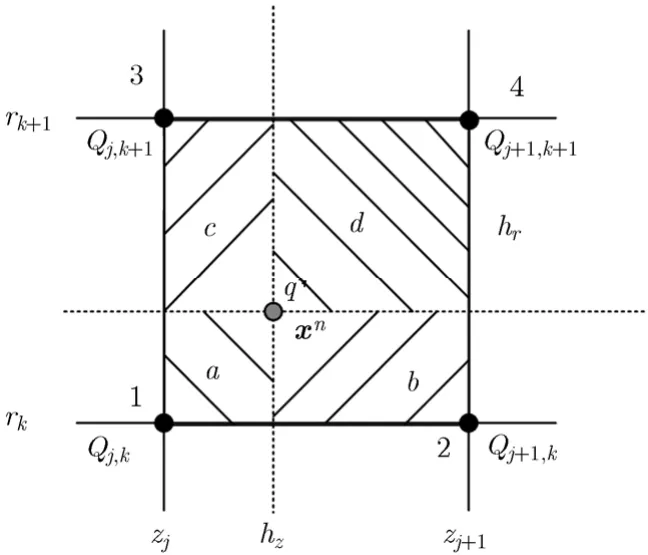
图1 PIC电荷分配到网格点

根据面积权重分配原则，4个网格点的电荷密度为

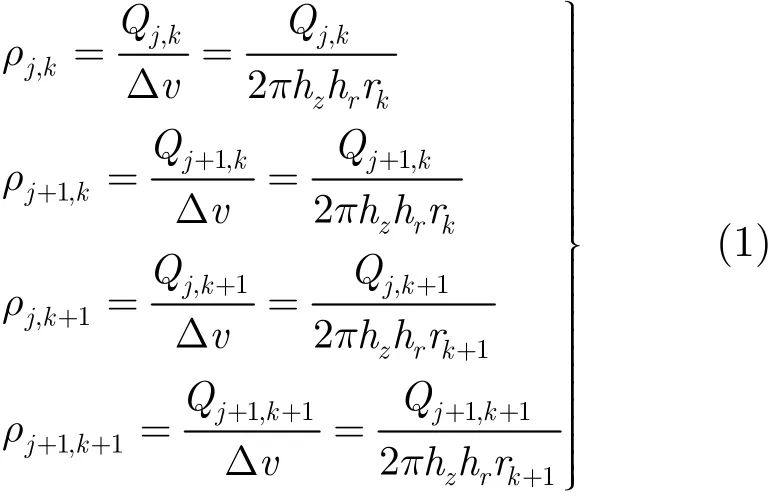
在经过一个时间步长dt以后，宏粒子由初始位置A(xn)运动到了终点位置B(xn*)，位移为AB(如图2所示)，下面仅讨论该宏粒子位移处于一个网格之内的情形(该宏粒子位移穿过多个网格的情形可以分开成多段采用叠加原理进行处理)。

另Δw=wn*−wn，=(wn*+wn)/2，根据式(1)的电荷分配原则和电流连续性方程∂Q/∂t+∫○J⋅dS=0，对于图2中节点1有ΔQj,k/Δt ++Ir,j,k+1/2=0，同理对于节点2、3和4可以列出类似的方程，联立求解这组方程可以获得相应网格边电流密度，

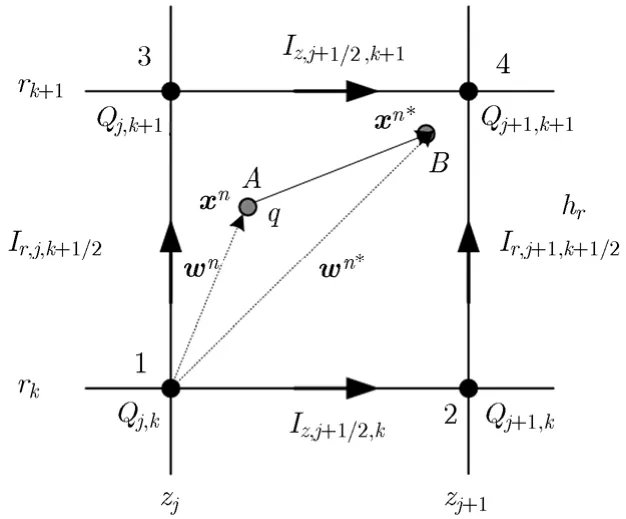
图2 PIC电流分配到网格各边

这样在每个时间步推进以后，都可以根据以上分析来确定空间各个网格点的电荷密度以及各网格边上的电流密度，从而为下一步利用FDTD方法来求解麦克斯韦方程组作好准备。

2.2 粒子注的空间电荷场

本粒子模型在一个时间步中的推进流程如图3所示：首先从右下角的方框开始，将电荷、电流分别加权分配于各网格点和各网格边，然后结合一定的边界条件采用时域有限差分算法来求解完整的麦克斯韦方程组，从而得到各个网格点的空间电荷场，即图3中的(Esc,Bsc)，再结合高频谐振腔场(Ecav,Bcav)得到施加于宏粒子的总电磁场，从而得到作用于宏粒子上的力，求解洛伦兹力方程，得到宏粒子新的速度与位置，接下来应用粒子在边界上的发射、吸收条件(某个边界作为粒子发射面使用，某个边界作为吸收边界使用，这些都可以在输入文件中定义)。随着时间步的推进，当一个高频周期T到来时，再根据Ramo定理来计算谐振腔新的间隙电压，一直迭代到所有的谐振腔间隙电压都达到稳定为止。

粒子注在漂移管空间所产生的电磁场即空间电荷场，程序中采用时域有限差分方法[7,8]求解Maxwell旋度方程来获得空间电荷场随时间的演化。整个求解过程是在圆柱形漂移管中进行的，忽略了具体谐振腔的形状，仅仅是一个漂移管模型，高频谐振腔对粒子注的影响将在后面讨论。

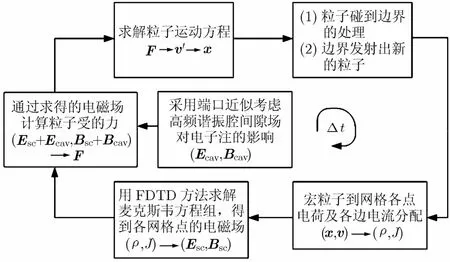
图3 粒子的推进流程

2.3 高频谐振腔场

速调管的高频谐振腔采用端口近似(portapproximation)来处理，如图4所示。

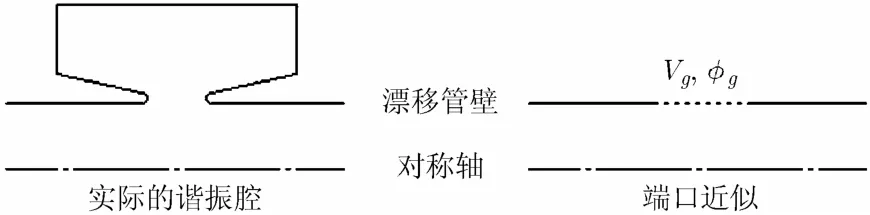
图4 端口近似的示意图

若已知谐振腔某模式(本程序中暂时先考虑TM010模)下的电磁场分布形式，如电场分布函数为fz(r, z)和fr(r, z)，磁场分布函数为fθ(r, z)，实际的谐振腔间隙电磁场值可以由谐振腔的间隙电压求得。本程序中的场形分布函数可以采用解析场和数值场两种形式来表征。解析场是根据谐振腔的特征结构参数由双曲余弦级数求和表示，这样得出来的谐振腔间隙场形与实际情形比较接近。数值场是先根据谐振腔的几何参数利用第3方软件，如CST微波工作室或Superfish来计算出谐振腔的谐振频率，R/Q，Q值，以及场形分布函数，而具体网格点的电、磁场值再通过插值方法来得到。

运动粒子经过谐振腔时将会在谐振腔中激起感应电流，如果间隙之间的距离远小于电子波长，此时可以略去滞后效应，从能量守恒的观点出发可以导出感应电流定律(Ramo’s theorem)[9]如下：

其中iind(t)为谐振腔间隙的感应电流，Vgap(t)为间隙电压，这里的Vgap(t)为纵向电场Ez沿谐振腔轴线的积分，即在式(3)右边的积分符号内，J(r,t)为电子注的运动电流，Ecav(r,t)为谐振腔间隙电场，二者都是与位置r有关的矢量。

根据等效电路模型有

其中in为感应电流的第n次谐波分量，Zn为第n次谐波腔的间隙阻抗QL为谐振腔的有载品质因数，fr为谐振腔的谐振频率)，若为基波腔则取n=1，若为2次谐波腔则取n=2。

综上，先在每个时间步中计算各谐振腔的感应电流，当一个高频周期结束后再将该周期内的感应电流作傅里叶分解以得到其基波分量和高次谐波分量，再通过式(4)求得新的间隙电压，直至各腔间隙电压达到稳定值为止。

2.4 粒子的推进

粒子的推进采用Boris[10]旋动格式实现，粒子的推进包括粒子的速度和位置推进，在Particle-In-Cell 算法中我们采用中心时间差分，粒子位置的更新是从(n−1)Δt到nΔt，粒子速度的更新是从(n−1/2)Δt 到(n+1/2)Δt ，粒子的位置和速度的更新是相差半个时间步长的，这即是传统的蛙跳算法。

考虑相对论效应，采用粒子的归一化动量u=γv，粒子的运动方程可写为

其中m，q，x，v分别为粒子质量、电量、位置和速度；γ为相对论因子；E，B对应于当前粒子位置处的电场强度与磁感应强度，通过插值就可以由网格点上记录的场值得到其它任意位置处的电磁场分量。

经过推导，粒子速度由时间步n−1/2的n−1/2u更新为n+1/2的n+1/2u推进流程为

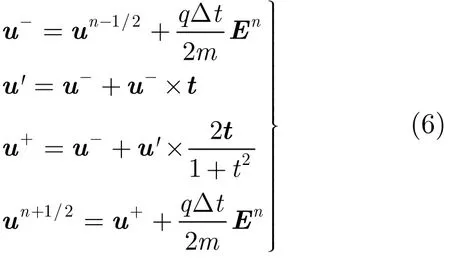
式中2t=t⋅ t。粒子的位置推进形式为

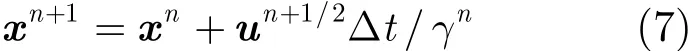
其中γn由u−根据来近似确定。

3 计算结果及相关讨论

下面给出以中国科学院电子学研究所研制的S波段50 MW高峰值功率速调管为算例的研究结果。该速调管应用于电子直线加速器，工作频率为2856 MHz，电子注直流电压为309 kV，电子注电流为376 A，采用均匀磁场聚焦。该速调管由6个谐振腔组成，采用单间隙输出腔，其余腔也均为单间隙谐振腔，输入腔与输出腔间隙中心间的距离为0.49 m。本程序计算时采用的输入功率为275 W(与实验时一致)，下面给出计算结果并对其进行分析讨论。

图5为最后一个时间步漂移管中的宏粒子分布，由于计算的需要本文给模拟区域加了一段必要的过渡段，即输入腔的间隙中心的z轴位置为0.08 m，各间隙中心间的距离均保持不变，纵轴r为宏粒子的径向位置对漂移管半径R0的归一化值，宏粒子是从发射面随机发射出来的。从图5中可以看到，在末前腔和输出腔出现了明显的电子注群聚块，有很强的密度调制。

图6表示在最后一个时间步漂移管空间中宏粒子归一化轴向动量γβz=γvz/c 随轴向距离z的分布，可知在输出腔(其间隙中心对应图6中的0.57 m处)中大部分电子由于受到间隙电场的减速作用，电子速度锐减，同时实现了从电子动能到微波能量的转移。

图7为在最后一个时间步漂移管空间中宏粒子归一化径向动量γβr=γvr/c 随轴向距离z的分布。随着运动距离的增加，宏粒子径向动量的零散也就越大，特别是到了输出腔的位置，由于有很强的径向电场作用，宏粒子的径向速度波动很大。

图8为宏粒子的相轨迹，它反映了宏粒子在依次受到各个谐振腔的调制而逐渐出现群聚的整个变化过程，它可以作为速调管结构及各项参数选择是否合理的重要参考之一。从图8中可以很明显地看出，在该参数结构下宏粒子出现了比较理想的群聚。

图9为电子注归一化运动电流的前4次谐波分量随轴向距离z的变化曲线，随着轴向距离的增大，电子注的群聚就越明显，运动电流的幅值也就越大，其中基波分量幅值最大，其大小也决定了速调管效率的高低，二阶及以上的谐波分量相对较小。

图10为同一工作电压(309.0 kV)下由KLY2D，LSP以及KLY6程序计算出的传输特性曲线，可见KLY2D与KLY6的差异比较大，由后者求出的最大输出功率高于前者的计算结果，而且可以注意到随着输入功率的增加KLY6程序预测的输出功率很快就达到了饱和，其原因是1维模型中电子动量都集中在轴向，高估了速调管中的互作用效率，而由KLY2D计算得到的输出功率变化要相对平缓很多。从图10中还可以看出，相同输入功率下KLY2D的计算结果要略低于LSP的结果，其原因为输出腔中电子注在轴向和径向都会出现严重的超越和交叉，LSP圆环模型所依赖的层流性假设不再成立，而KLY2D则不存在这一问题。

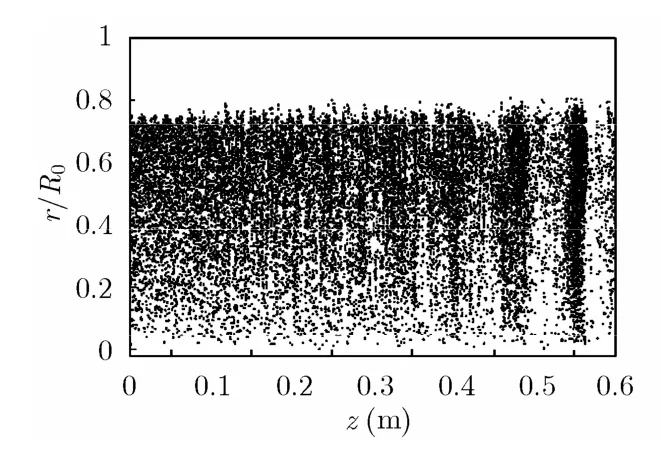
图5 r-z平面宏粒子的分布

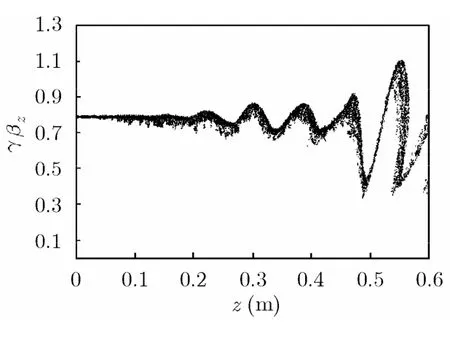
图6 宏粒子的轴向动量随运动距离z的变化

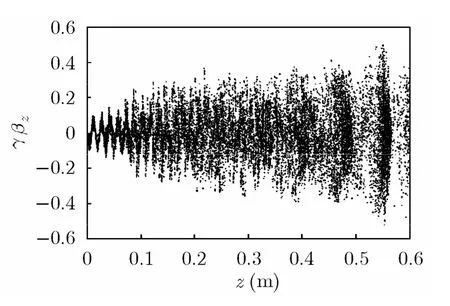
图7 宏粒子的径向动量随运动距离z的变化

图8 宏粒子的相轨迹

图9 电子注归一化运动电流的谐波分量随运动距离z的变化

图10 由KLY2D、LSP和KLY6计算的传输特性曲线

当输入功率为275 W时，由程序计算得到的输出功率为51.5 MW，效率为44.3%，而对应样管实验测得的输出功率为50.9 MW，由此可见，误差是很小的。

4 结束语

本文所介绍的粒子模型首次将粒子模拟思想与等效电路端口近似相结合。与1维模型相比，它考虑了宏粒子的径向运动，模拟了大量的宏粒子的运动，这样更接近真实的物理情形。采用端口近似方法，能够准确地模拟谐振腔高频场对注波互作用系统的影响，同时比全数值的3D模型节约运算资源。基于该模型我们开发出了国内首个速调管专用粒子模拟程序KLY2D。其运算时间与通常的粒子模拟程序相比大为缩短，从而极大地提高了数值模拟的效率。此外，本文的2.5D模型又是一个时域的粒子模型，能够记录下所有粒子的瞬态信息，可以模拟互作用系统随时间的演化过程，从而有助于分析谐振腔间隙电压从开始建立至达到稳定的复杂过程，这是传统的频域代码无法与之相比的。KLY2D运行稳定，计算结果可信度高，与本单位研发的实际管型实验数据进行对比验证，结果表明程序与实测值吻合得很好。

此模型还有很多需要完善的地方，接下来我们将考虑注波互作用区域入口处电子注的速度零散，使其更接近真实的物理情形。同时，我们将引入群聚腔为双间隙耦合腔的模型，使其能够用于扩展互作用速调管的模拟。

[1] Shintake T. Klystron simulation and design using the Field Charge Interaction (FCI) code[J]. Nuclear Instruments and Methods in Physics Research, 1995, Section A(363): 83-89.

[2] 赵鼎. 速调管非线性注波互作用程序的研究[D]. [博士论文],中国科学院电子学研究所，2007.Zhao D. Research on nonlinear beam-wave interaction program for klystrons[D]. [Ph.D.dissertation], Institute of Electronics, Chinese Academic of Sciences, 2007.

[3] Chernyavskiy I A, Cooke S J, and Vlasov A N, et al.. Parallel simulation of independent beam-tunnels in multiple-beam klystrons using TESLA[J]. IEEE Transactions on Plasma Science, 2008, 36(3): 670-681.

[4] Goplen B, Ludeking L, and Smithe D, et al..User-configurable MAGIC for electromagnetic PIC calculations[J]. Computer Physics Communications, 1995,87(1-2): 54-86.

[5] 邹峰, 薛谦忠, 刘濮鲲. 大回旋电子注双磁会切电子枪的数值模拟[J]. 电子与信息学报, 2008, 30(9): 2276-2278.Zou F, Xue Q Z, and Liu P K. Numerical simulation of large orbit gyrotron electron beam double CUSP gun[J]. Journal of Electronics & Information Technology, 2008, 30(9):2276-2278.

[6] Verboncoeur J P, Landon A B, and Glad N T. An object-oriented electromagnetic PIC code[J]. Computer Physics Communications, 1995, (87): 199-211.

[7] Huang Z Y and Pan G W. Universally applicable uniaxial perfect matched layer formulation for explicit and implicit finite difference time domain algorithms[J]. IEEE Transaction on Microwaves, Antennas & Propagation, 2008,2(7): 668-676.

[8] Wu D G, Chen J, and Liu C R. An efficient FDTD method for axially symmetric LWD environments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(6):1652-1656.

[9] 丁耀根. 大功率速调管的理论与计算模拟[M]. 北京：国防工业出版社, 2008: 33-43.Ding Y G. Theory and Computer Simulation of High Power Klystron[M]. Beijing: National Defense Industry Press, 2008:33-43.

[10] Birdsall C K and Langdon A B. Plasma Physics Via Computer Simulation[M]. Bristol: Adam Hilger, 1991: 58-63.