格上基于盆景树模型的环签名

王凤和 胡予濮 王春晓

①(西安电子科技大学计算机网络与信息安全教育部重点实验室 西安 710071)

②(泰山学院数学与系统科学学院 泰安 271021)③(山东建筑大学理学院 济南 250101)

1 引言

2001年，Rivest, Shamir 和Tauman[1]提出了环签名的概念。环签名允许成员完全匿名地实现签名，验证者可以验证该签名来自群组的成员，但无法确定签名者的身份。环签名提出后引起了广泛关注，提出了各种基于数论假设或者利用双线性对设计的标准环签名方案[2−5]及其变形的环签名方案如可控环签名[6]，代理环签名[7,8]等。环签名及其变形方案可以被广泛的应用于电子选举、电子现金、Ad hoc groups的匿名身份(认证)等领域。然而已有工作说明著名的大整数分解与离散对数问题在量子计算机上都可以在多项式时间内解决[9]，从而使得基于它们设计的密码系统在量子环境下都将不再安全。因此设计在后量子时代依然确保安全的环签名方案成为环签名领域一个有意义的研究方向。

格上的困难问题具有在量子计算环境下依然安全的特点，因此基于格设计密码算法具有后量子安全的优势。格上设计的密码系统除具有量子安全的特点之外还有其他的优点，例如格上算法的结构简单，运算快捷(主要使用模乘和模加运算而且仅仅涉及小整数运算)、格上困难问题在最坏和一般状态下的困难性等价等等。近几年来，越来越多的密码学家开始关注在一般格上设计可证明安全的密码系统，取得一系列的重要成果[10−16]。但与利用大数分解、离散对数设计的大量带有特殊安全性能的方案、协议比较，基于一般格建立的密码系统才刚刚起步，在格上设计的具有特殊功能的密码系统还很少，尤其注意到还没有在格上实现环签名的设计(尽笔者所知)。因此基于格设计环签名方案作为格理论在环签名领域中的有效应用也成为格基密码一个有价值的研究课题。

2009年E-Print上公开Peikert[13]的最新研究成果，Peikert在格上利用格和基的扩充技术和原象抽样函数[16]在盆景树模型(Bonsai Trees)下设计了一个标准模型下的数字签名方案和一个分级身份加密方案，其核心工作是盆景树模型下的格扩充技术，即从一个母格及其一组小的基向量(好基或小基)出发构造更高维数的格和它上面的小基。本文利用盆景树签名构造了一个格上的环签名方案。本文的环签名方案中每一位环成员掌握着一个格矩阵作为公钥，对应格上的一组小基作为成员的签名密钥。在每次签名时，签名者以自己公钥对应的格作为盆景树的根节点(母格)利用其他成员的公开钥和签名消息将自己的格扩展，得到一个更大维数的格并以此格作为盆景树的下一级节点(子格)，建立一个盆景树模型，在此过程中同时把母格上的小基扩展得到子格上的一组小基。利用子格上的小基通过盆景树签名完成自己的环签名。方案的安全性分析中说明方案允许成员实现完全匿名签名，验证者可以验证签名的合法性，并判断签名者确实来自群组，但是任何人不能发现签名者的身份。在标准模型下，证明方案的安全性是基于格上SIS问题的困难性。而格上SIS问题是量子计算环境下的困难问题，所以我们的格基环签名具有量子安全的特性。

2 基础知识

2.1 格

设v1, v2,…,vn是Rn上一组线性无关的向量，格Λ定义为所有这些向量的整数线性组合构成的集合，即构成格Λ的一组基。设ω是一个向量，将定义为向量ω的lp-范数，当p=2时，称作欧几里得范数。

2.2 格上的几个困难问题

以SVP和CVP问题为核心的格上困难问题，是格基密码安全性的保障，SVP和CVP存在很多近似问题，本节仅仅介绍本文相关的SVP和CVP和其近似问题-SIS问题。

(1)SVP问题 设A是格的一组基，SVP问题就是在格上寻找一个非零向量u满足任意格上的向量v,有||u||≤||v||成立。其中||⋅||为给定的范数。

(2)CVP问题 设A是格的一组基，ω是一个向量，CVP问题就是要在格上寻找u，使得任意格上的向量v有：||u−ω||≤||v−ω||。其中||⋅||为给定的范数。

(3)SIS问题(小整数解问题)参数q(⋅),m(n),β(⋅),给定n和寻找一个非零向量e，满足：Ae=0modq(n),||e||≤β(n)。

2.3 盆景树原理

Peikert引入的盆景树模型事实上是一个分级陷门函数，在盆景树模型下以某个格(一组基)作为根节点可以生成一个更大维数的格作为下一级的枝节点，同时得到格的一组基。这种由“根”到“枝”的“生长”可以是无陷门的即无指导生长(undirected growth)，此时“盆景师”在分级过程中没有使用陷门因此没有任何特权；也可以是有陷门时由“盆景师”控制盆景树的“生长”过程，包括控制生长(controlled growth)、扩展控制(extending control)和随机控制(randoming control)。本文主要使用盆景树的扩展控制方法，细节及其他原理参照文献[13]。格上的扩展控制(extending control)算法是一个由较小维数的格和基向量构造更大维数的格和基向量的算法。设任意一个格Λ(A)以及它的一组基S，由(A,S)得到一个更大维数的格Λ(A′)=Λ(A||)及其基向量S′。我们将扩展控制记为ExBasis(S, A′=A||)，算法描述如下：

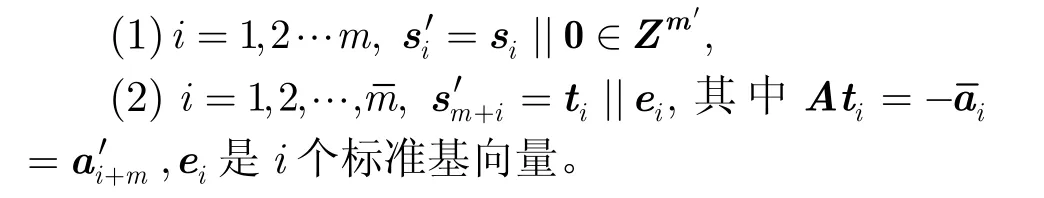
文献[13]说明在盆景树模型下可以利用上述扩展控制算法构造盆景树签名。

2.4 盆景树签名

本节简要介绍文献[13]给出的盆景树签名方案。

注：签名的各个参数都是n的函数。

2.4.2 签名 设签名消息M的hash值为μ∈(0,1)，根据μ各个位置的值选择对应公钥∈，令：=A||||||||…∈，利用扩展控制算法[13]得到格Aμ上的一组小基，进而利用原象抽样函数[16]生成格Aμ上的一个小向量：v=Sample D(Exbasis(S, Aμ),s)。如果取样得到0向量或者||v||≥s，则重新取样。向量v作为消息M的签名。

2.4.3 验证 首先计算消息M的hash值μ∈(0,1)，根据μ各个位置的值选择对应公钥∈，并与签名者的公钥级联得到矩阵=A||||||||…∈，然后验证：(1)v≠0，||v||≤s;(2)Aμv=0。通过则接受签名，否则拒绝签名。

3 本文提出的环签名方案

3.1 系统生成

n为整个方案的安全参数，其他参数都是n的函数。设U1…Ul是l个用户分别掌握一个格矩阵，以及对应格上的一组小基Si。密钥分配中心随机、独立地生成2k个矩阵∈，j=1,2,…,k，e=0或1。同时密钥分配中心也要将环成员的公钥级联成一个新的矩阵=1AA||A2||A3||…||Al−1||Al。设h(⋅):{0,1}*→{0,1}k为一个输出为k-bit的安全hash函数。则环公钥为(, A)，j=1,2,…,k，e=0或1，对应格上的Si作为用户Ui的签名密钥。其它安全参数定义为：m1=O(n⋅logn)，m2=O(n⋅logn)，m′=lm1+km2，

3.2 签名

设用户Ui要生成签名消息M的签名，消息的hash值μ=h(M)∈(0,1)k。Ui首先利用对应μ∈(0,1)k的各个分值选择公开参数矩阵，然后建立盆景树：利用秘密钥Si将格iA扩展为更大维数的格，并生成此格上的一组小基′。然后用户Ui改变′A中各个子阵iA的位置使之与环公钥A一致并相应得改变基中各分量的位置，得到Aμ和Sμ。通过Aμ,Sμ，利用盆景树签名得到向量v：v=SampleD(Exbasis(Si, Aμ),s)。v作为消息M的签名。

3.3 验证

验证者得到消息M的签名v后，首先计算hash函数值μ=h(M)∈(0,1)k，利用μ的各个分量值选取环参数矩阵，并与环公钥A级联得到Aμ，然后验证：(1)v≠0，||v||≤s; (2)Aμv=0。通过以上验证则接受签名，否则拒绝签名。

说明 该环签名的主要基于盆景树签名格完成签名，完备性验证参照文献[13]，本文略。

4 环签名的性能分析

4.1 匿名性

定理1 本文的方案实现了签名者身份的完全匿名性。

证明 消息的环签名是大维数格上的一个范数较小的向量，而大维数格矩阵Aμ中子阵A包含所有环成员的公钥信息，注意到这些公钥的位置是完全平等的，因此从任何一个成员的公钥出发都可能得到该消息的签名v，即每一个成员都可能生成此签名，因此验证者不能从v中分解出签名者公钥的任何信息，他只能以1/l的概率推测签名人的身份，l是成员的个数；而要通过大维数格上的一个小向量得到小维数格上的一组小基(签名密钥)来对应签名人的身份更是不可行的。进一步地，消息的环签名v服从格上的正态分布[13]，因此任意两个环成员的签名或者一个环成员对两个消息的签名服从的概率分布对验证者而言是不可区分的。所以环签名实现了无条件匿名性。 证毕

4.2 存在性不可伪造性

定义1 存在性不可伪造：一个签名方案称作是存在性不可伪造的，如果对于任意多项式时间的伪造者在掌握签名公钥的条件下通过与签名者的多项式有限次的交互得到有限个消息对应的签名，如果伪造者能够输出一个新消息的合法签名的概率是可以忽略的。

定理2 假设存在不是任何环成员的概率多项式时间敌手F能够至多通过Q次hash询问，Q1次环签名询问以不可忽略的概率ε伪造新的消息μ(假设μ是一个hash值)的合法环签名，其中消息μ从未在签名询问中被询问过。则可以构造算法S以近似ε/kQ1的概率来解大维数格上的SIS问题。

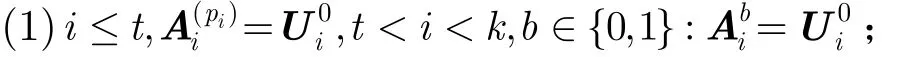
将矩阵A0作为环签名方案中环成员公钥级联得到矩阵，矩阵对应一个环签名方案中的环公开参数矩阵。以(A0,)来初始化敌手F，让敌手F来攻击以上环签名。

签名询问：设算法S开始为敌手F发送消息μJ的签名询问生成环签名：在列表L2中寻找此消息的签名记录vJ，若找到此消息则返回列表中相应的vJ作为签名。若消息μJ不在L2中，设i为第一个满足≠p的位置，算法S通过格及其好基S利ii用盆景树下的扩展控制算法得到格AμJ=A0||||||…||||及其好基S，然后μJ利用原象抽样算法得到消息μJ的签名vJ，将消息μJ的签名vJ发送给敌手F，同时在列表L2中存储消息μJ及其签名vJ。 在敌手F对所有签名询问满意后，敌手F以概率ε生成第Q1+1个消息μQ1+1的伪造签名vQ+1。算法S检查p是否是消息μQ+1的前缀，如果不是μQ1+1的前缀，算法S终止游戏，宣布失败。否则p是μQ1+1的前缀，则矩阵AμQ+1是由矩阵A0和k个Ui(b)级联得到。所以算法S可以通过添加子阵并调整子阵的顺序同时在vQ1+1上添加相应的0并调整顺序，得到一个向量v，满足：Av=0(modq),由模拟过程知||v||≤s。从而算法S成功得到Ax=0的一个小整数解。

分析算法S成功的优势：算法S成功的关键是随机选取的集合T中的比特串p应该是第Q1+1个消息μQ1+1的前缀，此概率接近1/kQ1,从而算法S成功的概率近似为ε/kQ1。 证毕

4.3 效率分析

方案的一个不足之处是在签名时要将盆景树模型下的母格扩充为一个比原始盆景树签名更大维数的格，原因是环成员需要联合其他成员的公钥。这使得环签名中签名格的维数要大于原始的盆景树签名。设m1=c1nlgq,m2=c2nlg q ，其中c1,c2为常数，本文的方案中签名格矩阵的列数和签名长度为kc1nlgq+lc2nlg q ，l为环成员的个数。所以本文签名效率要低于盆景树签名，事实上一般的特殊签名的效率总要比原始签名要低。本文环签名方案中用户的密钥长度都为m1lgq，与盆景树签名相同。公钥长度为2km2nlgq+lm1nlg q ，其中l是环成员个数，k是hash函数的输出长度。由于方案设计中仅仅使用到了小整数的模加和模乘运算，所以计算效率较高。但是方案密钥长度较大，所以存储代价较高，这也是当前格基密码普遍存在的效率瓶颈。如何设计效率更高的格基环签名方案值得进一步研究。

5 结论

利用盆景树模型，借助盆景树签名，在格上构造了一个环签名方案。实现了环签名的完全匿名性和签名的存在性不可伪造性，在标准模型下证明方案的不可伪造性是基于格上SIS问题的困难性，因此方案具有在量子计算环境下依然安全的优点。

[1] Rivest R, Shamir A, and Tauman Y. How to leak a secret [C].AsiaCrypt2001. Berlin, Springer-Verlag, 2001, Vol. 2248:552-565.

[2] Zhang Fang-guo and Kim K. ID-based blind signature and ring signature from pairings[C]. ASIACRYPT 2002,Queenstown, New Zealand, 2002: 533-547.

[3] Chow S. M, Yiu S-M, and Hui L C K. Efficient identity based ring signature[C]. ACNS 2005, LNCS, 2005, Vol. 3531:499-512.

[4] Herranz J and S′aez G. New identity-based ring signature schemes[C]. ICICS2004, LNCS, 2004, Vol. 3269: 27-39.

[5] Dodis Y, Kiayias A, Nicolosi A, and Shoup V. Anonymous identification in Ad Hoc groups[C]. Eurocrypt’2004, LNCS,2004, Vol.3027: 609-626.

[6] Wei Gao, Wang Gui-lin, Wang Xue-li, and Xie Dong-qing.Controllable ring signatures[C]. WISA 2006, LNCS, 2007,Vol. 4298: 1-14.

[7] Li Jin, Chen Xiao-feng, Yuen Tsz-hon, and Wang Yan-ming.Proxy ring signature: formal definitions, efficient construction and new variant[C]. CIS2006, LNAI, 2007,Vol.4456: 545-555.

[8] 鲍皖苏, 隗云, 钟普查. 原始签名人匿名的代理环签名研究[J].电子与信息学报, 2009, 31(10): 2392-2396.Bao Wan-su, Wei Yun, and Zhong Pu-cha. Research on proxy ring signature with anonymity of the original signer. Journal of Electronics & Information Technology, 2009, 31(10):2392-2396.

[9] Shor P W. Polynomial-time algorithm for prime factorizeation and discrete logarithm on a quantum computer[J]. SIAM Journal on Computing, 1997, 26(5):1484-1509.

[10] Lyubashevsky V and Micciancio D. Asymptotically Efficient Lattice-Based Digital Signature[C]. TCC2008, LNCS, 2008,Vol. 4948: 37-54.

[11] Regev O. On Lattice, learning with errors, random linear codes, and cryptography[C]. STOC’05, Baltimore, MD 2005:84-93.

[12] Lyubashevsky V. Lattice-based identification schemes secure under active attacks[C]. PKC’ 2008, LNCS, 2008, Vol. 4939:162-179.

[13] Peikert C. Bonsai Trees [EB/OL]. http:// eprint.iacr.org/2009/359.

[14] Alwen J and Peikert C. Generating shorter bases for hard random lattices[C]. In STACS’2009, Freiburg-Germany, 2009:75-86.

[15] Micciancio D and Regev O. Worst-case to average-case reductions based on gaussian measures[J]. SIAM J.Compututer, 2007, 37(1): 267-302.

[16] Gentry C, Peikert C, and Vaikuntanathan V. Trapdoors for hard lattices and new cryptographic constructions[C].STOC’2008, Victoria, BC- Canada, 2008: 197-206.