时域卷积信号的交替最小二乘盲分离算法

张 华 冯大政 庞继勇

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(上海贝尔股份有限公司研究与创新中心 上海 201206)

1 引言

近二十年来，盲源分离在语音[1]、图像[2]、通信信号[3]处理等各个领域得到了广泛应用，成为信号处理领域的研究热点。其中，联合块对角化方法[4,5](Joint Block-Diagonalization, JBD)是解决卷积盲分离的有效途径。文献[4]改进并归纳了基于类雅克比旋转的正交JBD算法(记作Jacobi-JBD)。正交JBD算法需要对目标矩阵进行预白化处理以保证混叠矩阵为(酉)正交矩阵，这要求至少存在一个目标矩阵为正定矩阵，且噪声是独立同分布的。并且，正交JBD方法不能修正因白化处理而引入的额外误差。于是，文献[5]通过改进JZD算法[6]提出一种非正交JBD方法(记为ZJBD)，不再需要白化处理。然而，该类算法每次迭代只估计待定矩阵的一个子块，容易使得不同的子块落到同一个信号子空间里，从而产生奇异解。

针对以上问题，本文提出一种基于交替最小二乘的三因子分解算法(记作ALS-JBD)，联合估计待定矩阵的所有参数，实现非正交JBD，从而克服了ZJBD易于产生奇异解的缺点。相对于Jacobi-JBD和ZJBD，ALS-JBD算法具有分离性能好且对初始值不敏感的特点。

2 问题描述

2.1 信号模型

N个源信号sn(t)经过阶数为P的多径信道，由M个传感器接收，第m路传感器上的接收信号为

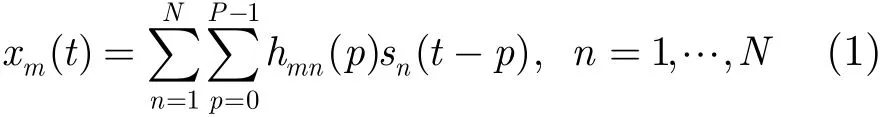
其中，hmn(p)表示第n个源信号到达第m个传感器的第p径信道响应。取窗长为W的接收滑窗，定义s(t)=[s(t),…,s(t−P−W +2)]T和x(t)=[x(t),… xmt −W +1)]T，构造s(t)=[(t),…,(t)]T和，则式(1)可表示为

其中混叠矩阵H可表示为

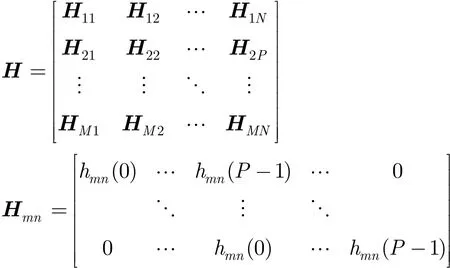
假设 (1)sn(t)零均值且相互独立；(2)H列满秩，即有MW＞N(P+W −1)。

2.2 接收信号相关矩阵的三因子乘积结构

令P表示广义Q-置换矩阵(其中Q=P+W−1)，考虑到盲分离所固有的尺度和排列不定性，将式(2)看作如下的等效模型并不会影响盲分离的效果，

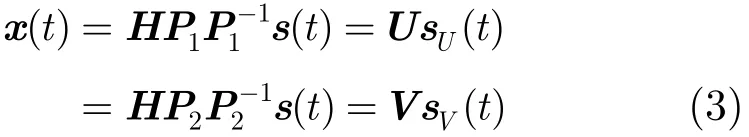
其中P1和P2均为广义Q-置换矩阵；sU(t)=s(t)=[(t),…,sT(t)]T，s(t)=s(t)=[(t),u(N)V …,(t)]T，下标 {u(1),…,u(N)}和{v(1),…,v(N)}为序列{1,…,N}的一个排列；U=HP1，V=HP2；令Δ=P，则有sU(t)=ΔPsV(t)。

当源信号满足假设(1)时，sU(t)与sV(t)的时延相关矩阵为

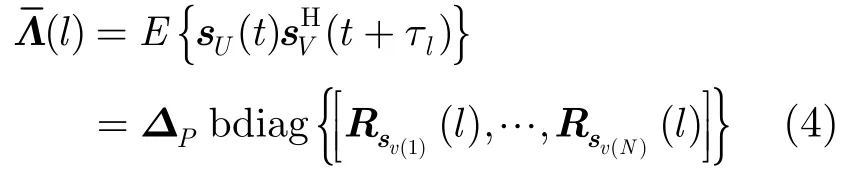
由式(3)和式(4)可知，接收信号的相关矩阵具有如下的三因子线性乘积形式

其中，矩阵U和V分别称为左、右混叠矩阵，其均是混叠矩阵H的Q-本质相等矩阵。

3 基于交替最小二乘的三因子分解方法

3.1 交替最小二乘方法

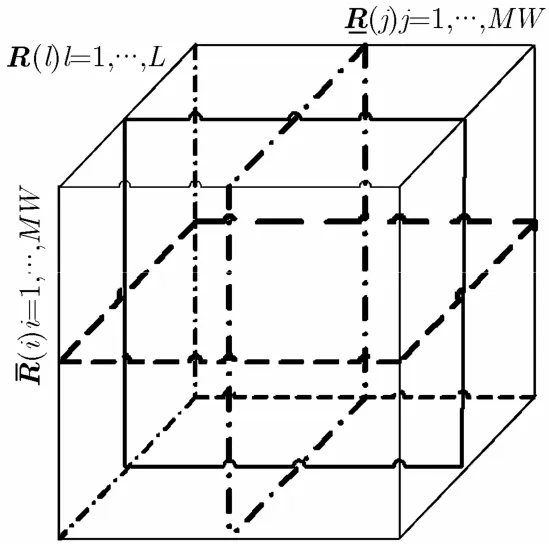
图1 3维矩阵切片示意图

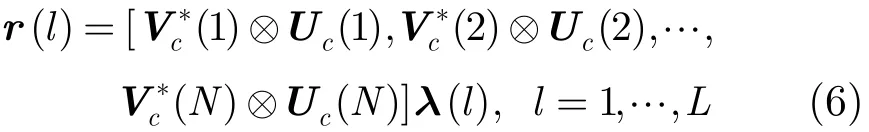
其中，⊗表示Kronecker乘积，V(n)∈ℂMW×Q和c Uc(n)∈ℂMW×Q分别表示矩阵V∈ℂMW×NQ和U∈ℂMW×NQ的第n个列块。令V∗°U=[(1)⊗U(1),c…,(N)⊗Uc(N)]，其中‘°’表示列块间Kronecker乘积。再令R1:L=[r(1),r(2),…,r(L)]，Λ1:L=[λ(1),λ(2),…,λ(L)]，则式(6)可简写成R1:L=(V∗°U)Λ。于是，若U和V已知，矩阵Λ的1:L1:L标准最小二乘解为Λ=(V∗°U)†R。从而，

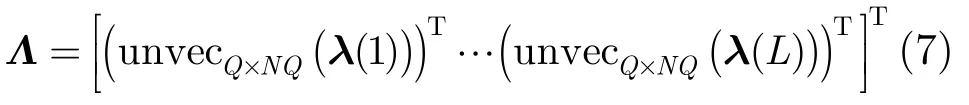
其中，符号unvecQ×NQ(⋅)表示将一个NQ2×1维的列向量按列重构成一个Q×NQ维的矩阵。

3.1.2 矩阵V的最小二乘解{R(j)∈ℂMW×L}可看作是3维矩阵ℜ在(1,3)维方向上的一组切片矩阵。则有

其中vr(j)表示矩阵V的第j行矢量；符号⊕表示列块Khatri-Rao积。再令1:MW=[(1),(2),…,(MW)]，式(8)所示矩阵组可简化表示为1:MW=(U⊕Λ)VH。类似地，若已知矩阵U和Λ，可得到矩阵V的标准最小二乘解

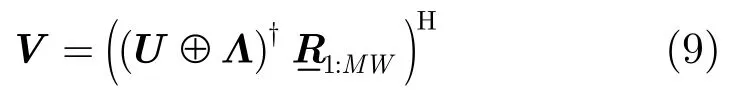
其中，ur(i)表示矩阵U的第i个行矢量；符号(⋅)˙T表示对分块矩阵的所有子矩阵进行转置运算。令式(10)所示矩阵组可表示为同样地，若已知矩阵V和Λ，则矩阵U的标准最小二乘解为

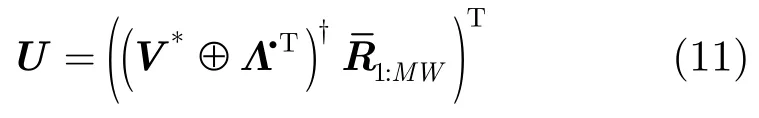
3.2 算法实现及其复杂度

选择任意MW×NQ维列满秩矩阵作为初始值，交替迭代估计待定矩阵Λ，V和U的最小二乘解，直到算法收敛，得到左、右混叠矩阵的估计U和V，即可从接收信号x(t)中分离出源信号。当MW=NQ并且目标矩阵个数L较大时，ALS-JBD算法单步迭代所需乘除运算次数近似为O(N4Q6)。

3.3 算法特点

ALS-JBD算法具有如下特点：(1)不需要预白化处理，消除了白化误差；(2)联合估计混叠矩阵的所有参数，避免了奇异解的出现；(3)最小二乘估计确保了算法的单调收敛性。

4 仿真实验

实验1 构造目标矩阵R(l)=HΛ(l)HH+ΔR(l)，定义无误差项和误差项的功率比值NER=10lg(||HΛ(l)HH/||ΔR(l))来衡量噪声扰动。采用与文献[5]中相同的全局拒噪水平GRL来评判算法的收敛性能，GRL越小说明算法性能越好。

设定参数M，W，N，Q和L分别为5，8，7，7和37，图2为经过100次Monte Carlo实验得到的GRL随NER变化的平均曲线。图3-图5分别给出在NER=5，10，15和20 (dB)时，3种算法在100次独立实验中的GRL随机值。由图2-图5可以明显看出，相比于类Jacobi-JBD[4]和ZJBD[5]方法，ALS-JBD算法具有最优且最稳定的收敛性能。

图2 GRL随NER变化曲线

图3 ALS-JBD算法的GRL数值

图4 ZJBD算法的GRL数值

图5 Jacobi-JBD算法的GRL数值

实验2 N=2段语音信号(图6(a))通过P=4径瑞利信道，由M=4个麦克风接收，得到图6(b)所示的接收信号(滑动窗长W=4)。图6(c)和6(d)分别为ALS-JBD和ZJBD得到的分离信号波形。表1采用(1)算法分离性能参数PI[1]；(2)巴克谱失真测度BSD[7]两个客观指标来对比两种算法得到的分离信号的相异度和谱失真度。由图6和表1不难看出，ALS-JBD算法具有更加有效的分离性能。

5 结论

本文分析指出卷积混叠接收信号的相关矩阵具有独特的三因子分解结构和可联合块对角化的特点。通过对目标矩阵组所有元素进行切片分割和排列规划，提出基于交替最小二乘的联合块对角化算法，交替迭代地估计左、右混叠矩阵和块对角矩阵的标准最小二乘解，进而分离出源信号。该算法无需白化处理，具有对初始值不敏感、估计精度高、收敛性能稳定和分离效果好的特点。

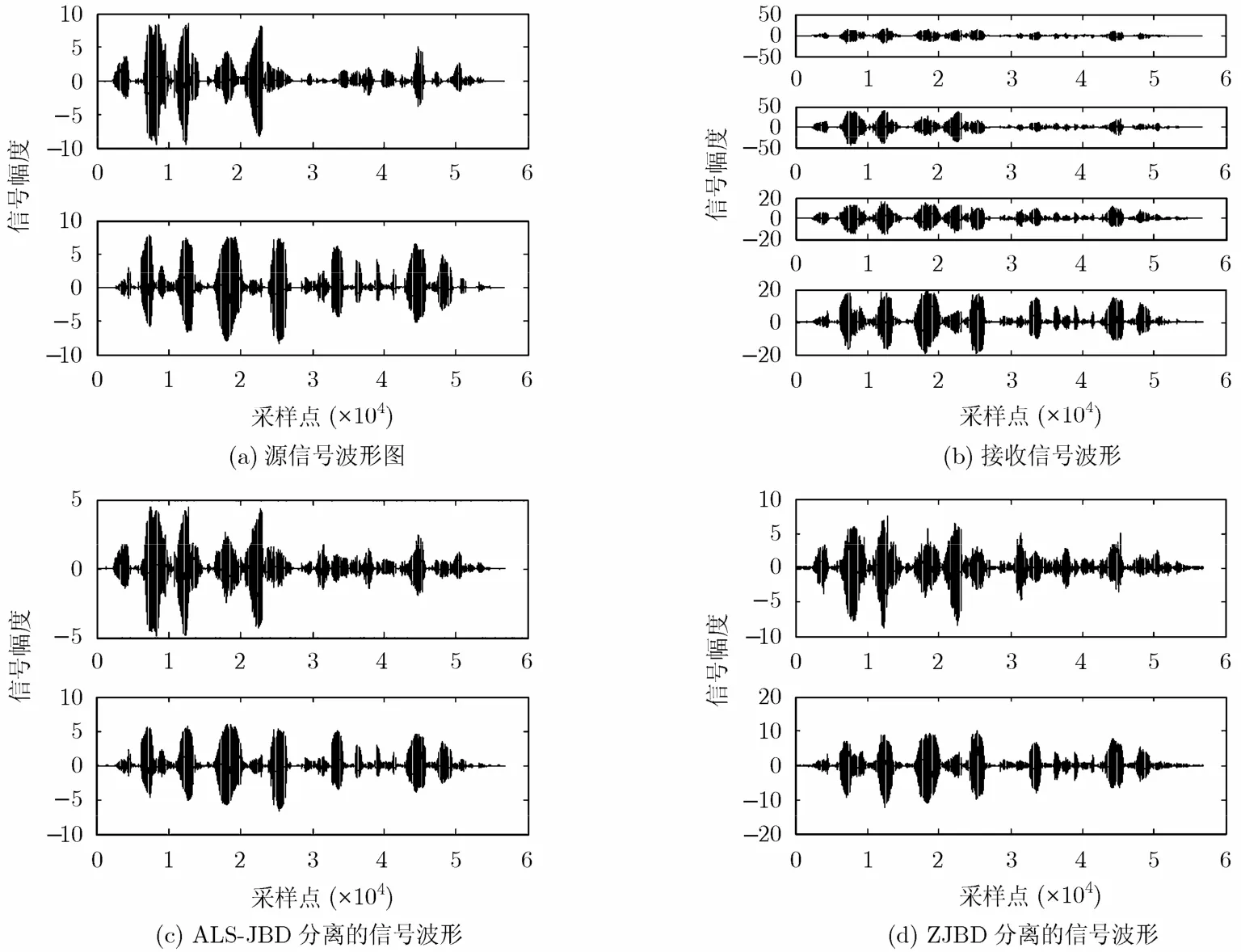
图6 源信号、接收信号和分离信号波形图

表1 分离性能测度

[1] 刘建强, 冯大政. 基于多信道信号增强的卷积混叠语音信号盲分离的后处理方法[J]. 电子学报, 2007, 35(2): 2389-2393.Liu Jian-qiang and Feng Da-zheng. Blind separation of convolutive speech mixtures with post-processing based on multichannel signal enhancement[J]. Acta Electronia Sinica,2007, 35(2): 2389-2393.

[2] 王睿, 方勇. 基于2-D共因子的精确提取的图像盲复原方法[J].电子与信息学报, 2009, 31(1): 108-111.Wang Rui and Fang Yong. Blind restoration of blurred image based on precise extraction of 2-D GCD[J]. Journal of Electronics & Information Technology, 2009, 31(1): 108-111.

[3] 付卫红, 杨小牛, 刘乃安, 曾兴雯. 基于子空间分解的多通道盲解卷积算法[J]. 电子与信息学报, 2009, 30(1): 25-30.Fu Wei-hong, Yang Xiao-niu, Liu Nai-an, and Zeng Xing-wen. Algorithm for multichannel blind deconvolution based on subspace decomposition[J]. Journal of Electronics &Information Technology, 2009, 30(1): 25-30.

[4] Abed-Meraim K and Beloucharni A. Algorithms for joint block diagonalization[C]. Proc. EUSIPCO’04, Vienna,Austria, Sept. 6-10, 2004: 209-212.

[5] Ghennioui H, Fadaili E M, and Moreau N T, et al.. A nonunitary joint block diagonalization algorithm for blind separation of convolutive mixtures of sources[J]. IEEE Signal Processing Letters, 2007, 14(11): 860-863.

[6] Fadaili E M, Thirion-Moreau N, and Moreau E.Non-orthogonal joint diagonalization/zeros-diagonalization for source separation based on time-frequency distributions[J].IEEE Transactions on Signal Processing, 2007, 55(5):1673-1687.

[7] 易克初, 田斌, 付强. 语音信号处理[M]. 北京：国防工业出版社, 2001: 146-147.