完全条件置换子群与有限群的超可解性

胡玉生， 张利英， 丁 华

（安徽财经大学统计与应用数学学院，安徽蚌埠 233030）

1 引 言

2005年，郭文彬[1]提出了完全条件置换子群的概念。按照文献[1]的术语称有限群G的子群H为G的完全条件置换子群，如果对于G的任意子群K，存在＜H，K＞的某个元素x，使得HKx=KxH。利用完全条件置换子群的概念，人们得到了一些非常有益的结果。例如，文献[1]中证明:如果有限群G的极小子群和4阶循环子群都在G中完全条件置换，则G超可解。

上述定理利用极小子群和4阶循环子群的完全条件置换性得到了有限群G超可解的结论，从这一角度出发，文中研究了有限群G的极小子群和4阶循环子群，得出:如果G的极小子群都包含在SE（G）中，且G的4阶循环子群在G中完全条件置换，则G为超可解群。

2 主要结果

首先给出下面的引理。

引理1[1]设G为有限群，H为G的子群，K为G的正规子群，则

1）如果H在G中完全条件置换，则HK/K在G/K中完全条件置换。

2）如果H在G中完全条件置换，则对于任意x∈G，Hx也在G中完全条件置换，其中，Hx= {hx=x-1hx|h∈H}是H的共轭子群。

3）如果T≤M≤G，T为G的完全条件置换子群，则T也为M的完全条件置换子群。

引理2[2]设G是内超可解群，则G有如下结构:

1）存在正规子群P∈Sylp（G），使G=P∝M，P/Φ（P）为G/Φ（P）非循环的极小正规子群;

2）如果p＞2，则exp（P）=p;若p=2，则exp（P）≤4，且p2||G|;

3）存在c∈P﹨Φ（P），使＜c＞不是G的正规子群;

4）如果P为Abel群，则Φ（P）=1;

5）P不是Abel群时，Φ（P）=Z（P）=P′;

6）G为Sylow塔群或G为内幂零群。

引理3[3]设G为内超可解群，P为G的正规Sylow p-子群，若有N＜|G，G/N超可解，则P∈Sylp（N）。

定理1 如果G的极小子群都包含在SE（G）中，且G的4阶循环子群在G中完全条件置换，则G为超可解群。

证明 假设定理不成立，而设G为极小阶反例，则

1）G为内超可解群。

事实上，对于任意K＜G，因为K的任一极小子群H≤SE（G）∩K≤SE（K），由引理1知K的4阶循环子群在G中完全条件置换，从而在K中完全条件置换，所以K满足定理条件。由G的极小性知，K超可解，故G为内超可解群。从而G具有引理2的结构，设P为G的正规Sylow p-子群。

2）如果exp（P）=p，由条件知P≤SE（G），从而由G/P超可解知G超可解，矛盾，所以，必有p =2。如果G有Sylow塔性质，则由p=2知G= P×M超可解，矛盾。故由引理2知G为2aqb阶的内幂零群。

3）任意a∈P﹨Φ（P），o（a）=4。

设＜x＞为G的Sylow q-子群，令

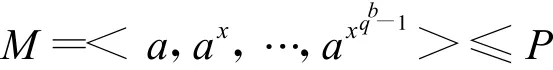
则

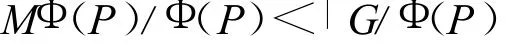
由P/Φ（P）的极小性知，P=MΦ（P）=M，因为＜axqi＞≤SE（G），1≤i≤b，所以，P≤SE（G），于是由G/P超可解知G超可解，矛盾。

4）导出矛盾。

因为G为内超可解群，故存在P∈Syl2（G），使P＜|G，P/Φ（P）是G/Φ（P）的极小正规子群，且P/Φ（P）非循环。设H为G的p-补，任取Hq∈Sylq（H），则Hq∈Sylq（G）。因为对于∀g∈P﹨Φ（P）有＜g＞在G中完全条件置换，所以存在y∈＜g，H＞使得

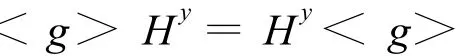
且

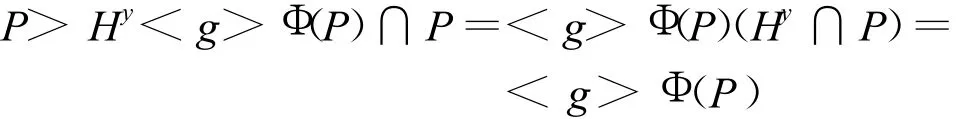
所以

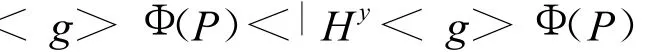
从而

又P/Φ（P）是Abel的，故

而

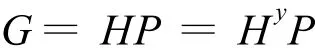
故

但

这与P/Φ（P）是G/Φ（P）的极小正规子群矛盾。故极小阶反例不存在，G为超可解群。

定理2 设N为G的正规子群使得G/N超可解，若N的极小子群皆属于SE（G），且4阶循环子群在G中完全条件置换，则G为超可解群。

证明 仿照定理1的证明及引理3得证。

[1] Guo Wenbin，Shum K P，Alexander Skiba.Conditionally permutable subgroups and supersolubility of finite groups[J].Southeast Asian Bulletin of Mathematics，2005，29:493-510.

[2] 陈重穆.内外∑-群与极小∑-群[M].重庆:西南师范大学出版社，1988:1-90.

[3] 王品超.有限群的C-正规子群[J].曲阜师范大学学报，1997，23（4）:5-7.

[4] 韦华全，谷伟平，黄杰山，等.子群的半覆盖-远离性与有限群的可解性[J].南昌大学学报:理科版，2009，33（3）:224-226.

[5] 郭鹏飞，郭秀云.弱s-置换性传递的有限群[J].纯粹数学与应用数学，2009，25（4）:649-653.

[6] 王丽芳.s-半置换子群对有限群的p-超可解性的影响[J].数学研究，2009，25（4）:434-440.