法锥条件下非凸非线性优化问题的同伦算法

赵雅玲， 申海明， 王秀玉

（长春工业大学基础科学学院，吉林长春 130012）

0 引 言

同伦算法是证明非线性问题解存在的有效方法之一[1-3]，文献[4-9]研究了非线性优化问题的组合同伦算法。文献[10]研究了含有较多约束的光滑非凸优化的凝聚同伦内点法;文献[11]研究了光滑非凸优化的动约束组合同伦算法，但上述文献所构造的同伦方程均为组合同伦，把组合同伦方程中的第二个方程改换为F-B函数，得到一个新的同伦方程，来研究非凸非线性优化问题。

文中首先介绍一些同伦的基础知识，然后给出主要结论，最后利用路径跟踪的方法得到互补问题的解。

下面介绍文中用到的非线性分析方面的一些定义和定理。

正则性定义:设φ:D⊂Rm→Rn是光滑映射，对任意y∈Rn，记φ-1（y）={x∈D|φ（x）=y}为y在映射 φ下的逆像。如果 φ在 x（0）∈D处的Jacobi矩阵∂φ（x（0））/∂x行满秩，则称x（0）是映射φ的正则点;否则，称 x（0）是φ的临界点。如果对所有的x（0）∈φ-1（y（0））都是映射 φ的正则点，则称y（0）是映射φ的正则值;否则，称y（0）是φ的临界值。

引理1（参数化的Sard定理） 设V⊂Rn，U⊂Rm均为开集，φ:V×U→Rp是Cr映射，这里r＞max{0，m-p}。如果0∈Rp是φ的一个正则值，那么对几乎所有a∈V，0是φ（a，◦）的一个正则值。

引理2（逆映像定理） 如果0是映射φ（a，◦）的正则值，那么逆映射φ-1（a，◦）由有限条一维光滑流形组成。

引理3（一维流形分类定理） 一维带边光滑流形的每个连通分支，或者微分同胚于单位圆周，或者微分同胚于区间（0，1]或（0，1）或[0，1]。

考虑如下问题（P）:

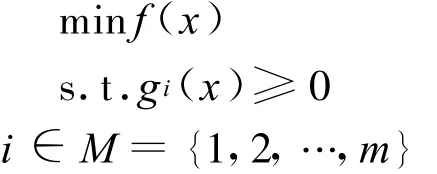
记

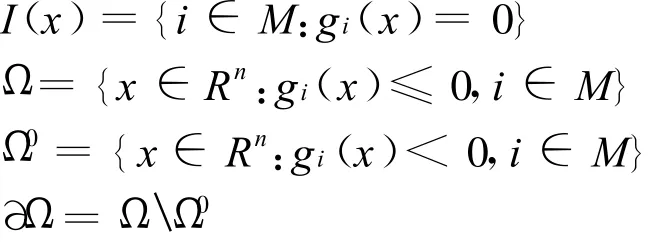
文中需要如下假设条件成立:

1）f，g∈Cr（r≥2）;

2）Ω0非空，Ω有界，连通;

3）∀x∈∂Ω，{▽gi（x）:i∈I（x）}正独立，即

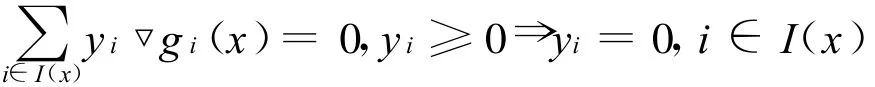
4）Ω满足法锥条件，即

1 主要结论

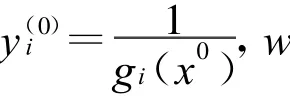
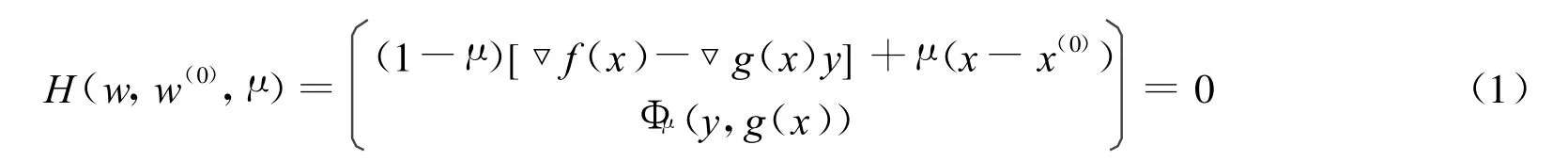
其中:

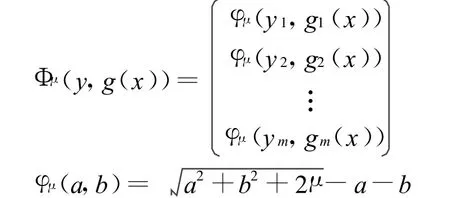
当μ=1时，式（1）为

及

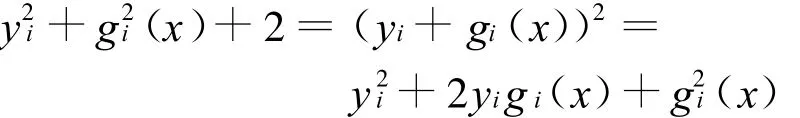
解得

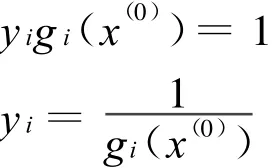
有唯一解。

当μ=0时，式（1）为:

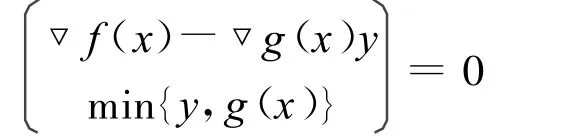
此为问题（P）的K-K-T方程。

显然有

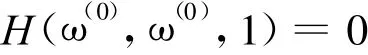
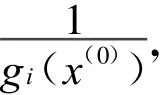
证明 H（ω，ω（0），μ）的Jocobi矩阵记为DH，

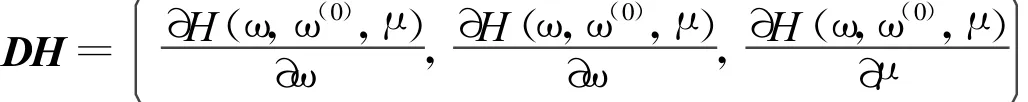
而

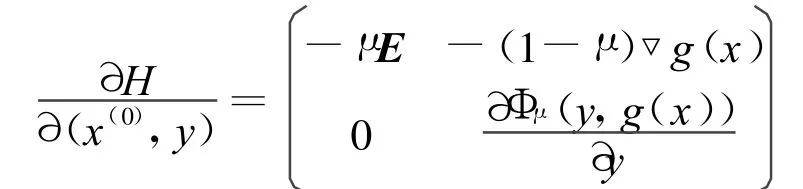
可逆，其中μ∈（0，1]，E为单位矩阵。

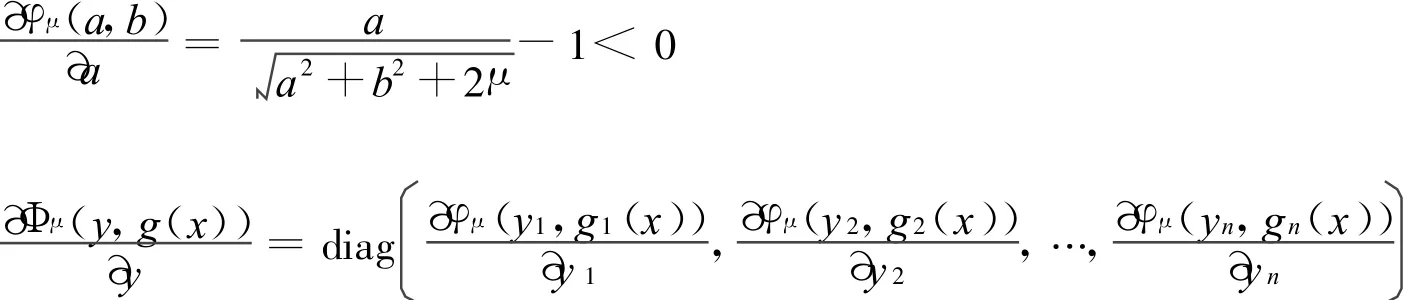
从而DH行满秩，由参数化的Sard定理知，0是H（ω，ω（0），μ）正则值。再由逆映像定理知，H-1（0）所含曲线是光滑的，且 H（ω（0），ω（0），1）= 0，因而，存在一条起始于（ω（0），1）的光滑曲线，记为。

证明 反证:若 Γω（0）无界，则存在（x（k），y（k），μk）∈Γω（0），且有‖（x（k），y（k），μk）‖→∞（k→∞），由同伦方程（1）的第二式得:

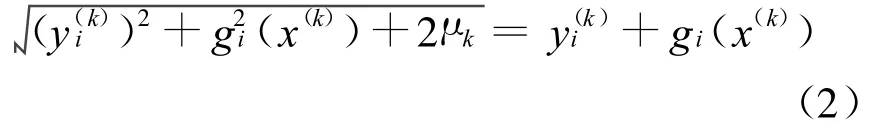
由式（2）得:

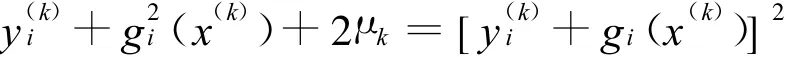
即

由式（2）和式（3）知:

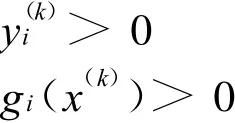
因而x（k）∈Ω，从而{x（k）}有界，记

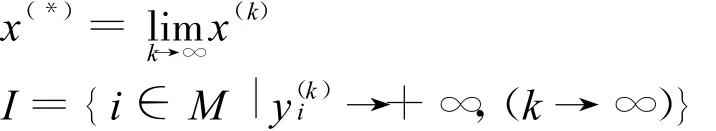
对某i，若y（k）i→+∞，必有gi（x（k））→0（由式（3））。因此，有I⊂I（x（*）），由同伦方程（1）的第一等式得:

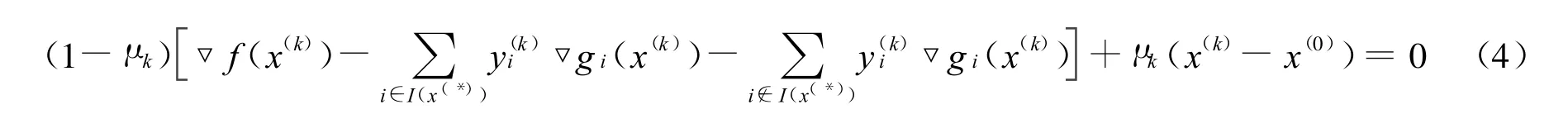
情形（1）:μk→μ*=1。

式（4）两边取极限得

此与4）矛盾。

情形（2）:μk→μ*∈[0，1）。

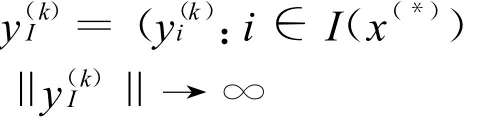
由式（4）得:

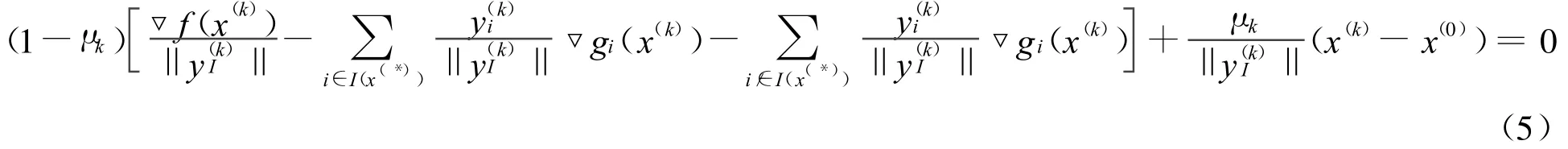
式（5）两边取极限得:

其中

此与3）矛盾。因此，Γω（0）是有界光滑曲线。

引理6 若假设1）～4）条件成立，同伦映射H由式（1）给出，则对几乎所有的x（0）∈Ω（0），，同伦方程（1）的零点集 H-1（0）包含一条起始于（ω（0），1）的光滑曲线 Γω（0）。当μ→0时，Γω（0）的极限点存在，记为（x（*），y（*），0），（x（*），y（*），0）为非凸非线性优化问题的K-K-T点。

证明:由引理4和引理5得Γω（0）的存在性及连续性。又由一维光滑流形的分类定理知:Γω（0）或微分同胚于单位圆周，或微分同胚于单位区间（0，1]。

注意到:

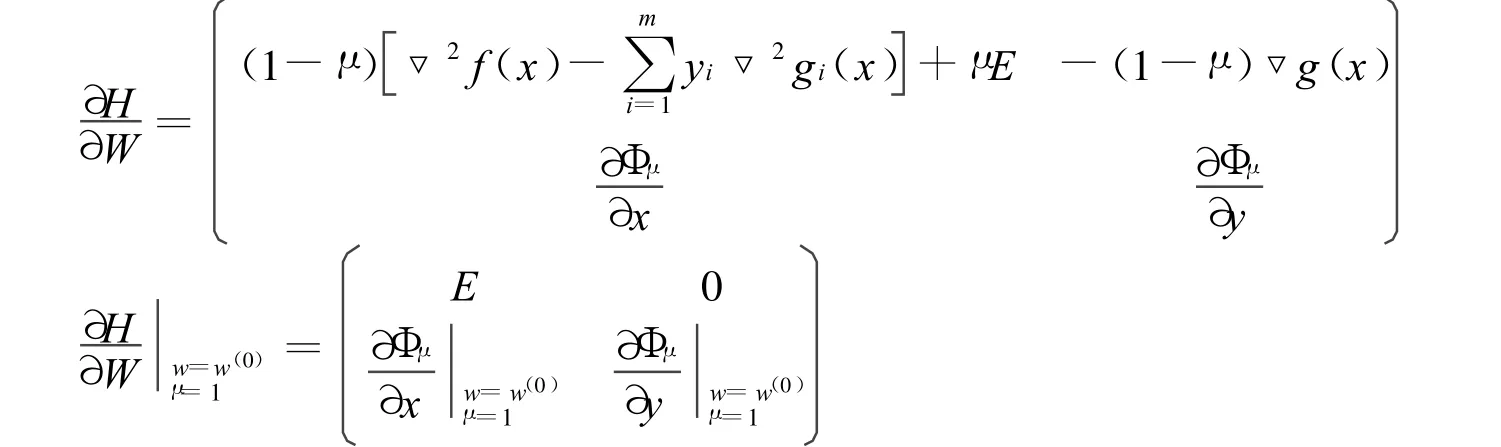
是非奇异矩阵，Γω（0）不能微分同胚于单位圆周，只能微分同胚于单位区间（0，1]。设（ω（*），μ*）为Γω（0）的极限点，则只有下列4种情况可能出现:

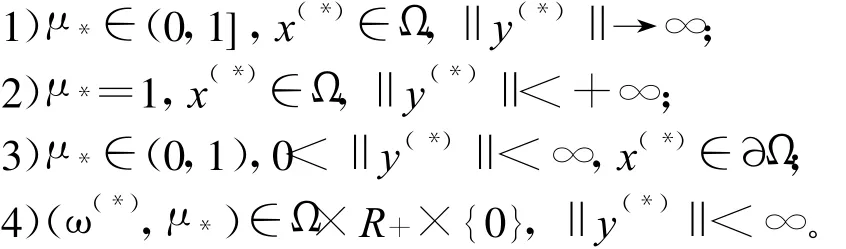
证明:由引理5知，情形（1）不可能出现;又由同伦方程H（ω（0），ω（0），1）=0在Ω（0）×R++×{1}有唯一解（ω（0），1）知，情形（2）不可能出现;由式（3），如果x（*）∈∂Ω，则有某y（*）i →∞，情形（3）也不可能出现;因而，只有情形（4）是唯一可以成立的结论。其余显然可证。

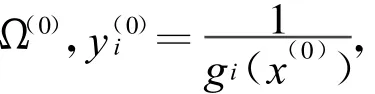
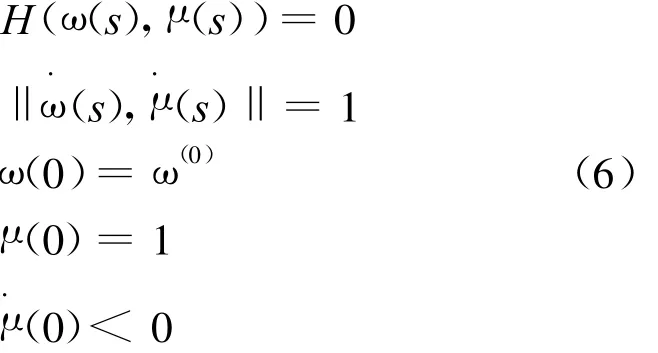
关于s微分式（6）的第一个等式，得到如下结论。

引理7 同伦方程H（ω，ω（0），μ）=0所确定的解曲线（ω（s），μ（s））满足如下微分方程的初值问题:

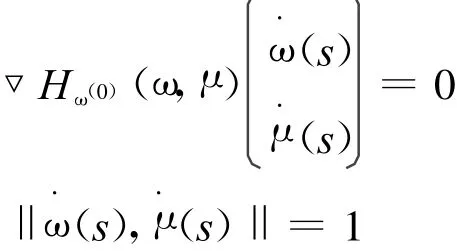
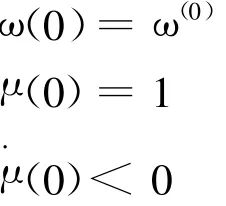
并且，若有s（*）＞0使得μ（s（*））=0，则x（*）=x（s（*）），y（*）=y（s（*））是非线性非凸优化问题的K-K-T点。

2 数值算例及算法

算法（Euler-New ton法）:

1）给定初始点v（0）=（ω（0），1）∈Rn+m×{1}和初始步长h＞0，校正误差tol＞0，终止误差μ*;

2）计算 H′（v（0））=H′的核空间的单位向量ζ∈Rn+m+1，并按如下方法选取切向量t（H′），计算

若式（7）的符号为（-1）m+1，则t（H′）=ζ。若（*）的符号为（-1）m，则t（H′）=-ζ，并置v= v0;

3）计算预估点u=v+ht（H′）;

4）计算dist=‖（H′（u））+H（u）‖;

5）计算校正点u=u-（H′（u））+H（u），它是解同伦方程H（u）=0的广义New ton法，其初始迭代点为预估点，这里（H′（u））+是H′（u）的广义逆;

6）若dist＜tol，则完成校正，转7），否则转4）;

7）若μ≤μ*（μ为u的最后一个分量），则终止。否则，选择新步长 h，并置 v=u，t= t（H′（u）），转3）。

例:minf（x）=（x1+4）2+（x2-2）2

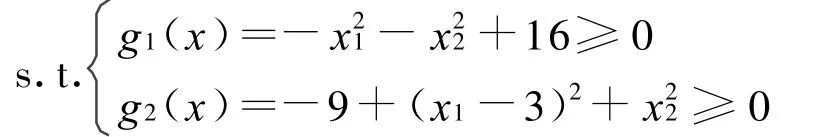
应用Matlab7.0编程计算结果见表1。

表1 编程计算结果

[1] Kellogg R B，Li T Y，Yorke J A.A constructive proof of the Brouwer fixed-point theorem and computational result[J].SIAM J.Numer.Anal.，1976，18:473-483.

[2] Smale S.A convergent process of price adjustment and global Newton method[J].J.Math.Econom.，1976，3:1-14.

[3] Chow S N，M allet-Paret J A.Finding zeros of maps:homotopy methods that are constructive with probability one[J].Math.Comput.，1978，32:887-899.

[4] Lin Z H，Li Y，Feng G C.A combined homotopy interior method for general nonlinear programming problem[J].Appl.Math.Comput.，1996，80:209-226.

[5] Lin Z H，Y Bo，Feng G C.A combined homotopy interior method for nonconvex programming[J]. Appl.Math.Comput.，1997，84:193-211.

[6] Feng G C，Lin Z H，Bo Y.Existence of Interior pathway to a Karush-Kuhn-Tucker point of a nonconvex programming problem[J].Nonlinear Analysis，Theory，MethodsApplications，1998，32（6）:761-768.

[7] Liu Q H，Yu B，Feng G C.An Interior point pathfolling method for nonconvex programming with quasi normal cone condition[J].Advances in Mathematics，2000，29（4）:381-382.

[8] Liu Q H，Yu B，Feng G C.A combined homotopy interior point method for nonconvex nonlinear programming problems under quasi normal cone condition（in chinese）[J].Acta.Math.Appl.Sinica.，2003，26:372-377.

[9] Yang Y，Lu X，Liu Q.A combined homotopy infeasible interior-point for convex nonlinear programming[J].Northeast Math.J.，2005，22（2）:188-192.

[10] Yu B，Feng G C，Zhang S L.The aggregate constraint homotopy method for nonconvex nonlinear programming[J].Nonlinear Anal.，TM A，2001，45:839-847.

[11] Yu B，Shang Y F.Boundary moving combined homotopy method for nonconvex nonlinear programming[J].Journal of Mathematical Research and Exposition，2006（4）:831-834.