基于视觉认知的全局优化算法

孙雅芳， 王晓丹， 徐俊彦， 刘庆怀

（长春工业大学应用数学研究所，吉林长春 130012）

0 引 言

近几年来，全局优化方法得到了快速的发展，尤其是智能优化算法中的禁忌搜索算法、模拟退火算法、神经网络算法、遗传算法、蚁群算法得到了广泛的研究与应用，但是还需进一步的完善与改进。

禁忌搜索算法[1-2]是模拟人类智能的全局优化算法，此算法具有较好的局部寻优能力，但会出现早熟现象。模拟退火算法[3]属于一种低级的智能，它模拟物体退火而形成的一种现代优化算法，其计算量虽然比Monte Carlo方法明显减少，但其全局收敛性仍很差。神经网络算法[4]是通过构造人工神经网络模型的一种智能算法。此算法计算快速简单，但此算法容易陷入局部最优解。遗传算法[5]是一种利用进化论中优胜劣汰、适者生存的原理而提出基于生物自身能力的智能算法。遗传算法是在整个空间内进行全局搜索，但其算法的计算时间长，经常会出现早熟收敛现象。蚁群算法是模仿蚂蚁依赖信息素进行通信而显示出的社会行为一种分布式智能模拟算法。此算法可以得到较好的全局最优解，有较强鲁棒特性，它是一无监督并行算法。此算法缺点是参数较多，而且没有确定的方法给出参数一个固定值，只能依靠实验或者是经验，计算时间较长，且容易出现死循环或者停止现象。了望算法[6]是基于通过了望确定群山最高点的常识提出的一种算法。在了望算法中主要包括了望管理机制、产生了望点策略、局部问题构造与求解。此算法是全局搜索，但易产生漏点现象。禁忌搜索算法、模拟退火算法、神经网络算法、遗传算法、蚁群算法、了望算法在解决全局优化问题会产生漏点的现象或者只是达到局部最优，由此提出基于视觉认知的全局优化算法。

文中给出了基于视觉认知的全局优化算法，确保在产生眺望点时，不存在漏点的现象，且用数学的方法证明了由算法产生的序列依概率收敛于全局最小值，通过数值例子对算法加以实现，并对全文进行了总结。

1 主要结果

1.1 基于视觉认知的全局优化算法

针对如下形式的全局优化问题

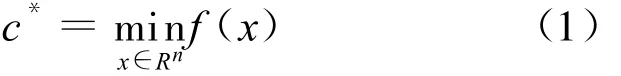
假设:

1）f:Rn→R连续，且有下界;

2）存在一个实数c0，使得水平集

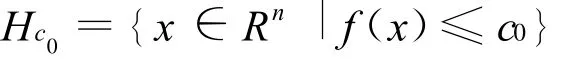
非空有界。

算法:

1）取ε＞0充分小，样本点数N∈Z+，令k= 0，c0=f（x0）。

3）产生眺望记忆机制。

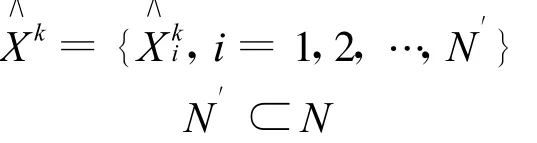
5）计算

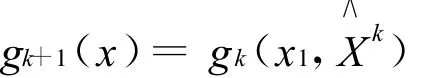
1.2 取样与更新

在算法中，起始密度选取为g0（x）=U（D），D⊂Rn为足够大的超立方体，其它步骤的取样密度选取以下核密度函数，即令

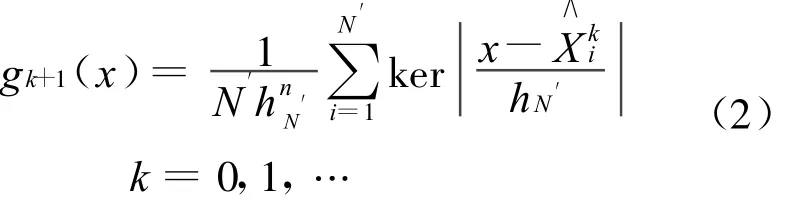
在这里，利用相对熵方法[7]来更新取样密度函数gk+1（x）。

为了简化计算，所选取的核函数为

式中:xj——向量x=（x1，x2，…，xn）的第 j个分量。

这样的核函数给取样和密度函数的更新带来了方便，结合式（2）与式（3），得到取样核密度函数为:

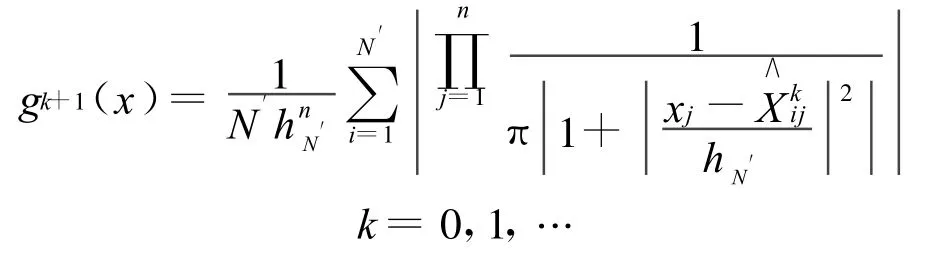
1.3 算法的收敛性

定理1 设{ck}是由算法产生的序列，存在c使

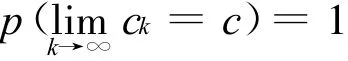
证明:由算法知

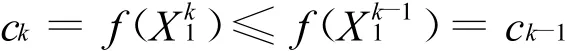
所以{ck}为单调下降序列。又因为由假设（1）知ck有界，则

证明 先证必要性:

再证充分性:

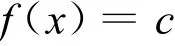
则∀x∈Rn，有

采用反正法证明:

根据算法

所以

即可知

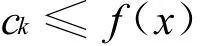
证明 由终止条件，当

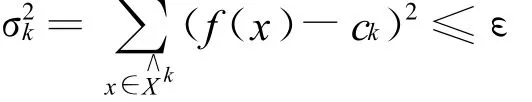
时，对∀ε，存在K，当k≥K时，有

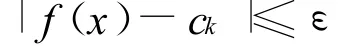
即可知对∀x∈Hc，有

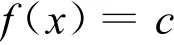
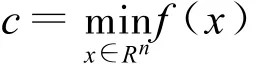
相应地Hc为最优点集。

2 数值算例[8]

所有的算法使用Matlab编程实现[9]，计算条件:CPU P4-1.0 GHz，256 M RAM，Matlab7.0。

例1 Rosenbrock函数:

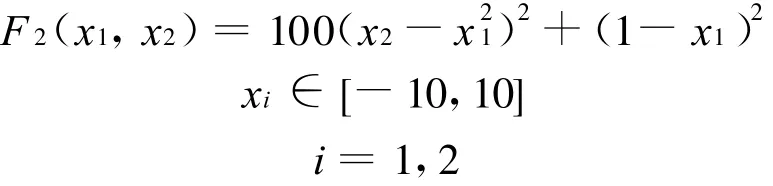
最优解（1，1）T，

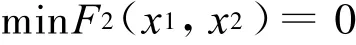
根据文中的方法，投点数N=2 000，迭代次数k=4，得到最优解（1，1）T，

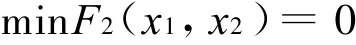
例2 Easom（ES）函数:

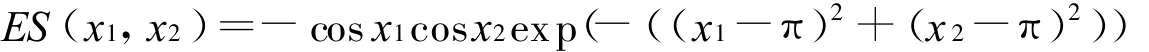
搜索范围:-100＜xi＜100，i=1，2;

全局最优解:

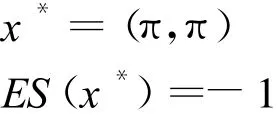
通过文中的算法，当N=4 000，k=3时，最优解为（3.1423，3.148 9）T，最优值为-0.999 989。

例3 Sphere Model函数:

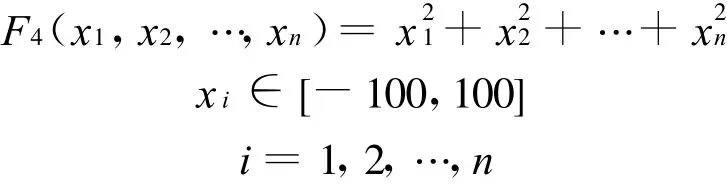
取n=3，最优解xi=0（i=1，2，3），

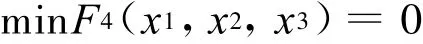
根据文中算法，当N=3 000，k=5时，得到最优解（0.002 0，0.001 9，0.002 1）T，

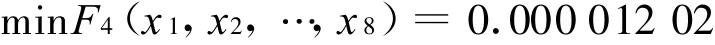
3 结 语

给出了求解全局优化问题的一个新方法——基于视觉认知的全局优化算法，确保在产生眺望点时，不存在漏点的现象，且用数学方法证明了由算法产生的序列依概率收敛于全局最小值，通过以上数值例子对算法加以实现，结果表明算法具有可行性和有效性。

[1] Glover F.Tabu search:partⅠ[J].ORSA Journal on Computing，1989，21（1）:190-206.

[2] Glover F.Tabu Search:partⅡ[J].ORSA Journal on Computing，1990，22（2）:4-32.

[3] Lundy M，Mess A.Convergence of an annealing algorithm[J].Math.Program-ming，1986，34（1）: 111-124.

[4] 刑文训，谢金星.现代优化计算方法[M].北京:清华大学出版社，2007.

[5] 汪定伟，王俊伟，王洪峰，等.智能优化方法[M].北京:高等教育出版社，2007.

[6] CAI Yan-guang，QIAN Ji-xin，SUN You-xian. Outlook algorithm for global optimiza-tion[J]. Journal of Guangdong University of Technology，2006，23（2）:1-10.

[7] De Boer.A tutorial on the cross-entropy method [J].Annals of Operations Research，2005，134（2）: 19-67.

[8] PENG Zheng，ZHANG Hai-dong，WU Dong-hua. A level value descent method forunconstrained global optimization problems[J].Applied Mathematics，2007，20（1）:213-219.

[9] 薛定宇，陈阳泉.高等应用数学问题的MAT LAB求解[M].北京:清华大学出版社，2008.