多项式函数极小化问题的全局优化算法

刘 巍， 谷 阔， 谭佳伟， 刘庆怀

（长春工业大学应用数学研究所，吉林长春 130012）

1 引言与问题提出

全局最优化问题是一类较难求解且非常重要的问题。在很多文献中可以发现有大量的文章是关于全局优化问题的。已有的全局优化算法大体可分为三类[1]:第一类是变换函数法，即利用辅助函数，从一个局部极小点出发，找到比这个局部极小点更优的另一个局部极小点（新局部极小点具有更小的目标函数值），如填充函数法[2]、打洞函数法[3]和水平值下降算法;第二类是适用于具有特殊结构的最优化问题（如D.C规划和不定二次规划的方法）;第三类是运用启发式搜索或随机搜索算法。例如模拟退火算法[4]、遗传算法、神经网络算法、禁忌搜索算法、蚁群算法、粒子群算法，然而，这些算法都有一定的局限性。

另外，对全局优化算法还进行如下研究:

1）混合方法。综合利用各种不同方法的优点，构造出性能比较良好的混合优化方法。

2）并行算法。考虑一种比较好的并行策略设计并行优化算法，文献[5-6]研究了一系列水平值估计算法，主要是采用一致分布的数值积分逼近水平集构造实现算法。

受水平值下降算法思想的启发，与传统优化算法-牛顿法相结合，针对多项式函数极小化问题提出一种新的求解一维无约束全局优化问题的算法。主要思路是先找到最优值的范围，然后找到对应的最优解。算法不仅具有大范围收敛性，而且收敛速度快。利用了多项式第二判别矩阵[7]降低了算法的整体复杂性，而且，由于其它所有函数都可以通过拟合等方法转化为多项式函数求解，所以，文中对多项式函数全局优化问题算法的研究可推广到其它函数。

考虑一维无约束全局最优化问题

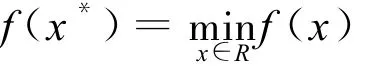
式中:f（x）——多项式函数。

2 基本概念与基本定理

定义1 设 f（x）=a0xn+a1xn-1+…+an，其导式记为:

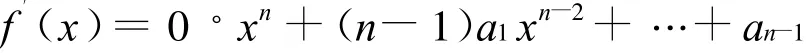
定义矩阵

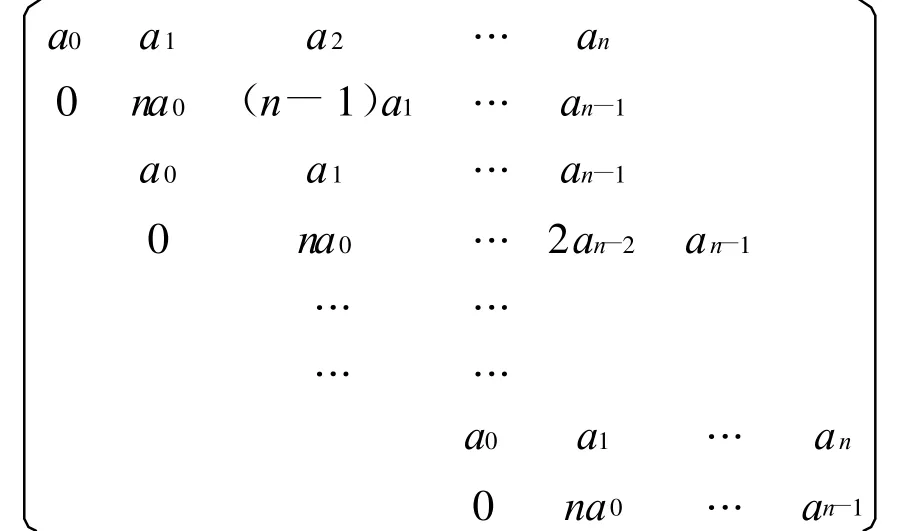
为多项式 f（x）的第二判别矩阵，记为Discr（f）。

定义2 设 f（x）是一个n次多项式。f（x）的判别式序列 D1（f），D2（f），…，Dn（f）就是f（x）的第二判别矩阵Discr（f）的偶阶顺序主子式序列;f（x）的重因子序列Δ0（f），Δ1（f），…，Δn-1（f）就是 f（x）与 f′（x）的子结式多项式序列。

2.1 符号修订规则

对于给定的有限个实数的序列l1，l2，…，ln（l1≠0），写出相应于这个序列的符号列 s1= sign（l1），s2=sign（l2），…，sn=sign（ln）。将[s1，s2，…，sn]叫做原序列的符号表。根据这个符号表可以定义一个符号修订表[ε1，ε2，…，εn]，其构造规则如下:

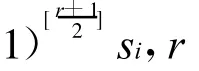
定理1 设σ0=1，σi=Dqi是n次多项式f（x）的判别多项式序列D1（f），D2（f），…，Dn（f）中第i个不等于零的项（i=1，…，k）。又设si=qi+1-qi-1（i=0，1，…，k-1;q0=0），判别式序列的符号修订表的变号数为ν。如果Dl（f）≠0，Dm（f）=0（m＞l），那么:

1）f（x）的互异共轭虚根对的数目为ν。

2）f（x）的互异实根个数为

3）α是 f（x）的 m重根，当且仅当 α是Δn-l（f）的m-1重根。

4）D1（f），D2（f），…，Dn（f）（除去一个正常数因子外）是无重根多项式 f/gcd（f，f′）的判别式序列。

2.2 牛顿法思想

设已知方程 f（x）=0有近似根 xk（假定f′（xk）≠0），将函数 f（x）在点 xk展开，有

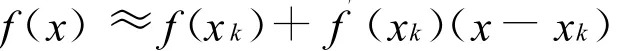
于是方程f（x）=0可近似地表示为

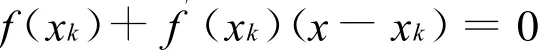
这是个线性方程，记其根为 xk+1，则xk+1的计算公式为

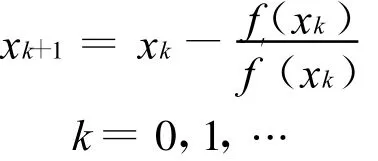
这就是牛顿法。

定义3 对于迭代过程xk+1=φ（xk），如果φ（p）（x）在所求根x*的邻近连续，并且

则该迭代过程在点x*邻近是p阶收敛的。

3 主要结果

3.1 算法步骤

步骤1:任意选取一初始曲线y0=f（x0），允许误差ε＞0，步长λ0=1，令k:=0，zk=f（x）-yk;

步骤2:判断zk=0是否有根，若有根，执行步骤3，否则转步骤4;

步骤3:令yk+1=yk-λk，k:=k+1，转步骤2;

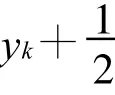
终止准则:若λk≤ε，且zk=f（x）-yk=0有解，停止，计算zk=f（x）-yk=0，输出k，yk，x*。

注:取x0∈（-∞，+∞），定义域f（x0）=y0。

3.2 算法收敛性分析

证明 如图1中，两条下降曲线之间的距离是步长λ0，设算法进行K次迭代的步长均为λ0，那么，若算法再经过n步结束，为方便这里n将记为k，则有

所以，k→∞，λk≤ε，即

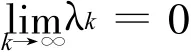
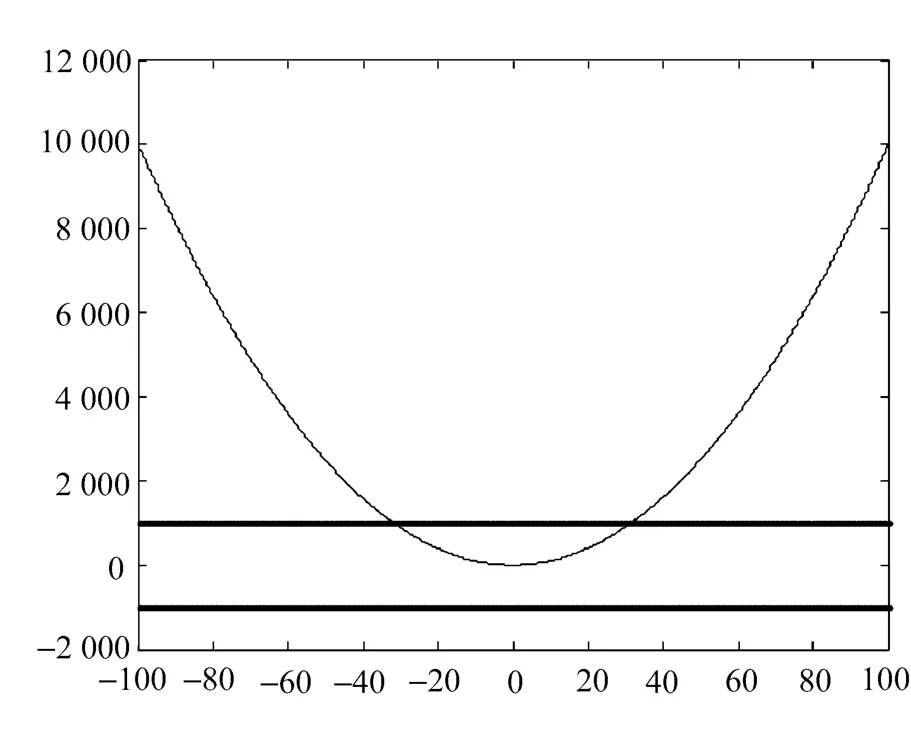
图1 水平值下降搜索示意图

定理3 yk是由算法所得到的迭代点列，则有

设算法经K次迭代后，有zk=f（x）-yk=0无根，即λk=λ0，那么设算法此后又经过n次迭代满足终止条件，有

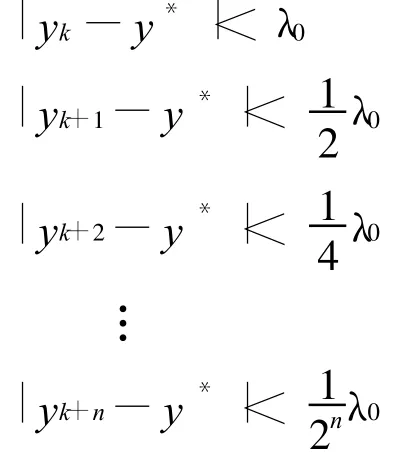
令K+n=k，所以

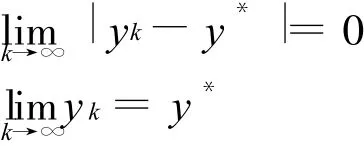
定理4 文中最后一步的求解过程采用牛顿法，令{xk}是由算法得到的序列，则该算法收敛。

证明:对

其迭代函数为

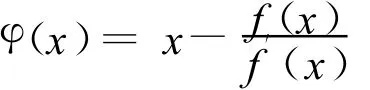
由于

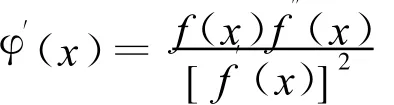
假定 x*是 f（x）的一个单根，则由上式知φ′（x*）=0，于是依据定义3可以断定，牛顿法在根x*的邻近是平方收敛的。

3.3 数值算例实现

例1:求x4-3x3+4x的极小值。

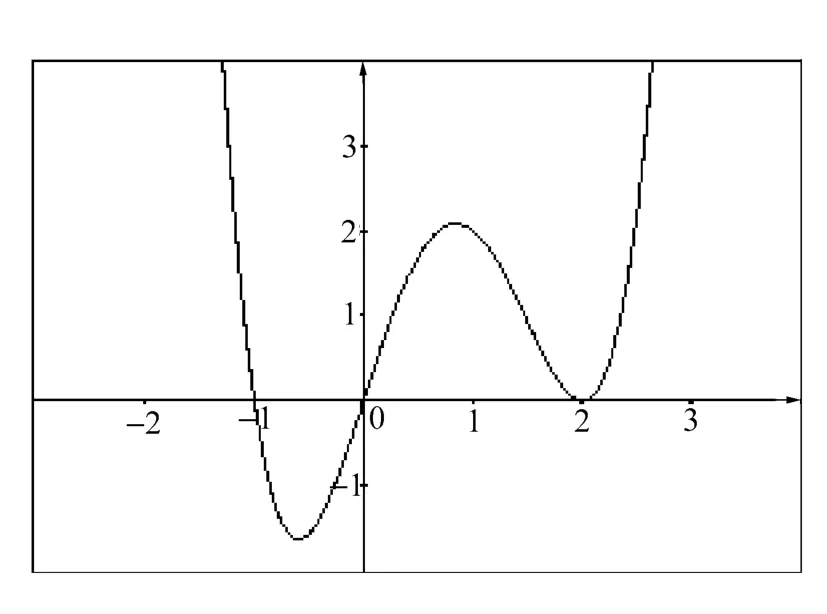
图2 例1图

取精度为 ε=10-4，最后的迭代步长为1.220 7e-004，最小值 x（n）=-2.999 8，迭代16步可找到最优值。最优解为-0.593 1。

4 结 语

文中算法具有大范围收敛性，利用了多项式判别矩阵，使算法的整体复杂性降低。同时与其它算法的差别之处是先寻找最优值的范围，可以判断出最优值的范围（yk-λk，yk），最后求得最优解。由于其它所有函数都可以通过拟合等方法转化为多项式函数求解，所以文中对多项式函数全局优化问题算法的研究可推广到其它函数。另外，文中方法经过技术转换还可推广到一般n维空间的全局优化问题中，这是后续工作。

[1] 陈冬芳，薛继伟，张漫.全局最优化算法及其应用[J].大庆石油学院学报，2005（1）:89-93.

[2] Ge R P.The theory of filled function methods for finding global minimizes of nonlinearly constrained minimization porblems[J].Journal of Computation Mathematics，1987，5（1）:129.

[3] Cetin B C，Barhen J，Burdick J W，et al.Terminal repeller un2constrained subenergy tanneling（TRUST）for fast global opti2mization[J].Journal of Optimization Theory and Applications，1993，77（1）:97-126.

[4] 刑文训，谢金星.现代优化计算方法[M].北京:清华大学出版社，1999:90-138.

[5] 彭拯，张海东，邬冬华.一种无约束全局优化的水平值下降算法[J].应用数学，2007，20（1）:213-219.

[6] 彭拯，邬冬华，田蔚文.约束全局最优化的水平值估计算法[J].计算数学，2007，29（3）:293-304.

[7] 杨路，张景中.侯晓荣.非线性代数方程组与定理机器证明[M].上海:上海科技教育出版社，1996:160-163，144-145.