离散系统有限时域H∞滤波器设计

（海军航空工程学院系统科学与数学研究所，山东 烟台 264001）

0 引言

滤波是一种对信号的处理技术，它是指对所接收到的受到干扰因素影响的信号进行处理，得到相关信号的估计值。滤波问题出现在大量的工程问题中，具有重要的研究价值。传统的Kalman 滤波器利用状态估计的方法，使估计的均方误差最小，Kalman 滤波器被成功应用到控制与信号处理的各个领域。但Kalman 滤波方法要求所研究的动力系统是适定的而且外部噪声须是具有静态特性的白噪声。然而在实际应用中，这些条件并不能经常满足，应用标准的Kalman 滤波器算法不能得到令人满意的结果。为了拓广滤波技术的应用范围，1989年，A.Elsaye 引入H∞滤波概念[1]。H∞滤波就是设计一个滤波器使得从干扰输入到估计误差输出的H∞范数最小。H∞滤波的主要优点在于无须假设干扰信号的统计特性，这样更符合实际的应用。H∞滤波的这一优点使得它在雷达设计、故障检测、信号处理等领域得到了广泛的应用[2-4]。

无穷时域的H∞滤波问题一直备受关注并取得了一系列重要结果[5-7]。近年来，有限时域的H∞滤波问题也受到越来越多的学者的关注，由于很多控制任务都是在指定的有限时间内完成的，所以研究有限时域的H∞滤波问题不仅具有理论意义而且更具有实际意义。文献[8]研究了连续和离散线性系统的有限时域H∞滤波问题，借助于伴随系统，将H∞滤波器的求解问题转化成对一个Riccati 微分（差分）方程的求解。文献[9]用类似的方法研究了时变离散随机系统的有限时域H∞滤波问题，并运用得到的结果解决了相应的输出反馈控制问题。文献[8-9]都通过求解Riccati 方程的方法来得到相应的H∞滤波器，Riccati 方程方法具有参数不易调整，求解困难等缺点。

本文研究一类离散系统的有限时域H∞滤波器的设计问题。提出了有限时域H∞滤波器存在的充分条件，同时利用线性矩阵不等式（LMI）给出了滤波器设计的一个构造性方法。该法可通过Matlab工具箱实现，易于求解操作。数值仿真实例表明，由这一方法设计的H∞滤波器具有良好性能。

本文使用符号说明：

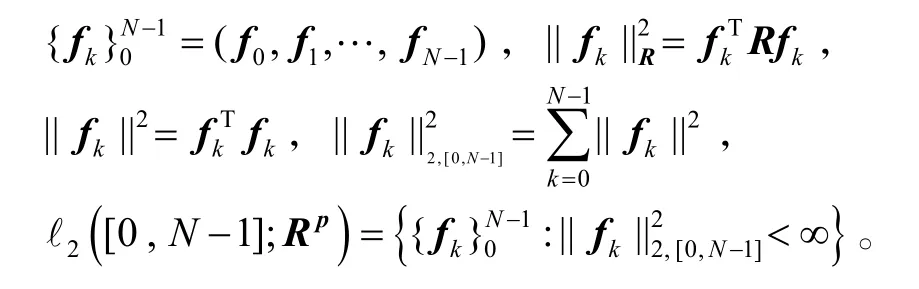
1 问题描述和准备

考虑如下的离散系统：

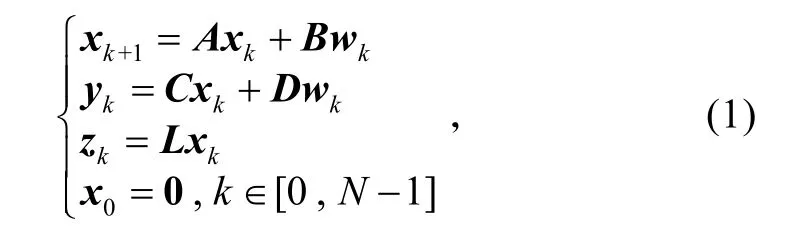
式中：xk∈Rn是系统的状态变量；yk∈Rm是测量输出；wk∈ ℓ2([0,N−1];Rp)是能量有限的噪声信号（包括过程和测量噪声）；zk∈Rr是待估计的信号；A、B、C、D为具有相应维数的已知矩阵。

滤波的目的就是根据系统输出 yk找出状态向量的组合 zk=Lkxk的一个估计zk，使得估计误差的信号能量与干扰能量的比小于预先指定的数γ 。在有限时间下，意味对于任何 wk∈ ℓ2([ 0, N−1]; Rp)，设计滤波器

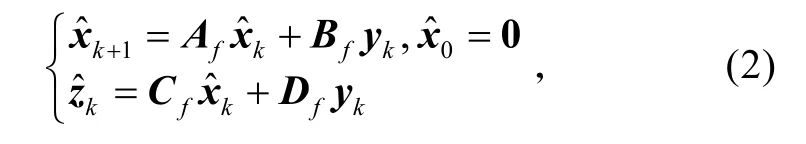
满足

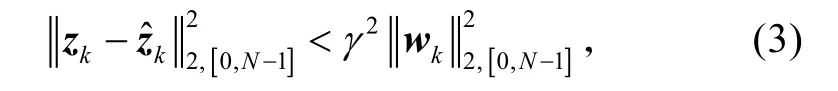
式中：Af、Bf、Cf、Df是H∞滤波器(2)的待求系数矩阵。

由系统(1)、(2)可得增广系统方程为

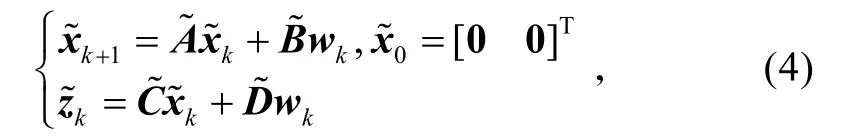
相应地，式(3)转化为

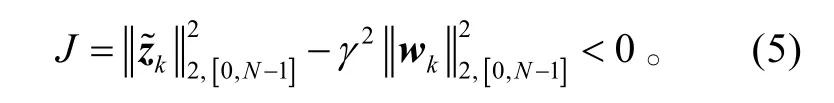
本文的目的是对离散系统(1)研究满足性能指标(5)的H∞滤波器的设计方法，给出了滤波器存在的充分条件，同时利用LMI方法给出了滤波器(2)的构造性的设计方法。

为了得到本文的主要结论，先给出一个重要引理，借助这个引理，可以推导出本文的主要结论。

引理1[10]给定适当维数的矩阵X、Y 和任意常数α＞0，其中X可逆，那么

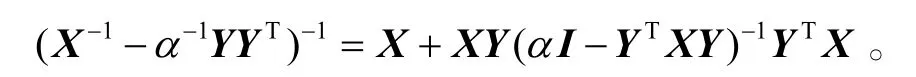
2 主要结论

定理1考虑系统(4)。对于给定的常数γ ＞ 0，对所有的wk∈ ℓ2([0,N−1];Rp)，式(5)所定义的性能指标J＜0成立的充分条件是存在对称正定矩阵Q 满足

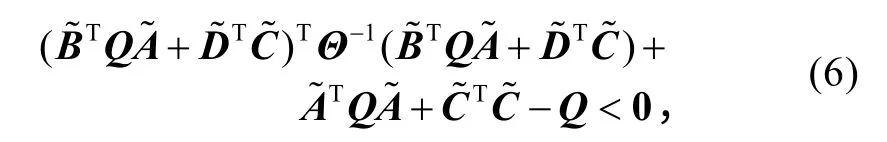
证明：定义李雅普诺夫函数并作差分将代入 Jk中，得

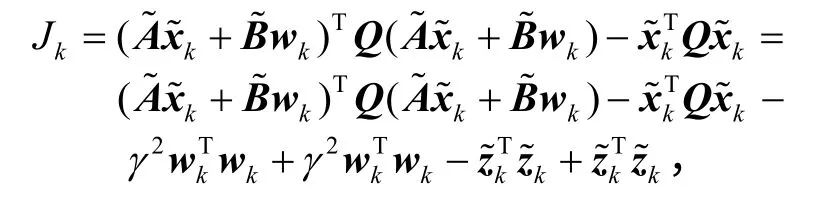
也就是

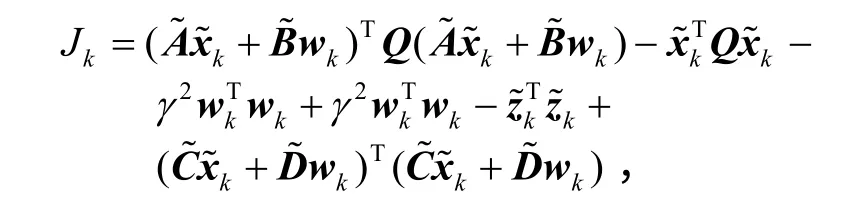
整理得到

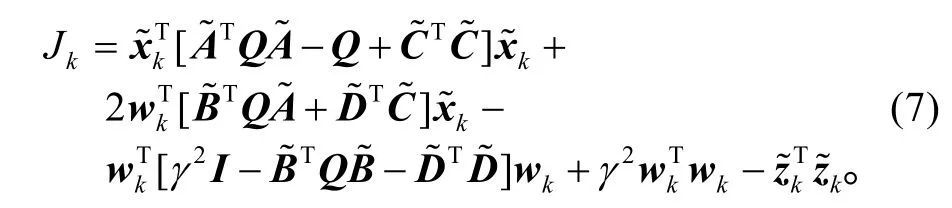
令

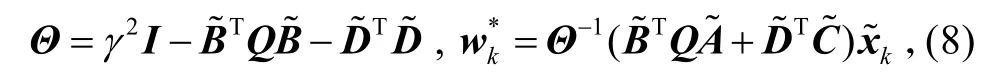
则式(7)经过化简整理可以得到

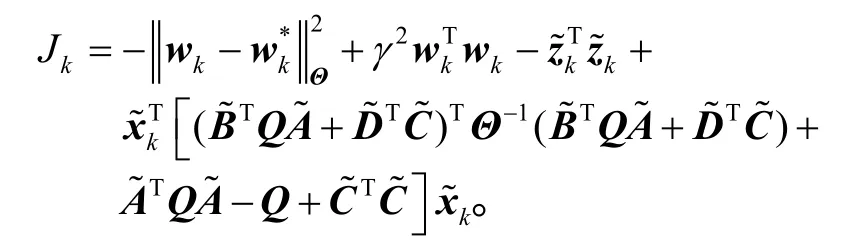
再令

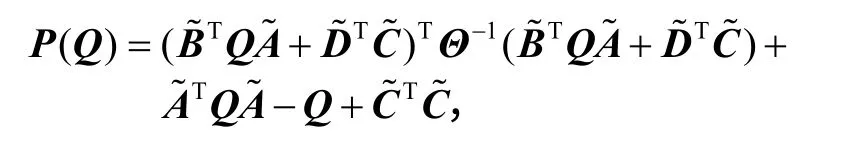
则

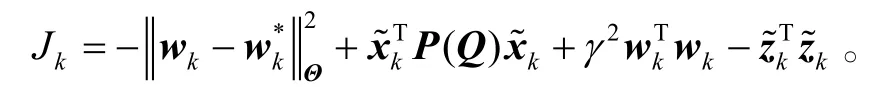
将上式从k=0到 k=N− 1求和，可得

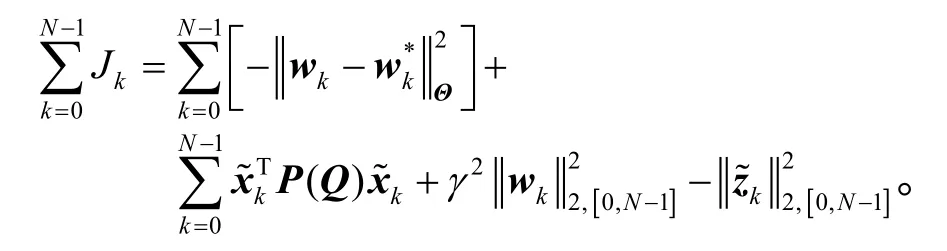
又由于

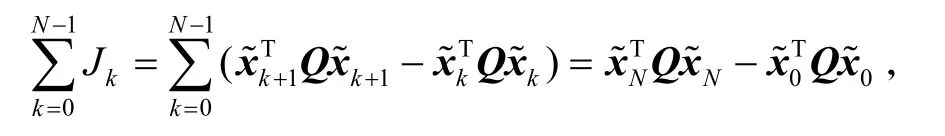
则

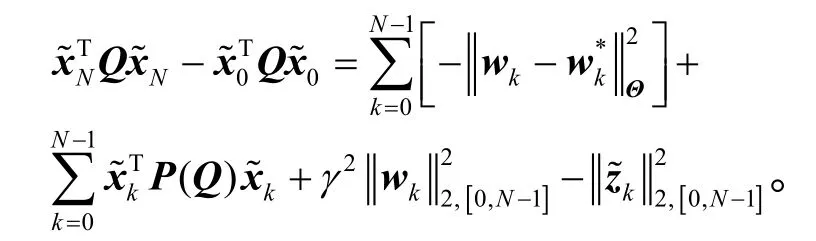
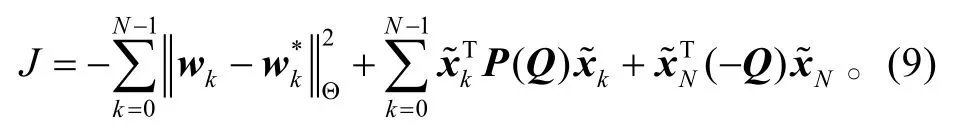
由式(6)，P (Q)＜0，可得到J＜0。即，若存在对称正定矩阵Q 满足式(6)，则性能指标J＜0 成立。证毕。

要通过式(6)求解滤波器是很困难的事情。为了克服这一困难，我们提出下面的定理2。定理2 借助于线性矩阵不等式给出了一个与定理1 等价的滤波器存在的充分条件，同时给出了滤波器的设计方法。

定理2考虑系统(1)。对于给定的常数γ ＞0，如果存在对称正定阵∆、Y 和矩阵E、F、G、H 使得线性矩阵不等式(10)和线性矩阵不等式(11)成立，则H∞滤波器(2)存在。

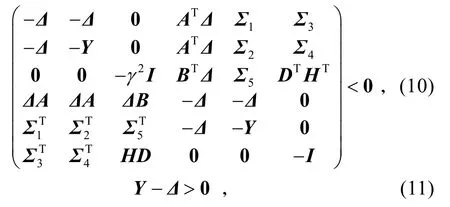
式中：

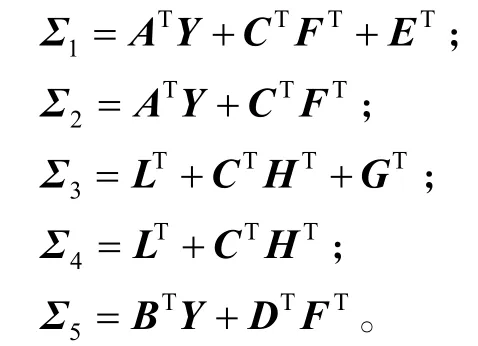
进一步，若∆、Y、E、F、G、H是矩阵不等式(10)和(11)的可行解，则通过矩阵 I −∆−1Y的奇异值分解可以得到满秩矩阵W、V，并可利用下式求得H∞滤波器(2)的系数矩阵：

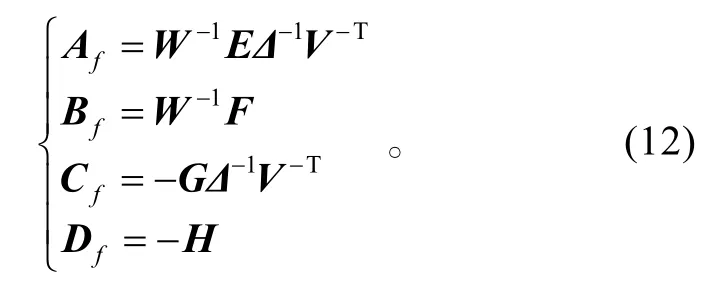
证明：由定理 1可知，如果对所有的存在对称正定阵Q 满足式(6)，则性能指标J＜0 成立。

记

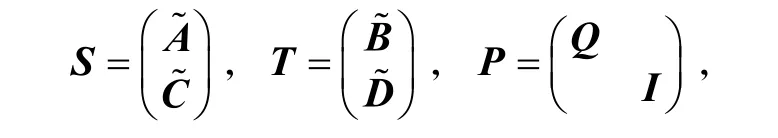
则式(6)变形为

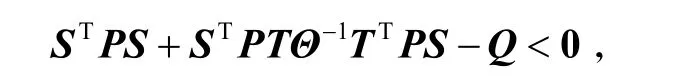
式中：Θ=γ2I − TTPT ＞0，

即

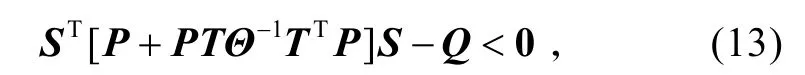
式中：Θ=γ2I − TTPT ＞0。

进一步，利用引理1，可以将式(13)化简为

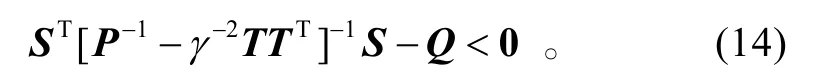
利用矩阵Schur 补性质，式(14)成立当且仅当

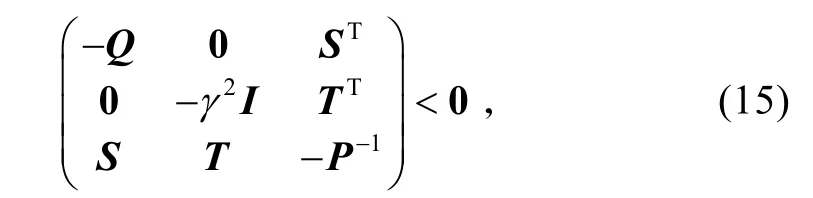
即

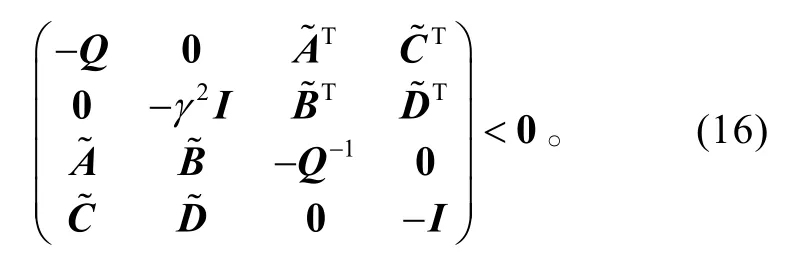
令 Q=R−1，则上式变为

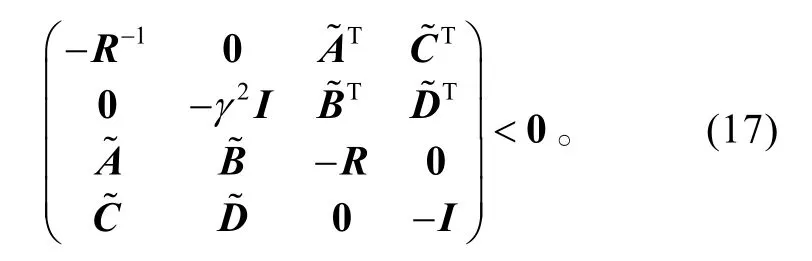
考虑到矩阵不等式(17)是矩阵变量R、Af、Bf、Cf、Df的一个非线性矩阵不等式，要直接从该矩阵不等式中求出可行的矩阵变量R、Af、Bf、Cf、Df是非常困难的。

在这种情况下，采用变量替换的方法，设法将矩阵不等式(17)转化成一个线性矩阵不等式，从而可以应用LMI 工具箱中的求解线性矩阵不等式的有效方法来设计H∞滤波器。

对矩阵R 和逆矩阵 R−1进行以下分块

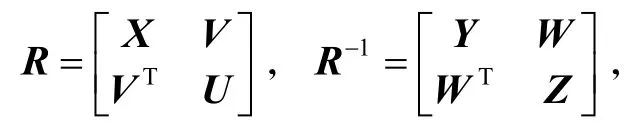
式中：X ∈ Rn×n、Y ∈Rn×n是对称正定矩阵。

从等式RR−1=I可得也就是VWT=I −XY，VTY + UWT=0，据此，进一步可得

通过计算可以验证 R＞0等价于

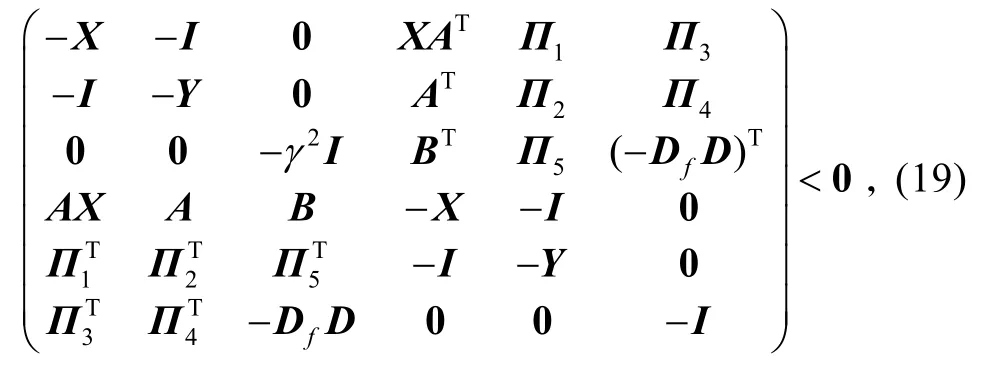
式中：

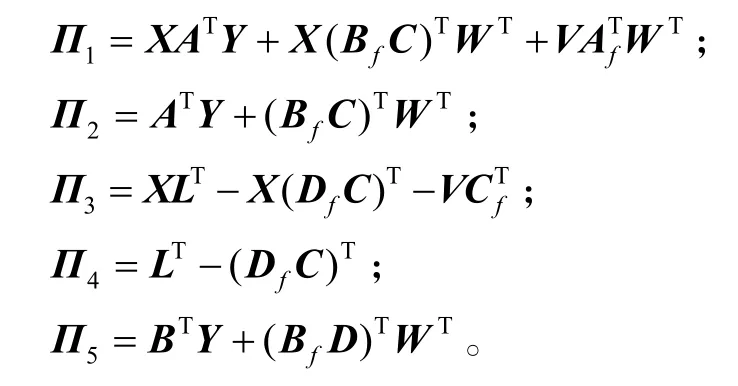
再次用 diag{X−1,I,I,X−1,I,I}左乘和右乘式(19)，则可得矩阵不等式

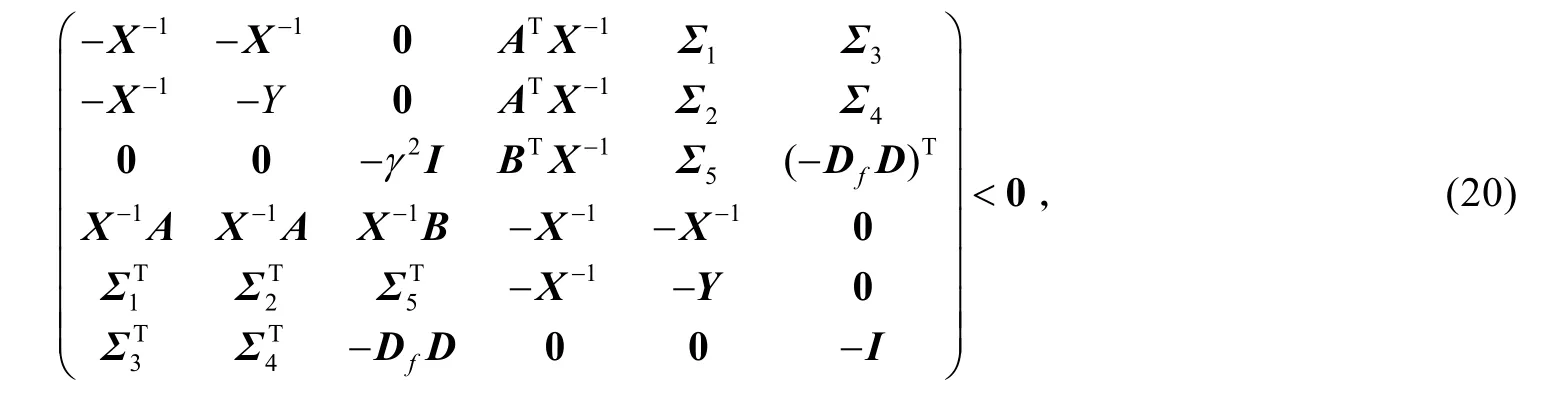
式中：

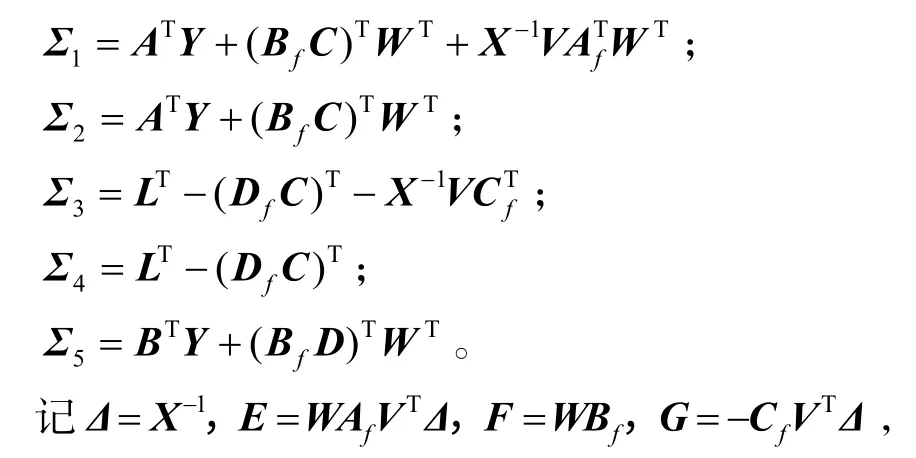
H=−Df，则矩阵不等式(20)变为

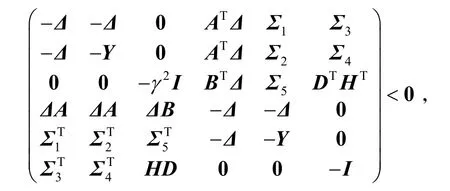
式中：

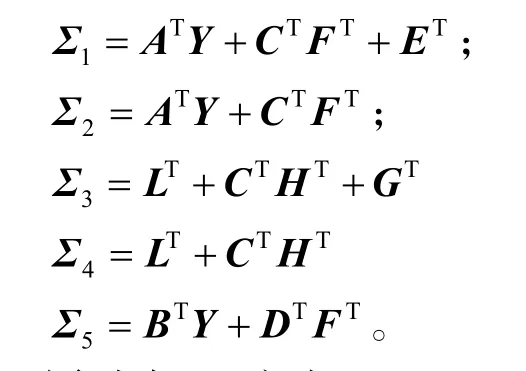
同时式(18)变为Y − Δ ＞0。

进一步，若Δ、Y、E、F、G、H是矩阵不等式(10)、(11)的可行解，则通过矩阵 I −Δ−1Y的奇异值分解可以得到满秩矩阵W、V，进而可以利用下式给出H∞滤波器(2)的系数矩阵：

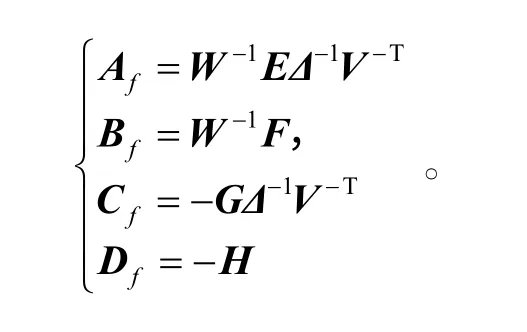
证毕。

3 仿真实例

考虑如下的离散系统

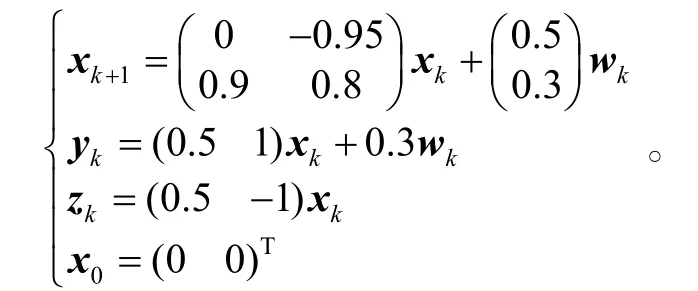
取γ=1，N=100。

利用Matlab 中的LMI 工具箱，求得H∞滤波器的系数矩阵如下

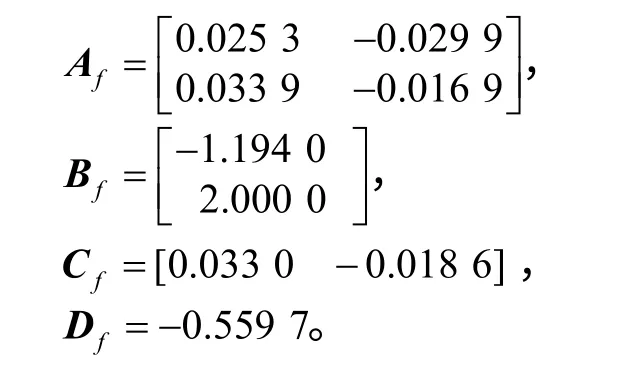
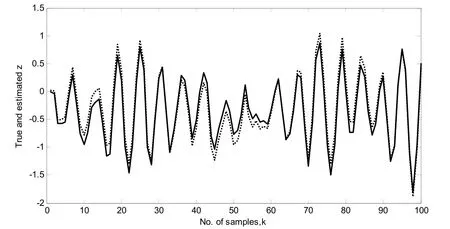
图1 待估计信号 z (k)和估计信号的曲线

在图1中，实线表示待估计信号 z (k)曲线，虚线表示估计信号曲线。通过仿真例子结合得到的仿真图形，我们可以看出本文提出的H∞滤波器的设计方法不仅满足性能指标，而且结果有效，说明该滤波器性能良好。

4 结语

本文针对受到外部干扰的离散系统，研究了有限时域H∞滤波问题。提出了有限时域H∞滤波器存在的充分条件，并且借助线性矩阵不等式，给出了H∞滤波器的设计方法。避免了用Riccati 方程求解滤波器参数时的困难。最后通过仿真实例说明了本文方法的有效性和可行性。

[1]ELASYED A,GRIMBLE M J.A new approach to the H∞design of optimal digital linear filters[J].IMA Journal of Mathematical Control and Information,1989,6(2):233-251.

[2]陈莉,钟麦英.不确定奇异时滞系统的鲁棒H∞故障诊断滤波器设计[J].自动化学报,2008,34(8):943-949.

[3]丁兴俊,周德云,董朝阳.基于H∞滤波的主/被动雷达模糊自适应融合算法[J].导弹与航天运载技术,2007(1):46-49.

[4]于德新,潘爽.基于H∞滤波技术的GPS 动态定位研究[J].计算机仿真,2008,25(2):306-309.

[5]PALHARES R M,PERES P L.Robust H∞filtering design with pole placement constraint via LMI[J].Journal of Optimization Theory and Applications,1999,102(2):239-261.

[6]林岳松,薛安克,钱积新.基于LMI方法的鲁棒H∞滤波器设计[J].电路与系统学报,2004,9(5):81-85.

[7]ZHANG WEI HAI,CHEN BOR SEN,TSENG CHUNG SHI.Robust H∞filtering for nonlinear stochastic systems[J].IEEE Trans.Signal Processing,2005,53(2):289-298.

[8]GREEN M LIMEBEER,DAVID J N.Linear robust control[M].Englewood Cliffs:Prentice Hall,1994:265-268.

[9]GERSHON E,SHAKED U,YAESH I.H∞control and filtering of discrete-time stochastic systems with multiplicative noise[J].Automatica,2001,7(3):409-417.

[10]HUNG Y S,YANG FUWEN.Robust H∞filtering with error variance constraints for discrete time-varying systems with uncertainty[J].Automatica,2003,39(7):1185-1194.