极小值搜索与平方和转化求解多元非线性方程组
李建文, 张成现, 李 颀, 马学宗
(1.陕西科技大学电气与信息工程学院, 陕西 西安 710021;2.西安工程大学计算机科学学院, 陕西 西安 710048)
0 引言
多元非线性函数的极值数值解问题是一个非常普遍的数学问题,在理论上往往把多元非线性极值问题归结为多元非线性方程组的求根问题[1-3],但实际上多元非线性方程组的求根问题比多元非线性函数极值问题更难解决.在计算数学中为了解决多元极值问题引出了许多新的方法,如最速下降法、遗传算法、边缘检测算法等[4-6].
现在,由于微型计算机的普及和微型计算机软件的快速发展,人们普遍使用Matlab来解决数值计算问题[7,8].但Matlab的求根能力很有限,它不但速度慢,而且还对许多简单的方程组无法求解.
作者在解决石英晶振体热敏网络温度补偿问题时总结出了一种新的用于计算机查找极值的方法“多元非线性函数极值的微分搜索算法”,以后又将这种方法用在其它许多领域,如语音基频分析、彩色电视机荫罩曲面求解等[9,10].通过实际使用证明,这种方法比教科书里所提到的所有查找极值的方法都方便,而且还可以将多元非线性函数极值、多元非线性方程组、任意隐式微分方程等一系列的数值计算问题一并解决.在此,作者将这种新方法与传统的牛顿迭代法进行比较.
1 传统迭代法及其缺点
设多元非线性函数为f(x1,x2,…,xn),根据微分原理,在多元非线性函数的极值点上各个分量的微分值必然为0,所以通过解如下的非线性方程组

(1)
必然获得到极值点的坐标.传统上都使用牛顿迭代法求解这个非线性方程组[2].
求解过程可以划分为:求偏导、列方程组、非线性方程组线性化、得出含(n+1)×n矩阵的n阶线性方程组、选迭代初值、迭代[1,2],这种迭代的运算量级为n2,因此其过程十分复杂,尤其是当一个非线性多元函数的表达式很复杂时它的偏导函数的表达式更加复杂,对于一个非常复杂的非线性导函数方程组线性化需要忽略许多相关因素,这必然造成结果的不准确性,之后的迭代初值如果选取不合适会造成迭代过程发散,等等,并且其中每一个过程的实现都是极其困难的.
实际上这种求极值的方法把问题反而复杂化了,在实际中很难被使用,很多情况是不能使用.后面还有实例说明.
另一种常用的算法称为最速下降法.最速下降法是根据多元函数的梯度的反方向进行搜索,仍然需要求偏导,还需要选择一个步长.这种方法的收敛速度是线性的,在开始几步以后其收敛速度变得很慢.
作者在本文中给出了一种用于求解非线性多元连续函数极值问题的通用搜索算法,其使用过程相当简单,仅仅需要选取初值、迭代即可,求偏导、列方程组、非线性方程组线性化等过程全部可取消,而且这种算法已经做成了计算机软件,经过大量高难度解方程和求极值验证其成功率达100%.
2 自适应极值搜索法
这里所说的“自适应极值搜索法”是作者在解决极值问题时构思的,不但完满地解决了所有的极值计算问题,而且具备许多优势.
这里以搜索极小值为例进行讲解,图1 是一种简化过的模型,实际问题是在n维空间解决的,但为了说明问题方便,以2维空间为例.设(x0,y0)为定义域内任意一点,并选取适当的域半径Δx、Δy以保证周围的4个点也在定义域内.总的原则也是逐次逼近真正的极小值点,逼近是通过两个方面进行的,即移动中心点和缩小域半径Δx、Δy.主要的方法是分别考察每个分量方向的3点上函数f(x,y)的最小值落在何处,由于是有限个点,所以必然在其中某个点上达到最小值.
在X轴方向考虑(x0-Δx,y0)、(x0,y0)、(x0+Δx,y0),如果f(x,y)在(x0,y0)点上达到最小,说明f(x,y)的极小值点在(x0,y0)附近,这时不应该移动中心点,而应该缩小域半径,所以用k1Δx代替Δx.如果f(x,y)的极小值点不在(x0,y0)上达到,应该更换中心点,再看在 (x0-Δx,y0)或(x0+Δx,y0)哪个点上的f(x,y)的函数值小就用哪个点代替(x0,y0),这时要查找的极值点可能距离(x0,y0)很远,为了提高逼近速度,所以用k2Δx代替Δx.
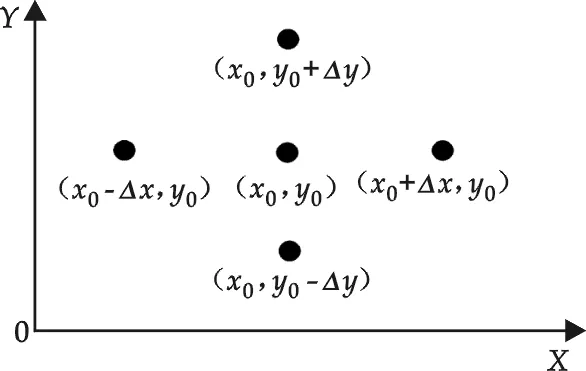
图1 二维坐标系缩放半径与移动中心点示意图
同理,在Y轴方向考虑(x0,y0-Δy)、(x0-y0)、(x0,y0+Δy) 3个点,以决定是否在Y轴方向移动(x0,y0),如果不移动就将Δy缩小到原来的k1≤0.5;如果移动就将Δy放大到原来的k2>1.经过作者的大量实验证明,k1≈0.19~0.27,k2≈1.31.
如此循环进行,便会依次得到若干个f(x,y)的值f0,f1,f2,…,fi,…而且它们均满足f0>f1>f2>…>fi>…. 如果这些函数值是有界的,则根据有界单调序列必然收敛的原则,可以得到极小值点.如果要求出定义域内的所有极值,可以将定义域划分成足够小的网格,在每个网格内选取初值进行搜索,便可获得全部的极值点.
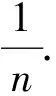
极值搜索算法比求解多元非线性方程组简单得多,所以它应该是更基本的算法.
综合上述,我们得出:
定理1:多元函数的极小值可以通过搜索得到.
3 可归结为求极值的若干数学问题
3.1 多元非线性拟合问题
多元非线性拟合就是一个非负极小值问题.
设f(x)是定义域[a,b]上的一元非线性函数,x1,x2,…,xn是[a,b]上的点,想求得带有m个参数的φ(x;λ1,λ2,…,λm).需要确定合适的λ1,λ2,…,λm,使得
(2)
达到最小.这显然是一个m元非线性函数的极小值问题,很容易通过极小值搜索实现.但几乎所有的教科书都错误地认为这样的非线性残差和问题无法求得,即使能求得也只能是一些特殊情况,如要通过显性化或牛顿迭代法求解[1-3].
3.2 多元非线性方程组求根问题
利用g(x)=[f(x)]2可以将任意一元方程求根问题转化为极小值的求解,一元极小值更容易实现;
设
f1(x1,x2,…,xn)=0
f2(x1,x2,…,xn)=0
……
fn(x1,x2,…,xn)=0
(3)
是n元的非线性方程组.令
(4)
则,当且仅当全部的fi(x1,x2,…,xn)=0时g(x1,x2,…,xn)=0,这样便将任意多元非线性方程组的求根问题转化为多元非线性极小值的求解.极小值为0或接近0时的解便是方程(3)的解,所以我们得到:
定理2:通过平方和可以将多元非线性方程组问题转化为多元函数的极小值问题.
使用这种方法求解时,即使没有解也能找到最接近的解.
4 使用效果比较与优越性
这种极值搜索法与牛顿迭代法相比有着绝对的优势,如对于方程:
(5)
利用这种方法求解时,Intel Pentium双核2.8 GHz CPU环境下单次计算逼近770次仅需0.005 s,可求得

(6)
与零点的接近程度为3.527-16,这是双精度数据类型最高程度,这样的计算连续200次时仅需1s.如果使用牛顿迭代法求解,可使用Matlab7.0或Matlab7.1在提示方式下键入:
[x,y]=solve(′(exp(sin(x)))∧4+(exp(cos(y)))∧2=1′,′exp(x)+exp(y)/2=1′)
(7)
会造成Matlab死锁,无法求解.其实这也不难理解,因为Matlab中所使用的牛顿迭代法往往收敛速度特别慢,还可能是不收敛的.
极值搜索法有如下优点:
(1)设计程序时只要函数的表达式,无需求偏导函数,简化了推导过程;
(2)仅要求连续即可,如果可导则更好,条件十分宽松;
(3)求多元非线性函数极值时无需解多元非线性方程组,更无需线性化;
(4)不管选取任何初值,迭代过程不发散,即使极值点在边界上也能找到;
(5)采取不同的初值重复使用这种方法可搜到所有的根或者极值;
(6)结束条件也很容易实现,只要限定域半径,所以在计算机上很容易实现;
(7)由于计算过程自动调节步长,所以收敛速度是非线性的;
(8)由于是验证性搜索,精度特别高,可以达到最高程度;
(9)由于论述过程未曾涉及具体函数,所以这种方法与函数表达式无关,适用于任何函数.
5 任意隐式微分方程数值求解
任意隐式微分方程数值求解是数值方法教科书回避的难题,用本文的方法可以彻底解决这个问题,其基本原理是先将微分方程转化为方程求解.
设初值问题
(8)
是定义于区间[a,b]上的隐式微分方程,我们仍然可以沿用欧拉折线的思想.设x0 这时微分方程(8)便成为: (9) 这显然是一个关于yn的非线性方程.而通过前面的论述可知,非线性方程问题可以很容易通过极小值搜索来解决,而y(x0)=y0是已知的,因此很容易先求得y1,然后依次求得y2,…,yn-1,yn….注意,由于这里每次都是通过搜索极值得到的函数值yn=y(xn),精度远远高于欧拉单步法及其改进型所得到的结果,所以还可以肯定地说,我们不但能够求解隐式的微分方程,还可以得到比欧拉方法更为准确的解. 方程(8)还可以扩充为n阶.通过类似的方法,我们也不难证明所有的偏微分方程初值问题很容易归结为多元非线性方程组,进而通过极小值搜索得到解决. 由于多元函数的极小值可以通过搜索得到(定理1),通过平方和可以将多元非线性方程组问题转化为多元函数的极小值问题(定理2),所以我们可以得出重要的定理3. 定理3只要我们把某个数学问题归结为连续函数求极值或者解方程,那么就应该认为这个问题已经获得了解决. 在现有的数值方法教科书中,通过求偏导后将极值问题转化为求解非线性方程组,而我们现在求极值的方法反倒变得简单了,而且在这里反倒将非线性拟合与多元非线性方程的求根问题全部归结为极小值问题. 目前,几乎所有的数值方法教书里都是以牛顿迭代法作为求解非线性方程组的基本方法,进而涉及非线性多元函数的极值问题.在许多教科书中都认为非线性多元函数的极值问题无法解决[1-3,7],所以在非线性回归的问题中又要使用“非线性函数线性化”,如果实在无法线性化便认为非线性回归问题无法解决.事实上在非线性回归问题无需线性化[9,10],我们只要使用好搜索法. 由于计算机普遍使用,极值搜索方法确实是非常实用而且容易实现的,传统的数值方法理论应该全面修正.确切地说,在数值方法教科书中应该将极值搜索作为基本算法而不是牛顿迭代法. [1] 徐翠薇.计算方法引论[M].北京:高等教育出版社,1999:59-67,202-205. [2]蔺小林,蒋耀林.现代数值分析[M].北京:国防工业出版社,2004:116,245-254. [3]何晓群.实用回归分析[M].北京:高等教育出版社,2008:182-188. [4]赵明旺.基于遗传算法和最速下降法的函数优化混合数值算法[J].系统工程理论与实践,1997,7:59-64. [5]苑玮琦,王建军,张宏勋.一种基于梯度极值的边缘检测算法[J].信息与控制,1997,26(2):117-120. [6]周立华,罗隆福.遗传算法及其在求极值方面的应用[J].湖南工业职业技术学院学报[J]. 2003,3(3):6-8. [7]李 丽,王振领.Matlab工程计算及应用[M].北京:人民邮电出版社,2003:175-183,203. [8]张 磊,毕 靖,郭莲英.Matlab使用教程[M].北京:人民邮电出版社,2008:165-166. [9]李建文.热敏电阻网络非线性补偿的通用拟合算法[J].传感器技术,2001,20(11):44-46. [10]张成现,李建文.多元非线性函数极值的通用数值解法[J].西安工程科技学院学报,2005,19(4):507-509.6 结束语

