新型自吸式搅拌装置流量的简化计算方法研究
董林福, 罗 鹏, 黄颜锋
(沈阳化工大学机械工程学院,辽宁沈阳110142)
对于间歇操作的利用夹套加热的蒸发器,随着蒸发过程的进行,液位会出现较大幅度的降低.如果出现这种情况,设备的传热面就不能得以充分利用[1].文献[2]提出了一种具有自吸功能的搅拌桨[1],这种搅拌桨(如图1所示)除具有搅拌混合作用外,还能将较低液位的物料喷洒在夹套的加热内壁上,大大提高了设备的热效率.在设计此类搅拌装置时,预测装置的最大自吸流量非常重要.本文从流体静力学的基本状态方程出发,利用能量守恒法则推导出搅拌装置流量的简化计算方法.为验证这种计算方法的有效性,利用不同夹角的搅拌管自吸式搅拌装置中的实验数据,证实这种搅拌装置流量简化计算方法的可行性.
1 自吸式搅拌装置的工作原理
自吸式搅拌装置的结构如图1所示.它主要由搅拌轴1、若干个搅拌管3、容器2和夹套4所组成.搅拌管成一定角度对称布置,与搅拌轴组成搅拌桨.根据工艺要求,夹套要进行加热(或冷却),以使容器对物料产生换热作用.物料从下端管口进入到管内,并随管子转动,在离心力的作用下,沿倾斜搅拌管上升,最后从上管口喷出.从搅拌管倾斜喷出的液体喷洒在位于液位之上夹套容器的内壁上,并沿容器的内壁流下.由于从夹套内壁流下的液体液层很薄,从而使换热表面得以充分利用,加快了蒸发、蒸馏等过程的速度.

图1 夹套容器及自吸式搅拌装置Fig.1 Schematic diagram of jacketed tank and self-suction stirrer
2 简化计算
将液体在导管内的状况简化成具有不同直径的圆柱式容器(如图2所示),在容器以角速度ω作等角速度回转的过程中,液体质点微团满足静力平衡条件.假想筒柱有足够高,则液体在各筒体内部保持平衡,液体质点与质点之间不再有相对运动,液体连同筒体作整体回转运动.由于筒体内液体在容器静止时液面高度可通过测量求得,依据等角速度旋转液体平衡的条件,可求出液体能达到该筒体内的最高点.如果设筒体内液体没有达到最高处,则其必具有一定的动能,根据能量守恒定理的动能与势能的相互转化关系,可求出动能,并得到相应位置液体质点的平均速度(在此只考虑存在2种能量形式).
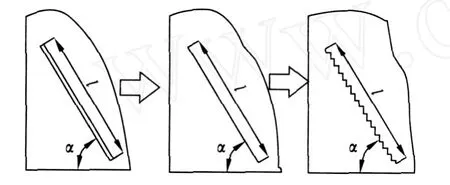
图2 容器结构简化过程Fig.2 Predigest process of tank's structure
容器作等角速回转运动,如图3所示.盛有液体的容器绕铅直轴作回转运动,启动瞬间,液体被甩向四周,但当回转角速度ω稳定不变时,液体形成如图3所示的自由表面,质点与质点之间不再有相对运动,液体连同容器作整体回转,如果将运动坐标系固结在回转容器上,且如图3(a)所示,坐标原点取在液面最低点,则液体对运动坐标系形成相对平衡(图3(a)中用M表示液面).
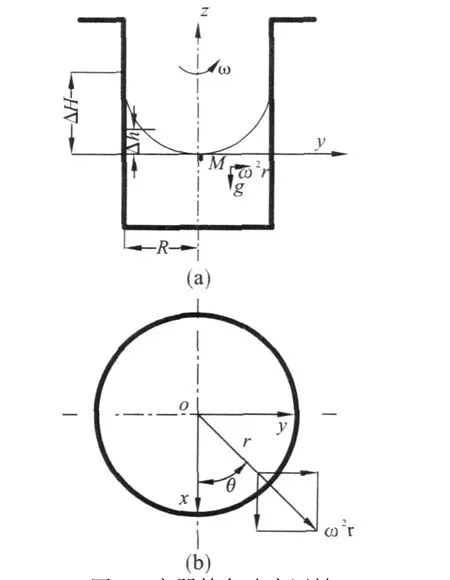
图3 容器等角速度回转Fig.3 Turnning of bank on the contour velocity
此时作用在液体上的质量力有2种:一种是重力ΔW=Δmg;一种是虚构的离心惯性力ΔF =Δmω2r(其方向与向心加速度的方向相反).因此,单位质量力 am=fxi+fyj+fzk=g+ω2r;单位质量分力[3]:

等压面:将(1)代入等压面微分方程:fxdx +fydy+fzdz=0,即得:
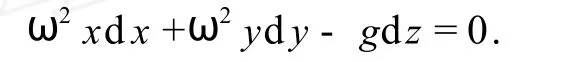
作不定积分得:
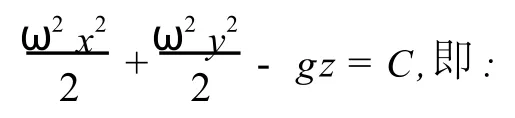

这说明等压面是绕z轴的一组回转抛物面.当r=0时z=0,可得自由表面上的积分常数C =0,故自由表面的方程式为:
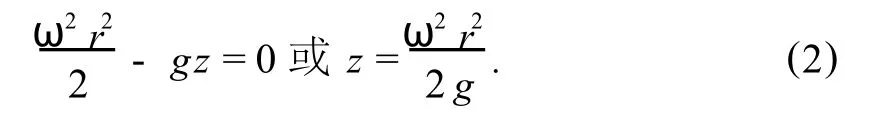
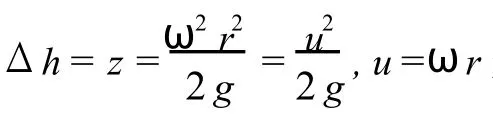

在ox y坐标平面以上的回转抛物体内的液体体积为:

这说明圆筒形容器中回转抛物体的体积恰好是高度为最大超高的圆柱形体积的一半.依据这个规律,在已知ω、R和 h(h为筒体静止时液体深度)情况下,可得液体可达最高高度为:

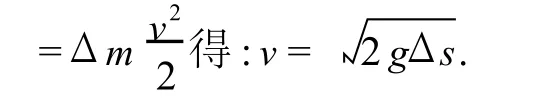
而根据如图4所示的位置关系得:

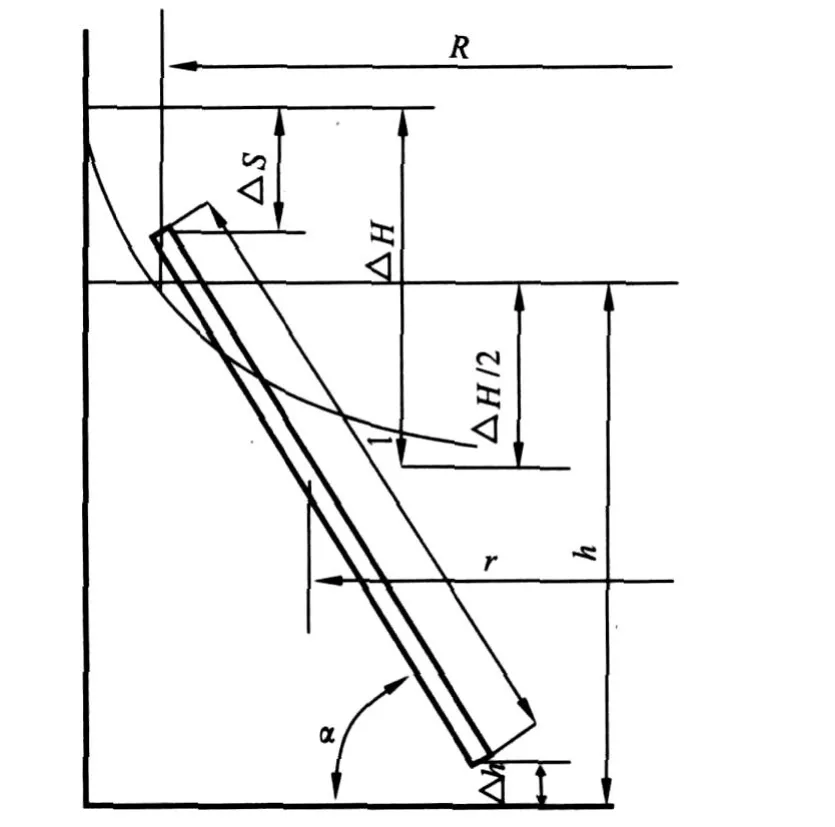
图4 简化计算尺寸位置关系Fig.4 Ubiety of size in the account
将速度分解:

单导管内液体流量:

其中,d为导管直径.
3 实验及分析
为证实文章提出的自吸叶轮流量简化计算公式的正确性,对流量进行实验测试.实验系统采用与文献[2]相同的装置.改变搅拌管张角α,测得不同张角、不同转速下的叶轮自吸排量和搅拌功率.实验结果见图5.
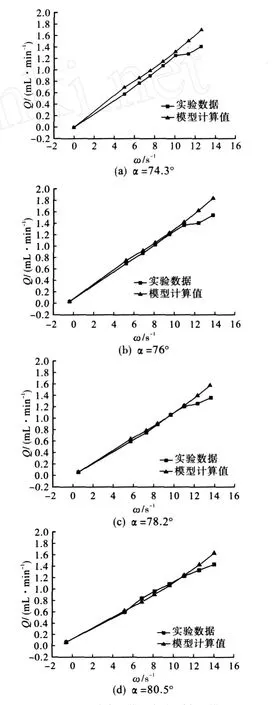
图5 理论自吸排量与实测自吸排量Fig.5 Self-suction flow rates from theoretic calculation and measurement
从图5中曲线可以看出,流量的简化计算值在低转速(ω≤12 s-1)时几乎与实验值相同,偏差在5%左右;但在较高转速范围内(ω≥12 s-1),计算值与测量值的偏差显著增大,其原因主要是简化计算中没有考虑流体排出过程中液体液位下降,以及转速提高液体在自吸管出口处的离心力远大于进口处(流体的流出效率远大于流入自吸管)等因素所致.当转速达到ω≥15 s-1时,简化计算值与实验测量值偏差在15%以上,这可能主要是液体在自吸管出口处的离心力远大于进口处所致.
4 结束语
提出一种自吸式搅拌装置的简化设计计算方法,为搅拌桨的自吸流量等性能分析提供了一种简化的计算模型.在计算中,由于忽略重力和管壁的摩擦阻力等的影响,计算所得的排出流量较实验值偏大.计算所得数据值较连续性方程推导出来的计算值更贴近实验数据,可见简化计算方法考虑了一些在连续性方程推导中忽略的因素:如自吸管的夹角,自吸管口距旋转中心的距离等因素的影响效果.由于简化计算方法主要通过静力学过渡而来,存在一些可能影响计算结果的因素的忽略.随着对自吸式搅拌装置研究的深入,考虑条件的更加细致化,对简化计算方法将是一种更深层次的检验.
[1] 罗鹏.新型化学反应器若干问题研究[D].沈阳:东北大学,2005.
[2] 罗鹏,陈富新,张俊芳.一种新型自吸式搅拌装置及其设计计算方法[J].化学工程,2006,34(6):33 -36.
[3] 张也影.流体力学[M].2版.北京:高等教育出版社,1999:50-51.

