低段“几何图形”教学的误区与对策

徐惠珍

现象反思

低年级教材中的“平面图形”或“立体图形”这类知识相对独立，老师们都喜欢把它作为公开课。听这类课的机会自然也就多，一琢磨就发现一个共性：这类新课更多地是上成了“汇报表演课”。安排了“分一分、摆一摆、数一数”等活动，热热闹闹。等活动结束了，静下心来想一想：活动仅仅只是活动，分完了就好了，摆出来了就行了。为分而分，为摆而摆，点到为止。学生并没有因为这些活动而得到更加深入的认知。和低段老师们交流，他们都认为造成这种现象的原因是：低段教学没有要求用文字概括总结出它们各自的特征(如：长方形有四条边、四个直角、对边相等且平行)。所以也就只能这样，无法深入。难道没有了规范性语言的总结与定论就无法深入去认识这些图形吗?

仔细思考，其实真正的原因在于老师看待活动的态度和对活动的定位，“活动是为了什么——是走过场的热闹汇报还是作为进一步认识的机会?”老师们应该静下心来想这些活动的真正意图是什么?活动的背后，我们所要真正追求的是什么?如果把活动作为进一步认识的平台，我们就要追求“有思维的活动”。就应该去关注活动中的“思考”，活动中的“思考”才是把认识引向深入的关键。而如何在热闹的活动中唤起学生的思考，挖掘出活动的最大效益才是我们的当务之急。

实践做法

以“如何有效利用三次活动，通过思考与交流把学生对平面图形的认识推向深入”为例，进一步阐述我上述观点。

一、分不是终点，分后的“比较”才是关键

活动一：分一分

(从体中抽象出面，对图形有了初步认识之后，可安排“分一分”这一活动)

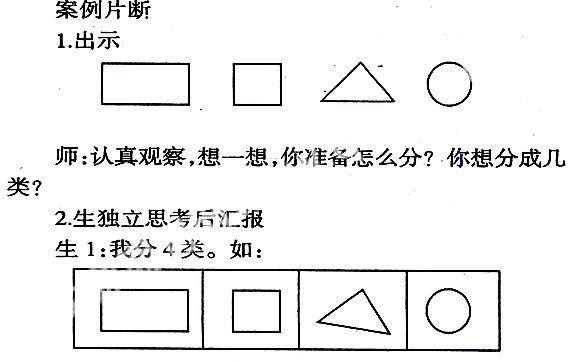
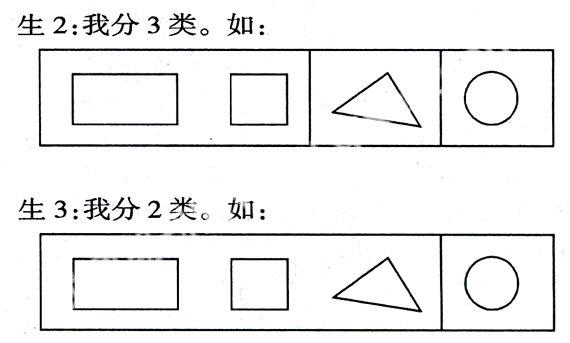
(分完后，把各种分法竖着摆放到一块进行比较)

师：请小朋友竖着观察，认真比较一下这三种分法，你又会有哪些新发现呢?(生独自观察后交流)

生1：我发现了圆总是自己一类。

生2：我发现长方形和正方形两次都分到一块了，它们长得很像。

师：为什么圆总是自己一类呢?

(生个个争先恐后)

生3：因为它没有尖尖角、圆溜溜的。只好自己一类了。

生4：把它立起来还会滚呢，其他正方形、长方形、三角形它们都不会滚。

生5：它没有直直的线，只有弯弯的线，所以它自己一类。

(生说得多好啊)

师：为什么正方形和长方形可以分为一类?它们到底相像在哪呢?

生交流后汇报：

生1：长方形和正方形它们都有4条边，都有方方的角。

生2：它们看上去方方正正的。

师：它们是完全一模一样吗?

生齐声说：不是。

师：不同在哪呢?

生1：正方形比长方形更方方正正。

生2：长方形看上去比正方形更瘦、更长，有两条边是长的，有两条边是短的。

生3：我知道正方形四条边一模一样长。

……

评析：因为要分类，学生就不得不去认真观察它们的各自“长像”。就会不由自主地从边的数量及曲直；角的数量及形状上去对比，促使学生主动去观察这四种图形的特征。然而我们课堂常常“分完为止”。其实这环节真正能把活动引向深入，更重要的是分完后对各种分法的“比较”。这种分法的比较比起“分后说为什么这样分”更易于激发说的欲望和提供说的素材。而后，通过把相似的或反差极大的图形放在一起“比一比”将进一步引发学生更加深入的思考。上述案例正因为有了分之后的“比较”，学生才有了一个与他人共鸣的机会，并有了把认识内化并不断深入的一个过程。学生那样真真切切、实实在在的、儿童化的淋漓尽致的描述，虽不是那么严谨与规范，但却是那么真实。学生这种用成人语言也代替不了的表述不正是深入认识的一种体现吗?

二、摆不是结果，摆后的“追问”才是精华

活动二：摆一摆(在分完、比较完后，摆一摆这四种平面图形)

案例片断

师：请同学们用桌上的小棒摆一摆我们今天学过的图形。

生各自主动操作。

操作完的展示：边展示边说明各自摆法。

生1：我用了三根小棒摆了一个三角形。我用了四根小棒摆了一个正方形。用了六根小棒摆了一个长方形。(经观察发现，学生们基本都是这种摆法，也许是孩子年龄特征决定了孩子的思维单纯，没想过“至少”二词的含义，师也不必多说)

师：摆一个长方形你用了六根小棒，为什么用这么多啊!用四根不行吗?

生1：用四根就变成了正方形了，两边要更长些。

师：咦!圆也是我们今天学习的图形，你怎么没有摆出来啊?

生1：(迟钝了一会儿，马上反应)：老师，你给我们的小棒是直的，我们摆不出来，圆是弯弯的线。……

评析：通过摆一摆，相当于让学生经历了“直观——抽象——直观”的过程。把刚认识的图形重新从大脑中调出来，再次直观呈现，强化孩子们对这些图形的记忆。“追问”恰恰成了把摆一摆这一活动引向深入的“着眼点”。正因为有了“追问”，才唤起了学生的认真思考，让大家有了再一次对这四种平面图形感悟和深入认识的机会。

三、变不是目的，变中的“停与不停”才是灵魂

活动三：变图形

(准备两个信封，信纸露出一部分，信封里的纸可灵活处理，长方形信纸已事先打好针孔，可根据需要撕出正方形)

案例片断：

师：请同学们来指挥老师变图形。

生请老师变出一个长方形，

师：(用力一拉)拉出一个正方形。

生：(众人附合)不算重来。

师：好!重来。这次我慢慢拉信纸，可你们要注意观察，如果是长方形，你们就要喊“停”，好吗?

师：(师慢慢拉出信纸，此时学生叫“停”的声音此起彼伏，老师用手势让学生停下)，老师真的很为难，要听谁的话呢?

生：刚才你拉出来的信纸都是长方形，如果你再继续拉可能又会变成正方形的了。

师：你怎么说等会儿会变成正方形?

生1：现在上下比左右短，如果继续拉，上下和左右就会一样长，到时又变成正方形的了。

生2：上下与左右不一样长时就是长方形，当四条边都一样长时就是正方形了。

师：哦!很有道理。这样吧!老师再拉一次，这次不喊“停”，请你们根据拉出的图形，不断说出“长方形”或“正方形”。

生：学生齐声说：长方形、长方形……正方形。

师：到正方形时，停下，问：如果再继续拉，会出现什么图形?

生(众生说)：长方形。

师：怎么又会变回长方形啦?

生1：再拉出来，上下又会比左右更长了。四条边又不一样了。

师：演示验证大家的猜想，并再次推信纸，要求学生还是说出“长方形、长方形……正方形、长方形……”。

师：在刚才拉、推的活动中，你们有什么发现?

生：有时是长方形，有时是正方形。长方形可以变成正方形，正方形可以变成长方形。

师：也就是说长方形和正方形可以互相转化，什么情况下是长方形?什么情况下是正方形?

生1：如果长方形的四条边都相等时，就成为正方形。

生2：正方形的四条边不相等时就成为长方形。

评析：在“变图形”活动中，变出结果不是我们的终点，通过变图形的活动让学生的认识再次提升才是我们所追求的。而活动中的“停与不停”就成了活动的“灵魂”。因为有意的“停与不停”才会有学生思考、想象的空间，才能在变化中感悟到图形间的相关转换关系。使学生的认识在活动中再次得到提升。

有了“分”完之后的“比较”；“摆”中的“追问”；“变”中的“停与不停”，就把活动有效利用起来，让“思考”贯穿于活动全程，真正把认识推向了深入。上述片断中学生们那些淋漓尽致的表述，又何愁认识不深人，又怎么可能只是停留于已有经验的“辨认”上?仔细想想，无论是上述的教学、还是其他知识的教与学，我们在设计活动时不妨多反问自己：在活动的背后，我的目的何在?我要达到什么目标?认清目标，让学生的大脑在活动中动起来，想办法让活动真正有效起来，挖掘其最大价值，为我们的教与学服务。

(责任编辑：李雪虹)