可减小跟踪误差的月球探测车协调驱动模糊自适应控制*

孙多青，马晓英，杨晓静，俞百印，邵香媛

（1.河北科技师范学院数理系，秦皇岛066004；2.河北科技师范学院数学与系统科学研究所，秦皇岛066004；3.河北科技师范学院图书馆，秦皇岛066004）

可减小跟踪误差的月球探测车协调驱动模糊自适应控制*

孙多青1，2，马晓英2，3，杨晓静1，俞百印1，邵香媛1

（1.河北科技师范学院数理系，秦皇岛066004；2.河北科技师范学院数学与系统科学研究所，秦皇岛066004；3.河北科技师范学院图书馆，秦皇岛066004）

针对六轮月球探测车的协调驱动控制问题，提出一种间接模糊自适应控制设计方案。基于Lyapunov方法，证明所设计的控制方案不但能使跟踪误差收敛到原点的小邻域内，而且通过适当增大设计参数的值，可减小跟踪误差，从而提高控制精度。通过对月球探测车的协调驱动控制的仿真研究验证了此方法的有效性。

月球探测车；自适应控制；模糊控制；精度；非线性系统

1 引 言

月球探测车（也称为月球漫游车或月球漫游机器人）是探月工程中的一个重要研究课题。进入21世纪，中国已有许多机构对各种轮式月球探测车进行分析和设计研究[1-2]。在各种新型的探测车中，六轮摇臂悬挂式车体结构的综合性能较好，但其运动学建模与控制比较复杂[3]。文献[4]具体分析了探测车在松软月表土壤上的动力学建模问题，提出了相应的简化模型，并对探测车的协调驱动控制问题进行了初步研究。然而，对于在月表复杂环境下运行的探测车来说，探测车精确的驱动动力学模型是很难得到的，需要研究模型不确知情况下的驱动控制问题[5]。这一问题实际上属于不确定非线性多输入多输出系统的控制问题。近年来，利用模糊系统等工具实现自适应控制的方法已成为非线性自适应控制的一个研究热点，并取得了许多成果[6-8]。模糊逻辑控制是处理模型不确定问题的一种有效方法，文献[5]对非线性多输入多输出（MIMO）系统，提出一种组合自适应模糊控制方法，将该方法应用于月球探测车的驱动控制中，并进行仿真研究。然而文中并未考虑如何减小逼近误差来提高控制精度，这也是模糊控制领域中的基本问题之一。本文借鉴文献[9-10]中的方法，针对六轮月球探测车的协调驱动控制问题设计了间接自适应模糊控制器，不但证明设计的控制方案可保证闭环系统稳定，还证明了适当增大设计参数的值，可减小跟踪误差。

2 问题描述

月球探测车采用六轮摇臂悬挂式底盘结构，驱动系统的工作方式为六轮独立驱动，前后四轮协调转向，驱动系统的结构和组成原理参见文献[3]。月球探测车在松软土壤上行驶时的驱动系统动力学方程为[4-5]

式中，x=[λ1λ3λ5]T为状态向量（车轮的滑转率），u=[T1T3T5]T为控制输入（车轮驱动力矩），f和g的表达式分别为

其中，Fni为车轮i在竖直方向上的负载；v为车速；m0为整车质量；r为车轮半径；IW为车轮转动惯量；a0j，a1j，e0i，e1i为常数[4]。

由此可见，月球探测车的驱动系统是一类具有对角型输入的非线性MIMO系统。在以下的设计过程中，可以将式（1）写成分量的形式，并考虑干扰的影响，则有

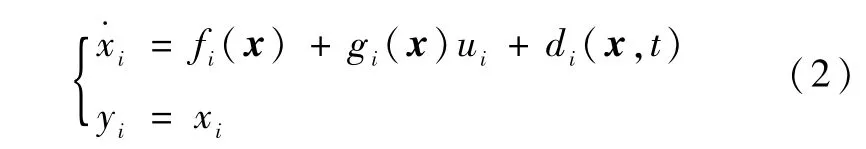
假设系统满足下列条件：

假设1.存在已知的正的连续函数（x），（x）和gLi（x），使得对处于某一区域Uc∈R3内的x，有：

假设2为已知正常数。

只要车速v＞0，且知道v或其它参数的变化范围，系统即可满足假设（1），参见仿真部分。

控制任务：针对fi（x）和gi（x）未知的情形，利用模糊逻辑系统设计自适应控制律，使系统输出yi跟踪给定的期望值yri，满足（Ⅰ）所有信号及参数估计有界；（Ⅱ）跟踪误差ei≜yri-yi=xri-xi收敛到原点的小邻域内，且通过适当调整设计参数可使跟踪误差减小。

3 自适应模糊控制器的设计

模糊规则库是由具有如下形式的若干模糊“如果-则”规则组成的：

R（l）：如果x1为，…，且xn为，则y为，l=1，2，…，M。

若采用模糊单值产生器，依据乘积推理规则和加权平均去模糊化方法，则模糊逻辑系统的输出为

在fi（x），gi（x）未知的情况下，由万能逼近定理知：可由构造的模糊逻辑系统来逼近fi（x），gi（x）：

定义如下参数范围：

其中，Mfi，Mgi和εi都是设计者取定的正数，根据对象的初步特性的分析以及状态和控制输入的约束条件可以得到fi（x）和gi（x）的大致范围，从而可以得到可调参数的估计范围，依据这些估计范围即可初步确定Mfi、Mgi和εi的选取范围。≥εi用来保证（x|θgi）＞0，与假设（2）中gi（x）＞0相一致。

取控制律

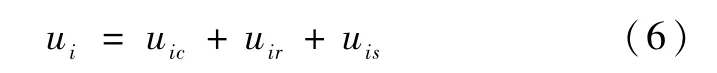
式中，uic为等效控制项，uir为补偿控制项，uis为监督控制项。取

可以把补偿控制uir和监督控制uis选为如下的形式：

式中，αi，βi＞0为设计参数，且αi的选取满足αi＜ki。

之上界Mx而选定的正常数。

将式（6）和（7）代入式（2）得误差方程

由式（8）知，eigiuir＞0，于是，当Vei＞时，由式（9）和（11）可知：因此，可以保证Vei≤，所以ei有界。

下面给出参数向量的自适应律。定义

定义最小逼近误差为

参数自适应调节律可设计如下：

1）采用下列自适应律来调节参数向量θfi

其中，投影算子P｛*｝定义为

2）采用下列自适应律来调节参数向量θgi

当θgi的某一分量时，采用

否则，采用

4 稳定性分析

在以上自适应模糊控制器的设计过程中，保证了闭环系统的稳定性，关于稳定性的结论可以用以下的定理来给出。

定理1.对控制对象（2），如果满足假设1和2，控制律取式（6），参数调节律为式（13）～（15），则有

（ⅰ）‖θfi‖≤Mfi，‖θgi‖≤Mgi，θgi的所有分量≥εi，

并且

（ⅱ）跟踪误差收敛到原点的小邻域内，且通过适当增大设计参数的值，可使跟踪误差减小。

证明.1）结论（ⅰ）的证明与文献[11]类似，此处从略。

2）考虑如下的Lyapunov函数：

对Vi求导得

将式（12）～（15）代入上式，经过整理可得

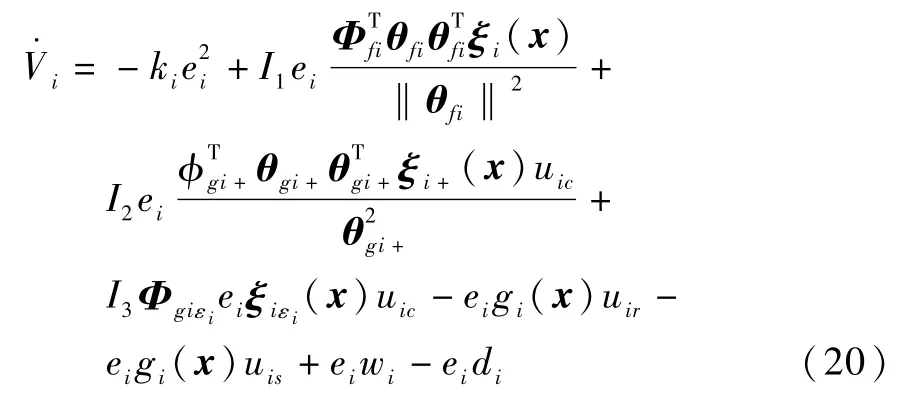
当式（13）中第一行（或第二行）成立时，I1=0（或I1=1）；当式（14）中第一行（或第二行）成立时，I2=0（或I2=1）；当式（15）中第一行（或第二行）成立时，I3=0（或I3=1）。另外，θgi+表示θgi中所有满足＞εi的分量构成的向量，θgiεi表示θgi中所有=εi的分量构成的向量；Φgi+=θgi+-，Φgiεi=θgiεi-；ξi+（x）（ξiεi（x））表示ξi（x）中对应于θgi+（θgiεi）的向量。

由文献[11]知：式（20）中带有I1，I2和I3的项均为非正，因此可得

由式（9）和假设（2）中gi（x）＞0可得eigi（x）uis≥0，故上式可进一步简化为

根据uir的表达式（8）可知-eigi（x）uir=代入式（21），并结合假设（2）及αi＜ki可得

因为xi，θfi，θgi，uic均有界，故wi有界，又已知di有界，于是可设|wi|+|di|≤Wid，从而

由于θfi，θgi均有界，故可设|Φfi|≤Wfi，|Φgi|≤Wgi，记，则由Vi和Vi0的定义和式（22）可得[9]

从而

据此

其中，C0是与时间t无关的常数。令t→+∞，并注意到α＞0，故V≤V0（t→+∞），进而→+∞）。

于是，可知ei（t）收敛到原点的小邻域内，且适当增大βi的值，可使V0的值减小，因此可使|ei|减小，即实现了控制目标（Ⅱ）。因此定理结论成立。证毕。

5 仿真实验

现在采用上节给出的控制方案，对月球探测车的驱动控制问题进行仿真研究。对象的实际动力学方程如式（1）。控制目标为：通过对各个车轮驱动电机输出力矩的控制，使得各个车轮的滑转率λi跟踪给定的期望值λri。因为λi=0.3左右时，驱动效率最高[4]，故本文滑转率的目标值取为λri=0.3。系统的各个参数值如下[5]：整车质量m0=60kg，车轮转动惯量IW=3.38×102kg·m2，Fn=[26 26 48]TN。由文献[4]可知当Fnj=26N时，a0j=0.449，a1j=-0.022，e0i=0.516，e1i=0.083；当Fnj=48N时，a0j=0.443，a1j=-0.025，e0j=0.449，e1i=0.119。加于3个车轮上的摄动及干扰为

在仿真中，模糊逻辑系统的隶属函数取为

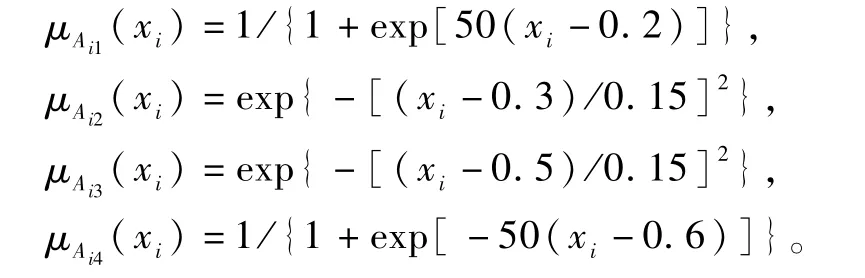
取ki=4，αfi=0.1，γf1=γf3=γf5=1，γg1=γg3=γg5=1。先取β1=β3=50，β5=100，仿真结果见图1中的虚线；再取β1=β3=150，β5=300，仿真结果见图中的实线。由图可见，增大βi确实可使误差减小。与文献[5]相比缩短了稳态时间。

6 结 论

对月球探测车的驱动控制问题提出了一种间接自适应模糊控制方案，根据李亚普诺夫理论证明了所给出的控制方案不但能保证闭环系统稳定，跟踪误差收敛到原点的小邻域，而且通过适当增大设计参数的值，可使跟踪误差减小，从而提高了控制精度。仿真实验验证了该方法的有效性。

图1 仿真结果

[1] 刘方湖，马培荪，曹志奎等.五轮铰接式月球机器人的运动学建模[J].机器人，2001，23（6）：481-485

[2] 蔡则苏，洪炳镕，吕德生.HIT-1型月球车的运动学分析[J].哈尔滨工业大学学报，2003，35（9）：1098-1101

[3] 王佐伟，梁斌，吴宏鑫.六轮月球探测车运动学建模与分析[J].宇航学报，2003，24（5）：456-462[4] 王佐伟，吴宏鑫，梁斌.月球探测车动力学建模与协调驱动控制[C].第22届中国控制会议，武汉：武汉理工大学出版社，2003，554-558

[5] 王佐伟，吴宏鑫.一种组合自适应模糊控制方法及其在月球探测车上的运用[J].宇航学报，2005，26（1）：1-6

[6] RAUl Ordonez，PASSINO K M.Stable multi-input multi-output adaptive fuzzy/neural control[J].IEEE Transactions on Fuzzy Systems，1999，7（3）：345-353

[7] CHANG Y C.Robust tracking control for nonlinear M IMO systems via fuzzy approaches[J].Automatica，2000，36（6）：1535-1545

[8] ZHANG Huaguang，ZHANG M ingjun.Robust tracking control for nonlinear M IMO systems via fuzzy approaches[J].Progress in Natural Science，2006，16（10）：1098-1105

[9] 孙多青，霍伟，杨枭.含模型不确定性移动机器人路径跟踪的分层模糊控制[J].控制理论与应用，2004，21（4）：489-494

[10] 孙多青，马晓英，俞百印等.带有鲁棒控制项的MIMO非线性系统的模糊控制[J].浙江大学学报（工学版），2007，41（10），1620-1624

[11] 王立新.自适应模糊系统与控制¯设计与稳定性分析[M].北京：国防工业出版社，1995：245-246

Fuzzy Adaptive Concerted Driving Control for Lunar Rover w ith Reduced Tracking Errors

SUN Duoqing1，2，MA Xiaoying2，3，YANG Xiaojing1，YU Baiyin1，SHAO Xiangyuan1
（1.Department of Mathematics and Physics，Hebei Normal University of Science and Technology，Qinhuangdao 066004，China；2.Institute of Mathematics and Systems Science，Hebei Normal University of Science and Technology，Qinhuangdao 066004，China；3.Library，Hebei Normal University of Science and Technology，Qinhuangdao 066004，China）

A novel indirect adaptive fuzzy control scheme is proposed for the concerted driving control of six-wheel lunar rover.Based on the Lyapunov theory，it is proven that the designed scheme not only makes the tracking errors converge to a small neighborhood of the origin，but also reduces the tracking errors through increasing the value of designed parameters，and the control accuracy is improved.Simulation results on the concerted driving control of lunar rover verify the efficiency of the approach proposed.

lunar rover；adaptive control；fuzzy control；accuracy；nonlinear system

TP273；O231

A

1674-1579（2008）05-0012-05

*河北科技师范学院博士基金项目（2006D003），国家自然科学基金资助项目（60874055）.

2008-06-05

孙多青（1962-），男，河北人，博士后，教授，研究方向为智能控制、运筹学等（e-mail：sun-duoqing@126.com）。