对汽车功率恒定启动问题的深入研究

广东 任富华

定与不定，一探便知。

一、问题引入

【例1】(2015年全国卷Ⅱ)一汽车在平直公路上行驶。从某时刻开始计时，发动机的功率P随时间t的变化如图所示。假定汽车所受阻力的大小f恒定不变。下列描述该汽车的速度v随时间t变化的图线中，可能正确的是

( )

A

B

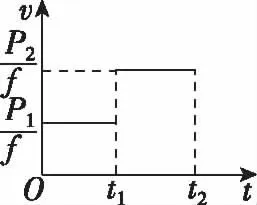
C

D

物理是一门以实验为基础的学科，实验往往伴随着数据。在教学中，一个物理过程或现象都能够呈现具体的数据，也更能让学生理解，于是就出现了例2。

【例2】质量m=20 kg的探测车以额定功率从静止启动，经过时间t0=22 s速度达到最大值vm=10 m/s，已知探测车始终沿直线运动，探测车在运动过程中受到的阻力为自身重力的0.05，取重力加速度g=10 m/s2，求：

(1)探测车的额定功率；

(2)探测车从启动至速度达到最大值的过程中的位移大小。

本题主要考查功率和动能定理的综合应用，简单解析如下：

(1)由P0=Fv知，当F=f=0.05mg=10 N时，速度最大，可得额定功率P0=100 W。

以上每一个步骤都有理有据，解答过程没有问题。笔者质疑的是22 s达到最大速度这个“事实”，可不可以说经过10 s或者100 s速度达到最大值？探测车功率恒定，所受阻力恒定，探测车运动情况应该是唯一的，一个时刻对应唯一的速度。接着出现两个问题：探测车能不能达到最大速度？探测车经过多长时间达到最大速度？

二、问题分析

物理题目往往都是将真实生活或实验情景抽象化、理想化，而抽象化、理想化本身就是物理学所要求的一种思维方式，并不违背科学性。例2中探测车的最大速度为10 m/s，探测车运动过程中受到的阻力为自身重力的0.05，这样的假设是合理的。

假设探测车可以达到最大速度10 m/s，怎么近似研究全过程的运动时间呢？我们将整个加速运动过程分成若干个速度增加量均为0.2 m/s的过程，将每一个过程当作匀加速直线运动，探测车的运动时间会怎样呢？

研究探测车的两个运动过程，过程1：速度从9.6 m/s增加到9.8 m/s；过程2：速度从9.8 m/s增加到10 m/s。

对于过程1，当速度v1=9.6 m/s时，牵引力

此时探测车的加速度

此过程运动的时间

对于过程2，速度v2=9.8 m/s时，牵引力

此时探测车的加速度

此过程运动的时间

图1

实际上，探测车在上面两个过程的运动时间要大于解得的时间。以过程1为例，速度变化大致图象如图1 所示，实际运动时间为t1′，近似处理后运动时间为t1，由图1可知t1′>t1。所以，上面两个过程运动的总时间t′>(t1+t2)=29.2 s。

经过以上分析，我们至少可以得出一个结论：例2中“经t0=22 s速度达到最大值vm=10 m/s”是不科学的，“t0=22 s”是编题者随意设定的时间。那到底探测车能否达到最大速度？如果能，需要多长时间？要圆满回答以上问题，需要用到高等数学知识——微积分。

三、问题解答

探测车从静止保持功率恒定启动，t=0时，速度v0=0。设t时刻探测车的速度为v，此时，牵引力

根据加速度的定义可知t时刻的加速度

根据牛顿第二定律，可知加速度

由以上3式可得

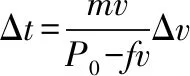
将④式变式可得

将⑤式积分，结合t=0时，v0=0可得

将例2中m=20 kg，f=10 N，P0=100 W代入⑥式，可得

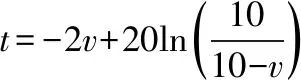
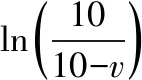
利用几何画板，得到v随t变化的函数图象如图2所示，图象趋近于直线v=10 m/s，但不会相交。

图2