电推进系统压力调节单元的建模和分析
苟浩亮,潘海林
(北京控制工程研究所,北京100190)
电推进系统压力调节单元的建模和分析
苟浩亮,潘海林
(北京控制工程研究所,北京100190)
建立了电推进系统压力调节单元的数学模型,利用Matlab/Simulink软件分析几个重要参数对系统的影响。仿真结果表明,采用bang-bang控制策略具有较高的控制精度,可满足系统的指标要求。
电推进系统;压力调节;bang-bang控制
1 引 言
近年来,以氙气为工质的电推进系统由于其具有高比冲的优势而迅速发展,尤其是霍尔和离子推进系统备受各航天大国青睐,用于静止轨道卫星平台执行南北位置保持、姿态控制(动量轮卸载)和轨道控制,甚至同步轨道转移等任务,此外电推进系统可以完成常规推进系统无法完成的任务,如深空探测、星际旅行等需要大ΔV的任务以及卫星、微小卫星的精确姿态控制和卫星星座组网控制等任务。
氙离子推进系统需要一套单独的供给系统,进行高精度的压力调节和推进剂微流量精确控制,以确保推力器稳定工作。氙气供给系统(XFS)按其功能可以分为3个部分:存储单元、压力调节单元和流量控制单元。本文首先建立以开关电磁阀和稳压罐为核心部件的压力调节单元的理论模型,然后提出bang-bang控制策略,最后进行仿真分析。
2 压力调节单元简介
压力调节单元的结构组成如图1所示,系统主要由高压压力传感器、高压自锁阀、电磁阀、稳压罐、低压压力传感器、低压自锁阀、管线和接头以及控制器组成。

图1 压力调节单元的组成
压力调节单元在XFS中位于高压气瓶与流量控制单元之间。工作时,首先高压自锁阀打开,使上游高压氙气无阻碍地到达电磁阀的进气口,然后根据系统的减压控制要求,由控制器控制电磁阀组的开启和关闭状态,从而控制高压氙气在稳压罐中的减压过程和减压指标,以满足下游流量控制单元对低压气源的要求。
3 氙气的物理性质简介
氙气位于元素周期表最后一列,属于惰性气体族,由于其单原子分子结构,有较大的相对分子质量(131.3)及较低的电离势能这一特点,故被选作电推进系统的推进剂。此外,氙气本身的一些特点也是卫星电推进系统应用所必须考虑的,例如其临界压力Pc=5.84MPa,临界温度Tc=289.85K,其密度随压力和温度的变化曲线如图2所示。
从图2可以看出,当储存压力高于5.84MPa时,密度随压力变化的等温曲线相当陡峭,十分接近289.85K的等温线,极小的温度变化将会引起较大的密度/压力漂移。为了避免出现两相状态,即由温度传感器的误差、系统节流等引起的两相状态,必须保证供给系统的工作温度至少维持在293.15K以上。
再者,若在实际中把氙气作为理想气体处理将带来极大的偏差,本文引入压缩因子Z对理想气体状态方程进行修正,得到Pν=ZRT(ν为比容),对氙气的各个状态参数进行计算,其中压缩因子是压力和温度的函数,即Z=f(P,T)。图3为根据NIST提供的数据拟合的氙气在293.15K时压缩因子随压力的变化曲线。

图2 氙气密度随压力变化曲线

图3 氙气在293.15K时压缩因子随压力的变化曲线
4 压力调节单元的数学模型
如图1所示,记气瓶中气体参数(压力、容积、温度和质量)为P1,V1,T1和M1;容腔中气体参数为P2,V2,T2和M2;稳压罐中气体参数为P3,V3,T3和M3;电磁阀流量分别记为qm1,qm2;稳压罐输出流量记作qm0。根据系统工作原理建立数学模型,由于氙气供给系统要求工作在293.15K附近且在压力调节单元下游的流量控制单元进行精确的微流量控制,建立数学模型时假设:
1)高压气瓶放气过程、容腔及稳压罐的充、放气过程进行得非常缓慢,系统与外界能充分地进行热交换(由星上热控系统实现),均可近似视为等温过程,即T=293.15K;
2)各个容积内压力场均匀分布;
3)不计引力场作用;
4)内、外漏忽略不计。
4.1 流量方程
采用流量系数及压缩因子对等熵喷管流量方程加以修正,得出实际气体流经电磁阀的流量

式中,

式中,Pu,Pd分别为电磁阀上下游的气体压力,Pcr为临界压力比,Cd为电磁阀的流量系数,A为阀口面积,Tu为上游气体温度,R为气体常数,Z为气体压缩因子,k为气体绝热指数。
4.2 连续方程
由于气瓶体积V1,容腔V2以及稳压罐的体积V3皆为定值,且工作过程为等温过程。
气瓶连续方程:
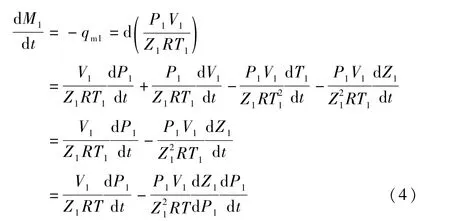
容腔连续方程:分为充气和放气两个工作过程。
1)充气过程:

2)放气过程:
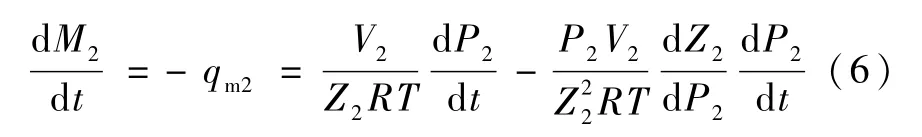
稳压罐连续方程:分为同时充、放气和只有放气两个工作过程,因为气容工作压力小于1MPa,故
可按理想气体处理,压缩因子Z3=1。
1)同时充、放气过程:

2)仅放气过程:
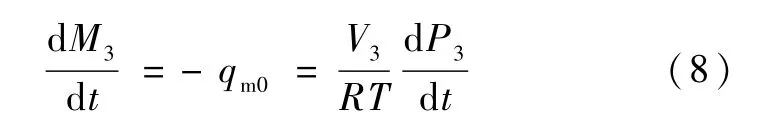
4.3 能量方程
由于假设气瓶放气过程及稳压罐充、放气过程为等温过程,由热力学第一定律有[1]

式中,Q为充放气过程中与外界交换的热量。
5 压力调节单元的bang-bang控制
Bang-bang控制是一种时间最优控制,亦称最速控制,是一种工业上常见的最优控制[2-3]。控制回路如图4所示。
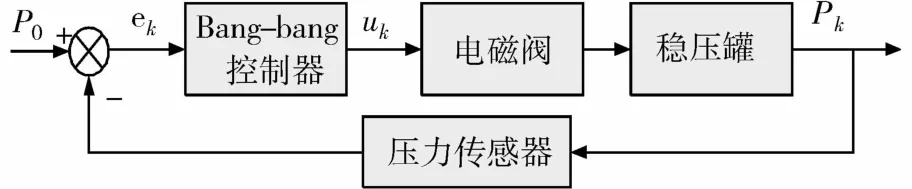
图4 bang-bang控制回路
Bang-bang控制算法如下:

式中,Pk为第k次采样的压力值,P0为气容的工作点压力设定值,e(k)为稳压罐输出压力与设定工作压力的偏差,u(k)为第k次采样后控制器的输出值。其工作过程的控制原理如图5所示[4-5]。

图5 bang-bang压力调节单元的工作过程示意图
当低压压力传感器检测到稳压罐的输出压力低于工作压力的设定值时,由控制器发出指令使电磁阀组按以下方式工作:
1)上游电磁阀打开;
2)气瓶中的高压氙气开始向压力调节单元两个电磁阀之间的小容腔充气;
3)经过t1后,上游电磁阀关闭;
4)经过t2后,下游电磁阀打开,小容腔中的氙气开始流入稳压罐中,稳压罐内压力逐渐升高;
5)经过t3后,下游电磁阀关闭,至此电磁阀全部关闭,一个工作周期结束,令T=t1+t2+t3,称为一个减压工作周期。
根据系统减压和稳压的指标要求,通过调节控制电磁阀组工作周期的循环次数及各个电磁阀的开启和关闭时间,可以控制稳压罐输出压力。是否进入下一个工作周期,取决于稳压罐的输出压力是否低于设定的工作压力。
压力调节单元为一个非线性的数学模型,需要求解非线性方程组。计算机及应用数学软件的发展为我们提供了便利之处,Matlab/Simulink工具箱[6]提供了求解和模拟非线性系统动态特性的便利工具。为此,利用Simulink的封装子系统技术建立了bang-bang电子压力调节单元的仿真模型。
6 仿真结果及分析
设定压力调节单元的仿真参数为:系统工作温度T1=T2=T3=293.15K,气瓶中气体压力P1=8 MPa,容腔容积V2=0.5m L,电磁阀阀口直径d=0.2mm,稳压罐容积V3=3L,氙气气体常数R=63.3J/(kg·K),气体绝热系数k=1.67,电磁阀流量系数Cd=0.6,稳压罐设定工作压力P0=0.2MPa,下游输出流量Qmo=2.63mg/s,一个减压工作周T=1.5s(t1=0.5s,t2=0.2s,t3=0.8s)。利用建立的仿真模型,研究主要工作参数对系统减压性能的影响,结果如下:
1)气瓶压力变化对系统减压性能的影响,仿真结果见图6;

图6 气瓶压力对系统减压性能的影响
2)电磁阀间容腔容积对系统减压性能的影响,仿真结果见图7;
3)电磁阀口直径对系统减压性能的影响,仿真结果见图8;

图7 容腔容积对系统减压性能的影响
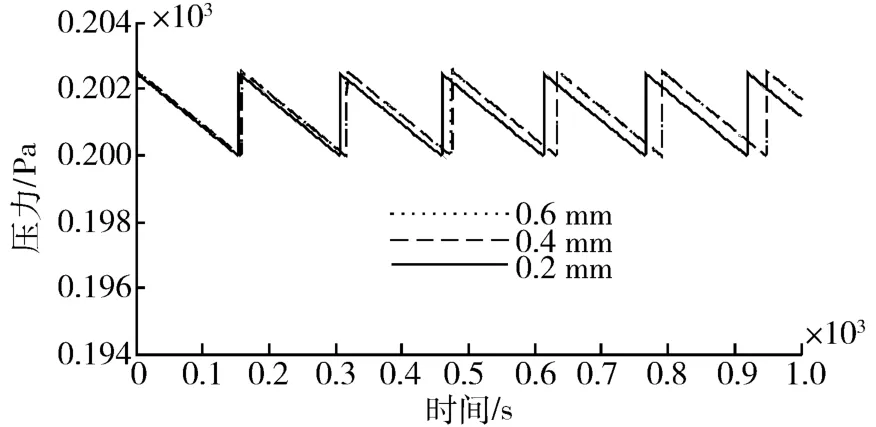
图8 电磁阀口直径对系统减压性能的影响
4)稳压罐容积对系统减压性能的影响,仿真结果见图9。

图9 稳压罐容积对系统减压性能的影响
通过以上仿真可见,系统的压力控制精度随气瓶压力的减小而增加;随阀间容腔容积的减小而增加;随阀口直径的增加,系统压力调节精度有所下降,但这种影响不大;稳压罐容积越大,系统的压力调节精度越高。此外,利用电磁阀工作在bang-bang模式下的分步开关控制方式,在压力调节过程中,电磁阀大多数时间处于关闭状态,并且不存在两个电磁阀同时开启的状态,充分利用电磁阀阀间的小容腔每次转移极少量高压气体为下游的稳压气容增压,使气容压力只能以极为有限的幅度增长,有效地避免了气瓶中的高压气体与稳压罐中低压气体之间的直接流通,很大程度上消除了由于系统硬件和软件等多方面原因产生的迟滞而造成电磁阀未能及时严格关闭,引起额外的高压气体进入稳压罐产生一定的压力过冲现象,该特性对于卫星电推进系统是至关重要的。
7 结 论
本文建立了电推进氙气供给系统压力调节单元的数学模型,并利用Matlab/Simulink动态仿真工具箱进行了数值仿真。Bang-bang控制相对于其它控制方法简单、灵活、可靠、控制精度较高,理论上能满足电推进供给系统的调压精度要求(≤3%),实际系统需考虑环境温度和测量精度等因素,如气瓶的放气过程、容腔及稳压罐的充、放气过程实际上介于绝热过程和等温过程之间,是一个多变过程,这会使得压力调节单元中稳压罐相邻的充气时间间隔相对于仿真结果有所减小;再者,实际系统的调压精度需综合考虑压力和温度传感器等的测量精度,进而优化系统结构和工作参数以使其输出压力满足指标要求,因此,关于实际系统的具体性能还有待于后续工程的进一步验证。此外,采用bang-bang控制的压力调节装置与传统的机械减压器相比,其输出压力还可通过地面遥控方式或者卫星自主程序进行在轨压力重设,从而更适用于变推力电推进系统,最后该方法经过适当的修改亦适用于常规化学推进系统的气体压力调节。
[1] 沈维道,郑佩芝,蒋淡安.工程热力学[M].北京:高等教育出版社,1983
[2] 贾光政,王选银,刘昊,吴根茂.高压气体体积减压系统的bang-bang控制研究[J].液压与气动,2004,(5):38-40
[3] 吴麒.自动控制原理(下册)[M].北京:清华大学出版社,1992
[4] Christophe R,Frederic M.Robust pressure regulation system for the SMART-1 electric propulsion sub-system[C].The 40thAIAA/AMSE/SAE/ASEE Joint Propulsion Conference and Exhibit,Fort Lauderdale,Florida,July 11-14,2004
[5] Gani B,Carl E.Post-launch performance characterization of the xenon feed system on deep space one[C].The 35thAIAA/AMSE/SAE/ASEE Joint Propulsion Conference and Exhibit,Los Angeles,CA,June 20-24,2004
[6] 黄永安,马路,刘惠敏.MATLAB 7.0/Simulink 6.0建模仿真开发与高级工程应用[M].北京:清华大学出版社,2005
Modeling and Analysis of Pressure Regulation Unit for Electric Propu lsion System
GOU Haoliang,PAN Hailin
(Beijing Institute of Control Engineering,Beijing 100190,China)
A mathematic model of the pressure regulation unit for electric propulsion system is established.Based on the software named Matlab/Simulink,the influence of several important parameters on the system is analyzed.The simulation results show that by app lying the bang-bang control,high accuracy and performance can be expected.
electric propulsion system;pressure regulation;bang-bang control
V43
A
1674-1579(2008)05-0049-04
2008-07-24
苟浩亮(1983-),男,陕西人,硕士研究生,研究方向为航天器推进技术(e-mail:ghaoliang@sina.com.cn)。

