基于LQR的小卫星磁姿态控制设计

郭延宁，李传江，马广富

（哈尔滨工业大学控制科学与工程系，哈尔滨150001）

基于LQR的小卫星磁姿态控制设计

郭延宁，李传江，马广富

（哈尔滨工业大学控制科学与工程系，哈尔滨150001）

研究仅采用磁力矩器作为执行机构的近地小卫星姿态控制问题。通过对刚体卫星的非线性动力学和运动学方程在平衡点处进行线性化处理，得到一个线性周期时变系统，应用线性二次最优调节器理论设计出最优磁矩控制律。最后针对某小卫星进行了仿真验证，结果表明所设计的最优控制律可以很好地完成三轴姿态稳定任务。

小卫星；姿态控制；LQR；磁控制

1 引 言

小卫星具备更快、更好和更省等优点，近年来其研究受到世界各国的高度重视，成为航天发展的一个重要方向。而磁力矩器具有结构简单、质量轻和功耗低等特性，直接使用磁力矩器对小卫星进行姿态控制也成为当前的研究热点[1]。

国内外很多文献都涉及了卫星姿态控制器的设计，其中大多数都是采用飞轮或喷气推力器作为执行机构完成三轴姿态控制，而使用磁力矩器仅是为了消除章动或给飞轮去饱和，很少单独使用[2-3]。这主要是因为磁控系统只能在垂直本地地磁场的方向产生控制力矩，在任意时刻只有两轴可控，所以导致对仅利用磁力矩器的姿态控制系统的研究进展相对缓慢。直到最近十几年，随着周期系统控制在各个领域的成功应用，小卫星的磁姿态控制才引起人们越来越多的关注。

由文献[4]可知，LQR控制、PID控制、模型预测控制、神经网络和滑模控制等理论都已逐步应用到卫星磁姿态控制器的设计中。文献[5]通过分析周期Riccati方程解的性质，利用牛顿迭代法求解微分Riccati方程，设计了磁控近地小卫星的周期时变控制器。文献[6]从傅立叶级数展开的角度去分析并求解微分Riccati方程，设计的控制律同样能发挥较好的性能。但由于两者在建模时没有考虑磁力矩产生的方向性约束，使得设计的控制律并非真正最优，有待进一步改进。

本文主要针对磁控制力矩产生的方向性约束设计基于LQR理论的状态控制律，从而实现真正意义上的最优控制。近地小卫星姿态控制系统框图如图1所示。

图1 卫星姿态控制系统

2 卫星运动学与动力学模型

刚体卫星的运动学和动力学方程为[7]

沿星体坐标系的三轴分别安装一个磁力矩器作为执行机构，产生的控制力矩为

式中，M∈R3为三轴磁矩，B=[BxByBz]T为星体坐标系中的本地地磁场强度矢量。

由图2可以看出，磁力矩器只能在与本地地磁场垂直的方向上产生控制力矩。根据磁力矩器的这种欠驱动的本质特点，要使磁力矩器发挥最大的能量（即产生最大的磁控力矩uc），需引入如下映射

图2 磁力矩与本地磁场关系图

3 LQR控制律设计

对式（4）所示的线性周期时变系统定义如下性能指标：

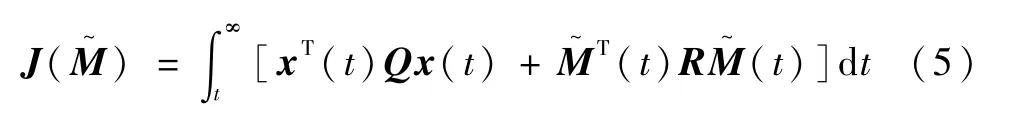
式中，Q为Q=QT∈R6×6的半正定加权矩阵，表示系统在运动过程中的动态跟踪误差总度量；R为R=RT∈R3×3的正定加权矩阵，表示消耗的能量总度量。易判断系统可控，根据最优控制理论，系统存在如下唯一的无限时间时变状态调节器

式中，P（t）=P（t）T∈R6×6为时变正定矩阵且是如下微分Riccati方程的解

该微分Riccati方程为非线性微分方程，通常情况下，由于变量之间相互耦合很难求得解析解，一般都需要由计算机求出其数值解，且计算量非常大。

由文献[5]可知，式（7）所示的周期Riccati方程的解为周期性的，所以可以离线求得该方程的周期解，将得到的状态反馈增益存储到星载计算机中，从而实现线性周期时变系统（4）的最优控制。

鉴于上述分析，由于地磁场变化缓慢，可以将微分Riccati方程分段离散化处理，在每一段时刻内将系统近似看作定常系统，即首先将其转化为近似的代数Riccati方程，然后在卫星运行的轨道周期T内对其进行计算，可得最终解Pinf（t），其分别经过周期内离散求解代数Riccati方程得到P∞（t）和对P∞（t）周期延拓得到

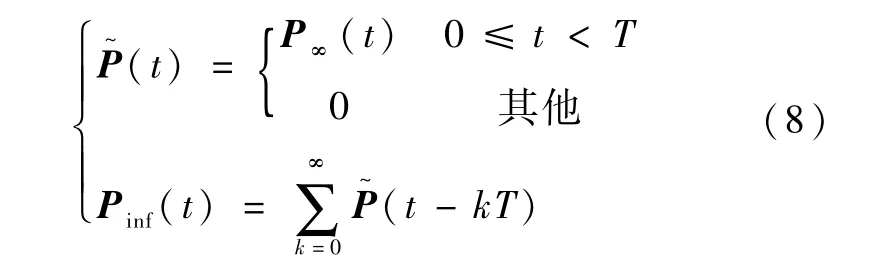
最终可得系统的LQR无限时间状态调节器为

4 仿真验证

在Matlab/Simulink环境下对某近地极轨小卫星进行仿真研究，验证本文提出的LQR时变反馈控制律。它采用的地磁参考场为IGRF2000模型，卫星参数选取如表1所示。

表1 卫星仿真参数

通过分段求解方程（7）可得系统的状态反馈增益，采用式（8）设计的LQR反馈控制律，分别对干扰力矩为ud和3ud的情形进行仿真，仿真结果如图3-6所示。图3和图4分别给出了卫星在干扰力矩为ud情况下的qbo和ωbo变化曲线，其滚动轴姿态角稳态误差为±1°（由四元数误差转换得到，下同），俯仰轴和偏航轴姿态角稳态误差为±0.5°。图5和图6分别给出了卫星在干扰力矩为3ud情况下qbo和ωbo的变化曲线，相应的三轴姿态角稳态误差分别为±2.5°、±1.5°和±1.5°。

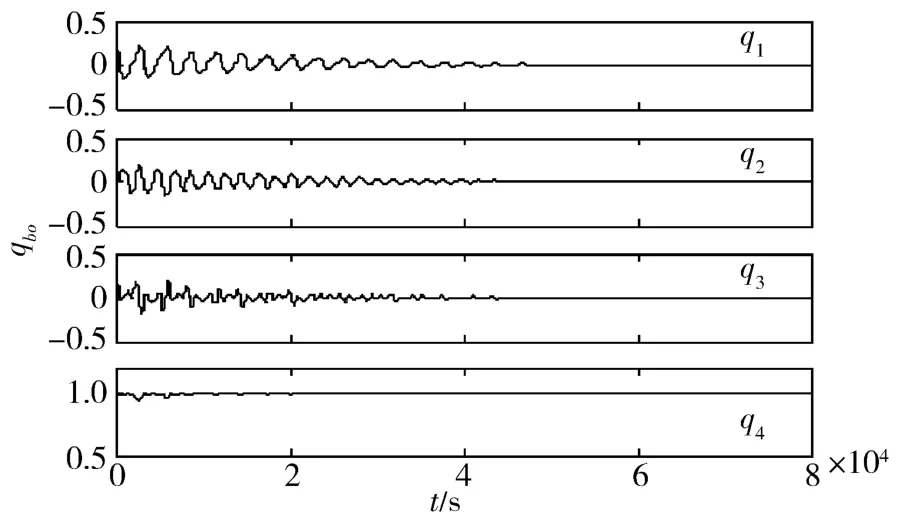
图3 干扰力矩为u d时姿态四元数变化曲线

仿真结果表明，考虑卫星实际运行中受到的干扰力矩，应用本文设计的LQR状态反馈控制律，能够使卫星的姿态四元数和姿态角速度均收敛到平衡点的一个较小范围内。不过由于磁力矩存在方向性约束，在任意时刻只有两轴可控，所以系统一般都需要几个轨道周期才能稳定下来，即调节时间比较长，这也是磁姿态控制不可避免的缺陷。

图4 干扰力矩为u d时姿态角速度变化曲线

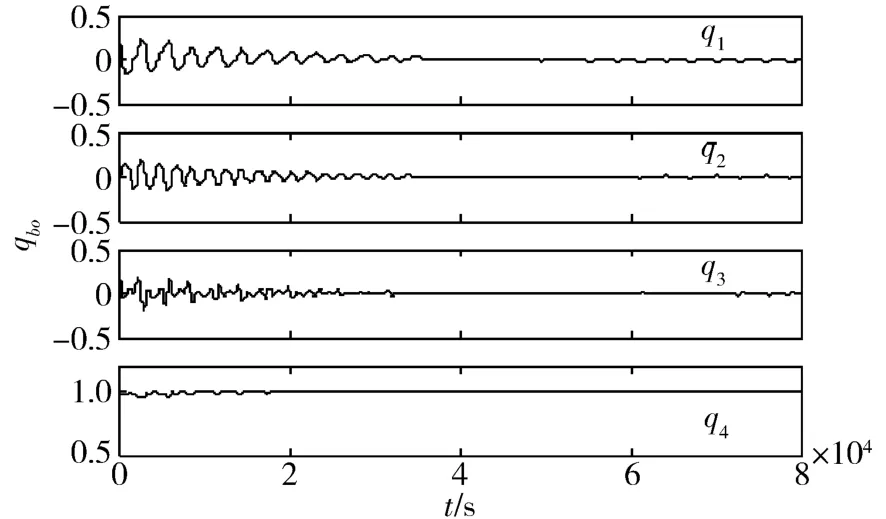
图5 干扰力矩为3u d时姿态四元数变化曲线

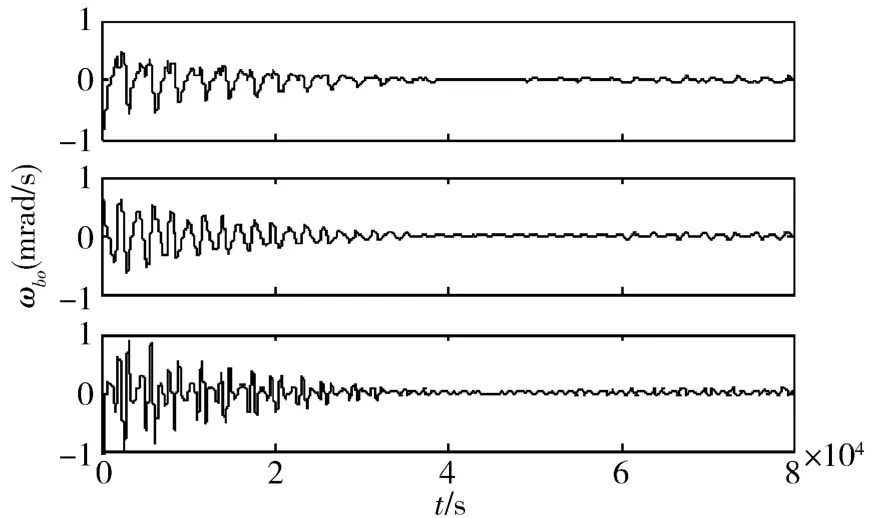
图6 干扰力矩为3u d时姿态角速度变化曲线

5 结 论

本文主要研究了仅用磁力矩器实现小卫星姿态主动控制问题，建立线性化的近地小卫星模型，并基于LQR的无限时间时变最优状态调节器理论设计卫星的线性周期时变系统磁姿态控制律。通过在一个轨道周期内离散地求解代数Riccati方程并将其结果作周期延拓处理，得到周期时变最优磁控制律。数学仿真结果验证了该控制算法在实现三轴姿态稳定任务时的可行性和有效性。

[1] 屠善澄.卫星姿态动力学与控制（1）[M].北京：宇航出版社，1999，49-73

[2] 杨艳.小卫星磁控系统设计仿真研究[D].中国科学院研究生院硕士学位论文，2006

[3] 陈闽，张世杰.飞轮故障时的小卫星轮控与磁控联合控制方法[J].哈尔滨工业大学学报，2007，5（39）：811-816

[4] Silani E，Lovera M.Magnetic spacecraft attitude control：a survey and some new results[J].Control Engineering Practice，2005，13：357-371

[5] Wisniewski R，Markley L.Optimalmagnetic attitude control[C].The 14thIFAC world congress，Beijing，China，1999

[6] PsiakiM.Magnetic torque attitude control via asymptotic periodic linear quadratic regulation[J].Journal of Guidance，Control and Dynamics，2001，24（2）：386-394

[7] Lovera M，Astolfi A.Globalmagnetic attitude control of inertially pointing spacecraft[J].Journal of Guidance，Control and Dynam ics，2005，28（5）：1065-1067

[8] 程国采.四元数法及其应用[M].长沙：国防科技大学出版社，1991

An LQR-Based Magnetic Attitude Control Design for Sm all Satellite

GUO Yanning，LIChuanjiang，MA Guangfu
（Dept.Control Science and Engineering，Harbin Institute of Technology，Harbin 150001，China）

The attitude control problem of low earth orbit（LEO）satellites actuated by magnetorquers only is investigated.By linearizing the nonlinear dynamic and kinematic equations of rigid satellites，a linear periodically time-varing system is obtained.The linear quadratic optimal regulator theory is applied to design an optimal control law for magnetorquers.Simulation results show that the designed optimalmagnetic control law can stabilize three-axis attitude of satellites effectively.

small satellite；attitude control；linear quadratic regulator（LQR）；magnetic control

V448.2

A

1674-1579（2008）05-0061-04

2008-03-31

郭延宁（1985-），男，山东人，硕士研究生，研究方向为航天器姿态确定与控制（e-mail：nning-1@163.com）。