卫星轨迹跟踪控制的参数化方法*

段广仁，谭 峰，张世杰，顾大可

（哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨150001）

卫星轨迹跟踪控制的参数化方法*

段广仁，谭 峰，张世杰，顾大可

（哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨150001）

在卫星轨迹控制系统的状态空间模型的基础上，通过分析卫星的轨道动力学方程，给出卫星轨迹跟踪控制问题的数学描述；基于线性系统的特征结构配置和模型参考理论提出一种卫星轨迹跟踪控制的参数化方法，设计系统的反馈镇定控制器和前馈跟踪控制器。分别进行卫星悬停和绕飞两种指令下的仿真。仿真结果表明，提出的控制方案是行之有效的。

卫星轨迹跟踪；参数化方法；模型参考；悬停；绕飞

1 引 言

近年来，随着航天技术的发展，对卫星的研究越来越受到人们的重视，其中在交会对接、空间拦截撞击、在轨监视或者维修等方面的技术研究迅速发展。一项空间任务的规划，往往从卫星轨迹的跟踪设计和选择开始，分析其稳定性、控制策略和可行性等。在实际工程中，往往需要对卫星的轨道进行调整，即从一个轨道调整到另外一个轨道。轨道调整的过程包括初始轨道的确定、运动过程中轨道的保持以及大幅度的轨道机动。每颗卫星都有其自身的任务，这些任务对卫星运行的轨道都有一定的要求，有些任务需要要求某颗卫星相对于另外一颗卫星、空间站或者大型航天器的相对位置始终保持不变，即跟踪星在目标星轨道下方的某个轨道上运动，并且要求跟踪星和目标星的轨道相位与轨道角速度均相同，但跟踪星的轨道低于目标星的轨道。还有一种情况，要求一颗卫星以另外一个航天器为中心绕飞，这两个航天器同时也绕地球飞行。其中，绕飞卫星围绕另外一个航天器飞行的轨道称为绕飞轨道，也称为伴随轨道[1]。

悬停和绕飞是卫星轨迹跟踪控制中的两个特例。在空间操作技术中，这两种形式的卫星运动具有重要的科学意义和很大的经济价值，可以设计一颗小卫星悬停在目标星下方，或者围绕某个航天器或者空间站飞行，时刻监视目标星的飞行状态、外形结构、工作目的以及随时检查被跟踪的飞行器是否正常工作，从而得到准确的信息并且减少一些不必要的费用。这是卫星的一个新的应用领域。

目前在卫星轨迹跟踪控制方面，国内的研究还比较少。文献[2]给出了卫星的悬停轨道的一种开路轨迹控制策略，并且验证了在一段时间内能够实现对空间目标的悬停。文献[3]和文献[4]对小卫星绕飞轨道的稳定性进行了研究，并给出了存在摄动的情况下绕飞轨道的控制方法。本文基于卫星的飞行动力学，首先建立了卫星轨迹跟踪的轨道动力学模型，并且根据动力学模型得到一般意义下的卫星轨迹跟踪问题的数学描述，将这一问题归结为一个模型参考输出跟踪问题；然后采用基于特征结构配置的参数化设计方法和模型参考理论，给出了控制器设计的一种参数化方法；最后利用计算机数值仿真验证了所设计控制器的快速性和有效性。

2 卫星轨迹跟踪控制的问题描述

2.1 轨道动力学模型

Hill方程是在目标星轨道坐标系内研究跟踪星相对于目标星的运动特性，它是研究卫星轨迹跟踪控制问题的基础。如图1所示，定义目标星轨道坐标系为oxyz，其中坐标原点o为目标星的质心，x轴方向为目标星轨道的切向方向，y轴方向为目标星轨道径向方向，z轴方向垂直于轨道平面，和x轴、y轴构成右手坐标系，c点为跟踪星的质心。

假设目标星沿圆轨道运动，那么可以用下面的Hill方程来描述跟踪星相对于目标星的运动：

式中，x、y和z分别为跟踪星与目标星的相对距离矢量在坐标系oxyz三个方向上的投影为目标星的轨道坐标系oxyz相对于地心惯性坐标系的常值角速度，r为轨道半径，μ为地球引力常数，ux、uy和uz分别为相对应的坐标轴方向上的控制加速度。

图1 目标星轨道坐标系

2.2 问题描述

从Hill方程可以看出，跟踪星相对于目标星的运动在z轴方向上是和x轴、y轴方向上解耦的，而z轴通道上的控制系统作为一个单输入、单输出系统，其设计相对简单，所以在下面控制律设计时只考虑x轴、y轴方向。

下面将Hill方程给出的相对运动方程写成状态空间的描述形式，并给出卫星轨迹跟踪控制问题的描述。

选取系统的状态向量、输出向量和控制向量为

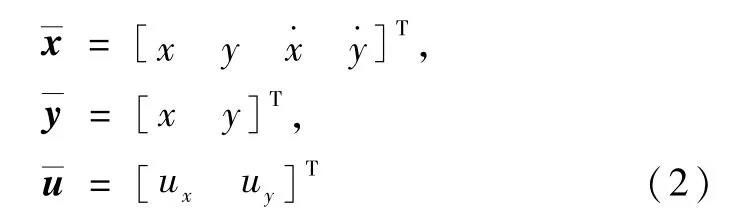
则系统的状态方程为

式中，

问题1.对于系统（3）以及给定的参考信号（t），求取一个控制律，使得闭环系统的输出（t）渐近某一给定的参考信号（t），即

在本文中，如果要使卫星围绕某个航天器或者空间站飞行，那么给定的参考信号可以写成下面的形式：

其中，r、ω0和φ0分别为绕飞半径、绕飞角速度和初始相位角。

另外，若使卫星悬停在另外一颗卫星下面，那么假设已知悬停点的坐标为（xd，yd），则参考信号为

3 控制律设计

由前面的分析可知，对卫星轨迹跟踪控制系统的基本要求是闭环系统稳定并可实现对给定指令的跟踪，这可以归结为一个模型参考输出跟踪问题。考虑一般的情形，设给定的指令信号由下面的参考模型生成

参考模型（7）的含义可能是多方面的。它既可表征所要设计的控制系统的期望响应特性，又可代表被跟踪对象的模型。

要使闭环系统满足条件（4），所设计的控制律应该是受控模型和参考模型的状态组合，即

对此，有以下引理：

引理1[5-6].设矩阵对（A，B）可稳，且存在矩阵Z∈Rn×p和U∈Rr×p满足

则对于系统（3）的任何一个状态反馈镇定律的增益阵K和如下定义的控制律

控制律（8）可以使系统（3）的输出满足式（4）。

根据上述引理，可称控制律（8）中的K阵为反馈镇定器，Kr为前馈补偿器。从而，问题1的求解也可以分为两部分，即反馈镇定器和前馈补偿器的设计。

3.1 反馈镇定器

引入一种基于线性系统特征结构配置的参数化方法来设计系统（3）的反馈镇定器。对于闭环系统为非退化的情形，有如下引理：

引理2[7-9].设A∈Rn×n，B∈Rn×r，[A B]能控；si（i=1，2，…，n）为一组共轭封闭复数（不必互异），则满足关系

的矩阵K∈Rr×n由下述公式给出

其中

N（s）和D（s）为右互素多项式矩阵，满足

fi∈Cr（i=1，2，…，n）为参数向量，满足约束：

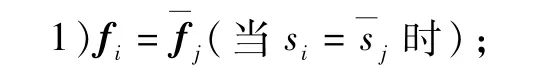
2）det（V）≠0。

对于本文考虑的系统（3），计算得到

引理2给出了状态反馈律的非常简单、整洁的完全参数化公式，其中显含闭环系统的极点，不但可以保证系统的稳定性，而且还可以通过合适地选取极点或在一定区域内优化极点来把握系统的性能；另外，该方法给出了由参向量fi（i=1，2，…，n）表征的控制系统设计中的全部自由度。在实际应用中，可以通过优化这些自由参数来使系统满足希望的各种性能，并使得各种性能得到综合优化。

3.2 前馈补偿器

系统（3）的反馈镇定器确定之后，可以根据引理1的结论进一步计算前馈补偿器。

对于卫星的轨迹跟踪问题，当目标星相对跟踪星的动态特性不明显，或相对运动不剧烈时，例如卫星的悬停和绕飞模式，所跟踪的轨迹可以近似地看作阶跃信号，即有

此时，求解方程组（9），得到U和Z表达式如下：

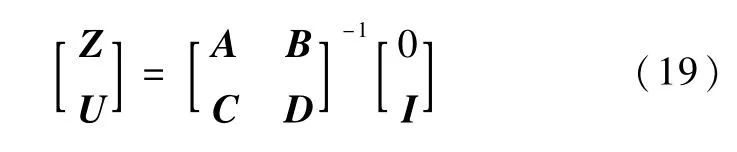
对本文中所考虑的系统（3）而言，上式可以进一步化为

从而有

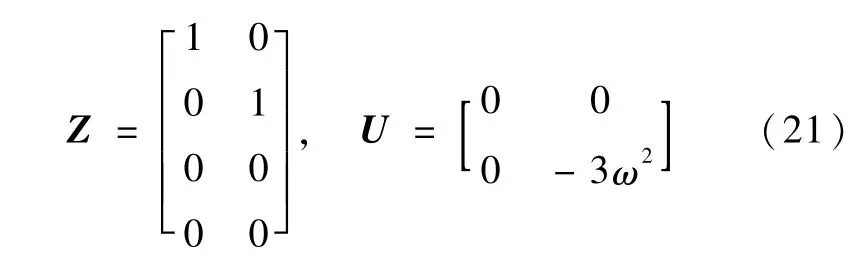
若记

则根据式（10），系统的前馈补偿增益具有表达式

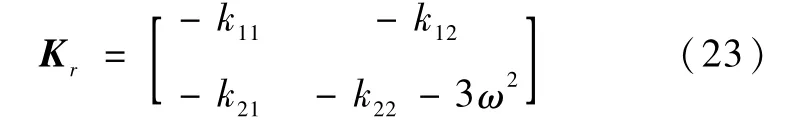
3.3 控制器的优化

由前面的论述可知，当系统（3）给定，其反馈镇定增益K和前馈补偿增益Kr都可以由系统的极点si和自由参量fi唯一确定，si，fi（i=1，2，…，n）给出了控制律（8）的全部设计自由度。我们可以通过在一定区域内优化极点si和自由参量fi使系统满足希望的性能。从而，本文中的控制器求解的问题又可以转化为下述非线性规划问题：

其中，ai、bi、ci、和di给出了系统闭环极点的限制区域，其数值由系统性能要求决定，如快速性和超调等；J为优化指标，可以根据对象的特性和工作要求选定。本文中主要考虑卫星对于给定指令的跟踪性能，因此选取

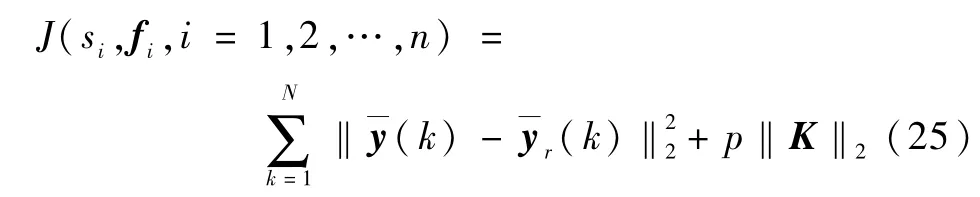
式中，右边第一项为跟踪性能指标，N为所考虑时间段的采样次数，第二项主要是基于节省能量角度考虑，p为加权系数。

利用MATLAB提供的优化工具箱，可以方便地求解上述问题，得到系统闭环极点si和自由参量fi的值如下：

进而根据式（9）和式（10）有：

从而计算得到符合设计指标要求的反馈增益矩阵K和前馈增益阵Kr如下：

注.由上述方法设计得到的控制信号是连续的，假设执行机构可以产生连续的控制力，这对于动量轮系统和配备有脉宽脉频调节器（pulse-width pulsefrequency modulators）的开关式喷气装置都是可实现的。

4 仿真结果及分析

为了验证前面所设计的控制器的有效性，在本节分别进行卫星相对目标星悬停和绕飞两种情况下的仿真。

4.1 绕飞运动模式

假设跟踪星的绕飞轨迹为以目标星为圆心、半径为1000m的圆，如图2中虚线所示。图2和图3分别给出了在本文提出的控制方法下跟踪星围绕目标星飞行的运行轨迹和控制曲线。初始给定的参数如下：

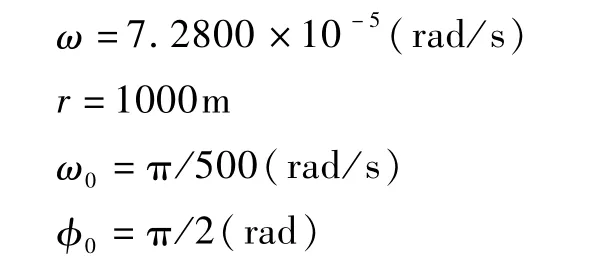
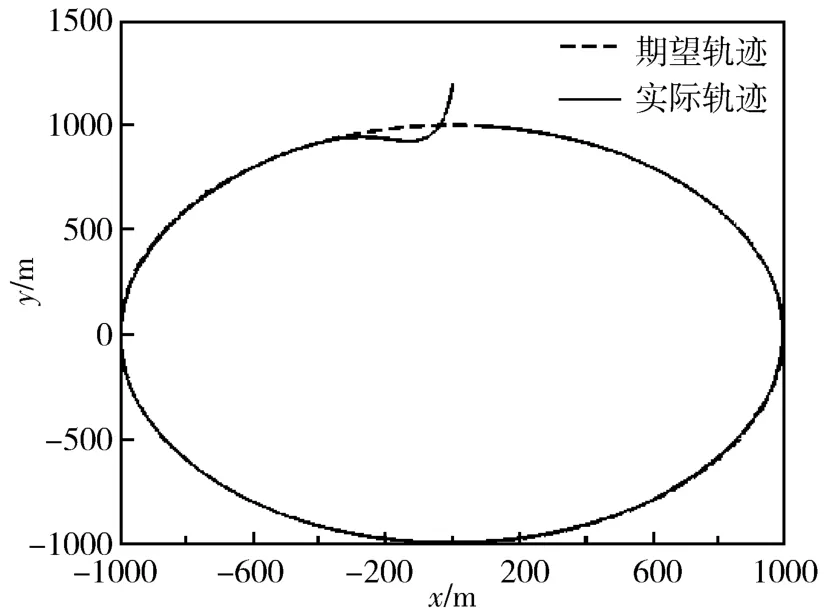
图2 绕飞跟踪星的运动轨迹

图3 实现绕飞径向和切向方向所施加的控制

从上面两个仿真图可以看出，跟踪星在本文设计的控制器作用下，仅以很小的控制力就能够准确、快速地达到期望的运动轨迹，实现对于目标星的绕飞运动。

4.2 悬停运动模式

选取跟踪星的初始状态

悬停位置位于距目标星1000m处，即期望状态

仿真得到的系统输出和控制曲线如图4和图5所示。由仿真图可知所设计的控制系统可以使得卫星快速、准确地到达期望的悬停位置并保持稳定的悬停状态。

图4 悬停跟踪星的运动轨迹

图5 实现悬停径向和切向方向所施加的控制

5 结 论

本文讨论了卫星轨迹跟踪的控制器设计问题，通过分析跟踪星和目标星的相对动力学模型，给出了卫星轨迹跟踪控制问题的数学描述。利用线性系统的特征结构配置理论和模型参考跟踪理论提出了一种控制器设计的参数化方法。文中分别进行了卫星相对目标星悬停和绕飞两种情形下的仿真，结果表明，所设计的控制器能够快速、准确地实现跟踪星对目标星的悬停和绕飞，验证了本文所提控制方案的有效性。

[1] 林来兴.绕飞轨道动力学和控制策略[J].宇航学报，2000，21（4）：100-106

[2] 林来兴，黎康.卫星对空间目标悬停的轨道动力学与控制方法研究[J].中国空间科学技术，2008，（1）：9-12[3] 周文勇，袁建平，罗建军.对异面椭圆轨道目标航天器进行长期绕飞轨迹设计与控制[J].中国空间科学技术，2008，（4）：20-25

[4] 王志刚，陈士橹，袁建平.伴随卫星轨道保持[J].宇航学报，2004，25（4）：398-400

[5] Duan G R，Liu W Q，Liu G P.Robust model reference control for multi variable linear systems：a parametric approach[J].Journal of Systems and Control Engineering，Part I of the Transaction the Institute of Mechanical Engineers，2001，215（6）：599-610

[6] 段广仁，强文义，冯文剑，等.模型参考控制系统设计的一种完全参数化方法[J].宇航学报，1994，15（2）：7-13

[7] 段广仁.线性系统理论[M].哈尔滨：哈尔滨工业大学出版社，2004，188-189

[8] Duan G R.Solutions to matrix equation AV+BW=VF and their application to eigen structure assignment in linear systems[J].IEEE Trans.on Automatic Control，1993，38（2）：276-280

[9] Duan G R.Solution to matrix equation AV+BW=EVF and eigenstructure assignment for descriptor systems[J].Automatica，1992，28（3）：639-643

A Parametric Approach to Satellite Trajectory Tracking Control

DUAN Guangren，TAN Feng，ZHANG Shijie，GU Dake
（Center for Control Theory and Guidance Technology，Harbin Institute of Technology，Harbin 150001，China）

According to the analysis of satellite orbit dynamics，the mathematic description of the trajectory tracking control problem is formulated based on the state space representation of trajectory tracking control systems.A parametric approach is proposed for the satellite trajectory tracking problem by using the eigenstructure assignment theory and the model reference theory of linear systems.A feedback stabilizing controller and a feed-forward tracking controller are built.The designed controllers are applied to the satellite control system and simulation results are given under the hovering over and flying around command signals，which show the effect of the proposed method.

satellite trajectory tracking；parametric approach；model reference；hovering over；flying around

V448.2

A

1674-1579（2008）05-0003-05

*国家自然科学基金（60710002）及长江学者和创新团队发展计划资助项目.

2008-06-11

段广仁（1962-），男，黑龙江人，教授，博士生导师，研究方向为飞行器制导与控制，鲁棒参数化方法等（email：g.r.duan@hit.edu.cn）。