红外地球敏感器测量值修正算法及其应用研究
李明群,魏春岭,袁 军
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
红外地球敏感器测量值修正算法及其应用研究
李明群1,2,魏春岭1,2,袁 军1
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
圆锥扫描式红外地球敏感器常用于测算地心矢量,而地球扁率影响地心矢量精度。研究了基于地球扁率的地心矢量的修正算法,并将该方法应用于双圆锥红外地球敏感器,给出了考虑扁率的地心矢量计算方法。仿真结果表明,该方法能有效地提高地心矢量的计算精度。
地球扁率;地心矢量;圆锥扫描式红外地球敏感器;双圆锥
1 引 言
目前对地定向的三轴稳定卫星大多采用圆锥扫描式红外地球敏感器测量其相对于当地地垂线的姿态,即卫星的滚动角和俯仰角。圆锥扫描式红外地球敏感器利用红外视场扫入和扫出地球边缘时敏感到的地球红外辐射相对于空间背景辐射的变化来确定地平,并由此确定地心方向矢量。红外地球敏感器的测量模型把地球形状假想为标准的球体,但实际的地球形状近似为一个旋转椭球体,因此造成红外地球敏感器的测量误差,称之为红外地球敏感器的扁率误差。这种误差在倾角接近90°的太阳同步轨道中尤为显著。
本文首先对目前基于地球扁率的姿态算法做出综述;接着对一种新型的地球敏感器¯¯¯双圆锥红外地球敏感器如何进行扁率修正作了研究;最后仿真验证了这种双圆锥红外地球敏感器的扁率修正算法,结果表明,进行扁率修正之后,有效地提高了地心方向矢量的计算精度。
2 基于地球扁率的圆锥红外地球敏感器算法
目前研究地球扁率的文献有多篇[1-7],基本都是利用卫星的位置、扫描视场以及扫入扫出点之间的空间几何关系推导扁率误差修正算法,具体方法有两种:1)直接建立椭球条件下的红外地球敏感器测量模型;2)通过测量模型之间的差异修正红外地球敏感器的测量值。两种方法简述如下。
2.1 红外地球敏感器的椭球测量模型
这种算法的思路是:建立基于地球扁率特性的红外地球敏感器测量模型,推导考虑地球扁率的扫描角与姿态角的关系式。以文献[1]为例说明这种算法。为叙述方便,建立如下坐标系:
1)卫星本体坐标系FB:OB-XBYBZB,原点OB位于卫星质心,XB、YB和ZB分别为卫星三个转动惯量的主轴;
2)轨道坐标系FO:OB-XOYOZO,原点位于卫星质心,XO轴与轨道角速度方向一致,ZO轴指向地心,YO轴完成右手正交;
3)敏感器测量坐标系FS:OB-XSYSZS,原点位于卫星质心,YS轴沿红外敏感器的扫描转轴方向,ZS轴垂直于扫描转轴并且使得固连于敏感器的基准点位于OB-YSZS平面内,XS轴完成右手正交。
在上述红外敏感器的安装条件下,根据椭球测量模型,滚动角和俯仰角的表达式为
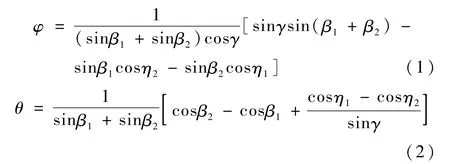
式中β1和β2分别为扫入角和扫出角,γ为扫描半锥角,η1和η2分别为地平穿入矢量和地平穿出矢量与地心矢量的夹角,如图1所示。
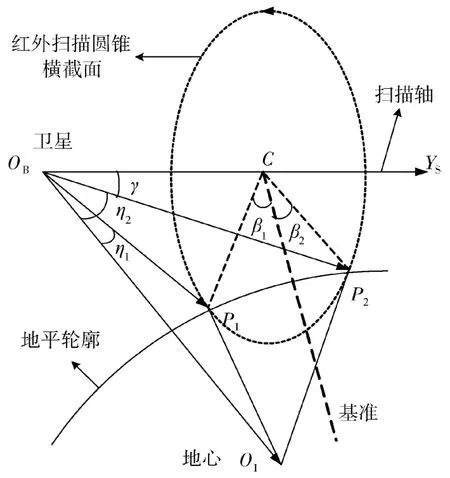
图1 扫描圆锥和地平穿越点
在式(1)和式(2)中,体现地球扁率的量是红外扫描穿入点和穿出点的地球视半径,分别为η1和η2,即
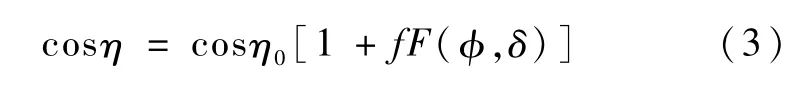
式中,η0是忽略地球扁率时的地球视半径,f是地球扁率,φ是卫星的星下点地心纬度角,δ是地平穿越点的方位角。以地心矢量与地平轮廓椭圆交点为原点,以当地正东为Y*轴、正北为X*轴、Z*成右手正交,建立地理坐标系FG,则地平轮廓椭圆、穿越点P以及方位角δ之间的关系如图2和图3所示。

图2 地平轮廓椭圆和地理坐标系

图3 地平轮廓椭圆和穿越点方位角
此外,式(3)中的函数F(φ,δ)定义为

式中,Re是地球赤道半径,r是卫星到地心距离。
综上可见,若使用式(1)和式(2),需要知道穿越点视半径η的值,因此要先求解穿越点方位角δ,下面简述δ的求解过程。
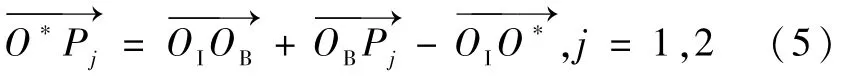

最后对这种基于扁率的红外地球敏感器计算过程做出小结:首先利用式(5)和式(6)计算方位角δ;再将δ代入式(3)和式(4)求出η;最后把η代入式(1)和式(2)即可求出椭球模型下的卫星姿态角。
2.2 红外地球敏感器测量值的扁率误差修正
这种算法利用扁率误差对红外地球敏感器的测量值进行修正。以文献[5]为例,首先计算椭球体和假想球体两种模型下红外地球敏感器扫描角的差值,再以该差值作为补偿量对实际扫描角进行修正,从而得到假想球体模型下的扫描角,参见图4(图中仅示意给出了扫出角的扁率误差,β2和β′2分别是实际扫出角和假想扫出角)。

图4 扫描角的扁率误差
关于扫描角补偿量的计算:首先求解椭球条件下的扫描角。红外视场方向以单位向量表示,地心方向单位矢量以表示,则在地心赤道惯性坐标系下,两者的坐标分别为和那么在地心赤道惯性坐标系中,描述红外视场的射线可由以下参数方程给出
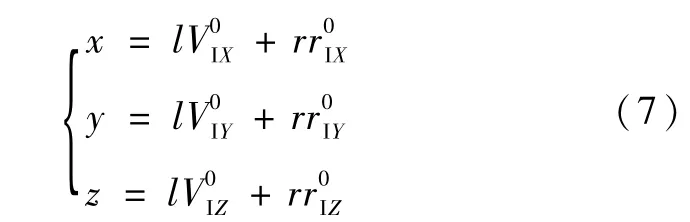
式中,r为地心至卫星的距离,l为参变量。而描述地球椭球表面的方程为
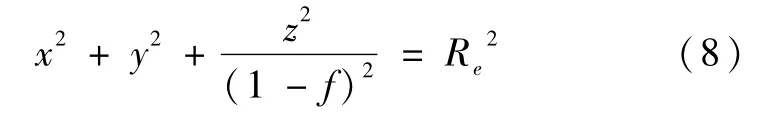
联立式(7)和式(8),得到关于(l/r)的二次方程方程系数


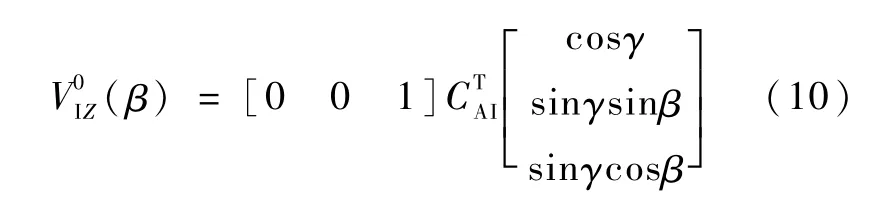
式中CAI是地心赤道惯性系到辅助坐标系的转换矩阵,辅助坐标系由红外扫描轴和星地矢量决定[5]。
如图2所示,红外扫描视场与地球相切于两点(扫入点和扫出点),对应于方程(9)有重根的情形,基于二次方程的根的理论有如下方程:
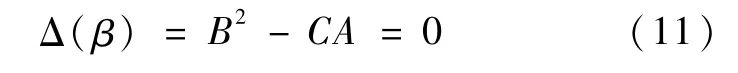
可采用Newton-Raphson法求解方程(11),迭代的初始值可以选取为假想球体模型的扫入、扫出角
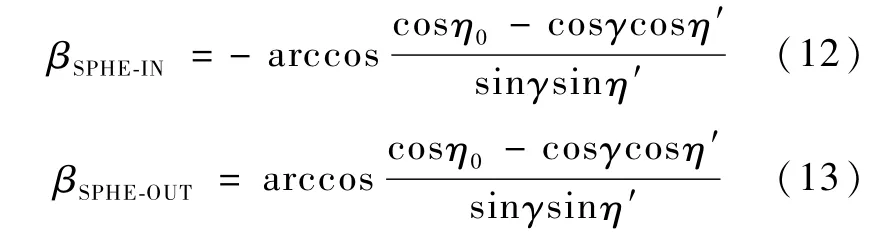
通过迭代可求出任意精度的椭球模型下的扫入角和扫出角,即βOBLA-IN和βOBLA-OUT,与假想球体之间的误差为

综上所述,在红外地球敏感器的实际测量计算过程中,扫描角应做如下修正:

由于地球扁率很小,因此扫描角误差的一阶分量就能满足一定精度要求,所以为了简化计算,修正值可选用用误差值的一阶分量,计算式为
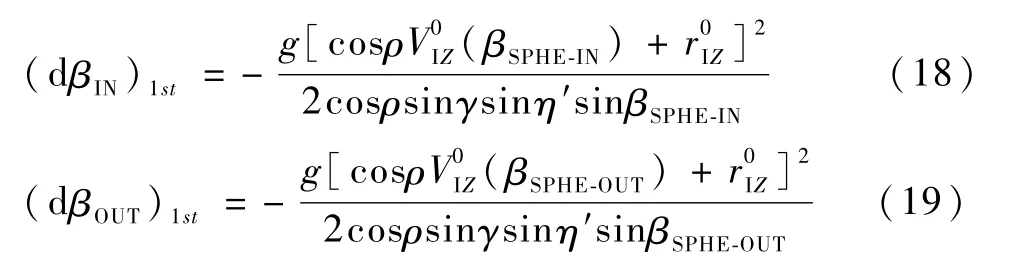
3 扁率修正在双圆锥红外地球敏感器中的应用
双圆锥红外地球敏感器是一种新型地球敏感器[8],用于提取地心方向矢量。如图5所示,双圆锥地球敏感器扫描轴沿卫星本体坐标系XB轴,两个圆锥形红外扫描视场分别记为扫描锥1、2,相应的半锥角为γ1、γ2,Os为地心方向。

图5 双圆锥红外地球敏感器
如果不考虑地球扁率带来的误差,那么在地球的球体模型中,地心方向矢量在卫星本体坐标系的方位角φE(定义为从测量基准YB轴度量到地心方向的圆心角)为
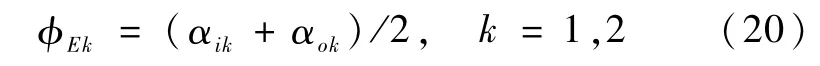
式中αik、αok分别为扫描锥k扫入、扫出地球的扫描角,而红外扫描锥1、2扫描地球的弦宽为
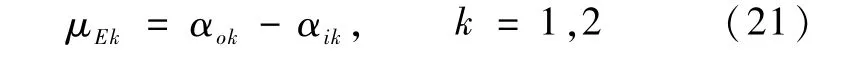
理论上φE1=φE2,将其记为φE。基于球面三角形的关系式[9],有如下方程
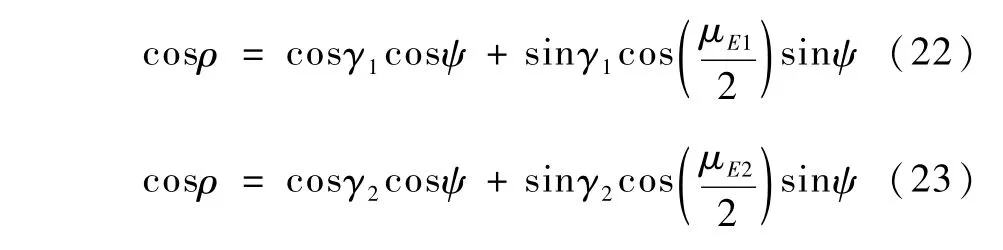
由式(22)和式(23)可以解得天顶距ψ(定义为从XB轴开始度量到地心方向的圆心角)

由式(20)~(24),即可求出地心方向在本体系的方位角和天顶距。则地心方向矢量在本体系的坐标为
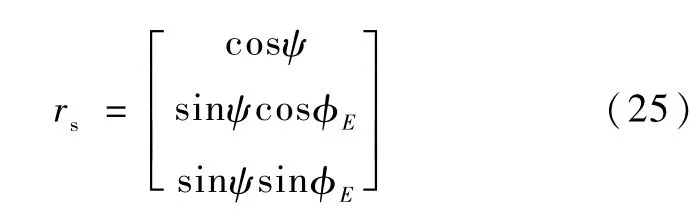
由于地球的扁率,红外扫描锥扫描的不是假想球体,因此式(20)、(22)和(23)不再成立。为了消除这种误差,需要先对测量值作修正,即把对地球实际椭球模型的扫描角修正为对假想球体模型的扫描角。这样可将修正之后的扫描角直接代入原有的计算式。算法物理意义明确,实现简单。具体修正方法如下:

式中,αik-real和αok-real是扫描锥k的实际扫描角,也是对椭球地球的扫描角,αik-sphe和αok-sphe是扫描锥k对假想球体的扫描角,Δαik和Δαok是球体模型和椭球模型扫描角的差值,可利用式(18)和式(19)计算该扫描角的差值。
将通过式(26)和式(27)进行修正后的扫描角代入式(20)~(25),即可得到经扁率修正之后的双圆锥红外地球敏感器的地心方向矢量。
4 双圆锥红外地球敏感器扁率修正的数学仿真
数学仿真中,取轨道为高度h=892km,倾角i=98.7°的圆轨道,地球扁率设为f=0.00392,双圆锥红外地球敏感器的扫描轴安装在XB轴(如图5所示),两个红外扫描圆锥的半锥角分别为γ1=38°和γ2=73°,卫星处于零姿态,方位角φE=90°,天顶距ψ=90°。
首先,不进行扁率修正,把双圆锥红外地球敏感器的扫描角测量值直接代入式(20)~(24),计算地心矢量的方位角φE和天顶距ψ;接着,考虑地球扁率,利用式(18)、(19)、(26)和(27)修正扫描角的扁率误差,再将修正后的扫描角代入式(20)~(24),计算地心矢量的方位角φ′E和天顶距ψ′,图6和图7分别示出经仿真计算获得的扁率修正前和后的地心矢量误差。

图6 未修正扁率时的地心误差
由图6和图7可以看出,未修正扁率时,地心矢量的方位角有0.2°的误差,天顶距有0.05°的误差,扁率修正之后,误差减小了两三个数量级,说明本文提出的修正算法能有效地减小地球扁率给双圆锥红外地球敏感器带来的误差。
另外,从图6中可以看出方位角误差的变化周期等于轨道周期,而天顶距误差的周期等于轨道周期的1/2,并且在两极地区(距离升交点90°、270°左右)的误差较大。对此可以做如下定性的分析:假想的地球模型是一个以赤道半径为半径的球体,与实际地球形状相比,在两极地区的误差最大(如图4所示),因此反映到扫描角上,假想模型与实际模型在两极地区的差别最大,所以计算得到的地心误差在两极地区也最大;另外,根据式(20)和式(24)得出:方位角与扫描角误差之和的周期相同,天顶距与扫描角误差之差的周期相同,根据前述计算模型中标准球体与旋转椭球之差的特点,可知扫描角误差之和的周期等于轨道周期,扫描角误差的周期等于轨道周期的一半,这与仿真结果相符合。
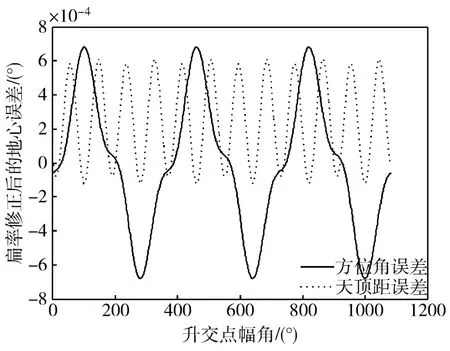
图7 扁率修正后的地心误差
5 结 论
本文研究了基于地球扁率的圆锥扫描式红外地球敏感器的测量算法,按照消除扁率误差的两种途径对目前的算法作了概述,在此基础上研究了扁率误差对双圆锥红外地球敏感器的影响,并提出了相应的修正算法,数学仿真验证了该算法可以有效提高地心矢量的精度。
[1] 周军,钱勇.基于地球扁率红外地平仪测量值修正算法研究[J].宇航学报,2003,24(2):144-149
[2] Hari B H.Roll/pitch determination with scanning horizon sensor:oblateness and altitude correction[J].Journal of Guidance Control and Dynamics,1995,18(6):1355-1364
[3] Jonathan A T,Patrick W,CharlesW G.Scanning horizon sensor attitude correction for earth oblateness[J].Journal of Guidance Control and Dynamics,1996,19(3):706-708
[4] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998
[5] 李捷.基于地球椭球特性的红外地球敏感器测量值的修正算法[J].航天控制,1997,15(4):63-69
[6] Li J.Simple correction algorithms of scanning horizon sensor measurement for earth oblateness[J].Journal of Guidance Control and Dynamics,1999,22(1):187-190
[7] 刘延柱.地球扁率引起红外地平仪姿态测量误差的数学模型[J].宇航学报,1999,20(4):13-17
[8] Collins JT,Conger R E.Mans:autonomous navigation and orbit control for communication satellites[C].The 15thAIAA International Communications Satellite Systems Conference,San Diego,USA,1994
[9] 肖峰.球面天文学与天体力学基础[M].长沙:国防科技大学出版社,1988
Correction Algorithm and Its Application to Measurement of a Scanning Infrared Sensor
LIMingqun1,2,WEIChunling1,2,YUAN Jun1
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.National Laboratory of Space Intelligent Control,Beijing 100190,China)
The scanning infrared sensor is used to measure the geocentric vector.Accuracy of the measurements of the geocentric vector is affected by the earth oblateness.This paper discusses the correction algorithms of measurements of the scanning infrared sensor based on earth oblateness and its app lication in the double-cone scanning infrared earth sensor and then presents a correction algorithm.The simulation shows its validity.
earth oblateness;geocentric vector;scanning infrared earth sensor;double-cone

V448
A
1674-1579(2008)05-0026-05
2008-06-28
李明群(1977-),男,河南人,博士研究生,研究方向为卫星自主导航(e-mail:li-mingqun@163.com)。

