图形变换与图案设计

房玮嘉

平移与旋转是图形的基本变换.利用平移､旋转､轴对称的组合进行图案设计,是中考的重点考查内容之一.

例1 在图1的方格纸中,每个小方格都是边长为1个单位的正方形.△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).

(1)试画出△ABC向下平移4个单位后的图形△A1B1C1;

(2)试画出△ABC绕点O顺时针方向旋转90°后的图形△A2B2C2.

分析:图形的平移作图,应注意平移方向及平移距离;图形的旋转作图,应注意旋转方向､旋转角和旋转中心,同时还有关键点的确定.

解:(1)△ABC向下平移4个单位,则顶点A､B､C分别向下平移4个单位,得到点A1､B1､C1.依次连接点A1､B1､C1,即得平移后的图形△A1B1C1.如图2.

(2)在网格图中作旋转图形,要充分利用网格确定旋转角的大小.连接OA,将线段OA绕O点顺时针方向旋转90°,即可得到点A2.同样地可得到点B2､C2.依次连接点A2､B2､C2,即得旋转后的图形△A2B2C2,如图2.

例2 图3中的四边形是某设计师在方格纸中所设计的某图案的一部分.请你帮他完成余下的工作.

(1)作出该四边形关于直线AB的轴对称图形;

(2)将你画出的部分连同原图形绕点O逆时针方向旋转90°;

(3)发挥你的想象,把得到的图案适当涂上阴影,让图案变得更加美丽.

分析:题(1)属于轴对称方面的作图题,解这类问题的关键是作出已知图形上特征点的对称点.作对称点的主要依据是轴对称的性质:对应点所连的线段被对称轴垂直平分.题(2)是在方格纸上将图形旋转90°,实际上就是找出某些直线的垂线.可先选几个关键点,找出这几个关键点与旋转中心连线的垂线,再由线段相等找出这些关键点的对应点.

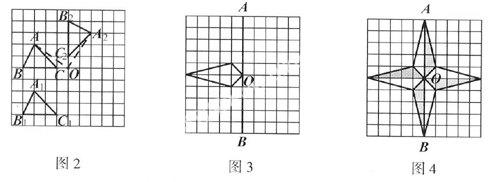
解:如图4所示.

例3 图5中的图形是某设计师所设计图案的一部分.请你运用旋转变换的方法,在方格纸中将图案绕点O顺时针方向依次旋转45°､90°､135°､180°､225°､270°､315°.画出旋转后的图案,并适当涂上阴影,你会得到一个美丽的图案.涂阴影时不要涂错位置,否则就不会出现理想的效果.你来试一试吧!

分析:运用“对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角都相等”等特征,很容易得到答案.

解:运用旋转变换的方法,按照要求进行作图.变换后的图案如图6所示.

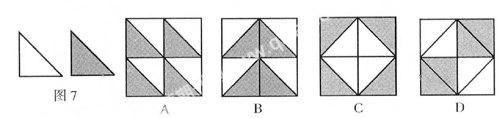
例4 某公司为了节约开支,购买了质量相同的两种颜色的残缺地砖,准备用来装饰地面.现在已经把它们加工成如图7所示的等腰直角三角形地砖.李聪同学设计出A､B､C､D四种图案.

(1)请问:你喜欢其中的哪个图案?描述该图案的形成过程.

(2)请你利用平移､旋转､轴对称等知识再设计一个与上述图案不同的图案.

分析:可选其中一个图案来简述.同一图案形成的过程也不唯一,只要叙述合理即可.例如,图案A的形成过程为:①以两种颜色的地砖组成小正方形作为“基本图案”,再经过平移得到;②以同一列的四块地砖组成的长方形作为“基本图案”,再经过平移得到.

解:(1)我喜欢图案D.其形成过程为:以同行或同列的两个小正方形组成的长方形为“基本图案”,再绕这个长方形某条较长的边的中点旋转180°得到.

(2)如图8所示.

例5 请你设计一个图案,使其绕图形上一点旋转60°后能与自身重合.

分析:因为360°÷60°=6,所以设计时“基本图案”的个数应为6.

解:设计的图案如图9所示.