三角形考点综述
许建霞中学一级教师,现任职于河北任丘市麻家务一中,沧州市学科带头人,曾荣获河北省第二届中学数学青年教师优秀课评比一等奖.
本文将“三角形”一章中的主要考点与题型进行总结,帮助同学们进行期中复习.
1. 三角形的边
考试要求:(1)已知三角形两边的长,会利用三角形的三边关系判断第三边的取值范围;(2)能在复杂图形中正确数出三角形的个数.
例1在△ABC中,AB=3,BC=4,则边AC的长应满足().
A. AC=5 B. AC>1
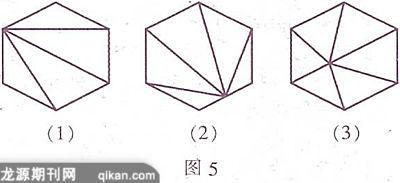
C. AC<7 D. 1 解:由三角形的三边关系可知应选D. 2. 三角形的高、中线及角平分线 考试要求:(1)会画任意三角形的角平分线、中线和高;(2)能在复杂图形中识别这三种线段. 例2如图1,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13 cm,BC=12 cm,AC=5 cm. (1)求△ABC的面积. (2)求CD的长. 解:(1)∵在Rt△ABC中,∠ACB=90°,BC= 12 cm,AC=5 cm, ∴S△ABC=1/2AC·BC =1/2 × 5 × 12=30(cm2). (2)因为CD为AB边上的高,所以S△ABC=1/2AB·CD,即30=1/2× 13 × CD. 解得CD=(cm). [注意:]求直角三角形的面积一般有两种方法: (1)S=1/2ab(a、b为两直角边的长); (2)S=1/2ch(c为直角三角形斜边的长,h为斜边上的高). 由此可知ab=ch,在a、b、c、h四个量中,已知其中三个就可以求出第四个. 例3在△ABC中,D为BC的中点,则△ABD与△ACD的面积的大小关系为(). A.S△ABD>S△ACD B.S△ABD C.S△ABD=S△ACD D.无法确定 解:选C. 3. 三角形的内角与外角 考试要求:会利用三角形的内角和及外角的性质求角的度数. 例4如图2,在△ABC中,D是AC的延长线上一点,∠BCD的大小为_____________. 解:因为∠BCD是△ABC的外角,所以 ∠BCD=∠A+∠B =36°+62° =98°. 4. 多边形及其内角和 考试要求:会利用多边形的内角和公式求多边形的内角和及多边形的边数,会利用正多边形进行镶嵌. 例5一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是(). A. 5 B. 6C. 7 D. 8 解:设这个多边形的边数为n. 由题意,得(n-2)×180°=3×360°-180°. 解得n=7. 故选C. 例6阅读材料:从多边形的边上或多边形内部的一点与多边形各顶点连线,可将多边形分割成若干个小三角形.图3给出了四边形的分割方法,分别将四边形分割成了2个、3个、4个小三角形. 请你按照图3所示的方法将图4中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形的情形. 解:如图5,分别能分割成4个、5个、6个小三角形.出发点位置不同,分割成的三角形的个数也不同.从一个顶点出发、从一条边上的一点(不是顶点)出发、从内部一点出发能将n边形分割成的小三角形的个数分别为:(n-2)、(n-1)、n.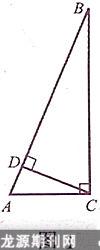



- 中学生数理化·七年级数学人教版的其它文章
- 梦想
- 关于十五子的游戏
- 三元一次方程组的消元策略
- 相交线与平行线知识梳理
- 平面直角坐标系复习导航
- 多边形重点讲练

