平面直角坐标系复习导航

王　锋

王锋中学高级教师，现任职于江苏丰县中学初中部，中国教育学会数学教育研究发展中心优秀会员，中国数学奥林匹克一级教练，数学优秀骨干教师，其业绩被收录于《中国当代 数学家与数学英才大辞典》，参编或主编有多部教学辅导用书，课题“初中数学思想方法”已成功结题.

1. 平面直角坐标系的基本知识

在平面内画两条互相垂直、原点重合的数轴就构成了平面直角坐标系.水平的数轴称为x轴，竖直的数轴称为y轴.两坐标轴的交点称为坐标原点.

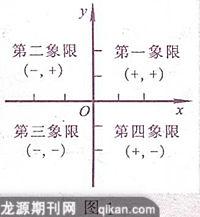
如图1，两条坐标轴将坐标平面分成的四个区域称为象限，按逆时针顺序分别称为第一象限、第二象限、第三象限、第四象限，坐标轴不属于任何象限.

建立平面直角坐标系以后，平面内的点就与一对有序的实数（点的坐标）建立了一一对应的关系.

2. 点与坐标之间的转化

（1）根据点P的坐标（a，b）描出点P的位置：先在x轴上找到表示a的点，过此点作x轴的垂线，再在y轴上找到表示b的点，过此点作y轴的垂线，两条垂线的交点即为要确定的点P的位置.

根据点的位置求点的坐标是上述过程的逆过程.

（2）点的坐标的特征：x轴上点的纵坐标为0；y轴上点的横坐标为0；坐标原点为（0，0）.各个象限内点的坐标的符号如图1所示.

例1在平面直角坐标系中，请将点A（3，3），B（-1，-1），C（1，1），D（5，3），E（-1，-4），F（-5，-2）按下列要求分为两类，并写出同类具有而另一类不具有的一个特征.

（1）点________是同类点，特征是___________.

（2）点________是同类点，特征是___________.

[解析：]点A、C、D是同类点，特征是它们都在第一象限；点B、E、F是同类点，特征是它们都在第三象限.答案不唯一.

3. 平移前后点的坐标之间的关系

一个点向右平移m个单位，其横坐标加上m，向左平移m个单位，其横坐标减去m；向上平移m个单位，其纵坐标加上m，向下平移m个单位，其纵坐标减去m.

例2在平面直角坐标系中，描出点（0，4），（3，1），（2，0），（7，0），（6，1），（9，4），（0，4），用线段将各点顺次连接起来.观察你所描出的图形，你觉得它像什么？将各点的横坐标分别减去3，纵坐标分别减去2，再将它们用线段顺次连接起来，与原图形相比，所得图形有什么变化？

[解析：]如图2，图形像一个碗.各点的横坐标分别减去3，纵坐标分别减去2后，所得各点的坐标依次是（-3，2），（0，-1），（-1，-2），（4，-2），（3，-1），（6，2），（-3，2）.所得图形形状和大小都不变，是原图形先向左平移3个单位长度后，再向下平移2个单位长度得到的.

4. 平面直角坐标系的实际应用

（1）在实际情景中，给出两个物体（可看做点）的位置（坐标），确定另外一个物体的位置时，常采用逆向思维的方法，先根据所给的两个点的坐标，画出平面直角坐标系，然后再由所求物体与已知物体的位置关系找到与它对应的点的坐标.

（2）建立平面直角坐标系，描述物体的位置或求平面图形上某点的坐标时，应根据具体情景或图形特征，选取适当的参照点为原点建立平面直角坐标系.

例3如图3，每个小正方形的边长均为1个单位长度，我们称每个小正方形的顶点为格点，以格点为顶点的三角形叫做格点三角形.

（1）图中的格点三角形ABC是由格点三角形DEF通过怎样的变换得到的？

（2）在图中建立适当的平面直角坐标系，写出△ABC各顶点的坐标.

[解析：]（1）将 △DEF 先向下平移4个单位长度，再向右平移5个单位长度可得到△ABC.

（2）答案不唯一，只要正确建立平面直角坐标系并正确写出各点坐标即可.如按照图4所示的方法建立平面直角坐标系，则点A（0，0），C（2，-1），B（2，3）.