关于十五子的游戏
陈景润
在一张纸上画一个正方形,并把它分成大小相同的十六个方格.再剪出十五个大小相同的正方形纸板,而这些正方形纸板的面积稍小于方格的面积.在这些小纸板上写上1到15这十五个数.这样我们就可以玩十五个子游戏了.把这十五个纸板按任意的顺序放到这十六个小方格中去(如图1).由于每个小方格只能放一个,因而,有一个小方格是空着的.游戏规定:当且仅当纸板与空格相邻时,这个纸板才能和空格相互调换位置,纸板与纸板之间不能调换位置.现在的问题是:能不能经过有限次的移动把这十五个子的顺序排成图2的样子?我们知道,把这十五个纸板按任意顺序放到这十六个小方格中去的方法共有16 × 15 × … × 3 × 2 = 20 922 789 888 000种.若每一种都来试一下,那得花费多少时间呢?于是,我们只能多动脑筋,用心找出这个游戏的规律.
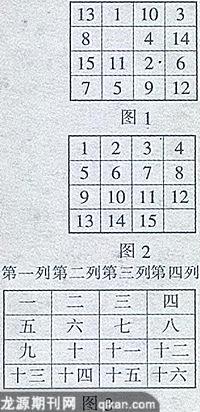
我们不难看出,任一纸板都能经过几次和空格相互对换位置后,移到这十六个小方格中的任一指定的方格中.为了叙述方便,我们将这十六个小方格标上号码,如图3所示.另外我们把十五个纸板分别称为1,2,3,…,15.首先,我们可以把1移到一号位置上,然后,能否把2移到二号位置上呢?这也是可以做到的.若2在第一列,我们可以把它移出第一列,也可以把空格移出第一列,然后第一列不动,而在第二、三、四列中,仿前述方法把2移到二号位置上.1、2的位置确定后,我们不动它,用相同的方法还可以把3移到三号位置上去.这时如果空格不在四号位置上,要想不动1、2、3,而把4移到四号位置上去,却一定不能够做到了.因为在四号位置右边和上边都没有方格,而左边的3又不能动,故只有下边的八号位置与它有联系了.但我们总可以使第一行不动,而把4移到八号位置上,把空格移到十二号位置上,如图4所示.在图4中,我们取出三、四、七、八、十一、十二号位置的六个方格构成图5.为了方便起见,我们将这几号位置中另外三个纸板上的数字分别用甲、乙、丙来代替.然后依次把4往下移,甲往下移,3往右移,乙往上移,如图6.再把甲往左移,4往上移,丙往右移,就变成了图7.在图7中把甲往下移,乙往下移,3往左移,4往上移.此时3、4已分别在三、四号位置上了(如图8).
第一行排好后保持不动,按照安排第一行的方法,当然能够把5、6、7安排在五、六、七号位置上,把8安排在八号位置上.
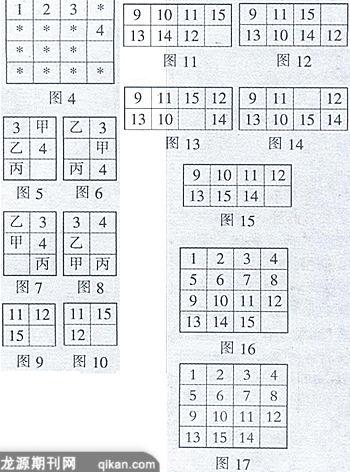
再来安排第三行与第四行时,就要使用不同的办法了.我们不应先排第三行,而应先排第一列下面的两个位置,即九号和十三号位置.这也不难做到,因为我们可以把第一列看成第一行,按照排第一行后面的两个位置的办法来安排第一列后面的两个位置.9和13都已安排好后,按上述办法,我们还能把10、14也安排到十号、十四号位置上,这时只剩下11、12、15这三块纸板还没有安排好.我们可以把11移到十一号位置上,剩下的12、15可能出现下列两种情况:其一是12、15都恰好移到十二及十五号位置上,如图9所示,这正是我们所要达到的目的;也可能出现第二种情况,如图10所示.12排在十五号位置上,而15排在十二号位置上.因为图11可经过图12、13、14变成图15,于是我们知道任给一个初始状态,经过上面的一系列移动后,可以变为图16与图17两种顺序中的一种,我们称图16为正常排列,而称图17为奇异排列.应该说,作为一种游戏,讨论到此就算完了.但如果要问奇异排列能不能重新移动而变为正常排列,哪一种初始状态能变为正常排列,哪一种初始状态要变为奇异排列,那就不得不借助于较多的数学方法了.
(未完待续)
- 中学生数理化·七年级数学人教版的其它文章
- 梦想
- 三元一次方程组的消元策略
- 相交线与平行线知识梳理
- 平面直角坐标系复习导航
- 三角形考点综述
- 多边形重点讲练

