核主成分分析方法在船型方案综合评价中的应用

李冬琴 王丽铮 王呈方

武汉理工大学交通学院 武汉430063

核主成分分析方法在船型方案综合评价中的应用

李冬琴 王丽铮 王呈方

武汉理工大学交通学院 武汉430063

将用于综合评价的核主成分分析（KPCA）方法引入船型方案选优，通过算例分析，将该方法与传统层次分析（AHP）及交互式多目标决策方法进行对比，结果表明该方法在船型方案优选多目标决策问题上是适用和可靠的。

支持向量机回归 KPCA方法 综合评价

最佳船型方案选择是一个多变量、多目标的系统优选排序问题，以前主要靠设计者的经验来判别。随着船舶科学和计算机技术的发展，在船舶设计和船型论证中，通过建立数学模型、采用数学和系统科学方面的优化方法及多准则评价方法等来求解船舶最佳主尺度要素及进行船型论证的研究已陆续出现。

核主成分分析（KPCA）方法是一种操作较简单、在实践中适用性已验证合理的方法。近几年来，该方法得到了大量的应用和提高［1-7］。

引用KPCA方法，对船型方案进行综合分析评价，用于实船的多方案择优排序，取得了较好的效果，从而为多指标决策问题寻找一种行之有效的方法。

1 核主成分分析模型

1．1 简介

核主成分分析（KPCA）是在确保系统原有数据信息量丢失最小的原则下，在各个变量相关关系研究的基础上，将多个变量的信息压缩为几个能反映原问题特征的综合变量指标，并据此特征信息指标对系统进行综合分析，可以有效地来处理变量间的非线性关系，为解决多指标的综合评价提供了一种很好的手段。其基本思想是：通过一个非线性映射Φ，将输入数据xk（k＝1，…，l）（l为输入数据的个数）映射到一个特征空间F，再在特征空间F上进行线性主成分分析。

1．2 模型原理

首先把原空间的数据通过非线性变换Φ投影到特征空间F，假定满足

显然K′的所有特征值λ（λ≥0）和特征向量V满足

定义矩阵K，其中

可以得到

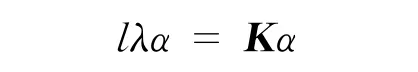
求解该式得到特征值λ1，λ2，…，λl和对应的特征向量α1，α2，…，αl。令

对于主成分的选取，只需计算一个测试点Φ（x）在F上的特征向量νk上的投影

此时KPCA的综合评价函数是

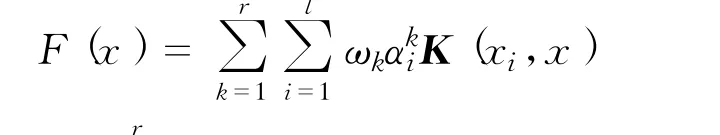
式中：r满足

ωk——对应的第k个主成分的贡献率。若，则K可以用K*表示为

1．3 KPCA方法的具体评价步骤

1）采用标准化处理方法初始化输入样本X，得到矩阵K；

2）求解矩阵K*，

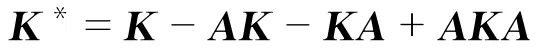
3）求矩阵K*／l的特征值λi（i＝1，2，…，l）和特征向量Vi（i＝1，2，…，l）；

4）找出m个主元对应的特征值λr和特征向量Vr（r＝1，2，…，m）；

5）对每个评价样本求出综合评价函数，进行综合评价。

2 决策矩阵的标准化处理

设多指标决策问题有n个待优选的方案，记为A＝｛A1，A2，…，An｝，评价方案优劣的指标集记为G＝｛G1，G2，…，Gm｝，则矩阵Y＝（yi，j）n×m表示方案集对指标集的决策矩阵

为了消除各“效益型”及“成本型”指标间不可比性，将决策矩阵进行标准化处理。记标准化后的决策矩阵Z＝（zij）n×m，针对不同类型的指标，选取如下公式之一进行处理。对于效益型指标G

对于成本型指标G*

3 应用

引用文献［8］中的数据，以一艘航行于秦皇岛至温州电厂航线的散装运煤船为例，将KPCA方法与文献［8］中的方法相比较，说明该方法的有效性和实用性。抽取G1、G2、G3、G4、G5五项经济指标进行评估，4套待优选方案A1、A2、A3、A4，各方案技术经济指标见表1，具体评价结果见表2。

表1 4种方案技术经济指标对比

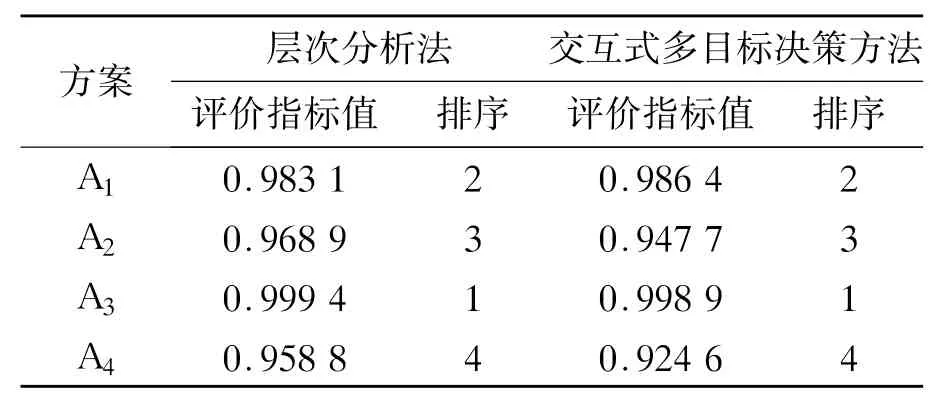
表2 文献［8］中的评价结果

其中文献［8］中，采用层次分析（AHP）方法

得主观偏好权重向量为

采用交互式多目标决策方法得到的综合权重向量为

另外采用KPCA方法，选取多项式核为本试验的核函数，即K（x，y）＝［c（x·y）+m］d；取c＝0．08，m＝0．8，d＝40。通过MATLAB编程计算，得到最大特征值λ＝36．499，最大贡献率为91．908%及相应的评价指标值，结果见表3。比较表2、3，可以看出评价结果完全一样，说明了KPCA方法的有效性和实用性。

表3 KPCA方法综合评价结果

4 对KPCA方法的讨论

传统的AHP方法是通过专家评定各指标的主观重视程度来确定权重，而交互式多目标决策方法是在对指标有偏好信息及客观熵信息输出权重基础上，以最小二乘法为工具，建立确定指标权重的优化模型。不管哪种方法都存在基于对指标的主观偏好信息，免不了带有主观臆断性。

给出的KPCA评价模型可以在没有专家权重的情况下，确定出可信度较高的优选方案，具有较强的客观性和科学性。与传统评价方法相比，KPCA方法有如下特点。

1）核主成分分析方法用于多指标评价，采用的都是信息量权（信息量权属于客观赋权），评价值实际上是二次合成的。其中第一次是以相关矩阵各特征向量分量为权，合成各主成分（其实质是对样本空间实施正交变换）；第二次是以方差贡献率为权，对所选数目主成分求和以合成单值化的综合评价值（其实质是对降维后的主成分空间压缩投影为可排序的一维），合成最终综合评价值。前者是统计分析的本意，后者是评价的要求。

2）KPCA方法不是直接计算特征向量，而是将其转化为求核矩阵的特征向量和特征值，这避免了在特征空间求特征向量，而数据在特征向量上的投影转换为求核函数的线性组合，这大大地简化了计算。

3）KPCA能有效地处理变量间的非线性关系，而且能够提供更多的信息。而评价方案数据之间的关系不是很明确，因而采用KPCA方法作评价较为合理一些。

4）核主成分分析方法的另一个作用就是揭示变量之间的一些关系，而这些关系往往是用别的评价方法或者具体专业知识所难以预料的。

KPCA方法的关键是选择合适的核函数及参数，使得第一主成分的贡献率达到85%以上。对于核函数及其参数的确定尚无很好的方法，主要依靠决策者的经验进行选择，有待今后进一步研究。

［1］殷晓莉，王里克．城市综合竞争力评价研究［J］．生产力研究，2005（11）：92-94．

［2］经 玲，朱甫芹，鲁 绯，孙君社．腐乳感官和理化品质的核主成分分析［J］．中国农业大学学报，2004，9（3）：79-81．

［3］张爱丽，刘清水，刘广利．高校图书馆效率的核评价方法［J］．情报杂志，2003（10）：102-103．

［4］徐义田，王来生，崔文善．核主成分分析（KPCA）在企业经济效益评价中的应用［J］．数学的实践与认识，2006，36（1）：35-38．

［5］朱甫芹．基于KPCA的城镇化水平综合评价［J］．决策参考，2004（1）：40-41．

［6］张爱丽，刘广利，刘清水．科技期刊综合评价模型-KPCA［J］．计算机工程与应用，2003（24）：200-2001．

［7］徐义田．支持向量回归算法的研究及其在食物安全中的应用［D］．北京：中国农业大学，2005：30-70．

［8］桑 松，林 焰，纪卓尚．基于交互式多目标决策的船型技术经济评价决策系统［J］．中国造船，2002，43（3）：1-6．

Application of the kernel principal component analysis method in comprehensive evaluation of ship type

LI Dong-qin WANG Li-zheng WANG Cheng-fang
School of Transportation Wuhan University of Technology Wuhan 430063

The kernel principal component analysis（KPCA）method was applied in the selection of optimal ship type．The method was proved to be effective and practicable for a complicated multivariable multi-objective optimization project，by comparing the numerical resultsin comprehensive evaluation of ship type by KPCA method to those from other common used methods．

ship type KPCA method comprehensive evaluation

U692．6

A

1671-7953（2007）02-0001-03

2006-09-26

修回日期2006-10-31

李冬琴（1979—），女，博士生。