带通型频率选择表面的分析与设计

带通型频率选择表面的分析与设计

李 颖 张立军 王德禹
上海交通大学海洋工程国家重点实验室 上海 200030

采用矢量有限元方法（EB-FEM），利用单个单元和周期性边界条件的独特性质，对无限大频率选择表面进行仿真，借助于有限元软件ANSYS，给出了频率选择表面仿真模型的创建方法，并将计算结果与文献结果进行比较分析，最后对圆环型频率选择表面的设计问题提出圆环单元FSS的新设计模型，并探讨该模型的计算方法。

矢量有限元方法 频率选择表面 优化设计 ANSYS

目前，舰船雷达波隐身设计的一项重点是雷达等观通设备，这些观通设备的特点在于必须发出或接收电磁波，从而会使通常采用的外形和吸波材料技术难于隐身，为此需采取一些特殊手段。频率选择表面FSS（frequency selective surface）是一种很好的选择，是在导电金属上布满周期性缝隙或在介质表面上布满周期性金属贴片的二维周期阵列结构。与电磁波相互作用产生明显的带阻（贴片型单元）或带通（孔径型单元）滤波特性。将其应用于舰船上雷达天线等散射较强的部位（如：雷达罩和隐身桅杆）后，大大地降低了舰船的电磁信号，从而可增强水面舰艇的隐蔽性和生存能力。

对于频率选择表面的分析，迄今已有多种方法，本文采用矢量有限元方法，并借助于有限元软件ANSYS对带通型FSS进行分析与设计。

1 FSS的几何结构及设计参数

图1为无限大、无限薄的二维自由FSS的几何结构。沿两个周期方向的单元间距分别为d1、d2，它们之间的夹角为α，这三者共同表示了FSS的布阵方式。在实际应用中，自由FSS通常是附着在介质层表面或者夹在其中组成的复合结构。介质层厚度和相对介电常数分别用t和ε来表示，见图2。

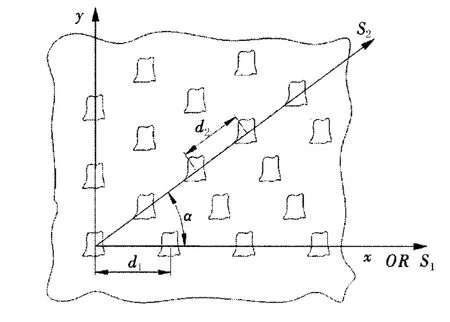
图1 任意开孔的自由FSS

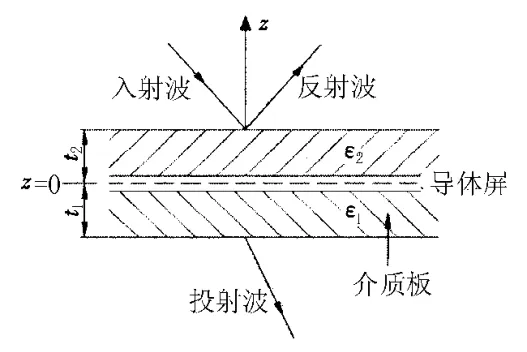
图2 夹在介质间的FSS

不考虑材料损耗，定义电磁波入射方向和+z坐标轴的夹角为θ，并记入射方向在x—y平面上的投影与x轴之间的夹角为φ，（θ，φ）共同表示了电磁波的入射方向，见图3。

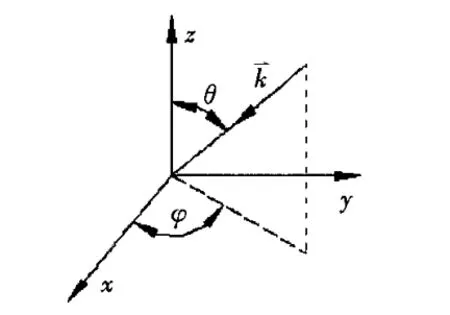
图3 电磁波入射方向

2 不考虑介质衬底时不同布阵方式FSS的仿真与分析

2．1 矩形栅格布阵方式

采用文献［1］中的单元形式为方孔的自由FSS，单元间距d1＝d2＝30 mm，方孔边长15 mm，电磁波垂直入射（0°，0°）。

利用ANSYS能够比较清晰地观察到电磁波的传播情况以及FSS周围的物理变化。图4为当入射电磁波达到FSS的谐振频率8．8 GHz时，所显示的带通特性，此时发生全透射现象。

图4 全投射现象

图5为当入射电磁波达到FSS的节制频率3．0 GHz时，所显示的带阻特性，此时发生全反射现象。并且，从图5中还能够看到驻波，这是由于反射波的存在而导致的。

图5 全反射现象

在已知阵列周期（d1或d2）和电磁波入射角度θ的条件下，利用公式（1）可以预估栅瓣出现的频率f大约为10．0 GHz。

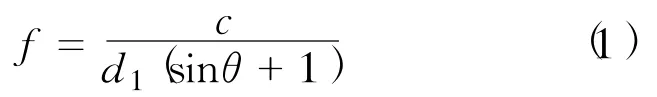
式中：c——光速，c＝3×108ms／2。

栅瓣的出现使得仿真单元在求解计算时也包括了从相邻单元传来的栅瓣场，因此，当入射电磁波的频率高于栅瓣出现的频率时，仿真求解的传输响应结果被认为是没有意义的。从图6中观察到，当频率高于10．0 GHz（图中虚线所示部分）时，传输系数明显偏高，这正是由于相邻单元栅瓣场的贡献所导致的。

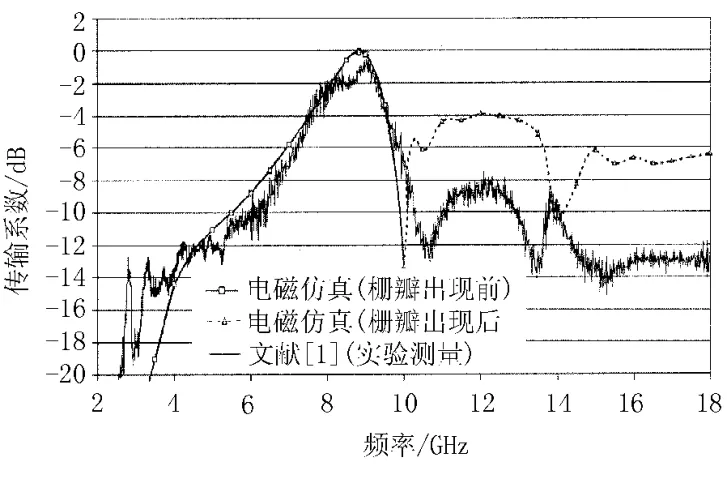
图6 电磁仿真与文献［1］中试验测量的传输响应

通过对比可以看出，在谐振频率点仿真值与文献［1］中的试验测量值大约相差0．5 GHz，其原因可能有：试验中的测量误差；FSS的尺寸不够精准；试验中的FSS是有衬底支撑的；仿真中的网格尺寸划分不够精细。

2．2 三角形栅格布阵方式

采用文献［2］中单元形式为圆孔自由FSS，单元间距d1＝d2＝17．3 mm，圆孔半径r＝6．0 mm，栅格角度α＝60°，电磁波垂直入射（0°，0°）。

模型建立同上。需要注意的是，由于采用三角形布阵方式，使得此时仿真模型的横截面变成夹角为α的平行四边行。仿真结果见图7。

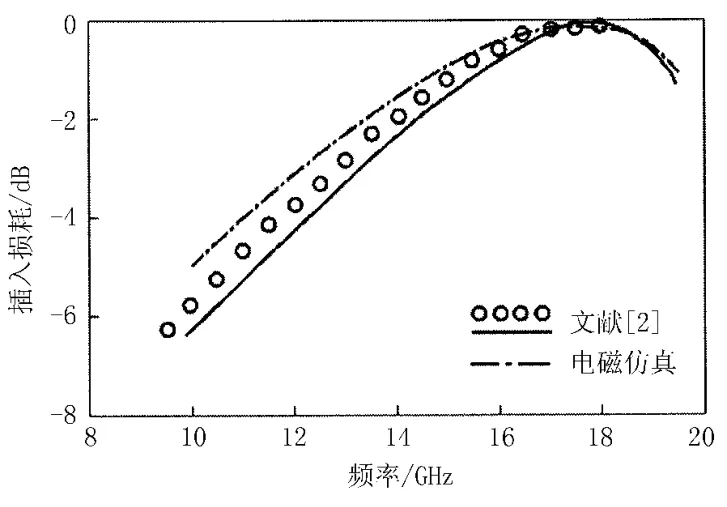
图7 电磁仿真与文献［2］中的插入损耗

此时仿真的谐振频率为17．3 GHz，与文献［2］的试验测量值和计算值相比较，误差均在0．5 GHz以内。由此可见，这种仿真建模方法可行有效。

3 频率选择表面的优化设计

描述带通型FSS性能的两个最重要的指标是中心频率和带宽。其影响参数包括布阵方式、单元形状和尺寸、介质衬底的特性。下面以对称加载介质衬底的带通型圆环频率选择表面［4］的设计为例介绍这些参数的选取。

3．1 已知参数

电磁波极化方式及入射角度的变化范围（θmin，θmax）和（φmax，φmin），中心频率f0，带宽Δf，衬底材料（相对介电常数εr，损耗角正切tanδ）。

将布阵方式、圆环尺寸、衬底厚度所组成的向量记为x∈X＝（d2，α，r1，r2，t）T，TE和TM模波入射时FSS的传输系数分别记为TTE（x，f，θ，φ）和TTM（x，f，θ，φ）。FSS的设计旨在寻求适当的参数x，使FSS在预定的频带中具有良好的滤波特性，此处的设计要使FSS在带内具有良好的传输特性，据此可建立如下的优化模型［3］

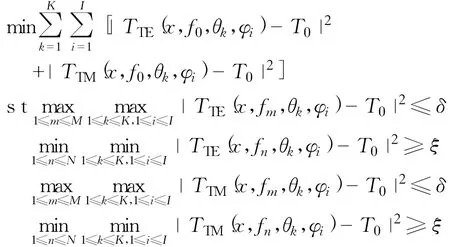
式中：fm——通带内的频率离散值；

fn——通带外的频率离散值。

这里已经将关于f、θ、φ的连续区间离散化。

利用上述方法的两个设计实例，一个不带有衬底，一个带有均匀介质的对称衬底。

3．2 性能要求

1）TE电磁波的入射角

衬底材料的εr＝4，tanδ＝0。

2）中心频率为16．6 GHz；

3）通带内（f0±Δf）的功率传输系数大于95%，即功率衰减δ不大于0．223 dB，其中，Δf＝0．4 GHz；

4）通带外（f0±1．5）的功率衰减ξ不低于10 dB。

3．3 优化设计结果

3．3．1 不带有衬底

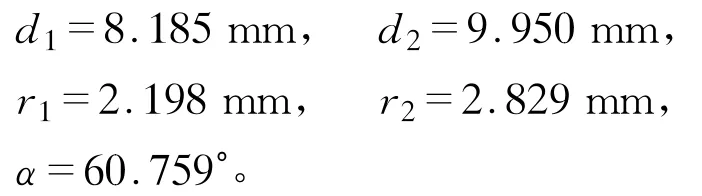
3．3．2 带有均匀介质的对称衬底

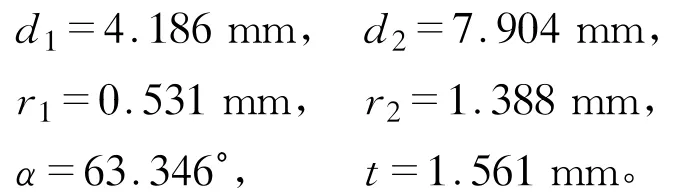
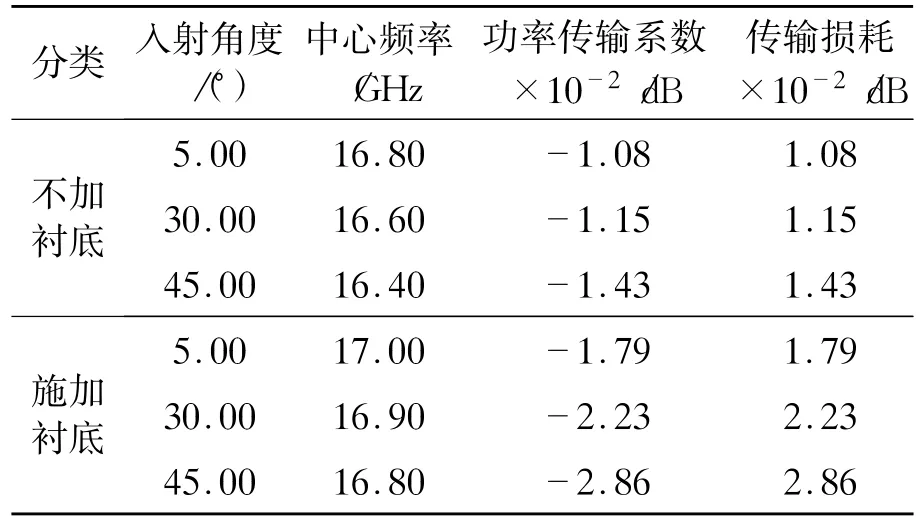
表1 TE入射电磁波（φ＝0°）

从表1中可以看出，对于不同的入射角度，中心频率具有很好的稳定性，并且还具有较高的功率传输系数和较低的传输损耗。因此，此设计结果令人满意。

图8、9给出了该设计在12～25 GHz带宽范围内的功率传输系数曲线。

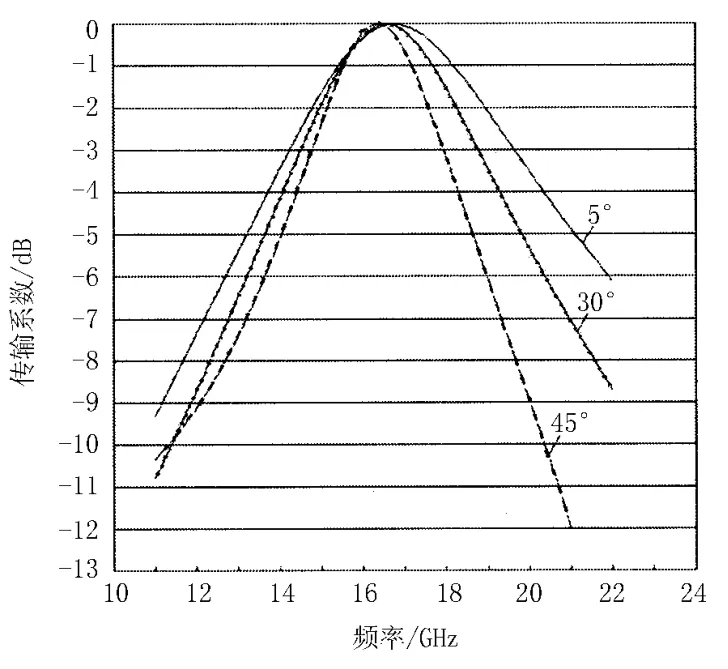
图8 不带有衬底时的功率传输系数

图9 带有衬底时的功率传输系数

4 结论

FSS的设计是电磁学中的一个复杂问题，文中基于矢量有限元理论，利用ANSYS软件研究这类问题，提出了一种针对于该软件的优化设计模型，并给出了其计算方法。新模型及其计算方法具有通用性，适合于各种单元和结构的FSS设计，并且可以用来协调频带内FSS的设计指标。模拟结果表明文中给出的设计方法稳定可靠，且具有良好的可实现性。同时需要指出的是，FSS衬底材料的介电常数和磁导率也可以分别为各向异性的，利用ANSYS也可以对二者的主轴方向进行仿真分析和优化设计，为了减少复杂性，这一点在本论文中没有加以考虑。

［1］Teo P T，Lee K S，Lee C K．Analysis and Design of Band-Pass Frequency-Selective Surfaces Using the FEM CAD Tool［J］．Wiley，2004，14（5）：391-397．

［2］Chen C C．Diffraction of Electromagnetic Waves by a Conducting Screen Perforated Periodically with Circular［J］．IEEE Trans Microwave Theory Tech，1971，19（5）：475-481．

［3］马金平，焦永昌，毛乃宏，陈国瑞．圆环单元频率选择表面的优化设计研究［J］．西安电子科技大学学报，1999，26（6）：767-771．

Analysis and design of band-pass frequency selective surfaces

LI Yin ZHANG LI-jun WANG De-yu
State Key Laboratory of Ocean Engineering Shanghai Jiaotong University Shanghai 200030

Based on the edge-based finite element method（EB-FEM），3-dimensional full-wave analysis and design of band-pass frequency selective surfaces（FSS）is presented．By using the unique features of a unit cell and the periodic boundary conditions，infinite FSSs can besimulated．Thesimulation model was established and analyzed in ANSYS，and the numerical results were compared with the ones in other relational articles．The author also discussed the design of the FSS with ring unit cells，and proposed the novel design model for FSSand its computation method．

edge-based finite element method frequency selective surfaces optimal design ANSYS

TN973．3

A

1671-7953（2007）02-0103-04

2006-09-30

修回日期2006-11-15

李 颖（1978—），女，硕士生。