潜艇耐压液舱区域有限元应力计算

孙 倩 廖建彬 蔡振雄

集美大学轮机工程学院 厦门361021

潜艇耐压液舱区域有限元应力计算

孙 倩 廖建彬 蔡振雄

集美大学轮机工程学院 厦门361021

针对目前潜艇耐压液舱结构应力解析公式精度不高的情况，根据其受力特点建立了同心圆和准同心圆式耐压液舱结构有限元分析的力学模型，编程通过实例计算表明自编有限元程序可靠性很高，可单独作为一个模块取代传统的近似解析法进行应力分析及后续的优化设计。

潜艇 船体结构 有限元 程序

潜艇耐压液舱结构受力复杂，试验表明近似解析法不能反映结构内的真实应力状态。尽管近年来国内外对此展开了广泛的分析研究，先后提出了一些改进的计算方法1-5，但都不够完善。因此在对受力特性最好的同心圆式耐压液舱结构进行了大量的有限元分析的基础上自编了有限元应力计算的源程序，作为一个模块进行最终的优化设计和应力校核。

1 结构型式选择

传统耐压液舱结构（见图1 a））耐压船体应力集中严重、轴向应力很大，同心圆式耐压液舱结构（见图1 b））可以克服这些缺点，但是这种结构型式在布置和通行上会造成不便，以致工程上不太实用。研究表明，如果将同心圆式耐压液舱结构上部的圆弧形液舱壳板改成平板，构成准同心圆式耐压液舱结构（见图1 c）），通过计算，除平台区局部外，基本不改变同心圆式耐压液舱结构的应力分布状态，却可克服上述缺点。相关试验也证明［6］：在弹性阶段，准同心圆式耐压液舱与传统耐压液舱相比，前者船体壳板的应力沿圆周方向趋于均匀化，最大应力明显低于后者相应位置处的同类应力，在外载增长过程中，前者达到局部屈服的时间比后者长，从而验证了准同心圆式耐压液舱结构是一种优良的结构型式。

图1 耐压液舱结构简图

2 力学模型的建立

考虑到以文献［1-5］为代表的近似解析法一般均采用轴对称假设，即将传统的耐压液舱结构简化为一个中间由实肋板相连的双层圆柱壳来分析潜艇耐压液舱的应力分布情况，同心圆和准同心圆式耐压液舱结构更符合轴对称实际，因此也可采用此假设。

2．1 力学模型的选取

以计算精度论，应采用全剖面力学模型，但是它的计算量太大，不利于编程，所以采用中心对称力学模型见图2，即纵向取一档实肋板间距，周向取一个纵骨间距夹角内的结构。此外，通过ANSYS软件计算，验证了平台板的应力如采用解析公式，即应力按四周刚性固定板计算［7］，与有限元结果吻合良好。因此对于同心圆柱壳结构自身的对称性，完全可采用这一力学模型进行计算，而准同心圆式结构的平台板可用解析公式计算，其他部位的应力可采用本文的有限元法的计算结果。

图2 全实肋板加纵骨式耐压液舱结构中心对称力学模型

2．2 有限元网格划分

将耐压液舱和耐压船体壳板周向划分成4个单元，纵向划分成8个单元，其他结构均划分成相当大小的单元。考虑到结构为圆柱形薄壳结构，故采用平面四边形单元，除实肋板采用四边形线性等参元外，其余构件均采用矩形单元。

2．3 边界条件的处理

位移边界条件的选取：两端横剖面上沿圆周的切线和法线方向转角为零，不受外力一端约束纵向位移；在夹角扇面上沿壳板平面切线和法线转角为零；沿夹角剖面的法线位移为零；在耐压液舱纵骨和船体纵骨上三个方向的转角均为零；约束各板单元面内的第六自由度。

在外力方面，假设液舱壳板受法向压力，纵向力则以集中力的形式按力的等效作用原理分配到端面内的各结点上。计算公式参考文献［1］。

3 应力有限元计算源程序编制

根据上述有限元力学模型，用C语言编制有限元应力计算程序。程序流程见图3。

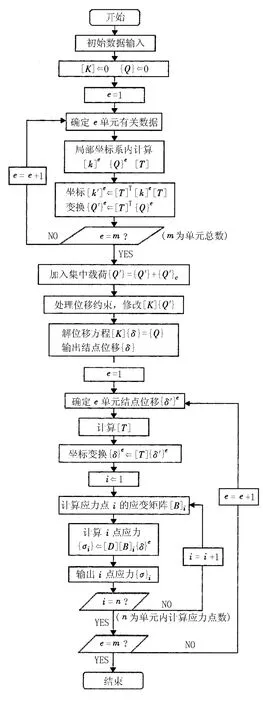
图3 采用平板单元分析耐压液舱结构流程图

3．1 程序编制目的

程序编制的主要目的是为以后的优化设计打基础，因为尽管大型有限元软件如ANSYS、ADINA和NASTRAN等精度功能都比较突出，但明显不适用于在优化过程中的多次频繁调用，而近似解析法的精度又不能令人满意，所以有必要编制一个独立性强并具有较好实用性的有限元程序嵌入到约束函数子程序中取代解析法来计算关键点应力。另外还可以在初步设计阶段可用于校核耐压液舱结构应力。

3．2 程序介绍

该程序由1个主程序、32个子程序组成，可以进行同心圆和准同心圆式耐压液舱结构的有限元应力计算，使用者只需输入计算载荷以及外形尺寸就可以得出各关键点的应力及位移，另外各子程序功能独立，便于移植，使用方便，只要在约束条件子函数中调用该程序就可以进行耐压液舱结构的优化设计。程序流程见图3。

3．3 程序主要特点

程序对整体刚度矩阵采用一维变带宽存储，可放松对结点编号的要求，且适宜用LDLT解法，对受约束的结点方向不建立方程。因此，整体刚度矩阵的阶数为结构的自由度数，自由度序号按结构的结点编号顺序排列。

由于采用了四结点二维等参元，所得到的应力值是单元内高斯积分点处的值，而实际需要的是结点值，因此程序采用了E．Hinton和D．R．J．Owen所提出的局部应力平滑技术［8］，就是一单元的2×2个高斯点的双线性外插应力值，最后按光滑过的应力再求绕结点的平均值，从而得到一个唯一的而且是较满意的结点应力。

对第六自由度采用如下处理：对于局部坐标系的单元刚阵，不管周围单元是否共面，可在其对应于θzi的刚阵对角元素上都加上一个非常小的值ε［9］。这样，当i结点周围单元都共面时，对应于θzi的对角元素也不为零，消除了奇异性；而当i结点周围单元不共面时，由于ε值非常小，也不会影响正常刚度元素迭加结果。这虽然是一种简化的近似处理方法，但实际应用是很方便有效的。

4 实例验证及计算

为验证程序的可靠性，进行若干实例计算。

算例1：全实肋板双层加纵骨同心圆柱壳式耐压液舱结构有限元分析。程序计算结果和采用ANSYS软件的计算结果见表1，两种方法均采用中心对称力学模型。

算例2：全实肋板不加纵骨同心圆柱壳式耐压液舱结构有限元分析。

原始数据同算例1，只是船体及液舱壳板均不加纵骨，ANSYS采用三挡肋位全剖面有限元力学模型，近似解析法采用文献［1］中的方法，计算结果见表2。

算例3：全实肋板液舱壳板加纵骨同心圆柱壳式耐压液舱结构有限元分析。

原始数据同算例1，只有液舱壳板加纵骨，ANSYS采用三挡肋位全剖面有限元模型，计算结果见表3。

算例4：全实肋板液舱壳板加纵骨准同心圆柱壳式耐压液舱结构有限元分析。

此算例计算结果与ANSYS计算结果见表4，ANSYS采用三挡肋位全剖面有限元模型。

表1 全实肋板双层加纵骨典型点结构应力MPa

表2 液舱壳板均不加纵骨典型点结构应力MPa

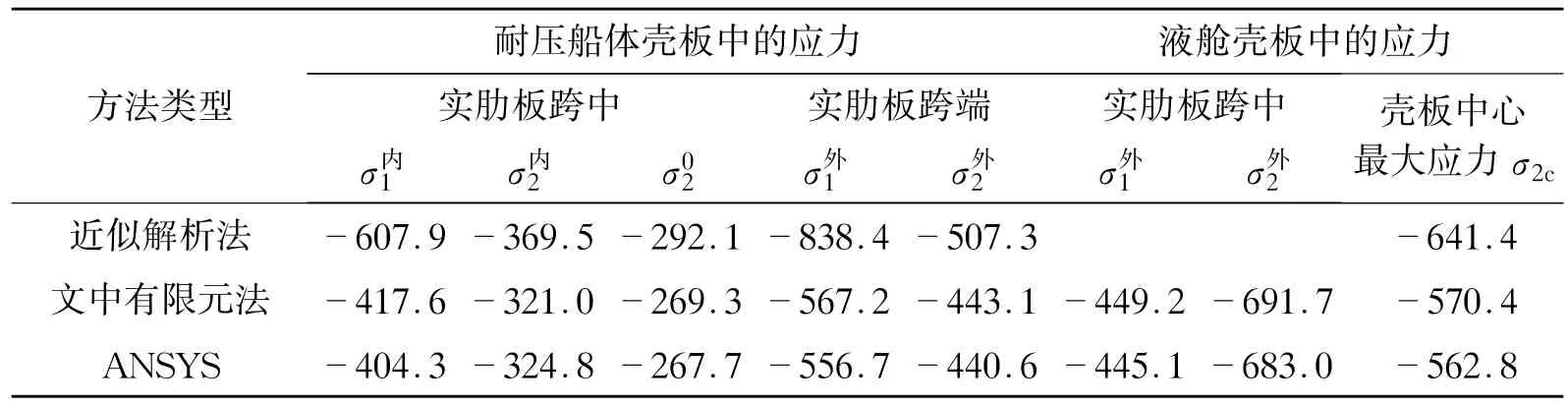
表3 液舱壳板加纵骨典型点结构应力MPa

表4 全实肋板液舱壳板加纵骨典型点结构应力MPa

5 结论

对照表1～4可以看出：

1）仅在耐压液舱壳板加纵骨对耐压船体的应力影响较小，但可以降低耐压液舱的应力；对于双层加纵骨的情况，耐压船体和耐压液舱壳板的轴向应力都有非常明显的下降，耐压液舱的周向应力也有所下降，但耐压船体的周向应力则有所升高。由此说明，壳板加纵骨可显著降低壳板的轴向应力，但有可能造成周向应力恶化。因此，对于同心圆柱壳耐压液舱结构，在耐压液舱上加纵骨是比较好的措施，但在耐压船体上加纵骨就得慎重：如果耐压船体壳板上轴向应力不高，则不必在耐压船体壳板上加纵骨，以免造成周向应力恶化。

2）近似解析法计算出来的耐压船体壳板轴向应力明显偏高而周向应力与有限元结果还比较吻合，文中有限元程序的计算结果与ANSYS的结果比较吻合，两者均采用中心对称力学模型时结果非常接近。误差主要是由于文中基于计算量考虑选用了中心对称力学模型，而ANSYS软件计算考虑到实际情况和世界影响采用的多为较密网格多跨距全剖面模型，另外线性方程的求解、等参元的选择以及第六自由度处理方法等方面都会造成一定的偏差。

综上所述，采用文中编制的有限元程序进行耐压液舱结构的强度分析，误差小于4%，在初步设计阶段可用于校核耐压液舱结构应力，还可以作为单独一个模块取代解析公式进行优化设计。

［1］GJB／Z21-2001．潜艇结构设计计算方法［S］．国防科学技术工业委员会批准发布，2002：8-27．

［2］沈 丰．潜艇纵骨式全实肋板耐压液舱结构强度计算方法（Ⅰ）［J］．舰船性能研究，1994（1）：33-38．

［3］沈 丰．潜艇纵骨式全实肋板耐压液舱结构强度计算方法（Ⅱ）［J］．舰船性能研究，1994（3）：42-46．

［4］罗 斌，陈 强，马 骋．纵骨式全实肋板耐压液舱的纵骨计算方法探讨［J］．舰船科学技术，2004（2）：19-20．

［5］罗 斌，陈 强，徐云椿．潜艇纵骨式全实肋板耐压液舱壳板强度计算方法研究［J］．中国造船，1999（2）：74-80．

［6］谢祚水，孙 倩．耐压液舱结构的模型试验研究［J］．华东船舶工业学院学报，2000（5）：1-4．

［7］陈铁云，陈伯真．船舶结构力学［M］．上海：上海交通大学出版社，1991（7）：197-210．

［8］杨菊生，揽生瑞．有限元法程序设计［M］．西安：西安交通大学出版社，1990（6）：21-103．

［9］赵经文，王宏钰．结构有限元分析［M］．哈尔滨：哈尔滨工业大学出版社，1998（4）：23-39．

FE stress analysis of the pressure tank structure of submarine

SUN Qian LIAO Jian-bin CAI Zhen-xiong
Marine Engineering Institute Jimei University Xiamen 361021

Because of lower accuracy of analytic method，the FE calculation models of the homocentric and quasi-homocentric pressure tank structures were made alternatively according to their properties of loading．The numerical results showed that the programs have high reliability and are suitable for stress analyses optimum calculations in stead of traditional methods．

submarines hull structure finite element method program

U663

A

1671-7953（2007）02-0017-04

2006-08-02

修回日期2006-11-06

孙 倩（1974—），女，硕士，讲师。