肋板形状对肋板式挡墙稳定性影响试验分析
梅明明,罗强,李元昊,张良,蒋良潍
肋板形状对肋板式挡墙稳定性影响试验分析
梅明明1, 2,罗强1, 2,李元昊1, 2,张良1, 2,蒋良潍1, 2
(1. 西南交通大学 土木工程学院,四川 成都 610031;2. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031)
肋板式挡墙是一种依靠肋板与肋板间土体的摩擦效应平衡墙背土压力的新(轻)型支挡结构,其稳定性受肋板形状的影响显著。开展由纸质肋板和有机玻璃面板构成的肋板式挡墙砂箱模型试验,研究3种典型肋板形状对肋板式挡墙稳定性影响规律,分析在极限稳定状态下肋板形状与肋板面积的内在关系。试验结果表明:肋板形状为上小下大的正立三角形肋板面积最小,其次为上大下小的倒三角形肋板,而矩形时所需的肋板面积最大。相对于矩形肋板,正立三角形肋板的面积节约率均值约为25.5%,底部约束的倒三角形肋板约为12.7%,倒三角形肋板约为6.3%;矩形、正立三角形和底部约束的倒三角形肋板式挡墙均为绕墙趾转动的倾覆破坏模式,倒三角形肋板式挡墙则随肋板间距减小由沿墙底滑移破坏模式转变为倾覆破坏;墙体肋板布置间距由疏至密变化,处于极限稳定状态的肋板式挡墙所需肋板长度呈非线性减小趋势,最终趋于稳定。
肋板式挡墙;肋板形状;极限稳定状态;砂箱模型试验;破坏模式

支挡结构在土木工程中有广泛运用。随着工程技术的快速发展,支挡结构的形式已从单纯依靠墙身自重维持稳定的重力式挡墙,发展为采用支撑、土筋复合结构以及锚固技术等多种新(轻)型支挡结构形式,如现有的悬臂式、扶壁式、加筋土式、锚定板式等新型挡墙以及桩板墙、抗滑桩等新型支挡结构。这类新型支挡结构具有结构轻、强度高、稳定性好、节省材料和便于机械化施工等优点[1]。围绕新型支挡结构形式,许多学者开展了深入探讨。王多银等[2]研究了一种新型护岸结构——预应力锚杆无底扶壁挡土墙结构,该结构由立板、肋板和防滑齿墩及预应力锚杆体系组成,适用于岩石地基,尤其是岸坡地形陡峭、无法进行大面积开挖(或进行大面积开挖不经济)地段的良好新型护岸结构。Matsuoka等[3-5]分析的土工袋挡土墙是一种新型加筋土挡土墙结构,具有常规加筋土挡土墙的优势,同时拥有一定的柔性,在墙后土体压力作用下,墙体能够产生一定的变形,能有效减小墙后土压力。WANG等[6]研究了预应力锚杆复合土钉支护结构,该结构将单一的土钉支护置换或增加一定数量的预应力锚杆,在基坑工程实践中得到了广泛运用,具有工程造价低、控制变形好、便与信息化施工等优点。杨佳桦等[7]针对建筑高陡填方边坡土压力巨大,建筑空间有限时,普通悬臂抗滑桩难以满足要求这一问题提出了桁架式抗滑桩,该结构由主桩、副桩和连系梁组成。肋板式挡墙是一种由墙面板与垂直固定连接在墙面板上的肋板组成的新(轻)型支挡结构,主要依靠肋板与肋板间土体产生的摩擦力来平衡作用在墙面板上的土压力,从而实现墙后土体的稳定。姚阳等[8-9]基于砂箱模型试验分析了柔性面板、刚性面板条件下矩形肋板式挡墙的肋板间距合理布置方式,提出了肋板式挡墙随着肋板布置间距由疏到密分别呈现出摩擦锚固型、整体土墙型2种力学作用模式。肋板式挡墙作为一种新型支挡结构,肋板与土体间的相互作用复杂,稳定条件及影响因素有待深入研究。鉴于此,为探究肋板形状对肋板式挡墙稳定性的影响,开展室内砂箱模型试验,研究在刚性面板条件下矩形、正立三角形和倒三角形肋板式挡墙处于极限稳定状态下,所需肋板面积的大小变化规律,以及破坏模式。通过破裂面观察试验,得到肋板间距对矩形肋板式挡墙的破裂面位置影响规律。研究成果可为肋板式挡墙在实际工程应用中提供一定参考。
1 试验设计
1.1 模型砂箱
小型的砂箱模型试验广泛运用于工程模拟中,操作简单,成本低廉,并且可以观察到结构的变形特征[10]。试验采用的模型砂箱几何尺寸为:内部净空间长750 mm,宽500 mm,高500 mm,面板为可拆卸有机玻璃板,箱体侧板与底板均为10 mm厚有机玻璃板,砂箱开口处有一块可拆卸挡板。为防止模型箱变形对实验结果产生影响,在砂箱四周采用不锈钢方管焊接形成钢架,并在距砂箱前方开口60 mm处焊接有U形不锈钢方管,如图1所示。

图1 模型砂箱结构示意图
挡墙面板采用500 mm×500 mm有机玻璃板,板厚度为10 mm。挡墙肋板采用800 g/m2的全灰纸板,纸板厚度为0.15 mm。肋板与墙面板为刚性黏结方式,采用3M双面胶黏接形成模型挡墙。
1.2 砂箱模型挡墙后填土基本物理力学指标
砂箱模型挡墙后填土为干燥的标准砂。采用量瓶法进行了颗粒密度s试验,采用振动锤击法和量筒法分别测定填土的最大干密度dmax和最小干密度dmin,计算得最大孔隙比max、最小孔隙比min,如表1所列。采用筛析法得级配曲线如图2所示。可知,填土平均粒径50=0.35 mm,不均匀系数u=1.9,曲率系数c=1.2,试验所用标准砂为级配均匀的中砂[11-12]。

表1 相对密度及颗粒密度试验

图2 粒径级配曲线
控制砂箱模型挡墙后填土处于中密状态,相对密度r=0.60,对应的干砂填入干密度为d=1.57 g/cm3。通过直剪试验得到填料的抗剪强度≈0,=32.7°。
2 模型试验原理及方案
2.1 模型试验原理
基于砂箱模型的肋板式挡墙试验基本假设: 1) 墙后的填土是理想的散粒体,黏聚力=0;2) 滑动破坏面为一平面;3) 滑动土楔体视为刚体。依据库伦土压力理论[13],填土处于极限稳定状态时,填土内产生通过墙踵的破裂面,破裂面将土体分为滑动区和稳定区,如图3所示。
肋板式挡墙在“长肋疏布”[8]条件下,破坏模式为摩擦锚固型,肋板式挡墙处于稳定的力学机理是墙背受到侧向土压力作用,通过墙面板与肋板的连接,将侧向土压力传递至肋板并依靠位于稳定区的肋板与稳定区土体的摩擦来平衡作用在面板上的土压力。仅改变肋板形状,使得位于稳定区的肋板面积增大,滑动区面积减小,增大了肋板与肋板间土体的摩擦,可提高肋板式挡墙的整体稳定性,如图3所示的正立三角形肋板。
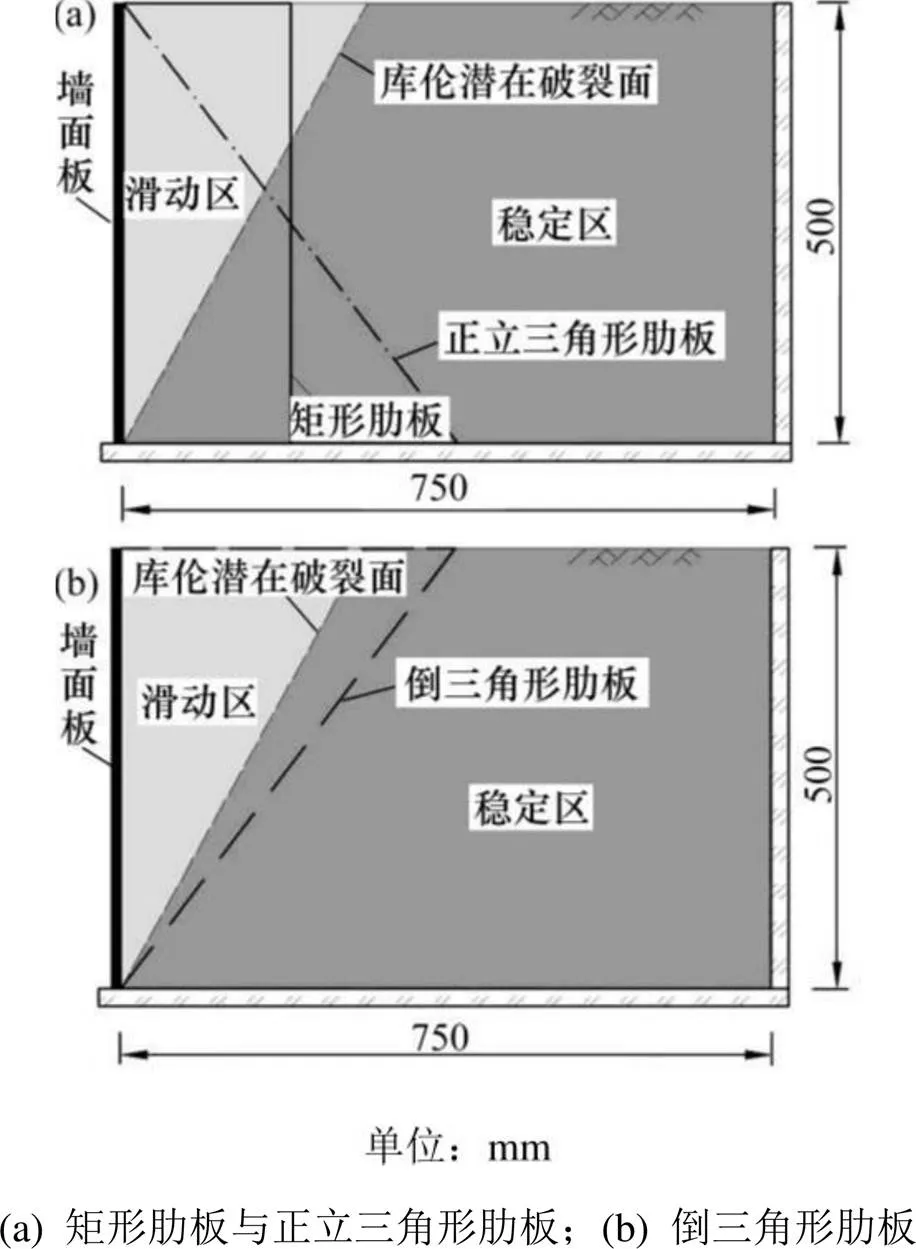
图3 肋板形状与破裂面关系示意
肋板式挡墙在“短肋密布”[8]条件下,破坏模式为整体土墙型,墙面板、肋板、肋间土体形成整体结构。此时,矩形肋板式挡墙受到力的作用形式类似于墙背垂直的重力式挡墙,如图4(a)所示,肋板式挡墙主要受到墙后填土作用于假想墙背的主动土压力a、自身重力、来自地基的支持力+y以及与地基的摩擦力(+y)。
肋板面积保持不变,改变墙背的倾斜角,如图4(b)所示,此时肋板式挡墙类似于墙背俯斜的重力式挡墙。根据库伦主动土压力理论[13],随着墙背由垂直向俯斜转变,墙体所承受的土压力相应增大,图4(b)挡墙的假想墙背受到的土压力a’大于图4(a)挡墙假想墙背的土压力a。由文献[14]可知,在一定范围内增大墙背倾角,可增加挡墙的抗倾覆力矩,增大抗倾覆稳定性。
建立了如图5所示的矩形、正立三角形、倒三角形和底部约束的倒三角形4种肋板式挡墙模型,分别记为模型Ⅰ,模型Ⅱ,模型Ⅲ和模型Ⅳ。其中,模型Ⅰ~模型Ⅲ可在模型箱底板上自由水平移动,可发生滑移和倾覆破坏2种模式;模型Ⅳ墙面板前缘设有水平向位移约束构件,仅可发生倾覆转动 破坏。

图4 短肋密布条件下肋板式挡墙受力简图
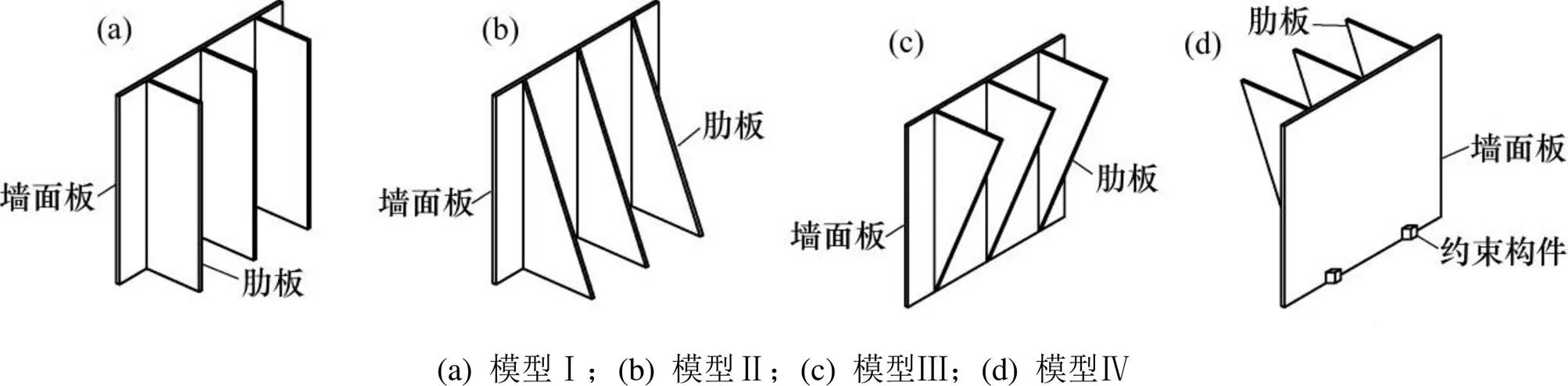
图5 4种挡墙模型示意图
2.2 模型试验方案及步骤
为探究肋板形状对肋板式挡墙稳定性的影响,需得到不同形状肋板的肋板式挡墙在极限稳定状态下的肋板长度。将肋板按设计形状及尺寸进行裁剪并黏接固定在墙面板上,形成肋板式挡墙模型。试验时先将挡板固定,将挡墙模型放入模型箱内,使面板与挡板紧密贴合。分层填筑模型挡墙,每层填筑10 cm,共5层,墙后填土密度按1.57 g/cm3控制。填筑完成后缓慢移去挡板,观察并记录墙体模型是否稳定及破坏形式。试验方案如表2所列。

表2 试验方案
在刚性面板的肋板式挡墙的砂箱模型试验中,肋板布置采用等分面板中线法,如图6所示,为肋板数量,为面板长度。

图6 肋板布置方式示意图
3 试验结果及数据分析
3.1 不同肋板形状模型试验
对3种肋板形状的肋板式挡墙砂箱模型试验,肋板长度按表2所列设计尺寸依次递减,直至填筑模型完成并移除挡板后挡墙失稳。共进行了79组模型试验,其中模型Ⅰ与模型Ⅱ的肋板数量为1~6块,模型Ⅲ与模型Ⅳ的肋板数量为1~8块。
肋板高度与模型墙高相同。定义肋板的长度系数=肋板长度/肋板高度。模型Ⅰ肋板形状为矩形,肋板面积=肋板长度×肋板高度×肋板数量;模型Ⅱ、Ⅲ、Ⅳ肋板形状为三角形,肋板长度为三角形底边长度,肋板面积=肋板长度×肋板高度×肋板数量/2。试验结果如表3~4所列。
取各模型试验在极限稳定状态下所需的肋板长度为极限肋板长度。图7为4种模型的肋板数量与极限肋板长度及长度系数变化曲线。可知,随着肋板数量的增加,4种模型的极限肋板长度逐渐减小最终趋于一个稳定值,模型Ⅰ,Ⅱ,Ⅲ和Ⅳ分别为10,14,16和14 cm,对应长度系数分别为0.2,0.28,0.32和0.28。肋板的长度系数满足模型Ⅲ>模型Ⅳ>模型Ⅱ>模型Ⅰ,即模型Ⅰ肋板的长度系数最小,模型Ⅱ,模型Ⅲ和模型Ⅳ肋板的长度系数分别为模型Ⅰ的1.4~1.6倍,1.7~2.2倍和1.6~2.0倍。

表3 模型Ⅰ试验结果
极限稳定状态下,肋板式挡墙的力学模式为摩擦锚固型时,随着肋板间距的减小,肋板对肋间土体的约束效应逐渐增强,肋板的长度系数随着肋板数量的增加而变小。力学模式为整体土墙时,保持整体土墙的稳定存在一个最小墙厚,所需肋板的长度系数不再随肋板数量的改变而变化。因此,模型Ⅰ与模型Ⅱ的肋板数量在1到4块、模型Ⅲ与模型Ⅳ的肋板数量在1到6块时,对应模型的力学作用模式为“长肋疏布”的摩擦锚固型;当模型Ⅰ与模型Ⅱ的肋板数量到达5块、模型Ⅲ与模型Ⅳ的肋板数量到达7块时,对应模型的力学作用模式为“短肋密布”的整体土墙型。

表4 模型Ⅱ~模型Ⅳ试验结果
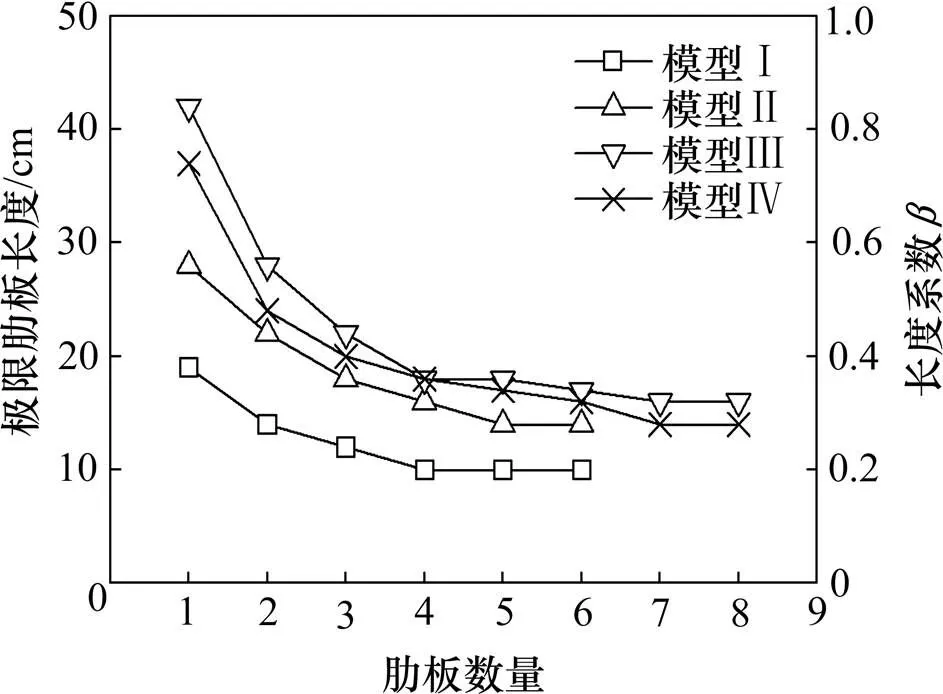
图7 肋板数量与肋板长度及长度系数关系
图8为4种模型在极限稳定状态下肋板数量与肋板面积之间的关系。可得,随着肋板数量的增加,4种模型在极限稳定状态下肋板面积呈近似线性增加。当肋板数量相同时,肋板面积满足:模型Ⅰ>模型Ⅲ>模型Ⅳ>模型Ⅱ。
根据极限肋板长度对应的肋板面积,分别计算模型Ⅱ,模型Ⅲ和模型Ⅳ相对模型Ⅰ的肋板面积节约率。
肋板面积节约率=(模型Ⅱ或Ⅲ或Ⅳ肋板面积-模型Ⅰ肋板面积)/模型Ⅰ肋板面积×100%,如表5所列。计算结果表明,模型Ⅰ所需肋板面积最大,其中模型Ⅱ相对模型Ⅰ的面积节约率在21.4%~ 30%,模型Ⅲ相对模型Ⅰ的面积节约率在-5.3%~ 15%,模型Ⅳ相对模型Ⅰ的肋板面积节约率在0%~ 20%。
4种挡墙模型的破坏模式有倾覆转动、基底滑移2种,如图9所示。模型Ⅰ与模型Ⅱ的抗滑移稳定性大于抗倾覆稳定性,破坏模式均为倾覆转动;由于模型Ⅳ的挡墙底部设有约束构件,其破坏模式为倾覆转动;对于模型Ⅲ,随着肋板间距由大到小逐渐变化,破坏模式由基底滑移过渡为倾覆转动。主要原因为肋板间距较大时,上大下小的三角形肋板挡墙底部约束不强,表现出基底滑移的破坏模式。肋板间距较小时,肋板与肋板间土体形成类似于仰斜墙背的重力式土墙结构,基底抗滑移能力增强,墙体表现出倾覆转动的破坏模式。

图8 肋板数量与肋板面积关系
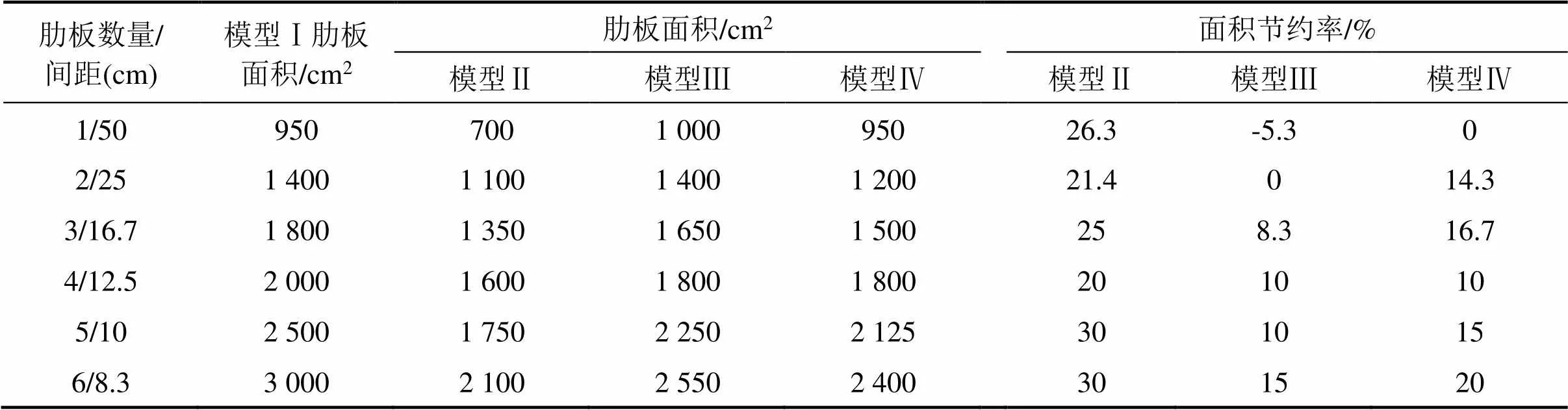
表5 模型Ⅱ~模型Ⅳ肋板面积节约率
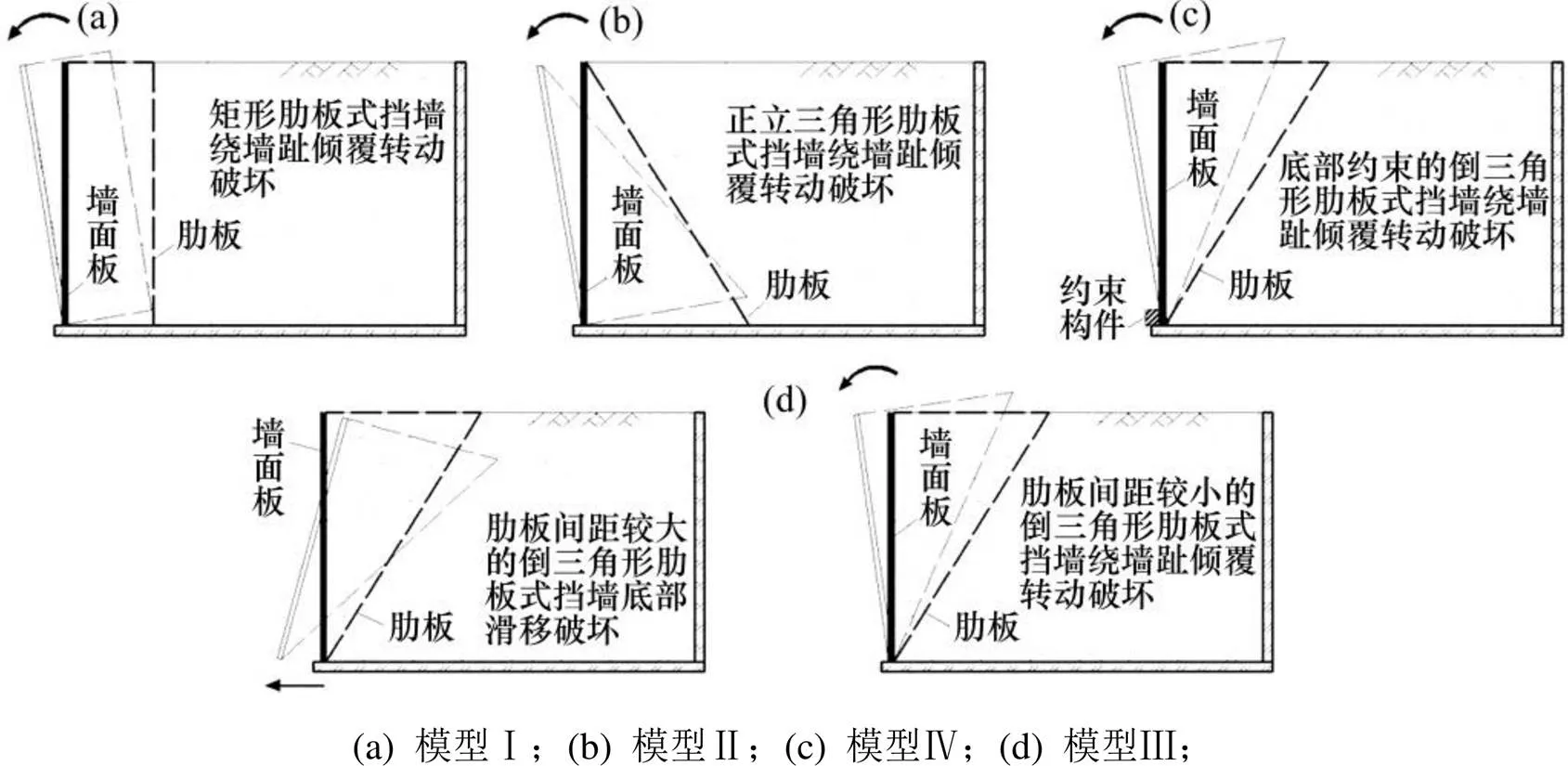
图9 破坏模式简图
3.2 肋板间距对破裂面位置影响
研究对象为矩形肋板式挡墙,不同肋板间距下的肋板长度采用极限肋板长度,试验步骤在分层填筑的基础上,于透明有机玻璃板侧壁每10 cm高度处铺设一层约0.5 cm厚的染色砂,如图10所示。

图10 破裂面位置观察图
缓慢撤离挡板,观察并记录填土表面破裂面位置以及侧面染色砂错动位置。记两侧面染色砂错动处距墙面板位置的平均水平距离为,染色砂错动处距模型箱底板竖直距离,肋板数量为,肋板间距为。试验统计结果见表6。

表6 模型Ⅰ破裂面位置
根据表6的统计数据用直线连接各破裂点,结果如图11所示。在模型试验中,由于模型箱尺寸的限制,模型箱的侧壁存在摩擦约束作用,且土体离侧壁越近该现象越明显[15-16],填土表面的破裂面呈现出曲线的形式,如图10(a)所示,故通过透明有机玻璃板侧壁记录的破裂面倾斜角比实际破裂面倾斜角大。
由图11可知,当肋板间距≤16.7 cm时,破裂面位置有明显往墙后移动的现象,且基本满足随着肋板间距的减小,破裂面位置逐渐远离墙背的趋势。这一现象符合文献[8]提出的肋板式挡墙随肋板间距由疏至密呈现出摩擦锚固型、整体土墙型2种力学作用模式,试验结果进一步验证了该规律。

图11 破裂面分布图
4 结论
1) 极限稳定状态下,正立三角形肋板式挡墙所需肋板面积最小,矩形肋板式挡墙最大,倒三角形肋板式挡墙居中。相对于矩形肋板,正立三角形肋板的面积节约率约21.4%~30%,底部锚固的倒三角形肋板节约率约0%~20%,倒三角形肋板节约率约-5.3%~15%。
2) 矩形肋板式挡墙、正立三角形肋板式挡墙及底部约束的倒三角形肋板式挡墙破坏模式均为绕墙趾转动的倾覆破坏;对于倒三角形肋板式挡墙,随着肋板布置间距逐渐减小,其破坏模式由基底滑移破坏转变为倾覆转动破坏。
3) 随着肋板布置间距由疏至密,极限稳定状态下所需肋板长度逐渐减小最后趋于一个稳定值,最小值约为墙高的0.2~0.32倍,肋板面积呈近似线性增加,相应的肋板式挡墙作用模式由摩擦锚固型转变为整体土墙型。
[1] 李海光. 新型支挡结构设计与工程实例[M]. 北京: 人民交通出版社, 2011. LI Haiguang. Design and engineering practices of new retaining structure[M]. Beijing: China Communications Press, 2011.
[2] 王多银, 兰超, 杨斌, 等. 预应力锚杆无底扶壁结构构造设计[J]. 中国港湾建设, 2005, 25(2): 28-31. WANG Duoyin, LAN Chao, YANG Bin, et al. Approach to structure design of unbased buttressed structure with prestressing anchors[J]. China Harbour Engineering, 2005, 25(2): 28-31.
[3] Matsuoka H, LIU Sihong. New earth reinforcement method by soilbags (“donow”)[J]. Soils and Foundations, 2003, 43(6): 173-188.
[4] LIU Sihong, FAN Kewei, XU Siyuan. Field study of a retaining wall constructed with clay-filled soilbags[J]. Geotextiles and Geomembranes, 2019, 47(1): 87-94.
[5] CHENG Hongyang, Yamamoto H, Thoeni K. Numerical study on stress states and fabric anisotropies in soilbags using the DEM[J]. Computers and Geotechnics, 2016, 76: 170-183.
[6] WANG Hui, CHENG Jianhua, GUO Yuancheng, et al. Failure mechanism of soil nail: prestressed anchor composite retaining structure[J]. Geotechnical and Geological Engineering, 2016, 34(6): 1889-1898.
[7] 杨佳桦, 王凯, 邓丽华, 等. 桁架式抗滑桩与两种抗滑桩结构内力分析对比[J]. 地下空间与工程学报, 2015, 11(增 2): 607-610. YANG Jiahua, WANG Kai, DENG Lihua, et al. Comparison and analysis of internal force of trussed slide resistant pile’s structure with two kinds of anti-slide pile’s[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(Suppl 2): 607-610.
[8] 姚阳, 罗强, 谢涛, 等. 基于砂箱模型试验的肋板式挡墙稳定性及合理布置方式分析[J]. 铁道科学与工程学报, 2016, 13(8): 1499-1506. YAO Yang, LUO Qiang, XIE Tao, et al. The stability and arrangement of ribbed slab retaining wall based on sandbox model test[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1499-1506.
[9] 姚阳. 基于砂箱模型试验的肋板式挡土墙稳定性及破坏模式研究[D]. 成都: 西南交通大学, 2017. YAO Yang. Experiment on stability and failure mode of ribbed slab retaining wall based on sand box model test[D]. Chengdu: Southwest Jiaotong University, 2017.
[10] TONG Hengmao. Sandbox modeling of fault formation and evolution in the Weixinan Sag, Beibuwan Basin, China[J]. Petroleum Science, 2012, 9(2): 121-128.
[11] TB 10102—2004,铁路工程土工试验规程[S]. TB 10102—2004, Code of soil test of railway engineering[S].
[12] TB 10001—1999, 铁路路基设计规范[S]. TB 10001—1999, Code for design on subgrade of railway[S].
[13] 吴曙光. 土力学[M]. 重庆: 重庆大学出版社, 2016: 170-179. WU Shuguang. Soil mechanics[M]. Chongqing: Chongqing University Press, 2016: 170-179.
[14] 任波, 魏新平. 不同形式挡土墙的稳定性分析[J]. 路基工程, 2014(2): 148-152. REN Bo, WEI Xinping. Analysis on stability of retaining wall in different forms[J]. Subgrade Engineering, 2014(2): 148-152.
[15] 徐光明, 章为民. 离心模型中的粒径效应和边界效应研究[J]. 岩土工程学报, 1996, 18(3): 80-86. XU Guangming, ZHANG Weimin. Particle size effect and boundary effect research of centrifugal model[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(3): 80-86.
[16] 姚燕明, 周顺华, 李尧臣. 离心模型试验边界效应分析[J]. 力学季刊, 2004, 25(2): 291-296. YAO Yanming, ZHOU Shunhua, LI Yaochen. Boundary effect analysis of centrifuge test[J]. Chinese Quarterly of Mechanics, 2004, 25(2): 291-296.
Experiment for the influence of rib shape on the stability of ribbed slab retaining wall
MEI Mingming1, 2, LUO Qiang1, 2, LI Yuanhao1, 2, ZHANG Liang1, 2, JIANG Liangwei1, 2
(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)
The ribbed slab retaining wall is a new and light retaining structure, which balances the earth pressure behind the wall by friction effect caused by the ribs and soil mass. The stability of the ribbed slab retaining wall is significantly affected by the shape of the ribs. This paper analyzed the intrinsic relationship between ribs and its area under the limit stable state by a sandbox model of ribbed retaining wall. The result shows that: the smallest area of ribs is the up triangular, and the second is the down triangular, and the rectangular is the largest. Compared with the rectangular rib, the up triangular saves area about 25.5%, the bottom constrained down triangular rib saves about 12.7%, and the down triangular rib saves about 6.3%. Besides, failure mode of the rectangular, the up triangle and the bottom constraint down triangle ribbed retaining wall is overturn around the wall foot, and the down triangular ribbed retaining wall changes from slippage mode along the bottom of the wall to overturning failure with the decrease of rib spacing. With the rib spacing becoming bigger, the length of rib required for the ribbed retaining wall in limit stable state tends to decrease in nonlinear and eventually to be stable.
ribbed slab retaining wall; rib shape; limit stable state; sandbox model experiment; failure mode
10.19713/j.cnki.43-1423/u. T20190289
TU476
A
1672 - 7029(2020)01 - 0039 - 09
2019-04-11
国家自然科学基金资助项目(51878560)
罗强(1963-),男,四川宜宾人,教授,博士,从事高速铁路路基工程研究;E-mail:LQROCK@swjtu.edu.cn
(编辑 涂鹏)

