肋板结构参数对结构刚度的影响研究*

张保成，于喆昌，张开升，杨贵春，王 强

(1.中国海洋大学工程学院机电工程系，山东 青岛 266100；2.中国北方发动机研究所，天津 300400)

加肋板是机械产品常用的一种结构形式，用于加强板结构的刚度特性，以降低结构表面的振动响应及抑制结构的辐射噪声，研究肋板结构参数对板结构刚度特征的影响规律，具有重要意义。

世界各地学者用不同方法对肋板振动特性进行了研究。Bhat[1]利用Rayleigh-Ritz法分析了肋板位置对四边均为简支约束下的正方形板固有频率的影响，他发现当肋板靠近平板边界放置时会显著地增加固有频率。Wiu和Lim[2]分析了约束边界下的中间加肋长方形板自由振动问题，并分析了肋板相对尺寸对弹性约束下加肋板频率的影响。Cheng和Dade[3]采用Gauss样条配置法对加肋板壳进行动态分析。Palani等[4]从2个分离的等参模型分别研究了偏心加肋平板和曲板的静态和自由振动特性。Rao等[5]采用三角形薄壳单元研究加肋板壳结构的固有频率。chen[6]采用曲线分量带法探索了不同加肋平板的自由振动问题，其中包括了四边简支，三边简支一边固定以及三边固定一边简支的情况。Holopanien[7]基于Reissner-Mindlin厚板理论板单元结合刚体梁单元分析了在1或2个方向上放置肋板的固支板的振动。此外，张云鹏[8]利用有限元的方法分析了加肋板横截面积对固有频率的影响。

综上所述，近年来在不同结构参数下的加肋板振动特性进行了大量的研究，但对于肋板的具体结构参数对板结构刚度特征的影响规律尚缺乏研究。本文采用有限元方法，将静、动态刚度作为一个表征参数分析了肋板结构参数对结构刚度的影响规律，已期对广泛采用板式结构形式的机械产品的结构设计提供设计参考。

1 结构模型

为考察肋板结构参数对板结构刚度特征的影响规律，以不同结构参数的肋板为研究对象，以结构的静、动态刚度为评价指标，研究肋板的高度、宽度、数量及位置等设计参数对板结构刚度的影响规律。定义静态刚度作为表征参数，即用单位力作用于非约束边中点时结构的最大变形的倒数为静态刚度。静态刚度对比研究对象是1∶1的光板，三边约束，一边自由，在不同肋板参数下作用单位力，作用点为自由边中点，获得其静态变形，如图1所示。定义相同边界条件下的无肋板结构变形和刚度为基准变形和基准刚度，定义刚度比为加肋板与无肋板基准值的比值。定义结构的前五阶模态频率之和为动态刚度评价指标，以综合分析肋板结构参数对模态频率的改变量。由于在同等边界条件下，结构的静态变形和动态变形仅相差放大系数，因此，静态刚度能够反映结构在动载荷作用下的变形量。

图1 加肋板边界及受载Fig.1 The boundary and loading of stiffened plates

本文肋板结构参数包括高度、宽度、数量及加肋位置对结构刚度的影响规律，如图2所示，肋板宽度与高度尺寸参数分别沿X、Y方向变化；在此基础上，保持其它参数不变，进一步研究肋板数量及肋板位置对加肋板结构刚度的影响规律。

图2 肋板纵横加强方式Fig.2 The mode of strengthening the vertical and horizontal rib

2 肋板高度与宽度的影响研究

增加肋板纵向高度是增加肋板转动惯量的主要措施之一，本节以3 mm×3 mm肋板为最小肋板尺寸，纵向高度或者横向宽度以3、6、9、12、15 mm的尺寸变化共六组数据。利用有限元的方法计算肋板的最大变形量及前六阶频率值，得出加肋板结构静、动态刚度比，对比研究肋板高度与宽度对加肋板结构刚度的影响规律。

2.1 结构刚度计算

加肋板基本尺寸为250 mm×250 mm，厚度为3 mm，采用二次六面体单元进行网格划分，利用有限元软件计算不同高度参数或宽度参数下加肋板的最大变形量及前六阶频率值，不同高度参数下的加肋板前六阶频率值见表1，不同宽度参数下的加肋板前六阶频率值见表2。

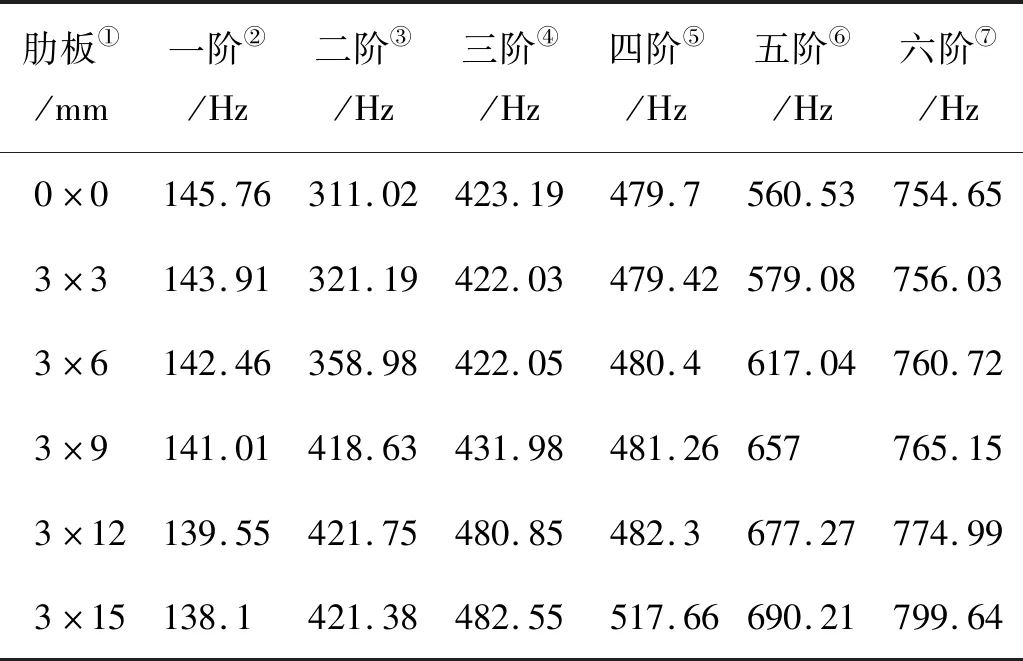
表1 不同肋板高度的加肋板固有频率Table 1 The natural frequency of stiffened plate with different rib height

Note:①Rib;②First order;③Second order;④Third order;⑤Forth order;⑥Fifth order;⑦Sixth order

表2 不同肋板宽度的加肋板固有频率Table 2 The natural frequency of stiffened plate with different rib width

Note:①Rib;②First order;③Second order;④Third order;⑤Forth order;⑥Fifth order;⑦Sixth order

根据文中对静、动态刚度评价指标的定义，以无肋板结构变形和刚度为基准变形和基准刚度，保持其他参数不变，计算不同高度或宽度参数下各加肋板静、动态刚度比，不同肋板高度情况下的加肋板刚度比计算结果见表3，不同肋板宽度情况下的加肋板刚度比计算结果见表4。

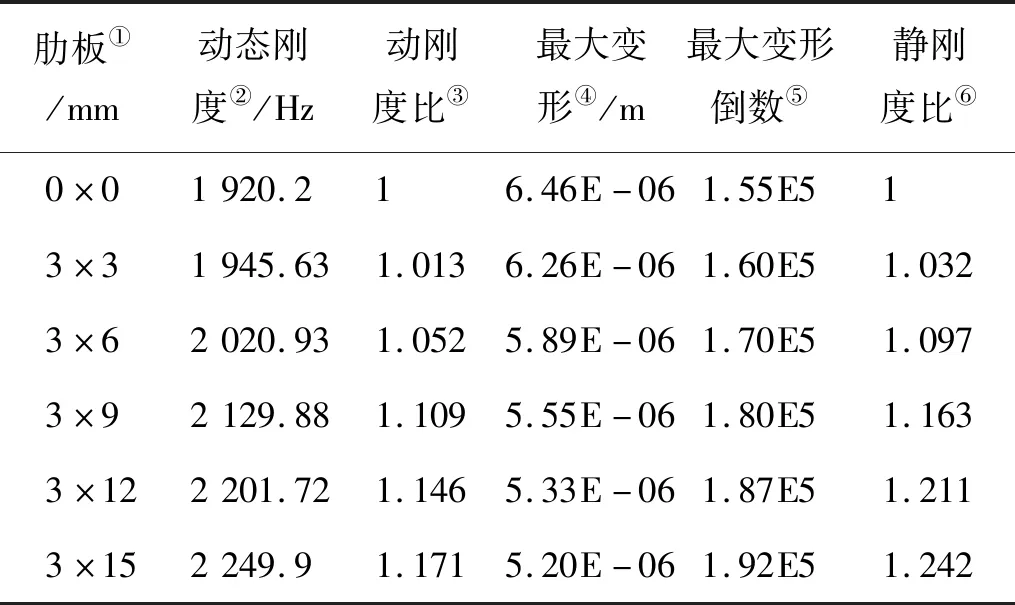
表3 不同肋板高度的加肋板刚度比Table 3 The stiffness ratio of stiffened plate with different height of the ribbed plate

Note:①Rib;②Dynamic stiffness;③Dynamic stiffness ratio;④Maximum deformation;⑤Reciprocal of maximum deformation;⑥Static stiffness ratio

表4 不同肋板宽度的加肋板刚度比Table 4 The stiffness ratio of stiffened plate with different width of the ribbed plate

Note:①Rib;②Dynamic stiffness;③Dynamic stiffness ratio;④Maximum deformation;⑤Reciprocal of maximum deformation;⑥Static stiffness ratio

2.2 对比分析

依据结构动力学相关理论，对表3、4仿真数据进行处理，将肋板高度参数与宽度参数无量纲化为加肋板板厚的倍数，分别绘制静态刚度对比图与动态刚度对比图，见图3、4。

图3 肋板尺寸参数对静刚度的影响Fig.3 Influence of static stiffness of rib size parameters

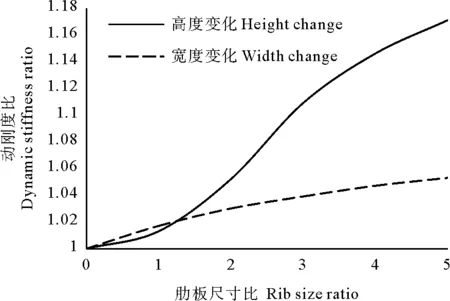
图4 肋板尺寸参数对动刚度的影响Fig.4 Influence of dynamic stiffness of rib size parameters

由图3、4可见，肋板的增加并不能线性增大结构的静、动态刚度，随着肋板宽度或高度增加，静动态刚度趋势均变缓，纵向肋板在板厚2～4倍高度时对加肋板静态刚度的增强效果最大。肋板的高度参数对结构刚度的影响远大于肋板宽度参数对结构刚度的影响。

加肋板的截面示意图见图5，加肋板的截面惯性矩表达式为：

(1)

式中：e1、e2为重心到相应边的距离。

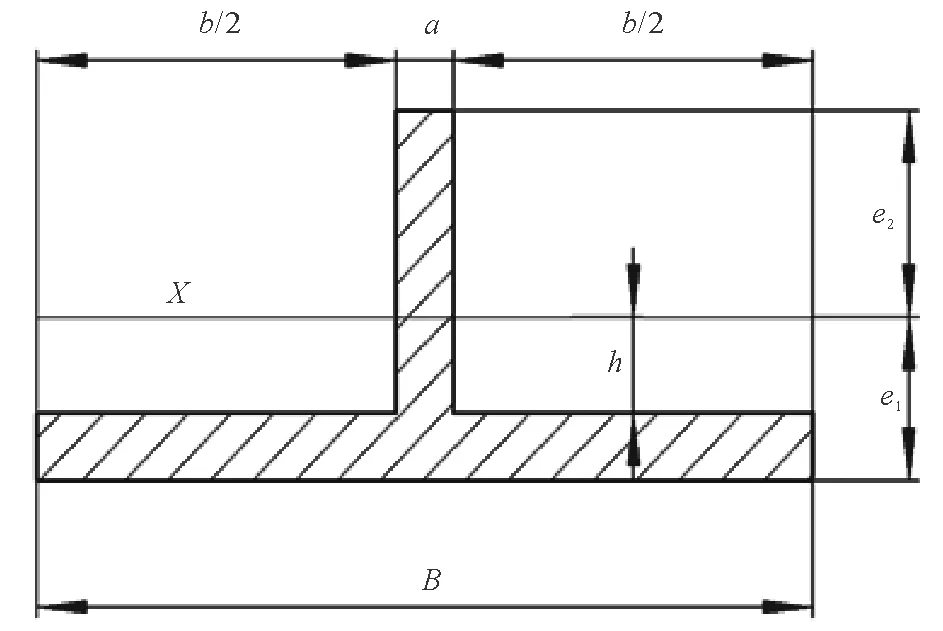
图5 加肋板截面示意图Fig.5 Diagram of stiffened plate cross section

不同高度参数或宽度参数的肋板对加肋板重心位置影响很小，由式(1)可知：在相同肋板宽度下，加肋板截面惯性矩的增量近似与肋板高度的三次方成正比；在相同肋板高度下，加肋板截面惯性矩的增量与肋板宽度成正比。因此，增加肋板高度方向的尺寸更有利于提高加肋板结构刚度。

3 肋板数量与位置的影响研究

本节研究在肋板总体积相同的情况下，肋板数量与位置对加肋板静、动态刚度的影响规律，以无肋板结构变形和刚度为基准变形和基准刚度，以3 mm×12 mm为最大单肋板尺寸，肋板数量按1、2、3、4的变化共4组数据，肋板均布在光板上。

3.1 肋板数量对刚度的影响研究

加肋板基本尺寸为250 mm×250 mm，厚度为3 mm，采用二次六面体单元进行网格划分，利用有限元软件计算各加肋板的前六阶频率值，进一步计算各加肋板最大变形量及静、动态刚度比，各加肋板固有频率值见表5，各加肋板静、动态刚度比见表6。

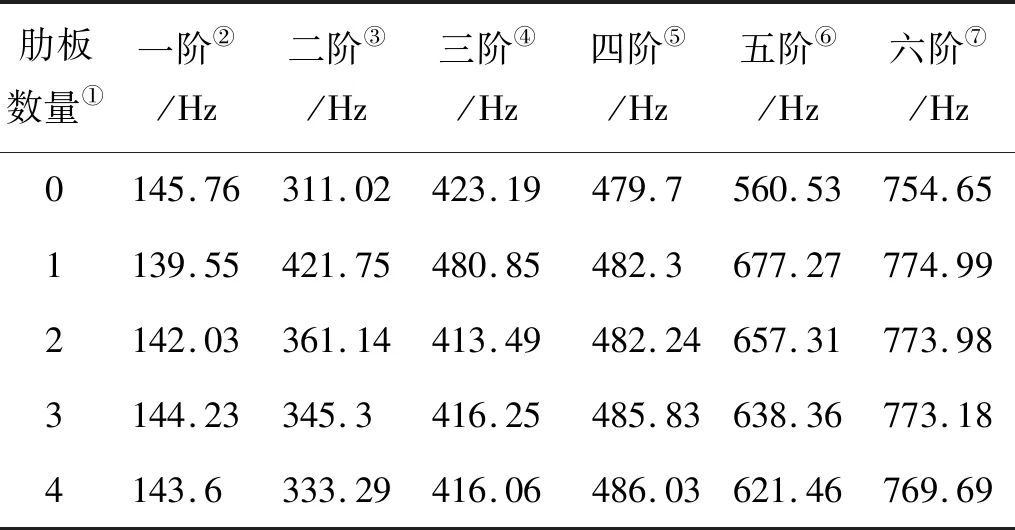
表5 不同肋板数量的加肋板固有频率Table 5 The natural frequency of stiffened plate with different number of ribs

Note:①Number of ribs;②First order;③Second order;④Third order;⑤Forth order;⑥Fifth order;⑦Sixth order

表6 不同肋板数量的加肋板刚度比Table 6 The stiffness ratioof stiffened plate with different number of ribs

Note:①Number of ribs;②Dynamic stiffness;③Dynamic stiffness ratio;④Maximum deformation;⑤Reciprocal of maximum deformation;⑥Static stiffness ratio

依据结构动力学相关理论，对表6仿真数据进行处理，绘制静态刚度对比图与动态刚度对比图，见图6。

从图6可以看出，单肋板具有最大的动静态刚度，和等质量单肋板相比，增加肋板数量并不能提高肋板结构刚度，由式(1)可知，在同等肋板质量下，增加肋板高度对转动惯量的增加远大于增加肋板数量的增加效果。

图6 肋板数量对刚度比的影响Fig.6 Influence of stiffness ratio of rib number

3.2 肋板位置对结构刚度的影响

进一步计算相同质量的情况下，肋板位置对加肋板静、动态刚度的影响，肋板尺寸为3 mm×12 mm，肋板位置按照距离受载中心0、30、60、90 mm变化共4组数据。肋板位置及载荷见图7。

图7 肋板位置示意图Fig.7 The sketch map of rib position

加肋板基本尺寸为250 mm×250 mm，厚度为3 mm，采用二次六面体单元进行网格划分，利用有限元软件计算肋板的前六阶频率值，进一步计算加肋板最大变形量及静、动态刚度比，计算结果见表7、8。

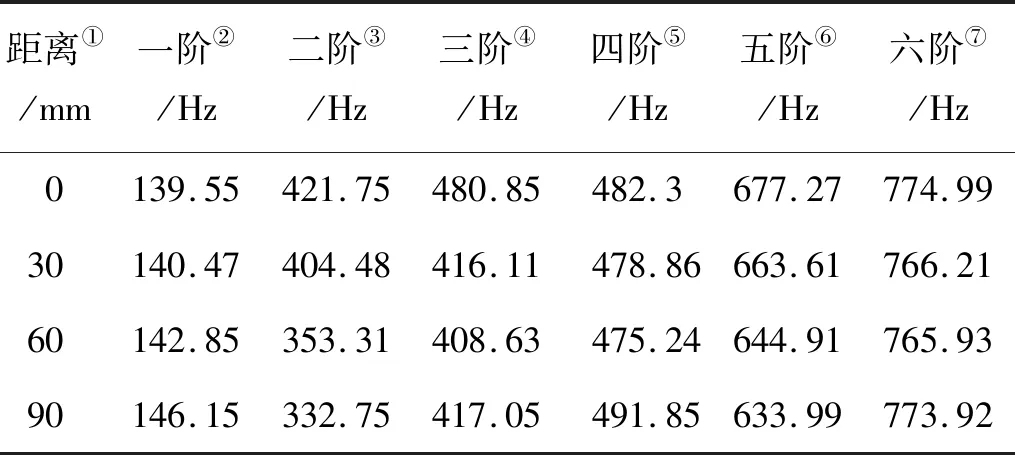
表7 肋板不同位置的加肋板固有频率Table 7 The natural frequency of stiffened plate with different positions of the rib

Note:①Distance;②First order;③Second order;④Third order;⑤Forth order;⑥Fifth order;⑦Sixth order

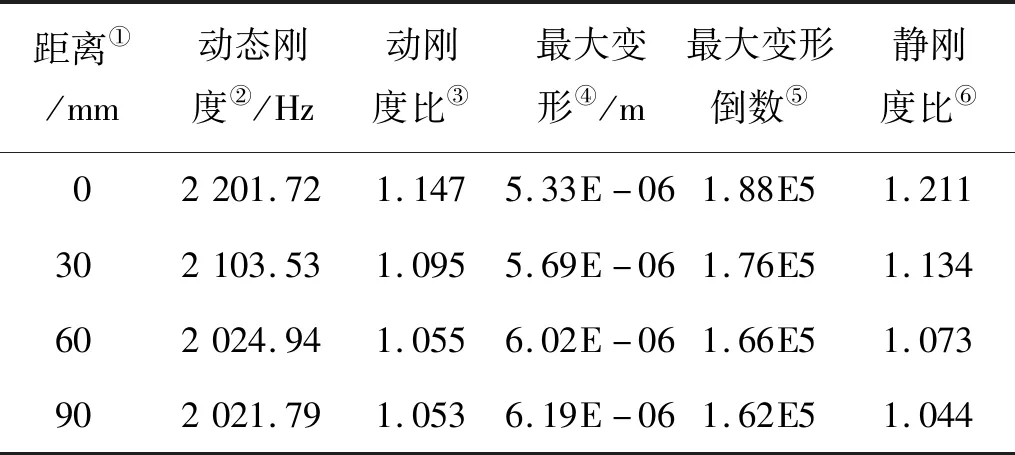
表8 肋板不同位置的加肋板刚度比Table 8 The stiffness ratio of stiffened plate with different positions of the ribs

Note:①Distance;②Dynamic stiffness;③Dynamic stiffness ratio;④Maximum deformation;⑤Reciprocal of maximum deformation;⑥Static stiffness ratio

依据结构动力学相关理论，对表8仿真数据进行处理，绘制静态刚度对比图与动态刚度对比图，如图8所示。

图8 肋板位置对刚度比的影响Fig.8 Influence of stiffness ratio of rib position

从图8中可以看出，随着肋板远离受载中心，同种规格的肋板对平板的加强作用越来越小，肋板位于激励力处对平板刚度增强的贡献最大，图6中肋板数量为3的加肋板刚度比高于肋板数量为2的加肋板刚度比，原因在于肋板数量为3的加肋板在肋板中心处有刚度加强。因此，在设计肋板时，肋板数量增加对响应影响有限，肋板位置应该位于激励力位置处。

4 结论

本文采用有限元的方法对比分析了肋板结构参数对加肋板结构刚度特征的影响规律，结果表明：

(1)肋板的结构参数与加肋板结构的静、动态刚度呈现非线性关系，其中肋板的高度参数对结构刚度的影响最为显著。

(2)纵向肋板在板厚2～4倍高度时对静态刚度的增强效果最大。

(3)随着肋板的位置逐渐偏离受载中心，肋板对结构刚度的影响逐渐减小。

(4)肋板数量增加对刚度影响有限。

在设计加肋板时，肋板位置应该位于激励力位置处；和等质量单肋板相比，在激励力作用处增加肋板高度对刚度的影响效果大于增加肋板数量，这对广泛采用板式结构形式的机械产品的结构设计具有一定的参考价值。