基于黄金比例遗传算法的动车组列车节能优化研究
汤旻安,王茜茜
基于黄金比例遗传算法的动车组列车节能优化研究
汤旻安,王茜茜
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
为研究注重最小化能耗的动车组列车运行控制,针对列车单质点模型受力分析不准确问题,提出一种对附加阻力进行处理的多质点方法,进而以多质点模型为基础进行2次优化。为解决遗传算法寻优时容易陷入局部最优的问题,提出一种基于黄金比例遗传算法的优化方法,1次优化通过该算法为列车运行寻求一组满足约束条件的目标速度集合,获得列车节能运行速度曲线。考虑过电分相对列车运行的影响,进行2次优化,将运行区间划分为操纵固定段和操纵可优化段,并通过黄金比例遗传算法搜索出一组操纵可优化段内满意的工况转换点,结合1次优化得到列车最终运行曲线。以兰考南-开封北线路CRH3型动车组为仿真实例,列车运行能耗降低了10.83%,表明所提方法是可行的。
黄金比例;遗传算法;动车组列车;电分相;节能优化

动车组列车运行能耗是其运营经济性的重要影响因素,但在列车速度提高的同时,能耗越来越大,因此,如何在满足列车运行各项约束的条件下,最大限度地节省能耗,对我国高速铁路可持续发展具有重要意义[1]。对于列车节能操纵,Howlett等[2-4]使用极大值原理搜寻关键转换点,得到了问题的最优解,并指出当限速值低于列车巡航速度时,列车贴限速行驶是一种最节能的操纵方式。Khmelnitsky[5]优化了不同线路条件下的列车控制,李玉生等[6]提出坡道三分手柄级位变化原则,使用遗传算法解决了列车手柄级位和列车位置的关系。近年来,对于高速动车组列车的研究也越来越多,Sicre等[7]仅在列车中途运行过程使用优化算法得到运行控制策略,节能效果显著。刘建强等[8]求得列车运行能耗最低时的最高速度,从而得到能量消耗最低时的操纵工况转换点。Sandidzadeh等[9]建立多质量列车模型,用蚁群算法和遗传算法解决了列车节能问题。曹佳峰等[10]提出了坡道运行优化和全线惰行优化的2阶段优化方法,达到了节能运行之目的。此外,牟瑞芳等[11-13]也对高速列车的节能问题进行了研究。对于列车节能问题,国内外学者已经做了大量研究并取得了诸多成果,但还存在以下问题:现有的列车运动学模型多为单质点模型,造成列车受力分析不准确,影响能耗的计算;控制方法大多是改进控制策略,然后对列车运行曲线进行一次的优化,鲜有再次进行优化的;很少考虑电分相对列车运行过程的影响。基于以上不足,本文提出一种以多质点列车模型为基础的2次优化策略,同时提出一种基于黄金比例遗传算法的优化方法来解决遗传算法寻优时容易陷入局部最优的问题。第1次优化利用黄金比例遗传算法寻求一组列车节能运行的速度序列,产生一条节能速度曲线,然后考虑电分相对列车运行的影响,进行2次优化,利用该算法为列车运行操纵可优化段寻求一组满意的操纵工况转换点,结合1次优化得到列车最终运行曲线,指导列车运行。
1 列车运行过程分析
1.1 受力分析
如图1所示,列车在运行期间,受牵引力t,制动力b,基本阻力0和线路附加阻力d共同作用,其牵引/制动性能由列车牵引/制动特性、编组质量和运行阻力共同决定。
列车在运行过程中受到的牵引力与制动力分别根据相应车型的牵引与制动特性曲线进行计算。
列车基本运行阻力影响因素复杂,通常用经验公式计算:
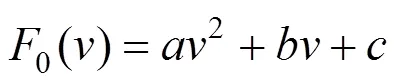
式中:为列车速度;,和为基本阻力系数。
真实反映列车的受力,对研究列车运行能耗及优化结果的准确性有直接影响,因此本文用多质点模型建立列车运动方程。多质点模型将每一节列车视为一个质点,当经过线路断面变化点时,对每节列车分别计算附加阻力,更加符合实际运行情况,计算结果更准确。

图1 列车运行受力示意图
根据将列车视为单质点附加阻力的计算[14],将列车视为多质点时,每节列车的附加阻力计算方法与单质点计算方法相同,列车所受总附加阻力为每节列车所受附加阻力之和,具体计算公式为


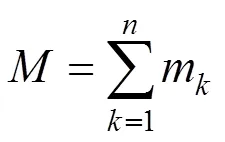
多质点模型虽使计算更准确,但列车的受力情况复杂,计算量大。而列车所受附加阻力大小只与所处的位置有关,因此为降低计算量,本文对列车附加阻力进行预先处理,将附加阻力存成一个链表,牵引计算时,由列车当前所处的位置便可得到附加阻力的大小。如表1所示,为运行区间距离,以为步长,建立附加阻力链表,取为0.01。

表1 附加阻力链表
1.2 运动方程
建立多质点附加阻力模型后,得到更加精细完整的列车运动方程,由牛顿第二定律推导得


式中:t为牵引力使用系数;b为制动力使用系数;为回转质量系数。
根据运动方程可计算列车运行速度、距离和时分。
2 一次优化模型的构建
列车节能运行的最佳控制原则为最大牵引、匀速、惰行和制动[15],下文的控制策略分析均以此原则为基础展开。
2.1 区间划分

2.2 节能目标函数的建立
先采用反向迭代法确定列车开始制动时的位置x,从运行终点反推制动速度轨迹,获得制动距离d和制动时间b。为满足运行需求,牵引力和制动力由t和b进行调节。

因此到达目标速度前列车运行时间和距离为:


到达目标速度后运行时间和距离为:


式中:d为子区间的间距。


式中:为能耗利用率。

设b在第个坡道,第个子区间起点到线路终点为制动区间。列车以v-1匀速运行至x点后,开始制动。制动加速度a由操纵经验给定。
制动前匀速运行的时间和距离为:


匀速运行的列车能耗:

制动运行的时间和距离为:
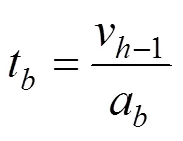

制动运行时列车储能:
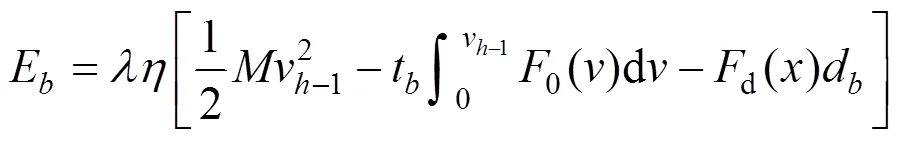
式中:为再生制动能量利用率。
因此建立1次优化目标函数:

为保证运行期间的安全、准点及精确停车,有约束条件:

用惩罚函数将原问题化为无约束问题:


式中:1,2,3和4为惩罚因子。
2.3 用黄金比例遗传算法进行优化
设计一种黄金比例遗传算法来解决遗传算法求解速度慢且容易陷入局部最优的问题。黄金比例是一个数学比例关系,体现事物的内在和谐与平衡[17],使用对称和相等收缩的方法来逐渐缩小搜索范围,解空间每次减小到0.382或0.618倍,利用其强大的局部优化优势找到2个局部最优个体间的更优的个体。
用黄金比例遗传算法对列车运行进行1次优化的流程图如图2所示。
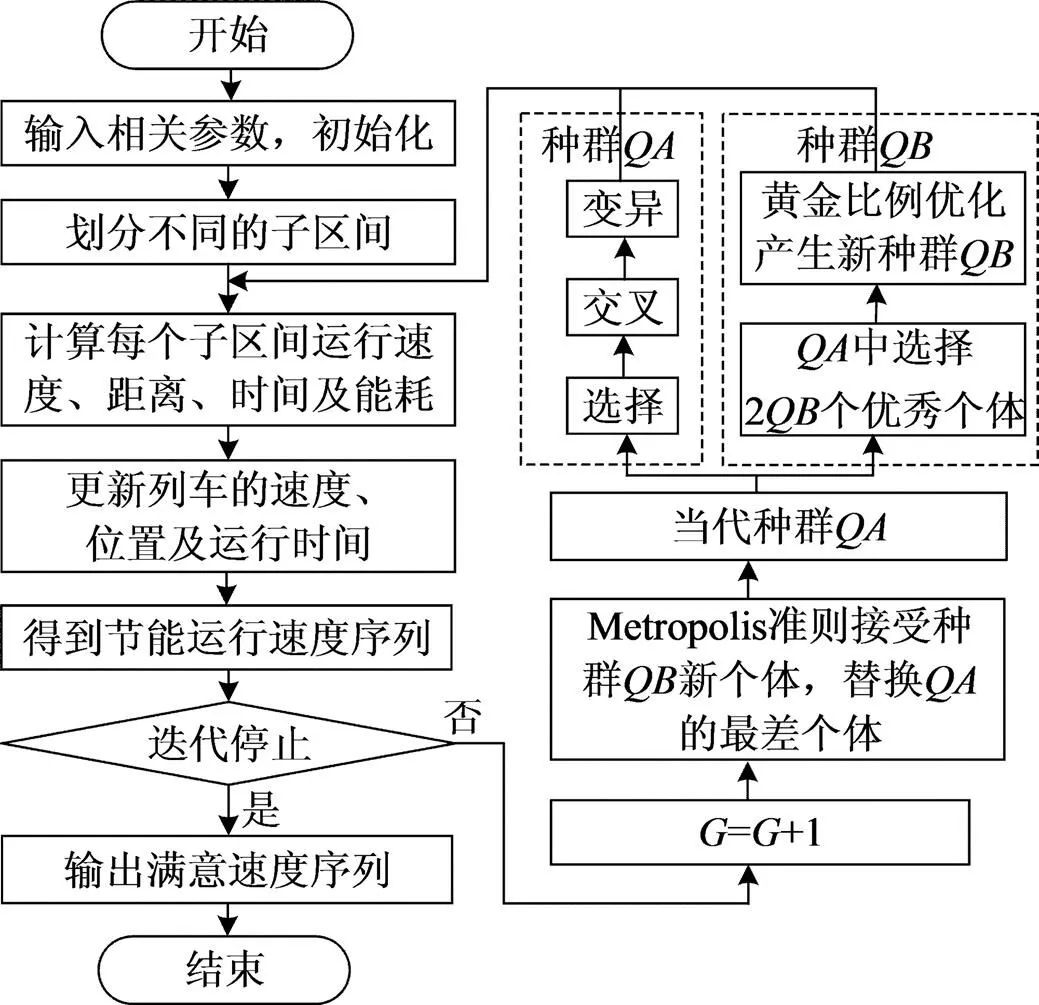
图2 一次优化流程图
2.3.1 染色体编码及解码
采取实数编码,目标速度序列为:

2.3.2 初始种群产生
初始种群和由一定数量的染色体随机产生。是遗传算法全局优化的主种群,是黄金比例局部优化的子种群。
2.3.3 适应度函数
取目标函数的倒数为适应度函数:

式中:为调整系数。
2.3.4 个体接受准则
采用Metropolis准则概率接受中的新个体,中最差个体依次被接受的优秀个体替换。
2.3.5 局部优化
从每代遗传算法优化过的个体中选择最好的2个个体,替换中最差的个体,并从中选择个优秀个体作为初始个体,使用黄金比例算子执行局部优化,更新。
2.3.6 遗传算子
选择:轮盘赌法。
交叉和变异:引入黄金比例概率0.382或0.618搜索最优自适应点,提升搜索效率,加快运算。相应的交叉和变异概率为:


2.3.7 停止条件
以最大迭代次数作为停止条件。
3 2次优化模型的构建
为使列车运行节能效果更佳,且使运行情况更符合实际,因此考虑电分相对列车运行的影响,再一次进行优化。
列车过电分相时没有接触网供电,只能惰行或再生制动,假设采用惰行方式过电分相。由操纵经验知,列车在起车和进站时分别采用最大牵引和最大制动工况。因此,可以由电分相的分布和列车起停将运行区间划分为操纵固定段和操纵可优化段,如图3所示,阴影部分为操纵固定段,其余部分为操纵可优化段。由操纵特性造成的动车组能耗差异达30%[18],2次优化以操纵可优化段内工况转换点为变量,再次使用黄金比例遗传算法求解满足约束条件的操纵可优化段内的列车节能操纵序列。
3.1 区间划分


图3 操纵固定段和操纵可优化段
一次优化生成了一条速度曲线,该曲线既是限速线,又是节能线,因此可将该曲线视为2次优化的限速线。仿真运行时,当列车速度大于1次优化所得速度曲线,切换为1次优化所得节能曲线工况运行,直至运行速度低于1次优化所得速度曲线,则恢复为当前列车运行工况。
3.2 节能目标函数的建立
设一个子区间内各个工况的能耗分别为E,E,E和E,则列车在操纵可优化段的能耗为:

式中:为子区间个数。找到各工况转换点的位置,便可知列车在各工况运行的时间和距离,由运动方程可求得列车在到达各个工况时的速度,最后可求得各个工况的能耗,由于惰行阶段能耗为0,式(26)可以写为:
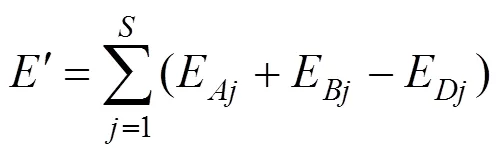
操纵固定段的能耗为:
1) 起车阶段

2) 电分相阶段

3) 停车制动阶段

综上,2次优化中的列车能耗为:

3.3 用黄金比例遗传算法进行优化
用黄金比例遗传算法对列车运行进行2次优化的部分流程图如图4所示。

图4 2次优化部分流程图
将电分相工况作为基因包含于染色体中。算法在进行交叉和变异操作时,会随机选择交叉点和变异点,当选中操纵固定段内的基因时,会产生不可行解。因此,2次优化与1次优化的黄金比例遗传算法不同之处在于:在全局及局部优化之前进行判断,使操纵固定段的基因不参与优化操作;且2次优化算法搜索的是操纵可优化段内工况转换点位置。其他步骤及参数设置均与一次优化中相同。
4 实例仿真分析
以兰考南-开封北线路为仿真实例,线路总长53 km,含23个坡道、7段曲线和2处电分相,分相区为21.379~21.772 km和46.559~46.971 km。运行时间16 min,设置时间误差30 s。选4动4拖的CRH3动车组列车,主要参数如表2所示。
将使用黄金比例遗传算法与遗传算法进行2次优化的操作各执行30次,以30次平均最优适应度值、优化时间、平均迭代次数作为评价指标,对2种算法在列车节能优化中的性能进行对比分析。2次优化的遗传算法的交叉变异概率取cmax和mmax,其他参数与黄金比例遗传算法取值相同。2次优化的黄金比例遗传算法参数取值如表3所示,对比分析结果如表4所示。

表2 CRH3主要参数特性

表3 参数取值

表4 对比分析结果
任取30次操作中的1次,观察2种算法迭代次数与最优适应度函数值的变化趋势,分别如图5和图6所示。由表4、图5及图6可知,黄金比例遗传算法比遗传算法的收敛速度更快,求解性能更优。

图5 1次优化2种算法比较
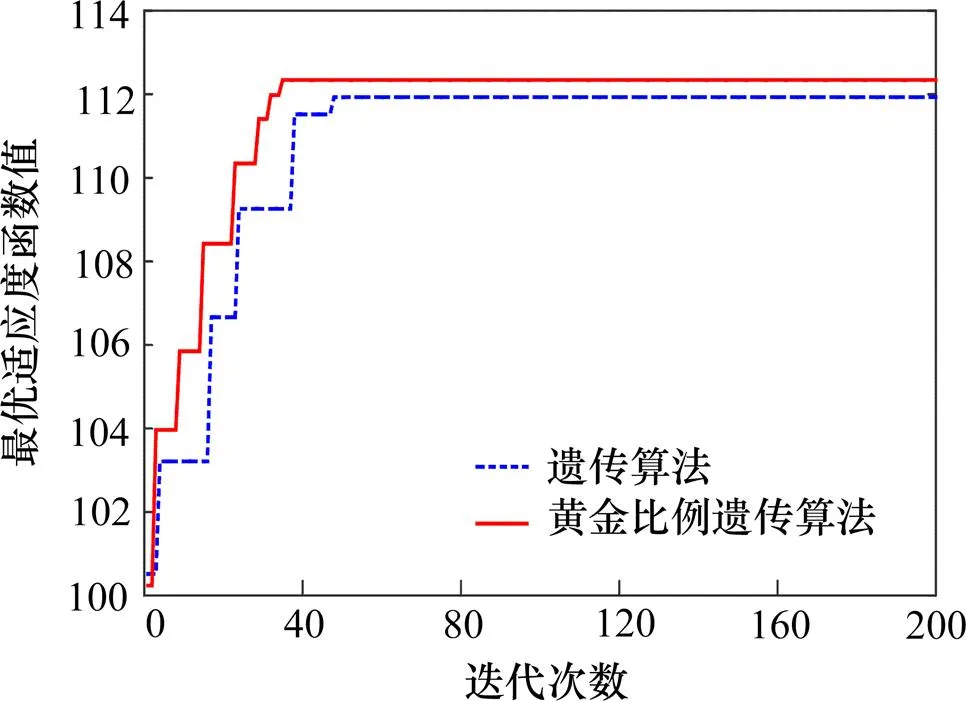
图6 2次优化2种算法比较
为比较2次优化过程的节能效果,将1次优化和2次优化所得的列车运行曲线与未采取优化措施时的列车运行曲线进行比较,如图7所示。
可以看到,未优化与1次优化在过第1个电分相时为匀速工况,1次优化在过第2个电分相时为匀速工况,均不符合列车实际运行情况;而2次优化在过2个电分相时均为惰行工况,符合列车实际运行情况。计算得3条曲线对应的运行时间与能耗如表5所示。
由图7还可看到,在16.67 km与32.62 km处2次优化运行的速度超过了1次优化运行的速度,在这2处1次优化运行的工况均为惰行工况,因此在2次优化列车运行到这2处时,切换为惰行工况,直到速度低于1次优化运行速度时,切换为原来的工况运行,列车最终运行曲线如图8所示。

图7 3条运行结果曲线

表5 运行时间与能耗

图8 列车最终运行曲线
经计算,列车沿最终运行曲线运行时,耗能810.7 kWh,运行时间为986.4 s,较2次优化多了7.2 s,这是由于惰行时间增多的缘故,但仍满足准时性要求,列车最终节能10.83%。
5 结论
1) 在注重最小化能耗的动车组列车运行控制中,针对列车单质点模型受力分析不准确问题,提出一种对附加阻力进行处理的多质点方法,使所建立的列车运动学模型更加精细完整,为能耗的计算打下基础。
2) 以多质点运动学模型为基础,进行2次优化。提出一种基于黄金比例遗传算法的优化方法来解决遗传算法容易陷入局部最优的问题。第1次优化利用该算法为列车节能运行寻求一组满意的速度序列,然后考虑列车过电分相时的运行情况,使列车运行更加符合实际,再次使用该算法寻求一组操纵可优化段内的工况转换点,最后结合2次优化得到列车最终运行曲线。
3) 由实例仿真分析可知,黄金比例遗传算法比遗传算法更有优越性,且在满足各种约束的前提下,最终节能效果为10.83%,证明所提方法是有效的。本文列车运行优化为离线优化,后续可研究在线优化,以适应多变的列车运行情况。
[1] 荀径, 杨欣, 宁滨, 等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14-20. XUN Jing, YANG Xin, NING Bin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14-20.
[2] Howlett P. An optimal strategy for the control of a train[J]. The Journal of the Australian Mathematical Society Series B Applied Mathematics, 1990, 31(4): 454-471.
[3] Pudney P, Howlett P. Optimal driving strategies for a train journey with speed limits[J]. The Journal of the Australian Mathematical Society Series B Applied Mathematics, 1994, 36(1): 38-49.
[4] Howlett P. The optimal control of a train[J]. Annals of Operations Research, 2000, 98(1/4): 65-87.
[5] Khmelnitsky E. On an optimal control problem of train operation[J]. IEEE Transactions on Automatic Control, 2000, 45(7): 1257-1266.
[6] 李玉生,侯忠生. 基于遗传算法的列车节能控制研究[J]. 系统仿真学报,2007,19(02):384-387. LI Yusheng, HOU Zhongsheng. Study on energy-saving control for train based on genetic algorithm[J]. Journal of System Simulation, 2007, 19(2): 384-387.
[7] Sicre C, Cucala A P, Fernández A, et al. Modeling and optimizing energy-efficient manual driving on high-speed lines[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2012, 7(6): 633-640.
[8] 刘建强, 魏远乐, 胡辉. 高速列车节能运行优化控制方法研究[J]. 铁道学报, 2014, 36(10): 7-12. LIU Jianqiang, WEI Yuanle, HU Hui. Research on optimization control method of energy-saving operation of high-speed trains[J]. Journal of the China Railway Society, 2014, 36(10): 7-12.
[9] Sandidzadeh M A, Alai M R. Optimal speed control of a multiple-mass train for minimum energy consumption using ant colony and genetic algorithms[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2017, 231(3): 280-294.
[10] 曹佳峰, 刘斌. 基于2阶段优化的高速列车节能运行仿真研究[J]. 铁道科学与工程学报, 2018, 15(4): 821-828. CAO Jiafeng, LIU Bin. Research on simulation for energy-saving operation of high-speed trains based on two-stage optimization[J]. Journal of Railway Science and Engineering, 2018, 15(4): 821-828.
[11] 牟瑞芳, 肖琴杰. 基于速度集的高速动车组运行能耗优化操纵模型及算法[J]. 中国铁道科学, 2014, 35(3): 107-112. MOU Ruifang, XIAO Qinjie. Optimized control model and algorithm based on speed set for operation energy consumption of high speed EMU[J]. China Railway Science, 2014, 35(3): 107-112.
[12] 梁志成, 王青元, 何坤, 等. 基于极大值原理的电动车组节能操纵[J]. 铁道学报, 2015, 37(10): 16-25. LIANG Zhicheng, WANG Qingyuan, HE Kun, et al. Energy saving control of electric multiple unit train based on maximum principle[J]. Journal of the China Railway Society, 2015, 37(10): 16-25.
[13] SONG Yongduan, SONG Wenting. A novel dual speed- curve optimization based approach for energy-saving operation of high-speed trains[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(6): 1564- 1575.
[14] 彭俊彬. 动车组牵引与制动[M]. 北京: 中国铁道出版社, 2009. PENG Junbin. Traction and braking of EMU[M]. Beijing: China Railway Press, 2009.
[15] 王青元. 高速列车准点节能优化操纵研究[D]. 成都: 西南交通大学, 2017. WANG Qingyuan. Energy-efficient control of high-speed trains considering punctuality constraint[D]. Chengdu: Southwest Jiaotong University, 2017.
[16] 宋文婷, 谭觅, 蔡文川, 等. 高速列车的节能操纵策略研究[J]. 铁道科学与工程学报, 2016, 13(3): 423-429. SONG Wenting, TAN Mi, CAI Wenchuan, et al. Research on energy-saving operation strategy for high-speed train[J]. Journal of Railway Science and Engineering, 2016, 13(3): 423-429.
[17] 杨文臣, 张轮, 饶倩, 等. 基于黄金分割点遗传算法的交通信号多目标优化[J]. 交通运输系统工程与信息, 2013, 13(5): 48-55. YANG Wenchen, ZHANG Lun, RAO Qian, et al. Multi-objective optimization for traffic signals with golden ratio based genetic algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(5): 48-55.
[18] 张芮. 铁路运输企业能耗指标监测与评价方法研究[D]. 成都: 西南交通大学, 2012. ZHANG Rui. Research on monitoring and evaluation methods of energy consumption index of rail transportation enterprises[D]. Chengdu: Southwest Jiaotong University, 2012.
[19] 纪云霞. 列车节能运行优化的改进遗传算法研究[D]. 成都: 西南交通大学, 2018. JI Yunxia. Study on improved genetic algorithm for train energy-saving operation optimization[D]. Chengdu: Southwest Jiaotong University, 2018.
Research on energy-saving optimization of EMU trains based on golden ratio genetic algorithm
TANG Minan, WANG Qianqian
(School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
In order to study EMU (electric multiple units) trains operation control with attention to minimizing the energy consumption, a multi-particle method to deal with additional resistances was proposed aiming at the problem that the force analysis of single-particle model for the train was inaccurate, and two optimizations were carried out based on the multi-particle model. Then, a method with golden ratio genetic algorithm was proposed to solve the problem that genetic algorithm was easy to fall into local optimum, by which a set of target speed sets satisfying constraints were sought for the train in the first optimization, thus the train energy-saving operation speed curve was determined. Considering the influence of electrical phases for the train operation, the second optimization was carried out. The operation interval was divided into fixed segments and optimizable segments of manipulation, and a set of satisfactory operation switching points were searched by golden ratio genetic algorithm. The final operation curve of the train was obtained in tandem with the first optimization. Taking CRH3of Lankao South-Kaifeng North line as a simulation case, the energy consumption of the train operation is reduced by 10.83%, which shows that the proposed method is feasible.
golden ratio; genetic algorithm; EMU trains; electrical phases; energy-saving optimization
10.19713/j.cnki.43-1423/u. T20190398
U268
A
1672 - 7029(2020)01 - 0016 - 09
2019-05-13
国家自然科学基金资助项目(61663021,61861025,61763025);甘肃省高校科研项目(2017A-025)
汤旻安(1973-),男,陕西勉县人,教授,博士,从事智能交通控制研究;E-mail:tangminan@yahoo.com
(编辑 阳丽霞)

