分幅距离对青藏高速公路分离式路基动力响应的影响

赵涛，梁庆国，王育红，陈拓，王燕

分幅距离对青藏高速公路分离式路基动力响应的影响

赵涛1, 2，梁庆国1，王育红2，陈拓3，王燕4

(1. 兰州交通大学 土木工程学院，甘肃 兰州 730070；2. 陕西铁路工程职业技术学院，陕西 渭南 714000；3. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116；4. 青海大学 土木工程学院，青海 西宁 810016)

为研究地震波作用下分离式路基的动力响应特性，结合现场钻孔资料，以标准断面的分离式路基为研究对象，采用二维非线性动力有限元非关联流动法，建立2幅坡脚距离分别为5，10，15和20 m的路基模型。通过施加50 a超越概率2%，10%和63%的地震波，得到分幅距离变化对路基地震动力响应的影响效应。研究结果表明：路基表面的Mises 应力值大小受坡脚距离变化影响较大，对天然地表与坡脚影响微小，而对剪应力12值大小的影响规律与此相反；随着坡脚距离的增加，路基表面与天然地表的水平峰值位移呈现先升高后降低的变化规律，在10 m坡脚距离的参考点水平峰值位移出现极大值。研究结果为青藏工程走廊内的路基选型布线与抗震设计提供一定参考。

青藏工程走廊；分离式路基；分幅距离；地震波；动力响应

中国多年冻土面积多达2.15万平方公里，约占领土面积的22.3%，仅次于俄罗斯、加拿大，居世界第三[1]。而且我国高海拔多年冻土面积达1.73万平方公里，高居世界之最。温度极低、面积极广、厚度极大的青藏高原多年冻土区，北起昆仑山北坡，南至喜马拉雅山北坡，总面积占我国多年冻土区域面积的70%左右[2]。青藏工程走廊是西藏地区发展的重要战略通道，在狭长的走廊内聚集多项已有国家重点设施以及规划修筑的青藏高速公路工程等[3]。多年冻土的稳定与人类社会生存发展息息相关，青藏高速公路是通往拉萨的重要“生命之线”，全长大约1 900 km，是京藏高速公路(G6国道)重要的一部分。青藏工程走廊内已建成既有铁路和公路路基幅宽相对比较狭窄，但青藏高速公路的路基幅宽会倍增，随之路基的吸热能力会急剧升高，导致冻土区退化速率和范围增大，将对天然冻土的扰动加大[4]。路基宽度的变化将会直接影响冻土路基强度，传热过程以及力学稳定性。已有宽幅路基研究主要集中于温度效应领域的分析：YU等[5-6]针对结构变化和气候变暖情况进行路基热动态分析；王英才[7]选取寒区路基温度场受路基宽度值变化的影响开展针对性研究；在高海拔多年冻土地区修筑高等级公路，马巍等[8-9]考虑横向热影响范围，提出高速公路热学稳定性预估和布线设计，并推荐青藏高速公路修建于青藏铁路同侧；分幅距离越小，对冻土路基的热干扰越大[10]；汤涛[11-12]对青藏高速公路宽幅路基有关温度效应特性及降温措施开展数值模拟研究。同时，青藏工程走廊位处当今中国大陆地壳构造运动最为强烈区域，区内活断层规模巨大、分布密集，地震活动频繁、震级高[13]，其已对青藏工程走廊内的众多重要构筑物构成破坏或潜在威胁。有关窄幅路基动力响应方面，董连成[14]开展了路基动稳定性评估；LI等[2, 15-16]通过数值模拟，就地震动力环境下青藏铁路类窄幅路基的动力特性进行了探究分析。以上高原路基建设考虑温度效应方面和窄幅路基抗震方面的研究，可为青藏工程走廊修筑宽幅路基提供一定参考。然而，青藏高速公路因地形条件限制，宽幅路基极易吸热，昼夜温差大，多年冻土极为温度敏感等诸多因素，部分特殊区间可考虑选用分离式路基布线类型。加之该区高等级公路受潜在地震威胁影响显著，对于路基抗震和动力响应方面研究不容忽视。因此，考虑不同分幅距离工况的青藏高速公路分离式路基，受地震波作用下动强度和动力响应变化规律性质，已是勘察设计人员和施工技术人员必须重视及迫切解决的问题。鉴于此，本文在现场钻孔试验的基础上，选用二维非线性动力有限元非关联流动法，分别建立了4种分幅距离工况的左右幅分离式路基标准横断面模型，通过施加多年冻土区3种强度的地震波，得到分幅距离变化对路基的地震动力响应影响效应。

1 分离式路基模型建立

1.1 扩展摩尔库仑模型

土工数值计算学科范畴针对岩土类相关有限元数值模拟普遍选用Mohr-Coulomb强度准则，图1[17]给出了M-C屈服面、R屈服面、T屈服面、D-P屈服面以及Mises屈服面在子午面和π平面上的形状及相对关系。由图可观察出M-C屈服面存有不光滑的尖角，基于有限元数值模拟，如若计算选用相关联流动法则，塑性流动方向不唯一现象将会出现在尖角处，从而使数值计算程序复杂且收敛较慢甚至无法收敛。因此，使用扩展M-C屈服准则[18]，采用非关联流动法可较好地解答上述难题。

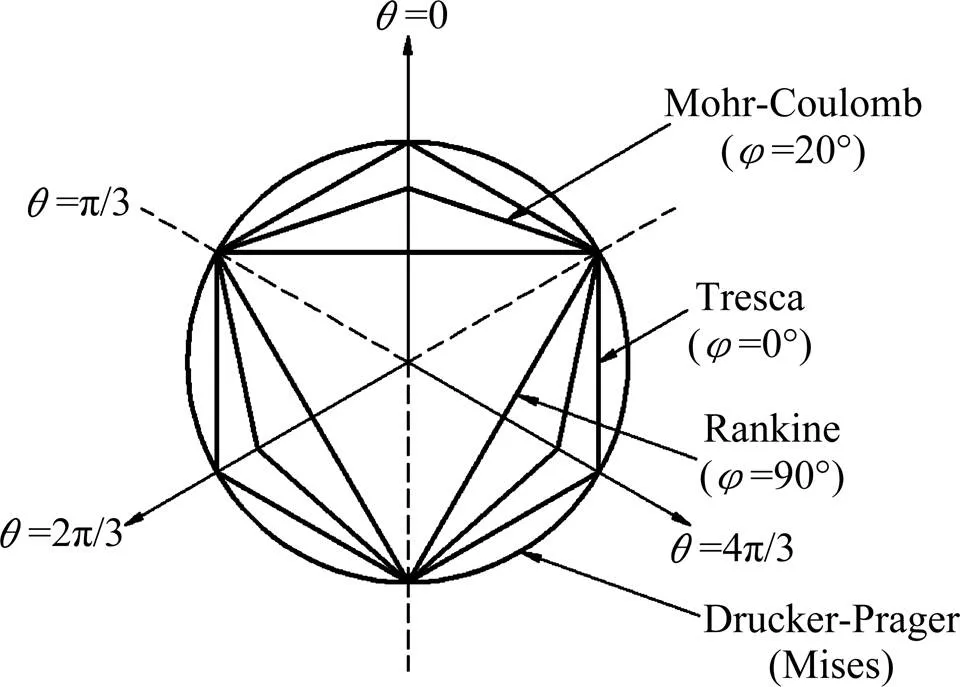
图1 Mohr-Coulomb模型中的屈服面

1) 屈服面

Mohr-Coulomb屈服面函数见式(1)所示。

式中：R值决定着屈服面在π平面的形状，是等效剪应力；是平均主应力；是土的内摩擦角；是土的黏聚力。

2) 塑性势面

塑性势面选择光滑且连续的椭圆公式，见式(2)。

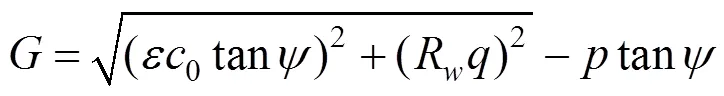
式中：R值决定着在π平面的形状，是剪胀角；0是初始黏聚力；是子午面偏心率，决定着在子午面的形状。

因此，本着解决在有限元模拟过程中塑性流动方向不唯一现象，减弱土体的剪胀效应，进而解决计算程序繁冗与数值计算结果不收敛难题，遵从线弹性模型和摩尔库仑模型相结合的非关联流动法则，在ABAQUS有限元数值软件中，基于二维非线性动力有限元非关联流动法，开展不同分幅距离条件下分离式路基的动力响应计算。

1.2 模型尺寸

参考已运营的京藏高速(G6)京格段，图2给出青藏高速分离式路基计算模型。选用路基宽度12 m，路面材料均为沥青混合料，路基高4.8 m，路基坡度比选用1:1.5，路面横坡度为2.0%。计算工况中，双幅内坡脚之间距离用S代表，S分别取值5，10，15和20 m，即代表两线间距分别为31.4，36.4，41.4和46.4 m。沿着路基模型对称轴位置的4个参考点：A代表路基表面，B代表天然地表，C代表埋深为2 m处，D代表埋深为5.9 m处。

图2 青藏高速公路分离式路基

1.3 填筑材料及计算工况

表1汇总出分离式路基计算模型的填筑材料和地基土体的物性参数指标，选取依据是北麓河现场钻孔取样试验及参考文献[19]。考虑到动力计算中地震波在边界处的反射影响，地基模型两侧采用无限元边界来减小边界效应，并在底部设置固定边界。路基填料及地基土层的单元均选用平面应变式有限元单元，而地基两侧布设平面应变式无限元单元。动力计算分析过程中，第1步设置自重应力分析步，得到路基模型的初始应力条件，再将其施加于模型结构；第2步设置动力计算分析步，选用采样间隔为0.02 s，50 a超越概率2%，10%和63%强度的3种地震波加速度时程，曲线如图3所示，其加速度峰值分别为252，150和51 cm/s2。在模型基岩处依次施加这3种地震波，对4种分幅距离工况下的分离式路基进行动力响应分析。

表1 填筑材料物性参数

(a) 50 a超越概率2%；(b) 50 a超越概率10%；(c) 50 a超越概率63%

2 动力响应特性

基于ABAQUS有限元软件，通过二维非线性动力有限元非关联流动法，施加3种强度地震波，研究了不同分幅距离工况下路基模型的加速度放大系数、应力响应特性及位移响应特性的影响 结果。

(a) 坡脚距离5m；(b) 坡脚距离10m；(c) 坡脚距离15m；(d) 坡脚距离20m

2.1 加速度放大系数

地震动力荷载作用的加速度响应研究，通常选择加速度放大系数作为研究量值。首先，定义加速度放大系数为参考点加速度时程曲线的峰值和模型基底输入的加速度时程峰值之比。图4给出4种坡脚距离工况下路基在竖直方向上A，B，C和D参考点的加速度放大系数变化曲线。由图总体对比可知，随着输入地震波加速度时程强度大小的增加，模型参考点加速度放大系数表现出减小走势。地震波在地基层的加速度放大系数变化曲线很接近，表现出受地震波强度大小的影响微小；然而地震波在路基本体中不断扩散传播，放大系数曲线变化差异较为明显，这与2幅路基的修筑位置距离有关，修筑距离越近对于波的传播反射现象愈加明显。同时，加速度放大系数沿着竖直方向向上，不同坡脚虽略有微小差别但全部呈现出放大现象。

图5柱形图汇总了4种分幅距离工况下模型4个参考点加速度放大系数值。对路基本体而言，路基表面A点和天然地表B点的加速度放大效应有着随地震强度值大小的增大而逐渐减小规律。对地基土层埋深处而言，C和D点的加速度放大效应随分幅距离复杂多变，可能和路基不同修筑形式改变了地基层的固有振动频率有关。修筑10 m坡脚距离路基，施加63%地震波加速度时程，天然地表与路基表面的加速度放大效应较小，加速度放大系数数值为3.7和5.3；而施加10%和2%地震波加速度时程，天然地表与路基表面的加速度放大效应较大，天然地表放大系数数值是5.4和4.8；路基表面放大系数数值是6.4和4.7。

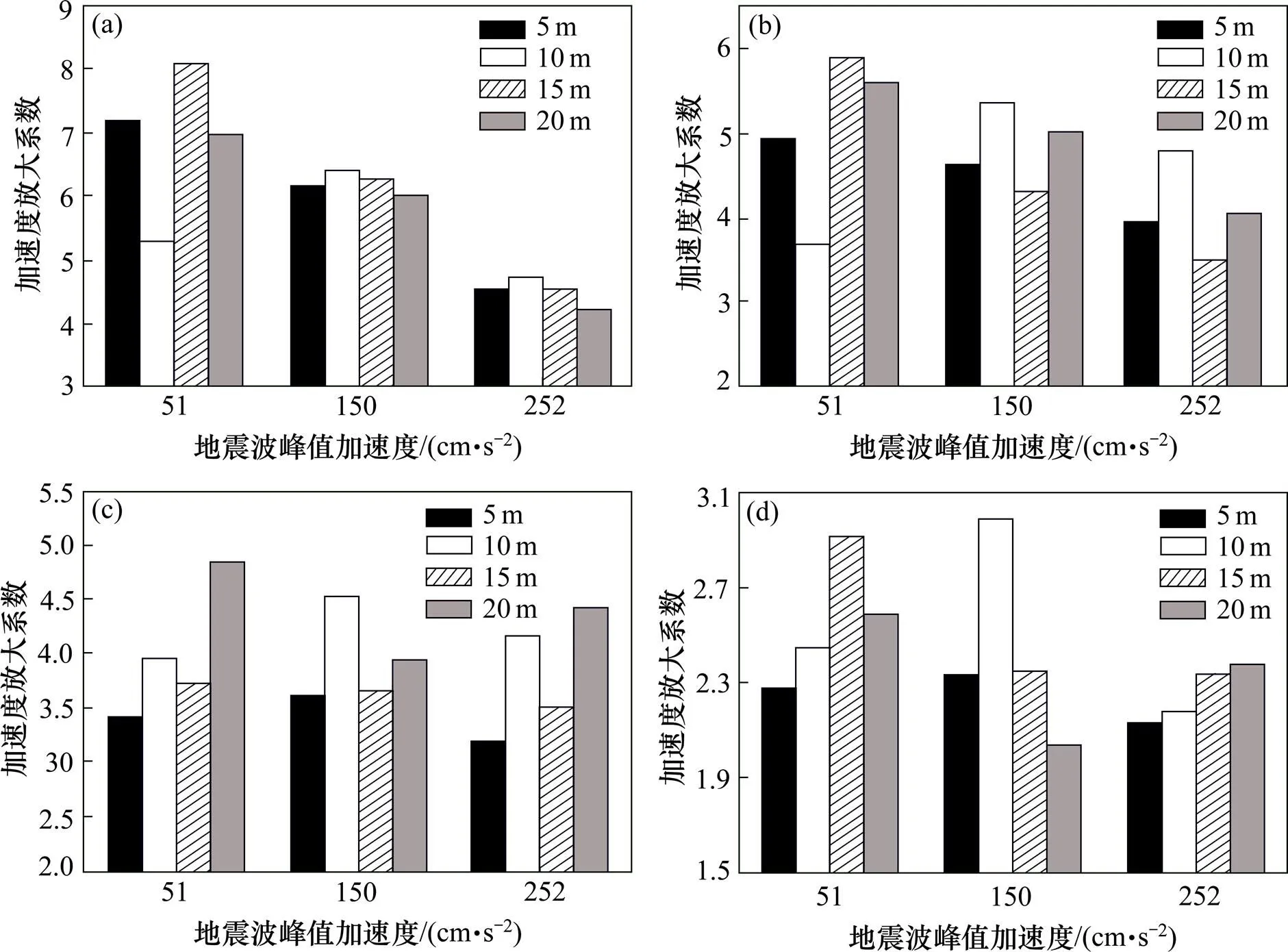
(a) 路基表面A点；(b) 天然地表B点；(c) 地基深2 m C点；(d) 地基深5.9 m D点

2.2 应力响应特性

分离式路基的动应力响应变化特性，此处仅以超越概率10%的地震波加速度时程的工况为例，进行动应力变化分析。选择路基表面A点、天然地表B点、坡脚F为研究参考点，在模型上提取参考点的Mises应力和剪应力S12随时间变化的波形时程变化曲线。首先对Mises应力变化曲线的各数值求取平均值，然后绘制图6所示参考点的Mises 应力平均值和坡脚距离的变化关系图。从图6可看出，Mises 应力平均值的大小在路基表面较大，其次是天然地表，坡脚较小。同时，随着坡脚距离的增大，Mises 应力平均值变化幅度在A点多达22.8 kPa；B点变化幅度仅为5.8 kPa；C点变化幅度仅为5.7 kPa。由此可认为，坡脚距离的增加对路基表面的Mises 应力的平均值变化有较大影响，对天然地表和坡脚应力平均值有很微小影响。为便于比较，图6中的虚线代表在同等地层条件下24 m单幅宽路基相应参考点的Mises应力值平均值。对于分离式路基Mises应力值，在路基表面大于整体式路基(其值为95.5 kPa)，在天然地表略大于整体式路基(其值为60.3 kPa)，在坡脚略小于整体式路基(其值为46.0 kPa)，可认为路基的分离式布设，会增大路基表面、天然地表以及减小坡脚的Mises 应力值。

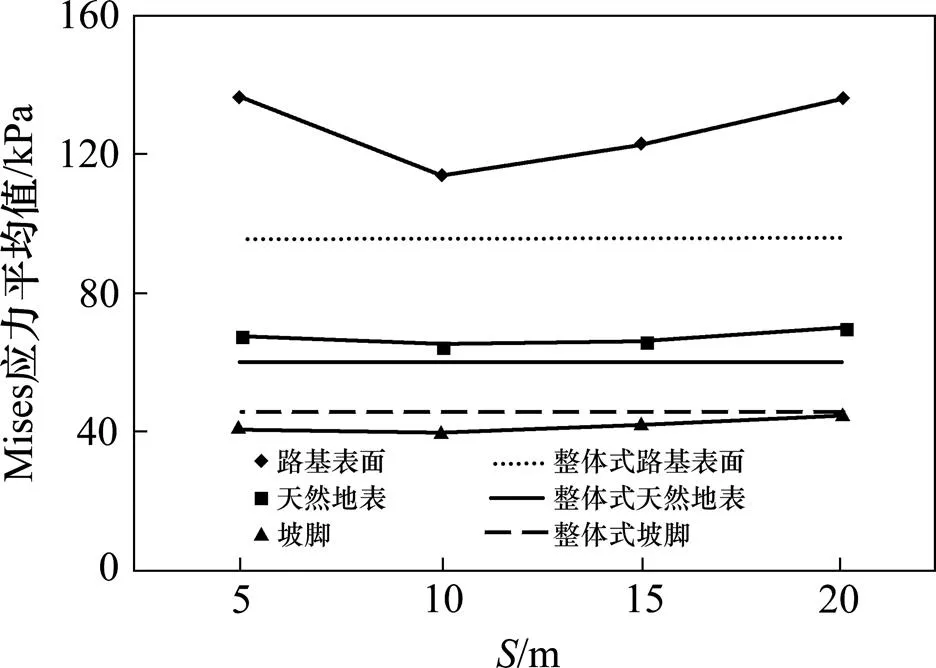
图6 Mises 应力平均值和坡脚距离之间关系图

对剪应力S12变化曲线的各数值取绝对值，然后再得到平均值，绘制图7所示参考点的剪应力S12绝对变化量平均值和坡脚距离的变化关系图。从图7可以看出，剪应力S12绝对变化量平均值的大小在天然地表是较大的，坡脚值接近天然地表，路基表面是较小的。随着坡脚距离的增大，S12绝对变化量平均值变化幅度在A点仅是0.5 kPa；B点变化幅度为5.8 kPa；C点变化幅度为2.2 kPa。可认为，坡脚距离的增加对路基表面剪应力的影响较小，对天然地表和坡脚的影响较大。为便于对比，图7中虚线代表同等地层分布条件下24 m单幅宽路基相对应参考点的剪应力S12的绝对变化量平均值。对分离式路基S12值而言，在天然地表小于整体式路基(其值为20.7 kPa)，在坡脚较小于整体式路基(其值为17.7 kPa)，在路基表面略大于整体式路基(其值为2.8 kPa)，可认为路基的分离式布设，会减小天然地表、坡脚以及微增大路基表面的剪应力值。

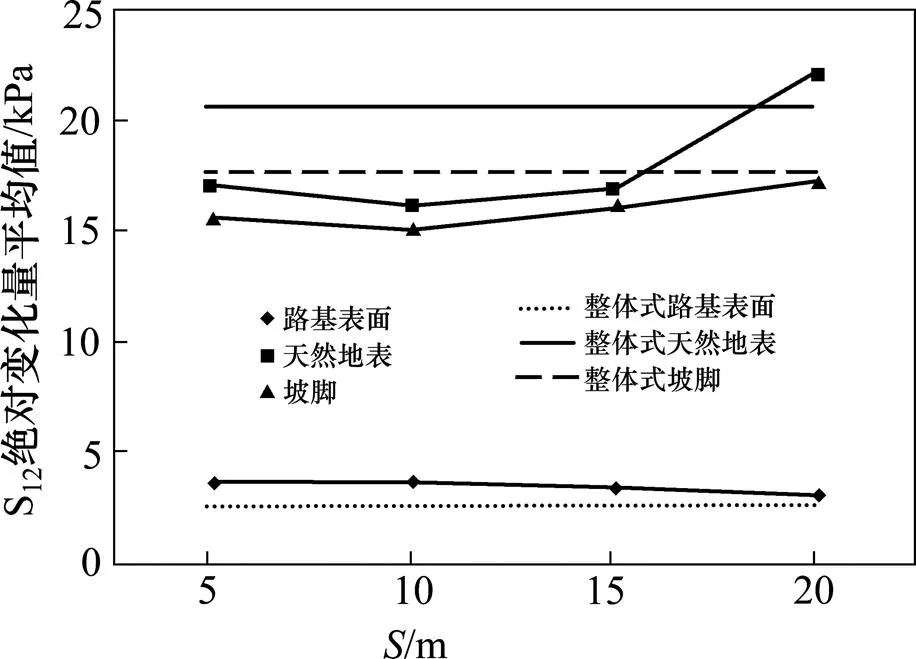
图7 S12绝对变化量平均值和坡脚距之间关系图

(a) 50 a超越概率2%；(b) 50 a超越概率10%；(c) 50 a超越概率63%

2.3 位移响应特性

考虑地震荷载施加位置为模型底部，即图2中冻结泥岩底层代表基岩处，地震波的输入方向为水平向，进而比较不同强度地震波作用，重点分析路基水平方向位移变化特征。参考点A，B，C和D的水平位移用绝对位移表示，首先提出参考点和模型底部E点的水平方向的位移时程曲线，然后计算其差值作为参考点的水平绝对位移时程曲线，最后在该曲线上筛选出参考点的水平位移峰值1，示意性给出坡脚距离为10 m工况下路基表面A点的水平位移1时程曲线，如图8所示。图9给出施加地震加速度时程，4种分幅距离工况的路基参考点的水平峰值位移变化图。由图可知，不同分幅距离参考点的水平峰值位移1的呈增大走势，即沿着模型垂直向上，水平峰值位移均呈现不断变大趋势，这是地震波不断向上传播反射作用的特征体现。同时，随基岩处输入地震波强度的增大，水平峰值位移曲线呈现出增大走势，且这种增大走势因坡脚距离不同而趋向各异。

图10柱形图给出了4种分幅距离工况下路基模型A，B，C和D参考点的水平向峰值位移。由图可以看出，在A点，B点和C点3位置处，坡脚距离的逐渐变大，水平峰值位移首先呈变大走势，在10 m坡脚距离处参考点水平峰值位移出现极大值，而后随坡脚距离变大，水平峰值位移逐渐减小。由于地层埋深5.9 m距离地震波的输入位置较近，坡脚距离变化对埋深较深地层的水平峰值位移影响较小。

(a) 坡脚距离5m；(b) 坡脚距离10m；(c) 坡脚距离15m；(d) 坡脚距离20m

3 结论

1) 随着输入地震波强度的增加，模型参考点加速度放大系数表现出减小走势。坡脚距离10 m处，施加63%地震波加速度时程，路基表面与天然地表的加速度放大效应较小；而施加10%，2%地震波，此两参考点的加速度放大效应均呈较大。

2) 施加地震荷载，路基Mises 应力平均值在路基表面处较大，其次是天然地表，在坡脚处较小。坡脚距离的增加对路基表面的Mises 应力平均值变化幅度影响较大，而对天然地表和坡脚变化幅度影响微小。路基S12绝对变化量平均值在天然地表处较大，坡脚处值接近天然地表，在路基表面值较小。坡脚距离的增加对天然地表和坡脚的剪应力S12绝对变化量平均值影响较大，但对路基表面的影响微小。

3) 路基表面和天然地表的水平峰值位移随着坡脚距离的增加，呈现出先上升后下降的变化趋势，在坡脚距离是10 m处参考点水平峰值位移出现极大值。

4) 青藏冻土工程走廊地域辽阔，不同场地冻土层性质变化较大。仅讨论施加北麓河地区地震加速度时程，分幅距离变化对路基的加速度放大效应、应力响应、位移响应的影响，是否具有普适性还需结合更多的现场钻孔资料，并收集实际记录数据进一步验证。后期条件允许情况下开展室内振动台试验以及地震作用下路基现场试验对数值模拟结果验证具有重要意义，以期对高原冻土路基抗震进行更为深入地研究和分析。

(a)路基表面A点；(b)天然地表 B点；(c)地基深2 m C点；(d)地基深5.9 m D点

[1] JIN Huijun, ZHAO Lin, WANG Shaoling, et al. Thermal regimes and degradation modes of permafrost along the Qinghai-Tibet highway[J]. Science in China Series D, 2006, 49(11): 1170-1183.

[2] 李双洋, 张淑娟, 赵德安, 等. 冻土路基动力分析模型及青藏铁路地震灾害评估[J]. 岩土力学, 2010, 31(7): 2179-2187, 2201. LI Shuangyang, ZHANG Shujuan, ZHAO Dean, et al. Dynamical analysis model for frozen embankment and seismic hazard assessment of Qinghai-Tibet railway[J]. Rock and Soil Mechanics, 2010, 31(7): 2179-2187, 2201.

[3] 马巍, 牛富俊, 穆彦虎. 青藏高原重大冻土工程的基础研究[J]. 地球科学进展, 2012, 27(11): 1185-1191. MA Wei, NIU Fujun, MU Yanhu. Basic research on the major permafrost projects in the Qinghai-Tibet plateau[J]. Advances in Earth Science, 2012, 27(11): 1185-1191.

[4] YU Qihao, FAN Kai, YOU Yanhui, et al. Comparative analysis of temperature variation characteristics of permafrost roadbeds with different widths[J]. Cold Regions Science and Technology, 2015, 117: 12-18.

[5] YU Wenbing, XIN Yi, NIU Yongzhi, et al. Dynamic Thermal regime of permafrost beneath embankment of Qinghai-Tibet highway under the scenarios of changing structure and climate warming[J]. Cold Regions Science and Technology, 2016, 126: 76-81.

[6] 杨凯飞, 穆彦虎, 马巍, 等. 气候变暖下青藏高原冻土路基地温场演化规律研究[J]. 地震工程学报, 2018, 40(4): 734-744. YANG Kaifei, MU Yanhu, MA Wei, et al. The evolution law of ground temperature field in permafrost roadbed of the Qinghai-Tibet plateau under climate warming[J]. China Earthquake Engineering Journal, 2018, 40(4): 734-744.

[7] 王英才. 青藏高原高速公路宽幅路基温度场有限元分析[D]. 北京: 北京交通大学, 2013. WANG Yingcai. Finite element analysis on temperature field of large-width highway subgrade in Qinghai-Tibet plateau[D]. Beijing: Beijing Jiaotong University, 2013.

[8] 马巍, 周国庆, 牛富俊, 等. 青藏高原重大冻土工程的基础研究进展与展望[J].中国基础科学, 2016, 6(6): 9-19. MA Wei, ZHOU Guoqing, NIU Fujun, et al. Progress and prospect of the basic research on the major permafrost projects in the Qinghai-Tibet plateau[J]. China Basic Science, 2016, 6(6): 9-19.

[9] LIU Weibo, YU Wenbing, YI Xin, et al. Thermal regime of frozen soil foundation affected by concrete base of transmission line tower on the Tibetan Plateau[J]. Applied Thermal Engineering, 2015, 75: 950-957.

[10] LAI Yuanming, WANG Qiusheng, NIU Fujun, et al. Three-dimensional nonlinear analysis for temperature characteristic of ventilated embankment in cold permafrost regions[J]. Cold Regions Science and Technology, 2004, 38(2/3): 165-184.

[11] 汤涛, 马涛, 黄晓明, 等. 青藏高速公路宽幅路基温度场模拟分析[J]. 东南大学学报(自然科学版), 2015, 45(4): 799-804. TANG Tao, MA Tao, HUANG Xiaoming, et al. Simulation analysis of temperature field of wide subgrade of Qinghai-Tibet highway[J]. Journal of Southeast University (Natural Science Edition), 2015, 45(4): 799- 804.

[12] 汤涛, 马涛, 黄晓明, 等. 青藏高速公路路基降温措施有效性模拟分析[J]. 湖南大学学报(自然科学版), 2016, 43(11): 95-102. TANG Tao, MA Tao, HUANG Xiaoming, et al. Simulation analysis on cooling effectiveness of engineer measures for subgrade of Qinghai-Tibet expressway[J]. Journal of Hunan University (Natural Sciences), 2016, 43(11): 95-102.

[13] 马巍, 穆彦虎, 谢胜波, 等. 青藏高速公路修筑对冻土工程走廊的热力影响及环境效应[J]. 地球科学进展, 2017, 32(5): 459-464. MA Wei, MU Yanhu, XIE Shengbo, et al. Thermal- mechanical influences and environmental effects of expressway construction on the Qinghai-Tibet permafrost engineering corridor[J]. Advances in Earth Science, 2017, 32(5): 459-464.

[14] 董连成, 徐禛, 师黎静, 等. 多年冻土区青藏铁路列车荷载作用下路基振动响应研究[J]. 地震工程学报, 2018, 40(6): 1153-1160. DONG Liancheng, XU Zhen, SHI Lijing, et al. Vibration response analysis of embankments in permafrost regions along the Qinghai-Tibet railway subjected to train loads[J]. China Earthquake Engineering Journal, 2018, 40(6): 1153-1160.

[15] LI Suangyang, LAI Yuanming, ZHANG Mingyi, et al. Seismic analysis of embankment of Qinghai–Tibet railway[J]. Cold Regions Science and Technology, 2009, 55: 151-159.

[16] 刘志强, 陆昊. 冻土路基在地震作用下的动力响应[J].冰川冻土, 2011, 33(4): 807-812. LIU Zhiqiang, LU Hao. Dynamic response of embankment in cold regions to earthquake action[J]. Journal of Glaciology and Geocryology, 2011, 33(4): 807-812.

[17] 费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2009. FEI Kang, ZHANG Jianwei. Application of ABAQUS in geotechnical engineering[M]. Beijing: China Water & Power Press, 2009.

[18] 蒲小武, 王兰民, 吴志坚, 等. 兰州丘陵沟壑区挖方黄土高边坡面临的工程地质问题及稳定性分析[J]. 地震工程学报, 2016, 38(5): 787-794. PU Xiaowu, WANG Lanmin, WU Zhijian, et al. Engineering geological problems of loess high excavation slope in loess hilly and gully region of Lanzhou and its stability analysis[J]. China Earthquake Engineering Journal, 2016, 38(5): 787-794.

[19] 赵涛, 吴志坚, 梁庆国, 等. 青藏高速公路路基地震动力响应分析[J]. 铁道科学与工程学报, 2016, 13(12): 2381-2387. ZHAO Tao, WU Zhijian, LIANG Qingguo, et al. Seismic dynamic response analysis of embankment along the Qinghai-Tibet expressway[J]. Journal of Railway Science and Engineering, 2016, 13(12): 2381-2387.

Influence of distance between two lines on seismic dynamic response of separated embankment along the Qinghai-Tibet Expressway

ZHAO Tao1, 2, LIANG Qingguo1, WANG Yuhong2, CHEN Tuo3, WANG Yan4

(1. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. Shanxi Railway Institute, Weinan 714000, China; 3. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Xuzhou 221116, China;4. School of Civil Engineering, Qinghai University, Xining 810016, China)

In order to study the dynamic response characteristics of separated embankment under seismic wave, combining with field borehole data, taking separated embankment with standard section as the research object, the two-dimensional non-linear dynamic finite element non-correlative flow method was used to establish the separated embankment model with the spacing of 5, 10, 15 and 20 m respectively between left and right slope toe. The effect of change of distance between two lines on the seismic dynamic response of embankment was obtained by applying seismic waves with the exceeding probability of 2%, 10% and 63% in 50 years. The results show that the Mises stress value of embankment surface is greatly affected by the change of slope toe distance, and that the influence on natural surface and slope toe is small. While these effect laws are exactly opposite to shear stress S12value. With the increase of slope toe distance, horizontal peak displacements of separated embankment surface and natural surface show the law of first increasing and then decreasing, meanwhile peak displacement of reference point reach maximum value when slope toe distance is equal to 10 m. This study result is expected to provide reference for type selection and a seismic design of separated embankment in QTEC.

Qinghai-Tibet Engineering Corridor (QTEC); separated embankment; distance between two lines; seismic wave; dynamic response

10.19713/j.cnki.43-1423/u.T20190146

TU445

A

1672 - 7029(2020)01- 0048 - 09

2019-03-04

国家自然科学基金资助项目(41562013)；陕西铁路工程职业技术学院科研基金项目(Ky2017-040)

梁庆国(1976-)，男，甘肃临洮人，教授，博士，从事岩土与地下工程方面的教学与研究；E-mail：lqg_39@163.com

(编辑 涂鹏)