输流直、弯组合管的流体诱发振动分析

摘要： 基于“以直代曲”的思路，提出在输流直管的流固耦合振动微分方程中直接引入稳态组合张力来描述直、弯组合管的横向运动。以固定‑弹性支承式组合管为例，利用基于Laplace变换的新传递矩阵法推导了求解系统固有频率的特征方程，研究了系统的固有频率及临界流速等振动特性，过程中着重考察了稳态组合张力、流动模型修正因子、系统组成等因素对振动特性的影响。提出了“伪模态耦合发散”的概念，发现对于稳态组合张力，不同的取值方式会得到不同的临界流速；系统组成的变化会导致系统的稳定性呈现较大的差异。利用“以曲代直”的思路建立了组合管的振动微分方程，经验证，上述两种思路的计算结果一致。

关键词： 流固耦合振动； 输流直、弯组合管； 固有频率； 稳态组合张力； 临界流速

中图分类号： O327； TH137.7""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0039-08

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.005

Flow-induced vibration analysis of combined straight-curved pipe conveying fluid

LIU Wei¹， WAN Zhiyong²， ZHAO Qianli¹

（1.School of Mechanical Engineering， Changzhou Vocational Institute of Mechatronic Technology， Changzhou 213164， China；2.Changzhou Zhixu New Energy Power Technology Co.， Ltd.， Changzhou 213002， China）

Abstract： Based on the approach that ‘replace curved by straight’， the steady combined force is introduced directly into the fluid structure interaction vibration differential equation of straight pipe to describe straight-curved one’s transverse motion. Taking clamped-elastically supported combined pipe as an example， the new transfer matrix based on Laplace transform is used to derive the system’s characteristic equation calculating its natural frequency， and then the vibration characteristics such as natural frequency and critical velocity are studied. During this process， influences of the steady‑state combined tension， flow model modification factor， and system’s components etc. on the vibration characteristics are investigated. According to the above investigation， the ‘fake coupled-mode divergence’ is firstly put forward， it can be concluded that different steady‑state combined combined tension may lead to different critical velocity， change of system’s components may lead to distinguishing judgement for stability. The vibration differential equation is also established based on the approach ‘replacing straight by curved’， results of the above two thoughts are verified to be the same. The above investigation can provide insights for studying vibration characteristics of other types of pipes and behaviors of other fluid structure interaction mechanics as well， and be of high guiding meanings for theory and values for practice.

Keywords： fluid structure interaction vibration；combined straight-curved pipe conveying fluid；natural frequency；steady-state combined tension；critical velocity

输流管路作为大部分机械设备不可或缺的组成部分，其振动特性也越来越受到广泛的关注。近些年来，人们从实际应用和理论研究的角度对管路系统开展了诸多工作并取得了许多重要的成果^［1⁃6］。正如PAIDOUSSIS^［7］强调的那样：输流管路的流固耦合振动行为已发展成为一种典型的动力学范例，研究其动力学行为不仅能揭示其本身的运动规律，更能将研究经验推广至其他类似的问题中去。

目前，被广泛应用于求解输流管路振动特性的方法主要包括：有限单元法（finite element method，FEM）、微分求积法（differential quadrature method，DQM）、微分变换法（differential transform method，DTM）、传递矩阵法（transfer matrix method，TMM）、伽辽金法（Galerkin method）以及格林函数法（Green function method，GFM）。学者们利用上述方法针对具有不同支承形式、空间构型以及截面形状特点的输流管路进行了稳定性、分岔与混沌行为、强迫振动的位移响应等方面的研究，其中具有代表性的成果主要包括：MISRA等^［8⁃9］利用FEM研究了输流弯管的流体诱发振动特性，并在此基础上结合实验结果提出了关于弯管中心线是否可伸长的三个模型，分别为：不可伸长理论、修正的不可伸长理论和可伸长理论，后续的大多数关于输流弯管的研究^{［10⁃14］}也都是基于上述三个理论而展开的。WANG等分别利用DQM^［15］及其广义形式^［16］对四种典型支承形式输流弯管的动力学行为进行了研究。NI等^［17］利用DTM求解了四类典型支承形式输流直管的动力学特性，并且通过计算得到了各类支承形式下输流直管发生失稳的临界流速。KOO等^［18］利用波动分析法中的动刚度法针对管路的任一单元建立动态刚度矩阵，而后各单元之间通过连续性条件建立传递矩阵，最终扩展至整个管路系统，定义了比较传统的用于求解输流管路振动特性的TMM。ZHAO等^［19］基于Laplace变换提出了L‑TMM传递矩阵法，与传统的TMM相比，利用L‑TMM能够推导得到具有更低阶数的特征方程，大大提高计算效率，随后，他们将之用于研究具有弹性支承输流弯管的稳定性问题。金基铎等^［20］利用伽辽金法推导了两端支承式输流直管的临界流速的表达式。LI等^［21］结合Laplace变换和格林函数的定义推导了具有不同支承形式的输流直管强迫振动稳态响应的表达式，该表达式具有完全封闭的特点。

综上，虽然针对输流直管或弯管流固耦合振动特性的研究已取得了长足的进步，但对直、弯组合管动力学行为的相关工作却鲜有报道，而这类管路恰恰又是工程实际中较为常见的一种结构。因此，本文基于“以直代曲”的思路，将稳态组合张力引入直管的流体诱发振动微分方程中，建立了描述直、弯组合管横向运动的微分方程；利用L‑TMM推导了具有弹性支承输流直、弯组合管计算固有频率的特征方程，并研究了稳态组合张力、流动模型修正因子、系统的组成等因素对振动特性的影响。

1 力学及数学模型

1.1 力学模型

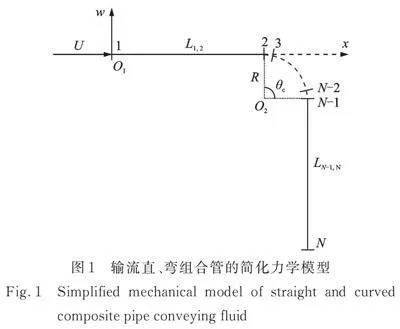
为便于问题的描述，对于由两段直管和一段弯管组合而成的输流管路系统，假设其力学模型可以简化为由两条直线和一条曲线组合而成，对应的力学模型如图1所示，图中省略了两端的支承形式。

基于“以直代曲”的思路，可以考虑将弯管部分划-2个节点，各单元被近似视为直管，那么系统的力学模型则可以转化为如图2所示。在图1和2中，U为横截面内的平均流速，L_{i， j}（i， j1，…，N）表示第i个节点至第j个节点之间管路的长度。

1.2 数学模型

根据文献［7］，输流直管基本形式的无量纲流体诱发振动微分方程为：

（1）

式中，，x表示横坐标，L为直管的总长；，w为横向位移；，t表示时间，E为弹性模量，I为横截面惯性矩，M和m分别表示单位长度的内部流体和管路的质量；，U表示内部流体的平均流速；。

根据MISRA等^［9］的研究结论：当弯管两端均受到支承且忽略重力等因素时，弯管受到的稳态组合张力仅与流体的流动有关，且。但上述结论是以管路内部流体作平推流动为前提的，当考虑其他流动形式时，需要对式（1）中的u²项进行修正，即引入流动模型修正因子^［22］，则根据该组合张力的含义，本文相应地将其修正为。因此，描述与图2对应的输流直管横向运动的微分方程可近似表示为：

（2）

式中，。在这里需要注意的是：当计算直管部分时，取；当计算弯管部分时，取。

当组合管路的一端固定，另一端具有一个线弹簧和扭转弹簧（弹性系数分别用K和K_t表示）时，与式（2）对应的边界条件则可以表示为：

（3）

式中，；。

2 L-TMM推导特征方程

式（2）的解可以表示为：

（4）

式中，i为虚数单位；，表示无量纲特征变量，其中表示特征变量。

将式（4）代入式（2），可得：

（5）

对式（5）的等号两端进行Laplace变换，经过化简可得：

（6）

对式（6）中的分母进行有理化处理，可得：

（7）

将式（7）代入式（6），可得：

（8）

对式（8）的等号两端取Laplace逆变换，结果为：

（9）

式中，

；

；

；。

根据式（9）可以得到和的关系为：

（10）

式中，（i， j1， 2， 3， 4），且

；

。

结合Euler‑Bernoulli梁理论，在任意位置ξ处，管路的位移w、转角θ、转矩M_t和剪力Q可分别表示为：

（11）

（12）

（13）

（14）

综合式（11）～（14），在任意位置ξ处的状态向量可以表示为：

（15）

式中，，且H中的非零项为：

，，，。

根据式（15），可以表示为：

（16）

对于第m个单元，若其两端节点的坐标分别用ξ_m和ξ_m+1表示，则根据式（10），（16）和（15）可知分别有以下表达式，即：

（17）

（18）

（19）

式（17）～（19）中 ξ和q的下标表示节点的编号；T和H的下标表示管路单元的编号。

将式（18）代入式（17），然后将结果代入式（19），经过化简可得：

（20）

式中，，上标l和r分别表示左（left）和右（right）两个方向。

若第m个节点处有弹性支承且弹性系数分别为K（线弹簧）和K_t（扭转弹簧），则根据力的平衡条件，在该节点处有：

， （21）

式中，下标m表示节点的编号。由于任意点处的位移w和转角θ都是连续的，所以不需要标注方向。

根据式（21），可得第m个节点左右两端的状态向量为：

（22）

式中，F的下标表示节点的编号，且（i=1， 2， 3， 4），，，其余元素全部为0。

将式（22）代入式（20），可得：

（23）

于是，对共有N个节点的管路来说，有以下表达式，即：

（24）

令，对于与图2对应的固定‑弹性支承式输流直管，其两端节点处的状态向量分别为：

（25）

（26）

将式（25）和（26）代入式（24），经过整理可得：

（27）

由于式（27）中的M_t1和Q不得为0，所以为了得到非平凡解，系数矩阵的行列式必须为0，即

（28）

由于A为包含无量纲的特征变量以及系统各物理参数的矩阵，因此式（28）为求解具有弹性支承输流直、弯组合管特征值的特征方程。根据上述推导过程可知，通过求解式（28）得到的特征值必然为复数，PAIDOUSSIS^［7］曾经提及，通过求解特征方程得到的特征值，其实部（下文以Re（ω）表示）是系统的固有频率，虚部（下文以Im（ω）表示）与阻尼相关，且稳定性的判据可以描述为：当Re（ω）0，Im（ω）的符号开始改变时对应的流速为发散失稳临界流速（下文以u_cd表示）；当Re（ω）0，Im（ω）的符号开始改变时对应的流速为颤振失稳临界流速（下文以u_cf表示）。

3 正确性验证

3.1 方法的正确性验证

当弹性系数K和K_t取不同值时，管路的支承形式会发生变化，当K或K_t取极限值时会得到典型的支承形式，结果如表1所示。

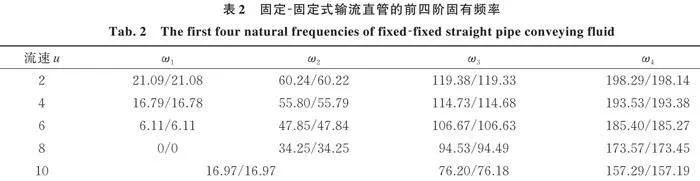
微分变换法（DTM）在计算微分方程方面的正确性已经经过多方验证^{［1⁃3，17］}。当不计稳态组合张力，即时，式（2）可用来描述输流直管的流体诱发振动问题。因此，下面在该前提下同时利用L‑TMM和DTM计算当流动模型修正因子，质量比时固定‑固定式输流直管的前四阶固有频率（计算时以10⁸近似∞），结果如表2所示。

由表2发现，L‑TMM的计算结果与DTM十分相近，证明了方法的正确性。

3.2 模型的正确性验证

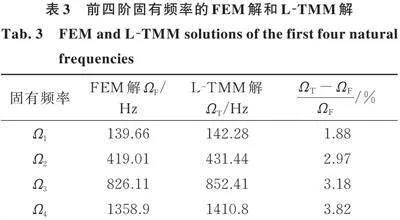
研究一段输流直、弯组合管，其内径r₁12 mm，外径r₂14 mm，两段直管部分的长度均为L"500"mm，弯管部分的中心线半径R100 mm，弯管的张角θ_c90°，材料密度ρ_p7800 kg/m³，弹性模量210 GPa，泊松比μ0.29。内部流体的密度"kg/m³，流速50 m/s，管路两端均为固定支承。

利用L‑TMM对式（2）进行计算，在计算过程中取，N11，同时利用FEM对该管路系统的固有频率进行计算，二者的计算结果如表3所示。

如表3所示，在物理参数和支承形式均一致的情况下，L‑TMM的计算结果均比FEM的大，并且固有频率的阶数越高，引起的偏差越大。但总的来讲，式（2）的有效性得到了验证。

4 参数对振动特性的影响

在本节的研究中，除流速外，假设系统的其他参数与3.2节一致，则质量比β0.262。

4.1 稳态组合张力的影响

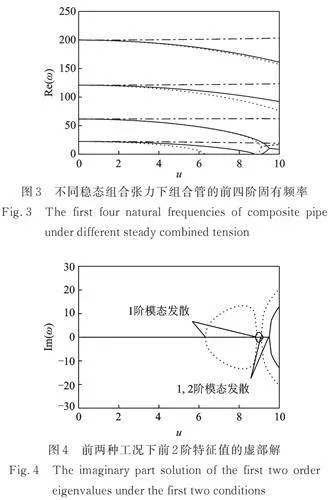
若以平推流模型进行计算，即取流动模型修正因子^［22］。下面研究稳态组合张力沿管路轴线方向取不同值时系统的固有频率与流速的关系，结果如图3所示，计算过程中取。

在图3中，同一种线型由低到高分别表示1～4阶固有频率，且包含以下三种计算工况：

（1） 实线对应仅弯管部分取；

（2） 虚线对应整个管路取；

（3） 点画线对应整个管路取。

对于第3种工况，在计算的流速范围内并不会发生失稳，且仅1阶固有频率随流速降低，其他3阶均增大。对于第1和第2种工况，它们的1，2阶模态发生失稳，其失稳形式如图4所示。

综合图3和4，前两种工况下系统的失稳形式一致，但临界流速却不同。对于第1种工况，其1阶模态发散区间为［8.747， 9.155］，其1，2阶模态耦合颤振临界流速u_cf9.441；对于第2种工况，计算结果则分别为［6.287， 8.988］和u_cf9.048。

4.2 流动模型修正因子的影响

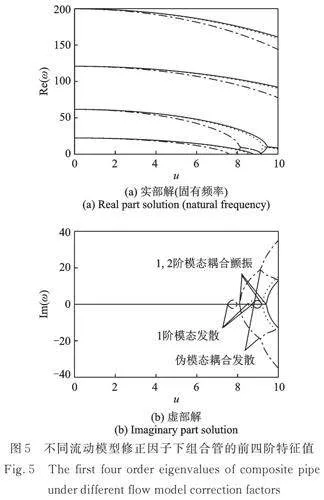
当流体的流动形式不同时，α的取值不同^［22］，具体表现为：当流体做平推流动时，；当流动形式为层流时，；当流动形式为紊流且雷诺数时，（管路内壁光滑）以及（管路内壁粗糙）。下面分别取，4/3和1.040来计算两端固定式输流直、弯组合管的前4阶特征值，结果如图5所示，计算过程中取。

在图5中，实线、虚线和点画线分别对应，1.040和4/3时的计算结果，可以发现随着α的增大，失稳临界流速逐渐减小。在图5（b）中，可以发现当，时出现了不同于已有研究成果的情况，此时固有频率已降为0，阻尼产生了不同趋势的走向，这一点与发散的原理一致，但由于符号未发生改变，导致并未真实地产生发散，因此本文将其命名为“伪模态耦合发散”，以表征模态合二为一后可能产生发散的情况。

4.3 系统组成的影响

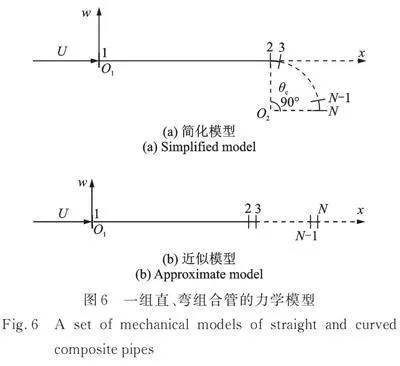
4.1和4.2节是以图2所示的力学模型为基础进行研究的，事实上，当管路系统的组成更为复杂时，结构的振动特性将会发生变化，对于一组包含一段直管和一段弯管的管路系统来说，其简化的力学模型及近似模型如图6所示。

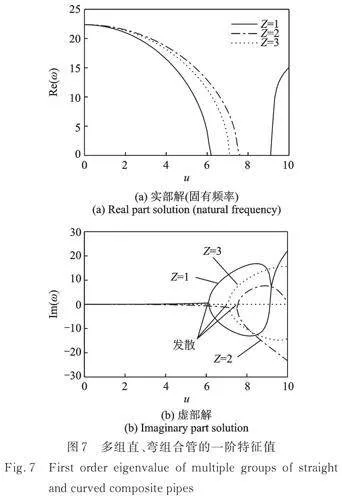
当系统由多组如图6所示的管路组成时，其空间构型将会十分复杂，由于本文所提的数学模型（即式（2））与管路系统具体的空间构型无关，因此具有较高的适用性。下面以如图6所示的一组管路为基础，并以弯管末端连接直管始端为例（即系统中直、弯管交替布置），利用L‑TMM研究多组管路系统的前两阶特征值，结果如图7所示，其中，Z表示组的数量，并且在计算过程中取及。

如图7所示，当系统组成不同时，一阶模态发散失稳的临界流速不同，从理论上来讲，当管路支承端之间的距离越长时系统越容易发生失稳，因此将计算结果换算成有量纲的数据，于是得到由1～3组如图6所示的直、弯组合管路组成的管路系统的临界流速分别为U_cd186.87、115.33和71.79 m/s。

5 “以曲代直”的数学模型

第2～4节全部都是基于“以直代曲”的思路进行的，那么反过来，当弯管中心线的半径足够大时，弯管可被近似视为直管。对于两端支承式输流直、弯组合管，以修正的不可伸长或可伸长理论为基础，得到的关于稳定性的结论更为恰当^［9］，此时，稳态组合张力抵消了微分方程中u²项^［16］，如果不计轴向及横向的附加质量和阻尼，那么以文献［16］的微分方程为基础便得到了该思路下组合管横向的无量纲振动微分方程为：

（29）

式中，，w表示中心线上任一点的切向位移，R为中心线半径；，Θ表示角度坐标，θ_c为弯管的张角；，M和m分别为单位长度流体和管路的质量；，U表示内部流体的平均流速，E为管路的弹性模量，I为横截面惯性矩；，t表示时间；，L表示弯管的弧长。

对于直、弯组合管，在利用L‑TMM对式（29）进行求解时，需要注意：

（1） 计算直管部分时将R取为无穷大（本文以10⁸近似）；

（2） 基于修正的不可伸长理论，法向位移为，其中，表示管路中心线上任一点法向位移r的无量纲形式。

以3.2节的数据为基础，对两种思路下输流直、弯组合管的前四阶固有频率进行计算，结果如表4所示。

由表4可知，由两种思路得到的计算结果几乎一致，再次证明了本文思路及方法的正确性。

6 结" 论

本文基于“以直代曲”的思路，通过在已有的输流直管的流体诱发振动微分方程中引入稳态组合张力建立了描述直、弯组合管横向振动的数学模型，经FEM和L‑TMM对比计算，证明了上述模型的正确性。

随着流动模型修正因子的增加，管路发生失稳的临界流速逐渐减小。上述研究可为研究其他类型管路的振动特性以及其他流固耦合力学行为提供思路。

参考文献：

［1］""""""" CHEN S S， CHEN C K. Application of the differnetial transformation method to the free vibrations of strongly non-linear oscillators［J］. Nonlinear Analysis： Real World Applications， 2009， 10（2）： 881-888.

［2］""""""" YALCIN H S， ARIKOGLU A， OZKOL I. Free vibration analysis of circular plates by differential transformation method［J］. Applied Mathematics and Computation， 2009， 212： 377-386.

［3］""""""" MEI C. Application of differential transformation technique to free vibration analysis of a centrifugally stiffened beam［J］. Computers and Structures， 2008， 86（11-12）： 1280-1284.

［4］""""""" 赵千里， 孙志礼， 柴小冬， 等. 具有弹性支承输流管路的强迫振动分析［J］. 机械工程学报， 2017， 53（12）： 186-191.

ZHAO Qianli， SUN Zhili， CHAI Xiaodong， et al. Forced vibration analysis of fluid-conveying pipe with elastic supports［J］. Chinese Journal of Mechanical Engineering， 2017， 53（12）： 186-191.

［5］""""""" ABDELBAKI A R， PAIDOUSSIS M P， MISRA A K. A nonlinear model for a hanging tubular cantilever simultaneously subjected to internal and confined external axial flows［J］. Journal of Sound and Vibration， 2019， 449： 349-367.

［6］""""""" SAZESH S， SHAMS S. Vibration analysis of cantilever pipe conveying fluid under distributed random excitation［J］. Journal of Fluids and Structures， 2019， 87： 84-101.

［7］""""""" PAIDOUSSIS M P. The canonical problem of the fluid-conveying pipe and radiation of the knowledge gained to other dynamics problems across Applied Mechanics［J］. Journal of Sound and Vibration， 2008， 310（3）： 462-492.

［8］""""""" MISRA A K， PAIDOUSSIS M P， VAN K S. On the dynamics of curved pipes transporting fluid. Part I： inextensible theory［J］. Journal of Fluids and Structures， 1988， 2（3）： 221-244.

［9］""""""" MISRA A K， PAIDOUSSIS M P， VAN K S. On the dynamics of curved pipes transporting fluid. Part II： extensible theory［J］. Journal of Fluids and Structures， 1988， 2（3）： 245-261.

［10］""""" LUO Y Y， TANG M， NI Q， et al. Nonlinear vibration of a loosely supported curved pipe conveying pulsating fluid under principal parametric resonance［J］. Acta Mechanica Solida Sinica， 2016， 29（5）： 468-478.

［11］""""" ZHAO Q L， SUN Z L. In-plane forced vibration of curved pipe conveying fluid by Green function method［J］. Applied Mathematics and Mechanics（English edition）， 2017， 38（10）： 1397-1414.

［12］""""" NI Q， TANG M， WANG Y K， et al. In-plane and out-of-plane dynamics of a curved pipe conveying pulsating fluid［J］. Nonlinear Dynamics， 2014， 75（3）： 603-619.

［13］""" TANG M， NI Q， LUO Y Y， et al. Flow-induced vibration of curved cylinder arrays subject to loose support［J］. Nonlinear Dynamics， 2014， 78（4）： 2533-2545.

［14］""""" NI Q， TANG M， LUO Y Y， et al. Internal-external resonance of a curved pipe conveying fluid resting on a nonlinear elastic foundation［J］. Nonlinear Dynamics， 2014， 76（1）： 867-886.

［15］""""" WANG L， NI Q， HUANG Y Y. Dynamical behaviors of a fluid-conveying curved pipe subjected to motion constraints and harmonic excitation［J］. Journal of Sound and Vibration， 2007， 306（3-5）： 955-967.

［16］""""" WANG L， NI Q. In-plane vibration analyses of curved pipes conveying fluid using the generalized differential quadrature rule［J］. Computers and Structures， 2008， 86（1-2）： 133-139.

［17］""""" NI Q， ZHANG Z L， WANG L. Application of the differential transformation method to vibration analysis of pipes conveying fluid［J］. Applied Mathematics and Computation， 2011， 217（16）： 7028-7038.

［18］""""" KOO G H， YOO B. Dynamic characteristics of KALIMER IHTS hot leg piping system conveying hot liquid sodium［J］. International Journal of Pressure Vessels and Piping， 2000， 77（11）： 679-689.

［19］""""" ZHAO Q L， SUN Z L. Flow-induced vibration of curved pipe conveying fluid by a new transfer matrix method［J］. Engineering Applications of Computational Fluid Mechanics， 2018， 12（1）： 780-790.

［20］""""" 金基铎， 杨晓东， 邹光胜. 两端支承输流管道的稳定性和临界流速分析［J］. 机械工程学报， 2006， 42（11）： 131-136.

JIN Jiduo， YANG Xiaodong， ZOU Guangsheng. Stability and critical flow velocity of supported pipes conveying fluid［J］. Journal of Mechanical Engineering， 2006， 42（11）： 131-136.

［21］""" LI Y D， YANG Y R. Forced vibration of pipe conveying fluid by the Green function method［J］. Archive of Applied Mechanics， 2014， 84（12）： 1811-1823.

［22］""""" GUO C Q， ZHANG C H， PAIDOUSSIS M P. Modification of equation of motion of fluid-conveying pipe for laminar and turbulent flow profiles［J］. Journal of Fluids and Structures， 2010， 26（5）： 793-803.

第一作者："刘" 伟（1977—），男，硕士，高级工程师。E‑mail： lw950626@163.com

通信作者："赵千里（1989—），男，博士，讲师。E-mail： 165187407g@qq.com

基金项目："江苏省第六期“333高层次人才培养工程”资助项目（（2022）3-16-850）；江苏省高等学校基础科学（自然科学）研究面上项目（22KJD130001）；常州市基础研究计划（应用基础研究）项目（CJ20220017）