高速铁路桥梁巨震响应分析

摘要： 为保障高速列车的运行安全，高铁桥梁应具有足够的刚度，这势必会增大结构的地震反应。同时铁路组网，如川藏铁路，已经延伸到西部大震风险区。在高铁桥梁中建立第四级设防的分析方法。在振动台上测试了3个1/5和6个1/8缩尺的圆端矩形截面钢筋混凝土实体桥墩，并进行数值分析。试验结果表明，桥墩在峰值加速度为0.96g（原型0.32g，七度罕遇）以内的地震作用下，墩身仍保持较好的完整性和稳定性，桥墩的地震损伤程度不明显，混凝土桥墩试件没有出现明显的开裂和剥落现象，这表明按规范设计的桥梁具备较好抗震安全性。当地震强度增加到1.71g（原型0.57g，八度罕遇）时，桥墩顺桥向出现中等到严重损伤，而横桥向大多还处于中等损伤。但所有桥墩试件在强度为1.86g的巨震作用下不会发生倒塌破坏。研究表明，在相同地震动作用下，随着纵筋率提高，结构耗能总体呈增加趋势；随着地震设防水平增加，耗能随纵筋率的变化更加显著，试验桥墩可以承担更大的地震荷载。纵筋率对桥墩滞回曲线形状影响较大，增加纵筋率，耗能能力随之增大。需要强调的是，由于高铁桥墩不是按照延性设计，桥墩的体积配箍率均较低，研究表明其对桥墩的滞回性能的影响不明显。

关键词： 抗震性能； 高速铁路桥梁； 圆端矩形实体墩； 巨震； 振动台试验

中图分类号： U442.5⁺5； U443.22""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0191-13

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.021

Giant earthquake response analysis of high‑speed rail bridge based on shaking table tests

Chen Lingkun^1，2， SHI Hongqi¹， Kang Xin³， HU Xiaolun⁴， JIANG Lizhong⁵

（1. Department of Transportation Engineering， Yangzhou University， Yangzhou 225009， China；2. Transportation Science Institute of Nanjing Tech University （Chuzhou） Co.， LTD.， Chuzhou 239050， China；3. Hunan Second Engineering Co.， Ltd.， Changsha 410036， China；4. School of Transportation， Southeast University， Nanjing 211189， China；5.School of Civil Engineering， Central South University， Changsha 410075， China）

Abstract： Railway bridges must have sufficient stiffness to ensure high‑speed train safety， increasing seismic response. The Sichuan‑Tibet Railway network has extended westward. This research analyzes the fourth level of high‑speed railway bridges. Three 1/5 and six 1/8 scaled‑down high‑speed rail （HSR） round‑ended rectangular‑shaped cross‑section solid （RERSCSS） concrete pier were tested and evaluated. The piers survived the earthquake with a peak acceleration 0.96g （prototype 0.32g， seven degrees high‑level earthquake）. Bridge pier specimens showed no concrete cracking or spalling. The code‑designed bridge is seismically safe. When the seismic energy reached 1.71g （prototype 0.57g， eight degrees high‑level earthquake）， the bridge piers showed moderate to severe damage in the cis‑bridge direction. At giant earthquake 1.86g， no bridge abutments collapsed. The study shows that increasing longitudinal reinforcement rate increases structural energy dissipation under the same ground shaking， but increasing seismic protection level increases it more， indicating that test piers can take larger earthquake loads. The bridge pier’s energy dissipation and hysteresis curve depend on the longitudinal reinforcement rate. High‑speed rail piers are not designed for ductility. Therefore， their volume hoop rate and hysteresis performance are low. Based on the analysis， the seismic design classification may be upgraded from the third to forth levels.

Keywords： seismic performance； high‑speed rail bridge； round‑end rectangular solid pier；giant earthquake；shaking table test

高速铁路在全球范围内迅速组网，根据UIC（International Union of Railways）报告，目前正在建设11693 km的高速铁路，这意味着高铁网络将在五到六年内增长近25%^［1］。大量已建和新建的高铁不断延伸到地震断裂带和高地震烈度地区，因此高铁桥梁面临严重的地震威胁^［2］。例如，2010年智利8.8级地震，2016年新西兰8.0级地震，2017年墨西哥海岸近海8.2级地震，以及2018年阿拉斯加湾8.0级地震。特大地震下桥梁损坏问题较为严重^［3‑4］，台湾集集地震震中约20%的桥梁受到不同程度的破坏，严重受损的超过20座。图1为日本地震导致列车脱线出轨^［5］。

国内高铁桥梁的上部结构以箱梁为主，铁路桥墩的断面形式各不相同，主要包括圆端矩形实体桥墩和空心桥墩、矩形实体桥墩和空心桥墩等。高速铁路桥梁桥墩的抗震性能研究引起了许多研究者的关注。相关的桥墩模型拟静力试验、振动台试验及数值模拟工作都值得进行归纳和总结，然后再强调创新。

近年来，研究人员对公路桥梁的钢筋混凝土（RC）实体墩进行了较多的振动台试验研究。LAPLACE等^［6］研究了桥墩在单向地震动下的抗震性能；HACHEM等^［7］对圆柱形桥墩进行了四次模型振动台试验，研究桥墩在双向水平作用下的抗震性能反应。SAKAI等^［8］通过对两个单柱桥墩模型的振动台试验与文献数据相结合，研究了竖向地震激励对桥墩剪切性能的影响。随后，LEE等^［9］根据Caltrans规范对单柱墩脚进行了振动台破坏试验，验证了现有非线性计算模型和规范的合理性。除单柱墩试验外，SCHOETTLER等^［10］和SAIIDI等^［11］进行了基于桥梁系统的振动台试验，研究实时地震下桥梁墩台的抗震性能。这些研究成果为公路RC桥墩的抗震分析理论和设计方法提供了试验依据。

然而，研究高铁RC实体墩的抗震性能及其破坏模式的振动台试验是有限的。XIA等^［12］提出了一种新型铁路屈曲支撑高墩桥并开展振动台试验，如图2（a）所示。结果表明，采用可替换钢屈服支撑后，墩柱在强震下处于弹性状态，新型屈曲支撑具有良好的抗震性能。GUO等^［13］研究了圆端形RC实体墩高速铁路桥的地震灾害机理，如图2（b）所示，提出了高速铁路桥梁的物理与数字材料融合的模拟技术。QI等^［14］开展了三个1/6比例铁路圆端矩形截面RC空心墩的振动台试验，如图2（c）所示，结果发现桥墩都发生了弯曲破坏。这些结果主要是由于可变中空截面特点和高阶振型效应的综合影响，与低周试验中试件的破坏行为有明显不同。

在关于高铁RC实体桥墩抗震性能的研究中，研究者引入了最新的易恢复或者韧性理念进行地震响应分析，并采用试验验证^［15］，但既有的铁路设计规范没有考虑巨震影响，其次，参考基于公路桥梁的研究方法进行铁路桥梁的抗震分析，一般难以完成铁路桥梁的巨震响应评估。试验发现，使用设计加速度进行加载会导致墩底出现微观裂缝，这些裂缝在卸载后会关闭，说明桥墩依然处于弹性受力阶段。当同样水平的位移荷载循环到罕遇地震时，最初的裂缝会增长，桥墩在顺桥向和横桥向均出现轻微至中等程度损伤。总之，由于目前的加载强度，很难评估桥梁结构的损坏情况。要想充分揭示高铁桥梁的地震破坏，需要更显著的加载强度。

出现上述试验现象的宏观解释是：为了满足高速列车的运行安全，高速铁路桥梁应具有足够的刚度，但同时也会增大结构的地震反应。因此，高铁桥墩被设计成大截面和低纵向配筋率，而建筑结构和公路桥则使用轻型、柔性桥墩。低烈度区的高铁桥墩纵向配筋率一般为0.2%，而高地震烈度区的纵向配筋率则在0.5%～1.0%之间^［16］。目前高铁桥墩的震害在集集地震及日本神户地震有过报道^［17］，但是对大震下的高铁桥墩的复盘研究较少。

一般来说，特大地震是指地震烈度等级超过罕遇地震的设计等级。如1966年邢台地震，设计为7度，实际为10度；1975年海城地震，设计为6度，实际为9～11度；1976年唐山地震，设计为6度，实际为11度； 2023年2月6日的土耳其的7.8级的序列地震，其地震动强度超过了9度罕遇的抗震设计最高标准。这些地震造成了巨大的人员伤亡和损失。由于对地震机理和规律的认识还远远不够，目前很难预测巨震事件的发生，所以开展“巨震设防”研究，即在结构破坏非常严重的情况下（特别是低烈度地区），减少人员伤亡，使人员有足够的生存空间，即保证结构不完全倒塌。

对于一般工程结构，目前大多数国家的抗震设计目标是：常遇地震（service⁃level evaluation， SLE）不破坏，设计地震（design earthquake， DE）可修复，罕遇地震（maximum considered earthquake， MCE）不倒塌。最近，越来越多的研究者认识到“巨震”的灾害后果。有研究者对采用最大考虑地震抗震设计的结构地震安全性，仍有相当的怀疑^［18］。原因是采用MCE水平进行抗震设计时，结构倒塌概率不能保证低于10%。也就是说，即使采用MCE进行地震设计，也很难保证建筑物倒塌的风险水平是一致的。随后，美国IBC 2018规范将MCE曲线图与易损性曲线相结合，产生了风险目标MCE_R（risk‑targeted maximum considered earthquake）作为新的地震设计标准^［19］。在美国的大部分城市，结构工程师使用IBC来设计新建筑。然而，到目前为止，还没有MCE_R对铁路桥影响的研究。

需要说明的是，新颁布的第五代地震动参数区划图已提出第四级设防水准“极罕遇地震”（或“巨震”），但是现行抗震设计规范仍然采用三水准设防原则，抗震设计从当前的三水准设防原则向四水准设防原则转变已成为当前工程界迫切需要解决的问题。目前各国对巨震的定义还比较混乱，本文用“巨震”表述来代替“大地震”“特大地震”和“极罕见地震”的定义。其次，抗震设防等级所涉及的关键指标：（1）目标倒塌危险系数；（2）不同设防等级下的目标倒塌概率，在不同规范中是不一样的。在本文中，使用峰值地面加速度（PGA）指标，这与MCE_R的风险等级一致。

因此，对于圆端矩形截面钢筋混凝土实体桥墩，有必要进行专门的针对性的试验和数值研究。本研究制作了3个1/5比例和6个1/8比例的桥墩试件，并在振动台上进行测试。试验过程中，试验系统记录了0.45g、0.60g和0.96g的PGA尺度下的加速度和位移时程曲线，对应7度区和8度区的设计地震和罕遇地震的灾害水平。此外，利用经过验证的OpenSees有限元模型进行参数分析，研究试件在巨震水平（1.05g～1.95g）下的地震行为和破坏程度。本文的工作可以从了解圆端矩形截面钢筋混凝土实体桥墩的地震性能中获益，并为其地震安全评估提供建议。

1 巨震设防等级

目前学术界对巨震没有明确的定义，许多研究规范没有考虑“特大地震”^［20］或“大地震”^［21］，或“超大型地震”^［22］对结构的影响。更重要的是，“特大地震”的定义在不同的规范之间有很大的不同。如FEMA 273^［23］和SEAOC Vision 2000^［24］，也是美国的地震性能设计指南，将特大地震的50年超越概率分别定义为2%和5%，而中国的地震动参数区划图将该指标定义为0.5%（50年超越概率为10^-4，重现期为4975年）^［25］。

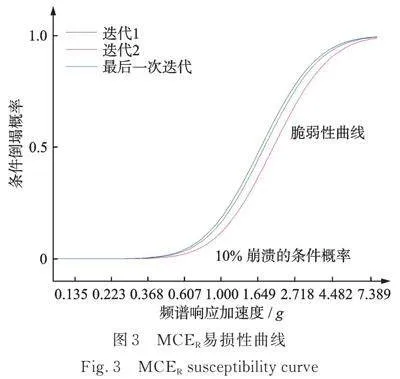
此外，虽然最新的2015版美国NEHRP地震设计规范（FEMA P1050）^［26］是在ASCE/SEI7‑10和国家地震危险区划图NSHM‑2014版^［27］的基础上进一步修订了风险导向的MCE_R区划图，但目前国家规范对“巨震”作用下的条件倒塌概率的可接受水平并没有明确规定。图3为条件倒塌概率为10%的根据2010 ASCE 7标准第21.2.1.2节“方法2”计算的MCE_R易损性曲线^［22］。

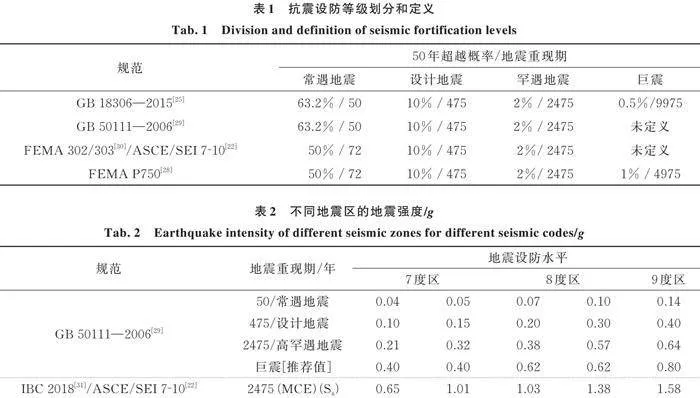
表1给出了不同抗震规范对抗震设防水平的分类和定义。FEMA P750^［28］对“特大地震”的50年超限可能性进行了定义：50年重现期为1%。根据中国地震动参数区划图（GB 18306—2015）^［25］，地震区的地震强度为“特大地震”设计基准地震加速度的2.7～3.2倍。表2给出了不同地震规范下的不同地震区的地震强度。地震动的选择应让用于测试的地面运动组合的水平加速度分量的几何平均谱与《铁路工程抗震设计规范》（GB 50111—2006）^［29］在感兴趣的周期范围内的反应谱相匹配（本研究中测试模型的基本周期为0.049～0.28 s）。

需要注意的是，由于现有规范没有给出各级设防水平的特大地震的地震动强度，本文根据风险导向原则，考虑到巨震的设防水平，给出了一致的风险导向定义。在此基础上，针对现场环境和工程结构的地震易损性水平，给出了风险导向一致的巨震地震动设置水平的建议值。本文给出的建议值见表2。

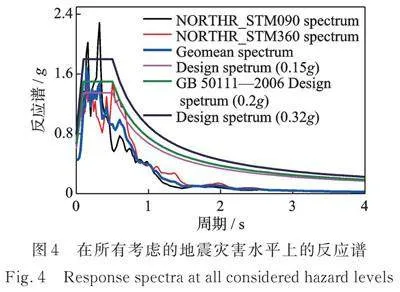
图3中列出了上面的研究所有地震灾害水平的相应5%阻尼加速度响应谱。振动台使用的测试动量是Northridge‑01 1994 Santa Monica City Hall的地面站记录^［30］。所有的地震运动都是通过将加速度值的振幅乘以相应的标量，按危险等级进行缩放的，即7度、8度设计地震事件，被归一化为0.45g和0.60g；7度罕遇地震事件被归一化为0.96g；而MCE_R被归一化为1.86g。所有危险等级的相应响应谱如图4所示。

2 振动台试验

2.1 试验设备及配重

试验在中南大学重载铁路工程结构教育部重点实验室进行。振动台阵列包括A台（固定台）及B，C台（移动台），尺寸均为4 m×4 m（长×宽），最大试件质量30 t，满载下台面最大位移和最大加速度分别为250 mm及1.0g（水平向）、1.6g（竖向）。

以高速铁路32 m简支梁为例，桥梁上部结构梁重、恒载和活荷载共计约1000 t，原型墩高为16 m的缩尺模型仅仅梁体配重就达到近4 t。由于配重较大，本试验使用铅块模拟人工质量。配重箱设计尺寸为3 m×3 m×0.3 m（长×宽×高）。采用20 mm厚的钢板焊接拼装，配重箱内部设置四道横隔板，将配重箱分隔成几个区域，分别在每个区域内放置铅块（铅块尺寸为16 cm×11 cm×5 cm，每块质量约为10 kg，根据配重箱尺寸每层可布置442块铅块）。以2.0 m高模型为例，配重质量为5.47 t。

为防止在振动台试验过程中发生危险^［32］，在振动台台面两侧各布置一个钢管脚手架，同时在配重箱顶部用四根钢丝绳与行车吊钩连接，防止桥墩试件在试验过程中倒塌。

2.2 试验原型

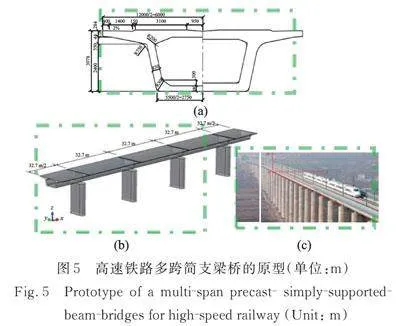
本研究选择跨度为32 m的均匀预制简支梁桥作为原型^［33］。高铁最常见的桥型是简支梁桥，上部结构采用预应力箱梁，跨度为32和24 m。根据中国最繁忙高铁统计，采用预制简支梁桥的线路长度占比，京津铁路为92.08%，京沪铁路为68.24%，哈尔滨至大连铁路为92.58%。

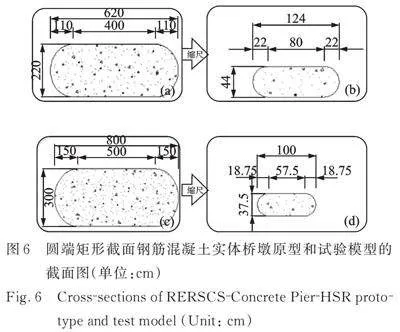
考虑到中国典型高铁的圆端矩形实体桥墩高度的变化范围，本文选择了三种不同高度（8、16、24"m）的桥墩作为试验原型，试验桥墩模型是根据我国高铁桥梁总图制作的^［31］，桥墩模型的抗震要求符合《铁路工程抗震设计规范》（GB 50111—2006）^［29］。原型桥如图5所示；圆端矩形截面钢筋混凝土实体桥墩原型和试验模型的截面如图6所示，其中（a）为8"m高桥墩原型，（b）为8 m高桥墩模型，（c）为16 m和24"m高桥墩原型，（d）为16 m和24 m高桥墩模型。

2.3 模型设计

既有研究表明，轴向荷载比、纵向钢筋比、箍筋与混凝土体积比、长宽比、混凝土强度等对墩柱的抗震性能有明显影响。由于高铁桥墩在自重下的轴向荷载比相对较小，一般在3%左右，因此地震下桥墩的轴向荷载将浮动在自重下的轴向荷载值附近。轴向荷载比设定在15%以内。目前，纵向钢筋比小于1%，箍筋与混凝土的体积比也很小。根据现有的研究，本文确定了每个影响因素的水平，各影响因素的数值如表3所示。本研究采用正交试验法来设计桥墩模型，试验模型的设计参数如表4所示。

在本试验中，墩台模型由C35商品混凝土制成（所有试件的混凝土抗压强度均为35 MPa），墩台模型的纵筋由直径10 mm的热轧HRB335级带肋钢筋制成。箍筋由直径6 mm的热轧HPB235级直圆钢筋制成。根据《铁路工程抗震设计规范》（GB 50111—2006）^［29］，对各类钢筋的抗拉性能进行测试。

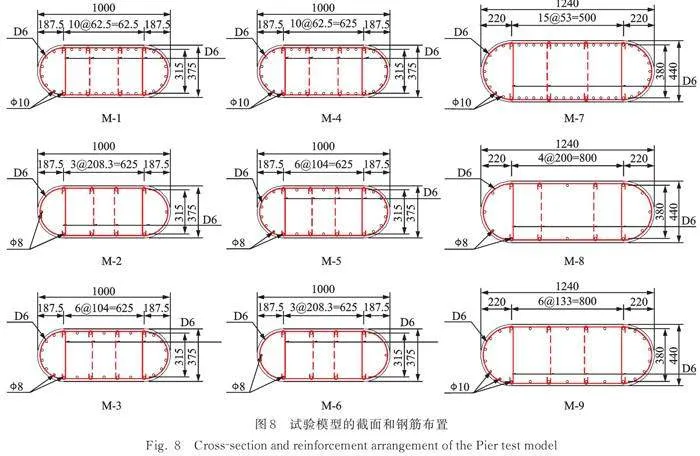
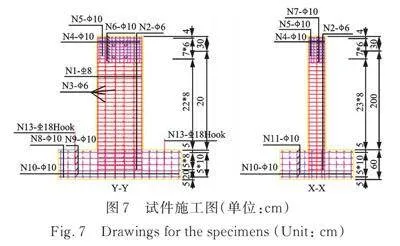
试件施工图如图7所示。由于振动台加载能力（不超过1.0g的PGA尺度）和振动台的尺寸（不超过4 m×4 m）限制，原型墩应采用缩尺模型进行振动台试验。图8为桥墩试验模型的截面和配筋布置。需要注意的是，M‑1～M‑9为试验模型编号；图中尺寸以cm为单位，钢筋直径以mm为单位，图中代表HPB235钢筋，为HRB335钢筋。设计振动台测试方案的关键是确定试样和原型之间的比例关系。

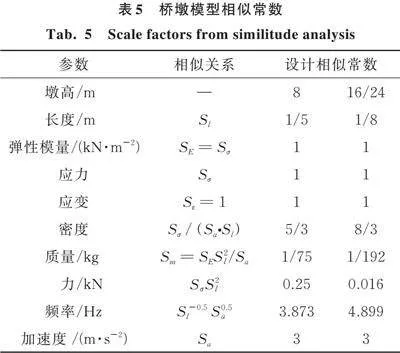
试验根据相似原理来确定桥墩模型主要物理量的相似系数。考虑到模型试件的尺寸越小，其相对强度提高的幅度及试验结果的离散性会越大，且小尺寸的模型试件难以满足构造要求，本试验取墩高8 m的相似比为1∶5，而墩高16、24 m的相似比为1∶8。试验模型与原型主要物理量的相似系数如表5所示。必须使模型材料的参数严格满足相似性比例，这样才能产生可信的试验结果。试验考虑振动台的大小、承载能力和测量设备的放置，选择三个控制因素（S_l、S_σ和S_a）。适当地选择一个缩放规则，以便为桥梁地震性能评估或情景分析提供缩尺桥梁和全尺寸桥梁之间的动态类似性。

2.4 测点布置

所使用的仪器如图所示。在桥墩的底部和顶部沿横向（y‑）和纵向（x‑）设置了四个拉丝位移传感器，以测量桥墩模型的绝对和相对水平位移。为了测试桥墩在地震作用下的加速度变化规律，分别在桥墩的底部和顶部沿横向（y‑）和纵向（x‑）安装加速度传感器。DTx表示x方向位移传感器，DTy表示y方向位移传感器，ATx表示x方向加速度传感器，ATy表示y方向加速度传感器。振动台的加速度响应通过振动台系统的自动反馈直接获得。在测试过程中，MTS AeroPro采集系统采集了应变、位移和加载力的数据。

2.5 地震波选择及加载工况

表6给出了测试方案的细节。在这次测试中，选择了Northridge‑01 1994地震 Santa Monica City Hall波进行振动台测试。之所以选择这个地震记录，是因为该地震波是1994年Northridge地震在洛杉矶盆地西北部产生的一个典型地震记录^［32］，许多建筑物被强烈的地面震动损坏或摧毁。选波过程及不同地震水平对比如图4所示。

根据《铁路工程抗震设计规范》（GB 50111—2006）^［29］，假设场地为V_s30=250～500 m/s的土壤，土壤剖面类型为B型（中硬土），场地特征周期为0.4 s。假设运动的角度为90°分量，以使y方向的桥梁平面内旋转最大化。桥墩试件以高地震区的假定原型为基础，位于地震设防强度为8度的区域，设计地震加速度为0.20g。

值得注意的是，振动台的加速度极限不超过1.00g，本试验选择的最大地震强度为0.96g。根据相似比，具体操作是根据反应谱确定地震灾害等级，然后调整振幅。

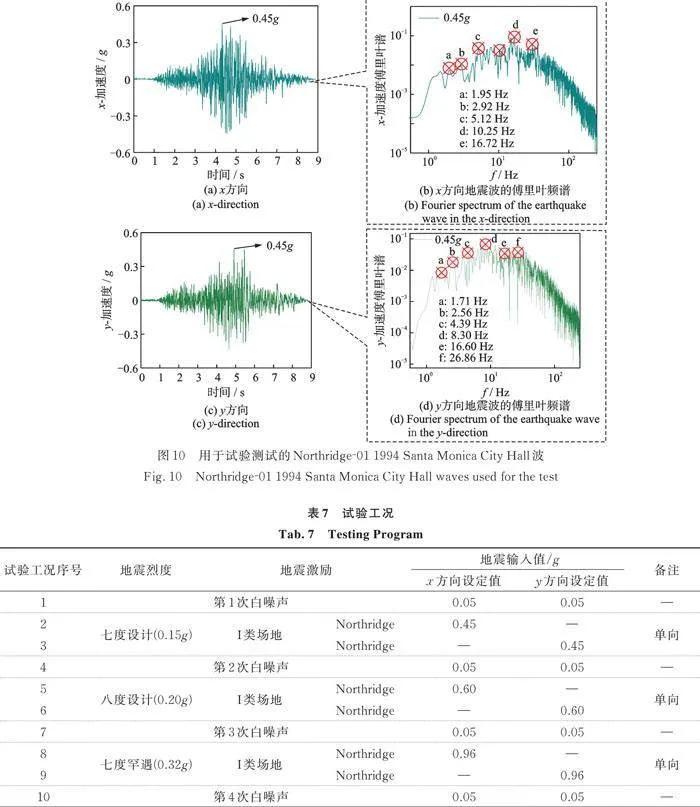
图10（a）和（c）分别是用于试验测试的Northridge‑01 1994 Santa Monica City Hall波（在x和y方向）。如图10（b）和（d）所示，地震波频谱分析表明，x方向的主导频率为10.25 Hz，y方向的主导频率为8.30 Hz。此外，试样还受到了低振幅白噪声激励（PGA尺度为0.05g），监测受到地震激励前后的动态特性变化。

3 试验结果与讨论

高铁桥的抗震性能是由墩顶的加速度和位移来衡量的。因此，它对下部结构的设计有显著影响。墩顶位移一般用于确定在桥上行驶的列车的安全性。在相同的地震烈度下，单向水平地震作用和双向水平地震作用下的墩顶加速度和墩顶位移的最大值相差不大，说明双向水平地震耦合不明显，可以认为是不耦合的^［34］。在单向地震作用下，垂直于水平方向的加速度响应很小，但不为零。

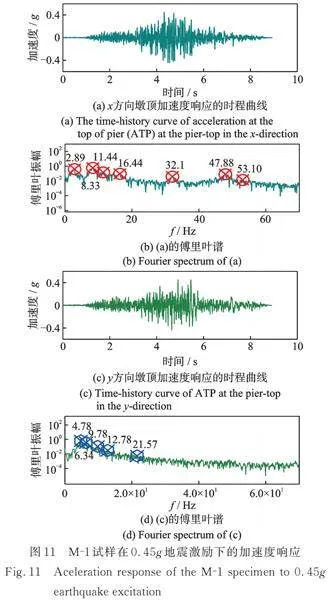
如前所述，试验系统在测试期间记录了不同地震强度（即0.45g、0.60g和0.96g）下的加速度时间历程。例如，图11（a）和（c）显示了加速度时程（在x和y方向），这是从M‑1试样经受0.45g地震激励时得到的。

图11（b）和（d）显示了实践墩部加速度的频谱特征，x方向的主导频率为8.33 Hz，y方向的主导频率为4.78 Hz。在这种情况下，地震反应的傅里叶频谱并不意味着对非线性反应有帮助，除非适当考虑非平稳性。

地震动的非平稳性可以理解为地震动能量在频率和时间上的不均匀分布，而不均匀分布中的能量集中对结构响应很不利，尤其是能量在时间上的集中，在一定程度上对结构非线性响应有较大影响^［33］。

有研究者认为，由于地震动导致的结构损伤，结构的周期一般会变长，如果在强震段以后变得卓越的地震动长周期分量与延长的结构周期相近，结构的反应和破坏将会很大，甚至超过强震段，因为此时结构已经积累了相当的损伤^［34］。这是基于“瞬时共振”的观点，有时的确会发生。不过，这是一个复杂问题的一个方面。尽管地震动的长周期分量通常会在强震段以后变得显著，但是其幅值一般比强震段小得多。因而经常可见的是结构的最大反应发生在强震段，而非地震动的后期。换言之，地震动非平稳性对结构响应的影响应该不仅限于“瞬时共振”，需要进行更深入的研究。基于上述讨论，本研究试图讨论地震动非平稳性对结构非线性响应影响，探索了傅里叶振幅谱的平均周期和希尔伯特谱的瞬时频率‑时程变化系数，以分析结构的地震反应的非稳态频率特征。研究表明，可能是由于试件在y方向的弯曲刚度（EI_y）大于x方向的弯曲刚度（EI_x），该试验模型在y方向上承受更严重的地震作用，即在y方向上有较大的加速度。

根据图4的不同灾害水平的反应谱，对比图8的输入地震的频谱特性分析，本文输入地震可以理解为输入能量相对分散，即所谓“局部时频特性”分布较宽。这可以在斯坦福Jack Baker教授的脉冲地震分类统计研究得到佐证，Northridge‑01 1994 Santa Monica City Hall没有被列入到脉冲型地震类，即Northridge‑01 1994 Santa Monica City Hall属于远场地震波，其输入能量特点为“有效峰值”不足，即地震波中靠近结构基本周期的频率分量对结构影响更大。由于其有效峰值不同于脉冲峰值那样具有长周期，对中小跨径占绝大多数的铁路桥梁的影响更大，这也是本研究选择地震动的因素之一。此外，由于地震力（F=MA）对试件的影响随着地震烈度的增加而增加，因此在x方向和y方向的墩柱试件安装中也可以看到加速度反应的增加趋势。具体来说，墩顶加速度值从0.60g PGA激励下的约0.78g（x方向）和1.25g（y方向）增加到0.96g PGA激励下的1.11g（x方向）和1.65g（y方向）。

对应上述理论分析的试验现象如下：首先，高度为1.6和2.0 m的试件在所有地震工况（试验峰值强度从0.45g到0.96g）结束后没有出现明显的裂缝。其次，对于墩高为1.6和2.0 m的试件，其在遭受实际峰值强度为0.32g（七度罕遇）地震作用时墩底裂缝不明显；而当试件墩高增加到3 m时，桥墩在七度罕遇地震作用下有明显裂缝。第三，所有桥墩桥墩试件在强度为1.92g（原型0.64g，九度罕遇）下不会发生倒塌破坏。

值得注意的是，在图11（b）中，第一个峰值出现在2.89 Hz附近。伴随着地震强度的增加，每个桥墩模型的基本频率都在缓慢下降，这是由于桥墩试件在地震作用下的损坏，导致桥墩的整体刚度下降。对于M‑1试件，在未受地震影响时，x方向的基频约为4.3 Hz。它可能出现在最大地震反应之前的2.89"Hz的小峰值。在y方向，由于其显著的刚度，这种试验现象不会出现。

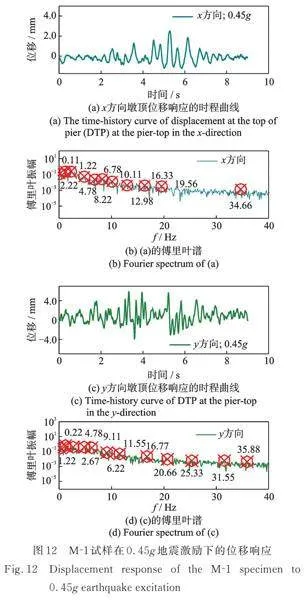
图12（a）和（c）显示了在PGA规模为0.45g的地震下，M‑1试件顶部在x和y方向的位移时程曲线。x方向的主导频率为1.22 Hz，y方向的主导频率为1.44 Hz。应该指出的是，它与加速度响应不相似。x方向的位移响应值（约5.89 mm）比y方向的位移响应值（约2.51 mm）更显著。试验发现，影响桥墩位移的频段比加速度的频度要小，即长周期的地震成分对中小跨径的桥梁影响更大。

试验结果表明，墩顶在x方向的位移比y方向的位移更显著，墩顶的位移随着地震强度和墩身高度的增加而增加。具体地说，位移响应值随着地震强度的增加而增加，从0.60g PGA时的约6.80 mm（x方向）和3.01 mm（y方向）到0.96g PGA时的约7.90 mm（x方向）和3.54 mm（y方向）。

值得注意的是，不同的试验地震强度之间的位移增加几乎是相同的。限于篇幅，其他试验模型的试验结果没有全部列出。试验现象表明，在地震作用下，桥墩高度对桥墩位移响应的影响较为显著，其次是轴压比。相比之下，纵向配筋和箍筋比的影响并不明显。

4 巨震地震响应分析

为了更详细地研究该试件的巨震滞回行为和损伤，利用OpenSees建立了有限元模型，如图13所示，并通过振动台测试的结果进行了验证，分析了建模过程、分析程序和验证情况。

4.1 动力响应分析

对于PGA 1.86g的巨震地震强度，图14（a）显示了试件在地震烈度为1.05g～1.95g时的冲击响应，墩顶加速度与x和y方向的比较。数值结果显示，随着地震强度的增加，墩顶加速度从1.4g增加到2.3g（x方向），2.3g到3.2g（y方向）。

这个结果意味着模型在遭受地震时更容易在x方向受到影响。这个结论的可能原因如下：桥墩截面在横向的弯曲刚度比纵向的弯曲刚度更重要（EI_y gt; EI_x）；桥墩在横向上的基频比纵向上的基频更有效。

此外，为了分析地震烈度对加速度响应的影响，采用试件顶部在x或y方向（即A_x或A_y）记录的最大绝对加速度（墩顶加速度）与PGA（A_g）的比值，表示为R_Ax=A_x/A_g（或R_Ay=A_y/A_g）。图14（b）显示R_Ax和R_Ay随着地震烈度的增加（从1.05g到1.95g）呈下降趋势。

从图14中可以看出，试件在x方向上的地震破坏比y方向上的地震破坏更为广泛。因此，与R_Ay的轻微下降（从1.3g到1.2g）相比，可以发现R_Ax的下降趋势相对明显（从2.2g到1.6g）。这一现象可以合理地解释为该试件的地震破坏是随着地震烈度的增加而形成的，各桥墩在顺桥向及横桥向均出现轻微至中等程度损伤。模型在x和y方向的弯曲刚度都降低了，导致R_Ax和R_Ay的下降趋势。

本节研究了在受到巨震地震作用（PGA从1.05g到1.95g）时，顶部位移响应的比较。从图14（c）可以看出，关于x方向的位移响应D_x比y方向的D_y更显著。具体地说，位移响应在y方向从4.9 mm增加到7.2"mm，在x方向从9.2 mm增加到14.2 mm。数值结果表明，x方向的位移约为y方向的2倍；因此，该试样的抗震保护（如防止梁体脱落）应更加关注x方向的位移响应。

4.2 滞回特性分析

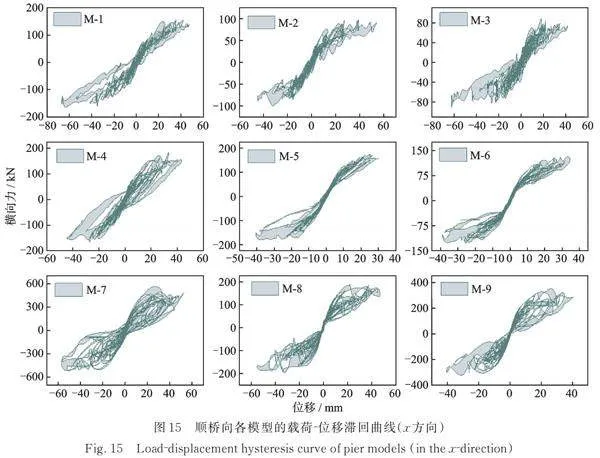
图15给出了巨震1.95g下各桥墩试件的墩顶横向力位移的滞后曲线。桥墩在地震作用下的滞后曲线不规则，反映了地震输入的不规则性和结构地震反应的非线性。类似的滞后曲线可以在文献［17］中看到，试件在特大地震后进入非线性状态，滞后曲线也相对完整。

纵向配筋率对桥墩模型的滞回曲线形状有很大影响。当桥墩模型的纵向配筋率为0.15%时（M‑2，M‑6，M‑8），滞回曲线的捏合特征相当明显，单条滞回环呈S形，面积较小，能量耗散较差。

当纵向配筋率为0.4%时（M‑3，M‑5，M‑9），滞回曲线仍呈捏合状态，卸载曲线与加载曲线的差异开始明显，与纵向配筋率为0.15%时相比，墩身的消能性能略有提高。当纵向配筋率为0.75%时（M‑1，M‑4，M‑7），桥墩模型的滞回曲线变得相对完整，与其他模型相比，消能性能更好。此外，以M‑2，M‑3和M‑1模型为例，其体积箍筋率分别为0.15%，0.30%和0.45%。箍筋量的增加加强了核心混凝土的约束作用，很大程度上提高了空心墩的抗震消能能力。

5 结" 论

本研究对3个1/5和6个1/8比例的圆端矩形截面钢筋混凝土实体桥墩试件进行了一系列振动台试验。建立桥墩有限元模型并进行验证。桥梁地震响应研究的关键问题包括两个方面的内容，第一是地震频谱特性与结构动力特性的动力相互作用，第二是桥梁结构的设计参数对其地震响应的影响。本文重点论述第二点，选择了频率成分含量丰富的地震波，减少地震近场脉冲效应的影响，基于此前提，研究了不同地震强度下桥墩试件的破坏情况，首次考虑了巨震灾害的影响。根据本研究获得的试验和分析结果，得出了以下结论。

（1）典型的圆端矩形截面钢筋混凝土实体桥墩在PGA为0.96g的地震（7度罕遇地震工况）下保持良好的完整性和稳定性，桥墩的地震破坏并不明显。说明按规范设计的圆端空心墩桥梁具有良好的抗震安全性。

（2）考虑到巨震工况输入，当地震烈度增加到1.86g（原型为0.62g）时，沿线桥墩将出现中度和重度破坏，而大部分横桥仍处于轻度破坏状态。在1.95g地震强度之前，所有的桥墩试件都没有观察到倒塌。

（3）纵向配筋率对滞回曲线的形状有明显影响，能量耗散能力随着纵向配筋率的增加而增加。需要强调的是，由于高铁桥墩未按延性设计，桥墩的体积配箍率较低，研究表明其对桥墩滞回性能的影响不明显。

（4）对于确定性的桥梁损伤而言，相比“瞬时共振”效应，“局部时频特性”对桥梁结构影响更大。试验发现，影响桥墩位移的频段比加速度的频段要小，即长周期的地震成分对中小跨径的桥梁影响更大。

参考文献：

［1］""""""" MARC Guigon. The perpetual growth of high‑speed rail development［J］. Global Railway Review， 2020， 26（4）： 52‑54.

［2］""""""" https：//www.eesi.org/papers/view/fact-sheet-high-speed-rail-development-worldwide［EB/OL］.

［3］""""""" NAOI M， SEKO M， SUMITA K. Earthquake risk and housing prices in Japan： evidence before and after massive earthquakes［J］. Regional Science and Urban Economics， 2009， 39（6）： 658‑669.

［4］""""""" THAPA R， RIJAL H B， SHUKUYA M. Field study on acceptable indoor temperature in temporary shelters built in Nepal after massive earthquake 2015［J］. Building and Environment， 2018， 135（1）： 330‑343.

［5］""""""" NAKAMURA Y， SAITA J， SATO T. On an earthquake early warning system（EEW） and its applications［J］. Soil Dynamics and Earthquake Engineering， 2011， 31（2）： 127‑136.

［6］""""""" LAPLACE P， SANDERS D， SAIID M， et al. Shake table testing of flexural dominated reinforced concrete bridge columns：cceer 99‑13［R］. Reno， Nevada： Center for Earthquake Engineering Research， University of Nevada， 1999.

［7］""""""" HACHEM M M， MAHIN S A， MOEHLE J P. Performance of circular reinforced concrete bridge columns under bidirectional earthquake loading［R］. Berkeley， CA： Pacific Earthquake Engineering Research Center， University of California， 2003.

［8］""""""" SAKAI J， UNJOH S. Earthquake simulation test of circular reinforced concrete bridge column under multidirectional seismic excitation［J］. Earthquake Engineering and Engineering Vibration， 2006， 5（1）： 103‑110.

［9］""""""" LEE H， MOSALAM K M. Effect of vertical acceleration on shear strength of reinforced concrete columns［R］. Berkeley， CA： Pacific Earthquake Engineering Research Center， University of California， 2014.

［10］""""" SCHOETTLER M J， RESTREPO J I， GUERRINI G， et al. A full‑scale， single‑column bridge bent tested by shake‑table excitation［R］. Berkeley， CA： Pacific Earthquake Engineering Research Center， University of California， 2015.

［11］""""" SAIIDI M S， VOSOOGHI A， NELSON R B. Shake‑table studies of a four‑span reinforced concrete bridge［J］. Journal of Structural Engineering， 2013， 139（8）： 1352‑1361.

［12］""""" XIA X， ZHANG X， WANG J. Shaking table test of a novel railway bridge pier with replaceable components［J］. Engineering Structures， 2021， 232： 111808.

［13］""""" GUO W， HU Y， GOU H Y， et al. Simplified seismic model of CRTS II ballastless track structure on high‑speed railway bridges in China［J］. Engineering Structures， 2020， 211： 110453.

［14］""""" QI Q， SHAO C， WEI W， et al. Seismic performance of railway rounded rectangular hollow tall piers using the shaking table test［J］. Engineering Structures； 2020， 220： 110968.

［15］""""" JIANG L， KANG X， LI C， et al. Earthquake response of continuous girder bridge for high‑speed railway： a shaking table test study［J］. Engineering Structures， 2019， 180： 249‑263.

［16］""""" HE X， WU T， ZOU Y， et al. Recent developments of high‑speed railway bridges in China［J］. Structure and Infrastructure Engineering， 2017， 13（12）： 1584‑1595.

［17］""""" HASHIMOTO S， FUJINO Y， ABE M. Damage analysis of Hanshin Expressway viaducts during 1995 Kobe earthquake. II： damage mode of single reinforced concrete piers［J］. Journal of Bridge Engineering， 2005， 10（1）： 54‑60.

［18］""""" Building Sesmic Safety Council. NEHRP recommended provisions for seismic regulations for new buildings and other structures［R］. Washington， D.C.： National Institute of Building Science， 1997.

［19］""""" PADALU P K V R， SURANA M. An overview of performance-based seismic design framework for reinforced concrete frame buildings［J］. Iranian Journal of Science and Technology， Transactions of Civil Engineering， 2024， 48（2）： 635-667.

［20］""""" HE X， WU T， ZOU Y， et al. Recent developments of high‑speed railway bridges in China［J］. Structure and Infrastructure Engineering， 2017， 13（12）： 1584‑1595.

［21］""""" STEIN S， GELLER R J， LIU M. Why earthquake hazard maps often fail and what to do about it［J］. Tectonophysics， 2012， 562‑563： 1‑25.

［22］""""" ASCE. Minimum design loads for buildings and other structures［S］. New York： Structural Engineering Institute， 2010.

［23］""""" Building Sesmic Safety Council. NEHRP guidelines for the seismic rehabilitation of buildings［R］. Washington， D.C.： National Institute of Building Science， 1997.

［24］""""" SEAOC. Performance‑based seismic engineering of buildings［R］. Sacramento， CA： Structural Engineers Association of California， 1995.

［25］""""" 中华人民共和国国家质量监督检验检疫总局， 中国国家标准化管理委员会. 中国地震动参数区划图： GB 18306―2015［S］. 北京： 中国标准出版社， 2015.

""""""" General Administration of Quality Supervision， Inspection and Quarantine of the People’s Republic of China， Standardization Administration of the People’s Republic of China. Seismic ground motion parameters zonation map of China： GB 18306—2015［S］. Beijing： Standards Press of China， 2015.

［26］""""" Building Sesmic Safety Council. NEHRP recommended provisions for seismic regulations for new buildings and other structures［R］. Washington， D.C.： National Institute of Building Science， 2015.

［27］""""" REZAEIAN S， PETERSEN M D， MOSCHETTI M P， et al. Implementation of NGA‑West2 ground motion models in the 2014 U.S. National Seismic Hazard Maps［J］. Earthquake Spectra， 2014， 30（3）： 1319‑1333.

［28］""""" Building Seismic Safety Council. NEHRP recommended seismic provisions for new buildings and other structures： FEMA P750［S］. Washington， D. C.： National Institute of Building Science， 2009.

［29］""""" 中华人民共和国建设部，中华人民共和国国家质量监督检验检疫总局. 铁路工程抗震设计规范： GB 50111―2006［S］. 北京： 中国计划出版社， 2009.

Ministry of Construction of the People’s Republic of China， General Administration of Quality Supervision， Inspection and Quarantine of the People’s Republic of China. Code for seismic design of railway engineering： GB 50111—2006［S］. Beijing： China Planning Press， 2009.

［30］""""" Building Seismic Safety Council. NEHRP recommended provisions for seismic regulations for new buildings and other structures： FEMA 302/303［S］. Washington， D.C.： National Institute of Building Science， 1997.

［31］""""" International Code Council. 2018 international building code［S］. Washington D. C.： International Code Council， 2018.

［32］"nbsp;""" GRAVES R W， PITARKA A， SOMERVILLE P G. Ground‑motion amplification in the Santa Monica area： effects of shallow basin‑edge structure［J］. Bulletin of the Seismological Society of America， 1998， 88（5）： 1224‑1242.

［33］""""" 时速350公里高速铁路预制后张法预应力混凝土简支箱梁设计图［R］. 北京：铁道部经济规划院， 2011.

General construction drawing for railway engineering construction， 350 km/h high‑speed railway precast post‑tensioning prestressed concrete simply supported box girder （span 32m， single line）［R］. Beijing： Economic Planning Institute of Ministry of Railways， 2011.

［34］""""" PENZIEN J， WATABE M. Characteristics of 3‑dimensional earthquake ground motions［J］. Earthquake Engineering amp; Structural Dynamics， 1974， 3（4）： 365‑373.

通信作者： 陈令坤（1974—），男，博士，副教授。E‑mail： lingkunchen08@hotmail.com

基金项目："扬州市重点研发计划（社会发展）项目（YZ2023077），国家重点研发计划“交通基础设施”重点专项资助项目（2021YFB2600600，2021YFB2600602）