考虑局部场地效应的深水多跨连续梁桥纵桥向地震响应分析

摘要： 桥梁结构抗震设计时应考虑桥墩处局部场地条件对其地震响应的影响。多点激励反应谱法是进行空间地震动作用下桥梁结构抗震性能分析的常用方法。对于深水桥梁结构，现有的多点激励反应谱法未考虑水体的作用。本文基于辐射波浪理论，在桥梁结构振动方程中引入动水压力，建立考虑流固耦合作用的多点激励反应谱法，并验证其正确性。以某深水5跨连续梁桥为例，通过改变桥墩所处场地类型、抗震设防烈度、设计地震分组等参数，研究了不同场地条件下桥梁的纵向地震响应，揭示了局部场地效应对多跨连续梁桥纵向地震响应的影响规律。结果表明，随着桥墩3场地逐渐变软，其墩顶相对位移最多减小93.0%，场地类型对墩顶相对位移的影响大于对主梁轴力和墩底弯矩的影响；随着抗震设防烈度的增大，桥墩墩顶相对位移、主梁轴力和墩底弯矩增大7倍；随着震中距的增大，桥墩墩顶相对位移最多增大41.0%，主梁轴力增大18.0%左右，墩底弯矩增大30.0%左右。

关键词： 局部场地效应； 深水桥梁； 纵向地震响应； 反应谱法； 多点激励

中图分类号： U441⁺.2""" 文献标志码： A""" 文章编号： 1004-4523（2025）01-0154-08

DOI：10.16385/j.cnki.issn.1004-4523.2025.01.017

Longitudinal seismic response analysis of multi‑span continuous girder bridges considering local site effects

WU Kun¹， MA Jie¹， SU Junsheng²， CHEN Yu¹， HUANG Xin¹， QI Lin¹， LI Changhui¹

（1.School of Transportation Science and Engineering， Civil Aviation University of China， Tianjin 300300， China；2.School of Civil Engineering， Tianjin University， Tianjin 300350， China）

Abstract： In the seismic design of bridge structures， the influence of local site conditions at piers on the seismic response should be considered. The multi‑support response spectrum method is a common method for seismic performance analysis of bridge structures under spatial ground motion. For deep‑water bridge， the existing method cannot include the water‑structure interaction. Based on the radiation wave theory， this paper proposed a multi‑support response spectrum considering the water‑structure interaction by introducing the term of hydrodynamic pressure into the vibration equation of the bridge. The correctness of the method was verified. Taking a typical five‑span continuous girder bridge as an example， the seismic response of the bridge under different site conditions is studied by changing the site type of the pier， seismic intensity， and design seismic group. The influence law of local site effect on the seismic response of the multi‑span continuous girder bridge is revealed. The results show that with the softening of site of pier 3， the relative displacement at top of pier 3 decreases by up to 93.0% at most. The influence of site type on pier displacement is greater than that of the axial force of girder and the bending moment at bottom of pier. With the increase of seismic intensity， the relative displacement at top of pier， axial force of girder and bending moment at bottom of pier increase by 7 times. With the increase of epicenter distance， the relative displacement at top of pier increases by 41.0%， the axial force of girder increases approximately by 18.0%， and the bending moment at bottom of pier increases approximately by 30.0%.

Keywords： local site effect；deep‑water bridge；longitudinal seismic response；response spectrum method；multi‑support excitation

对于大跨桥梁结构，桥墩间距离通常较大，不同桥墩处场地条件往往不同，因此需要考虑地震动空间效应对结构地震响应的影响。地震动空间效应主要包括行波效应、部分相干效应和局部场地效应。其中，行波效应是指由于桥墩间距较大，地震波从震源传播到各桥墩处的时间不同，使得不同桥墩处地震波时程产生差异；部分相干效应是指由于地震波在土层不同介质中的折射、反射和散射及由震源到达各支撑处的叠加方式不同，使得不同桥墩处地震波时程产生差异；局部场地效应是指由于不同桥墩处场地土层分布不同，使得地震波从震源传播到桥墩处地表产生差异。

时程分析法和随机振动法是分析桥梁地震响应的主要方法。研究表明，地震动空间效应对桥梁结构抗震性能的影响不可忽略^［1‑9］。李忠献等^［1］采用时程分析法，基于ABAQUS软件建立4跨连续梁桥模型，分析了行波效应对桥墩墩底应力和墩顶相对位移的影响，结果表明墩底应力最多增大29.9%。王浩等^［2］、闫斌等^［3］采用时程分析法分别研究了行波效应对大跨度中承式钢管混凝土（CFST）拱桥和简支梁桥地震响应的影响。贾少敏等^［4］基于时程分析，采用随机模拟法，研究了多点激励下减震桥梁的位移响应。可以看出，针对行波效应下桥梁结构地震响应的研究较多，而针对深水桥梁局部场地效应的研究较少。

相比时程分析法，随机振动法具有计算效率高、计算结果代表性强等特点。在多点多维激励分析中，多点激励反应谱法是目前常用的一种随机振动方法。多点激励反应谱法（MSRS法）最早由KIUREGHIAN等^［10］提出，采用MSRS法对金门大桥进行多点激励分析^［11］，以验证其正确性。随后，ERNESTO等^［12］利用多自由度系统频率响应函数的性质将MSRS法中动力响应项的四重求和简化成三重求和。KDNAKLI等^［13］通过考虑截断高阶振型的拟静力贡献提出改进的MSRS法，并对新引入的互相关系数进行研究。WANG等^［14］采用力相关Ritz向量代替振型向量表示结构位移，提出基于Ritz向量的MSRS法，大大提高了原MSRS法的计算效率。此外，国内学者王君杰等^［15］、叶继红等^［16］、刘先明等^［17］、李杰等^［18］、刘洪兵等^［19］也对MSRS法进行了推导和简化。需要指出的是，对于深水桥梁，已有MSRS法未考虑水体的作用。

本文基于KIUREGHIAN等提出的MSRS法，采用辐射波浪理论计算桥墩动水压力，建立考虑流固耦合作用的多点激励反应谱法（FSI‑MSRS法），采用MATLAB和OpenSees软件编制计算程序。通过与时程分析法计算结果的对比，验证本文提出的FSI‑MSRS法的正确性。以某5跨连续梁桥为例，研究纵桥向地震作用下局部场地效应对桥梁位移、内力等动力响应的影响规律。

1 考虑流固耦合作用的多点激励反应谱法

多点激励作用下，桥梁结构的振动方程可表示为：

（1）

式中，x=［x₁，…， x_n］^T为上部结构非约束自由度的n维位移列向量；u=［u₁，…，u_m］^T为桥墩支撑处约束自由度的m维位移列向量；M、C和K分别为结构非约束自由度的n×n维质量、阻尼和刚度矩阵；M_g、C_g和K_g分别为桥墩支撑处约束自由度的m×m维质量、阻尼和刚度矩阵；M_c、C_c和K_c分别表示上述两组自由度之间的n×m维耦合质量、阻尼和刚度矩阵；F为墩底约束自由度处的m维反力列向量；P为桥墩受到周围水体的动水压力。

根据辐射波浪理论，地震作用下圆形桥墩单位高度受到的动水压力由刚体振动动水压力和弹性振动动水压力组成^{［20‑22］}：

（2）

（3）

（4）

式中，M^g为刚体振动附加质量；M^t为弹性振动附加质量；为对角矩阵M^g的对角元素；为矩阵M^t的元素；r为桥墩迎水面宽度；ρ为水体密度；h为水深；z_j为第j个节点的z坐标；β_m、λ_n为实数；L_j为第j个积分单元长度；Γ_i为积分区间；、f_m（）为函数。

将结构非约束自由度的位移x分解成拟静力位移x_s和动力位移x_d：

（5）

将式（5）代入式（1），展开第一行，可得拟静力位移：

（6）

式中，为影响矩阵，将式（6）代入式（1），展开第二行，化简后可得：

（7）

对式（7）进行求解，采用结构振型表示动力位移，可得结构任意响应z：

（8）

式中，q为转换向量；a_k为有效影响系数；b_ki为有效振型参与系数；s_ki（t）为结构的第i个振型在支撑加速度作用下的响应。

根据平稳随机振动理论，可得峰值响应PR的均值：

（9）

（10）

（11）

（12）

式中，u_k，max为支撑激励位移时程u_k的峰值；D_k（ω，ξ）为支撑激励的位移反应谱值；为结构振动频率；为支撑k和支撑l处位移的互相关系数；为支撑k处位移和支撑l处加速度时程作用下振型j的响应之间的互相关系数；为支撑k处加速度时程作用下振型i的响应和支撑l处加速度时程作用下振型j的响应之间的互相关系数；σ_x为物理量x的标准差；H_i（）为振型i的频率响应函数；G_xy（）为物理量x与物理量y之间的互功率谱。式（9）等号右边第一项为拟静力响应，第三项为动力响应，第二项为拟静力和动力耦合响应。

上述即为本文提出的考虑流固耦合作用的多点激励反应谱法（FSI‑MSRS法）。由式（7）可以看出，考虑桥墩地震动水压力后，等号两边质量矩阵并不相等，因此无法直接采用有限元法求解式（7），而FSI‑MSRS法可以很好地解决这个问题。

2 桥梁模型

2.1 有限元模型

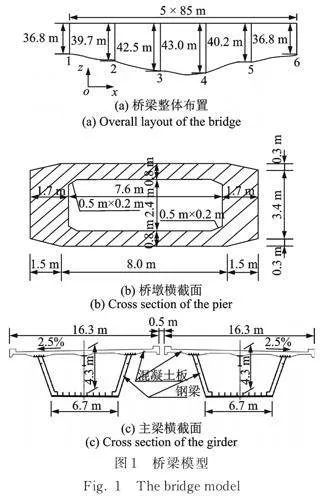
5跨连续梁桥如图1所示，桥梁跨度为5×85 m，桥墩高度为36.8～43.0 m不等，水面距边墩墩底30"m；桥墩采用钢筋混凝土空心矩形截面，主梁采用钢筋混凝土桥面板‑钢箱组合截面。

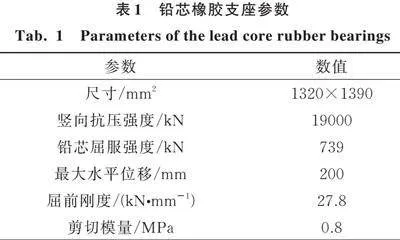
采用OpenSees软件建立桥梁有限元模型时，混凝土采用“Concrete02”本构模型，桥墩截面核心区混凝土采用Mander模型考虑箍筋的约束作用，钢材采用“Steel02”本构模型。由于桥墩为主要受力构件，采用纤维单元进行精细化模拟，桥墩截面纤维网格尺寸约8 cm，长度方向划分150个纤维网格，高度方向划分50个纤维网格；主梁采用elasticBeamColumn单元模拟，每5 m建立一个单元，每个单元设置5个积分点，elasticBeamColumn单元输入的面积、惯性矩等参数根据图1（c）双幅主梁横截面进行计算，计算时将钢箱梁按照弹性模量等效为混凝土梁；每个桥墩与主梁之间设置两个铅芯橡胶支座，采用6个方向的弹簧单元进行模拟，铅芯橡胶支座的参数如表1所示。

为了考虑桥墩周围水体的作用，将式（7）中以附加质量的形式添加到桥墩水下节点。需要说明的是，OpenSees有限元模型仅用于求解系数a_k和b_ki，施加的荷载并非式（7）等号右边含有M^g的荷载。在支撑k处沿地震方向施加单位位移，所求位置的响应即为该响应的a_k值；对结构施加荷载，所求位置的响应即为该响应的b_ki值，其中，为振型参与系数，为第i振型的振型向量。

2.2 输入激励

本文地震动方向为水平方向（x向，纵桥向）。桥墩支撑处输入激励的反应谱采用《建筑抗震设计规范》（GB 50011—2010）^［23］规定的反应谱，分别改变场地类型、场地抗震设防烈度、设计地震分组3个参数，研究不同场地条件对桥梁结构地震响应的影响。其中，抗震设防烈度取6度、7度、8度和9度，设计地震分组取第一组、第二组和第三组，场地类型取Ⅰ₁，Ⅱ，Ⅲ和Ⅳ类。

2.3 结构振动特性

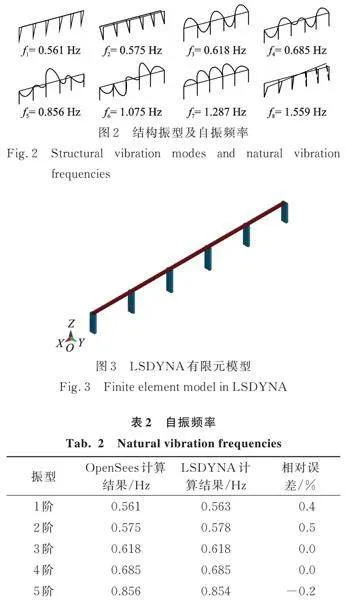
图2给出了5跨连续梁桥的前8阶振型及自振频率。为了验证模型的正确性，采用LSDYNA建立有限元模型，如图3所示，得到前5阶振型和自振频率与图2一致，自振频率计算结果及相对误差如表2所示。因此，本文建立的模型是正确的。

2.4 方法验证

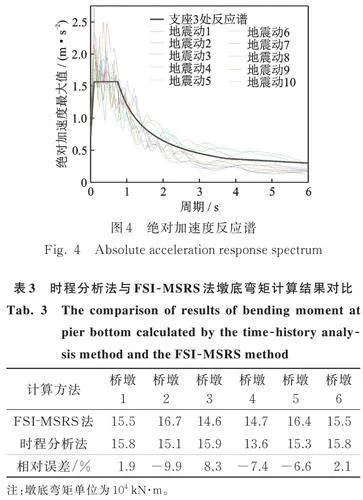
采用文献［24］的方法，生成10组空间地震动，利用OpenSees进行时程分析，计算每组地震动作用下的结构响应，求得其响应峰值的均值，并与本文提出的FSI‑MSRS法计算结果进行对比。图4给出了FSI‑MSRS法采用的支座3处反应谱与时程分析法支座3处10条地震动反应谱的对比。表3对比了采用时程分析法与FSI‑MSRS法的桥墩墩底弯矩计算结果，可以看出，不同桥墩的墩底弯矩误差在10%以内。根据《建筑抗震设计规范》（GB 50011―2010）^［23］，时程分析结果的平均值大于反应谱法的80%即可。因此，上述结果可以验证本文有限元模型和计算方法的正确性。

3 结果分析

3.1 场地类型的影响

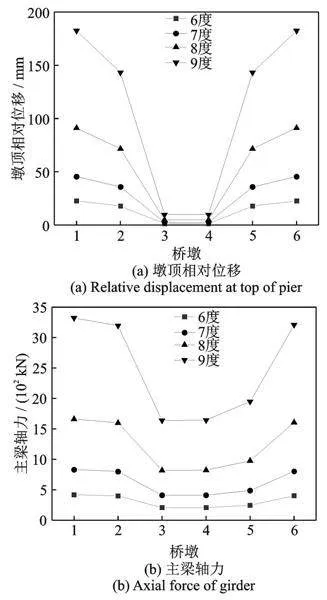
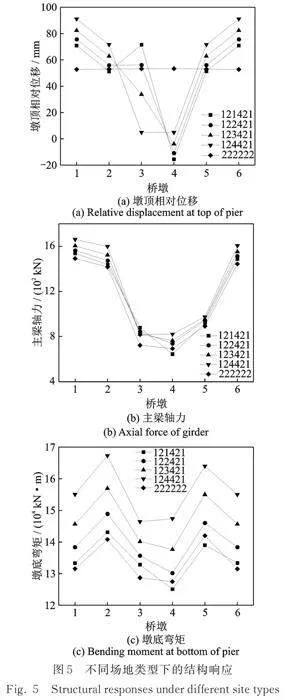
图5给出了纵桥向地震作用下桥墩墩顶相对位移、主梁轴力和墩底弯矩随桥墩3场地类型的变化情况，并与一致激励工况进行对比，其中抗震设防烈度为8度，设计地震分组为第二组。图中1，2，3，4分别代表Ⅰ₁、Ⅱ、Ⅲ、Ⅳ类场地，例如“124421”表示桥墩1～6处的场地类型分别为Ⅰ₁、Ⅱ、Ⅳ、Ⅳ、Ⅱ、Ⅰ₁。图中位移值为负表示桥墩墩顶相对墩底向x轴反向运动。

由图5（a）可知，多点激励下桥墩墩顶相对位移两边大、中间小，这是因为中间桥墩处场地较软，墩底绝对位移大于两边桥墩，所以其墩顶相对位移小于两边桥墩。随着桥墩3场地逐渐变软，桥墩3墩顶相对位移明显减小，其他桥墩墩顶相对位移逐渐增大。桥墩3场地类型从Ⅰ₁到Ⅳ变化，桥墩3相对位移从72 mm减小到5 mm，减小了93.0%；桥墩2相对位移从51 mm增大到72 mm，增大了41.1%。

由图5（b）可知，主梁轴力两边大、中间小，这符合结构力学的受力规律。随着桥墩3场地逐渐变软，桥墩3处主梁轴力略有减小，其他桥墩处主梁轴力有所增大，最多增大27.4%。由图5（c）可知，桥墩墩底弯矩基本呈对称分布，桥墩2和5的墩底弯矩明显大于其他桥墩；随着桥墩3场地逐渐变软，桥墩墩底弯矩逐渐增大，桥墩3墩底弯矩增大10%，其他桥墩墩底弯矩增大16%左右。对比图5（a）和（b）、（c）可知，场地类型对位移的影响明显大于轴力和弯矩，这是因为场地类型对式（9）中拟静力响应的贡献大于动力响应，而位移的大小主要由拟静力响应决定，轴力、弯矩的大小主要由动力响应决定。

对比多点激励和一致激励下的结构响应可知，多点激励增大了不同桥墩墩顶相对位移之间的差距，即增大了桥墩之间的相对位移，一致激励时不同桥墩的墩顶相对位移几乎相同，多点激励时桥墩墩顶相对位移最多相差10倍以上；除个别工况外，多点激励与一致激励下主梁轴力和墩底弯矩变化较小，相差10%左右。因此，大跨桥梁抗震分析时应考虑多点激励的影响，同时说明本文方法的提出是必要的。

改变桥墩1或桥墩2处场地类型，计算结果与图5类似，这里不再列出。

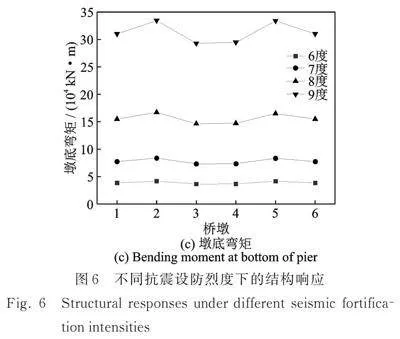
3.2 场地抗震设防烈度的影响

图6给出了纵桥向地震作用下桥墩墩顶相对位移、主梁轴力和墩底弯矩随抗震设防烈度的变化情况，其中各桥墩处场地类型分别为Ⅰ₁、Ⅱ、Ⅳ、Ⅳ、Ⅱ、Ⅰ₁，设计地震分组为第二组。由图6（a）可知，桥墩墩顶相对位移基本呈对称分布，随着抗震设防烈度的增大，墩顶相对位移逐渐增大，这是因为随着抗震设防烈度的增大，地震动强度不断增大。此外，中间桥墩墩顶相对位移增大的幅度较大，即抗震设防烈度越大，差动效应越明显。抗震设防烈度从6度增大到9度，各桥墩墩顶相对位移增大7倍，桥墩1的墩顶相对位移从23 mm增大到182 mm。由图6（b）和（c）可知，随着抗震设防烈度的增大，主梁轴力和墩底弯矩逐渐增大，不同位置处主梁轴力和桥墩墩底弯矩增大7倍。对比图5和6可知，与场地类型相比，抗震设防烈度对桥梁地震响应的影响更大，这是因为抗震设防烈度直接决定加速度反应谱的峰值。

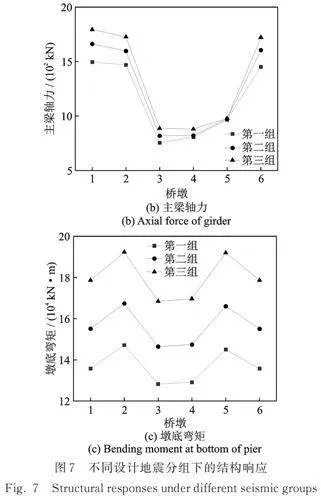
3.3 设计地震分组的影响

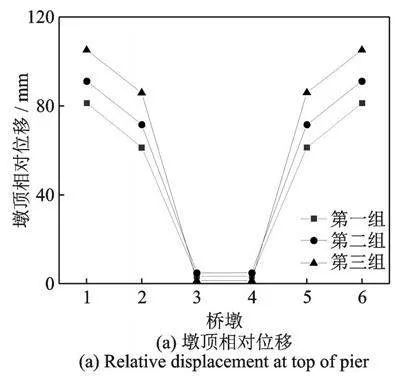
图7给出了纵桥向地震作用下桥墩墩顶相对位移、主梁轴力和墩底弯矩随设计地震分组的变化情况，其中各桥墩处场地类型分别为Ⅰ₁、Ⅱ、Ⅳ、Ⅳ、Ⅱ、Ⅰ₁，设防烈度为8度。根据《建筑抗震设计规范》（GB 50011—2010）^［23］，设计地震分组第一、二、三组分别表示近震、中震、远震，即设计地震分组越大，震中距越远。由图7（a）可知，随着震中距的增大，桥墩墩顶相对位移逐渐增大，桥墩3和4的相对位移绝对值较小，可以忽略；随着设计地震分组从第一组到第三组变化，桥墩1和6的相对位移从81 mm增大到105"mm，增大了29.6%；桥墩2和5的相对位移从61 mm增大到86 mm，增大了41.0%。由图7（b）可知，随着震中距的增大，桥墩4和5的主梁轴力变化较小，其他位置主梁轴力增大18.0%左右。由图7（c）可知，随着震中距的增大，各桥墩墩底弯矩增大30.0%左右。

4 结" 论

（1）场地类型对位移的影响大于轴力和弯矩，随着桥墩3场地逐渐变软，桥墩墩顶相对位移最多减小93.0%，最多增大41.1%，主梁轴力、墩底弯矩最多增大27.4%；原因是场地类型对拟静力响应的贡献大于动力响应，而位移的大小主要由拟静力响应决定，轴力、弯矩的大小主要由动力响应决定。

（2）随着抗震设防烈度的增大，桥墩墩顶相对位移、主梁轴力、墩底弯矩逐渐增大；抗震设防烈度从6度增大到9度，桥墩墩顶相对位移、主梁轴力、墩底弯矩均增大7倍。

（3）随着震中距的增大，桥墩墩顶相对位移、主梁轴力、墩底弯矩逐渐增大；桥墩墩顶相对位移最多增大41.0%，主梁轴力增大18.0%左右，墩底弯矩增大30.0%左右。

需要说明的是，本文提出的方法属于反应谱方法，目前只能进行结构线性响应分析，可以结合已有非线性反应谱或等效线性反应谱方法考虑结构的非线性效应。

参考文献：

［1］""""""" 李忠献， 黄信. 行波效应对深水连续刚构桥地震响应的影响［J］. 工程力学， 2013， 30（3）： 120‑125.

LI Zhongxian， HUANG Xin. Influence of traveling wave effect on seismic responses of continuous rigid-framed bridge in deep water［J］. Engineering Mechanics， 2013， 30（3）： 120‑125.

［2］""nbsp;"""" 王浩， 李峰峰， 宗周红， 等. 大跨度CFST拱桥地震行波效应研究［J］. 振动工程学报， 2012， 25（5）： 556‑563.

WANG Hao， LI Fengfeng， ZONG Zhouhong， et al. Influence analysis of seismic traveling wave for long-span CFST arch bridge［J］. Journal of Vibration Engineering， 2012， 25（5）： 556‑563.

［3］""""""" 闫斌， 戴公连， 徐庆元. 行波效应下铁路简支梁桥梁轨系统地震响应［J］. 振动工程学报， 2013， 26（3）： 357‑362.

YAN Bin， DAI Gonglian， XU Qingyuan. Seismic response of railway track‑bridge system under travelling wave effect［J］. Journal of Vibration Engineering， 2013， 26（3）： 357‑362.

［4］""""""" 贾少敏， 王子琦， 陈华霆， 等. 多点激励下减震桥梁结构抗震可靠度分析的哈密顿蒙特卡洛子集模拟法［J］. 振动工程学报， 2021， 34（2）： 357‑363.

JIA Shaomin， WANG Ziqi， CHEN Huating， et al. Hamiltonian Monte Carlo based subset simulation for reliability analysis of energy‑dissipation bridge structures with viscous dampers under multi‑support seismic excitations［J］. Journal of Vibration Engineering， 2021， 34（2）： 357‑363.

［5］""""""" 贾宏宇， 杜修力， 李晰， 等. 地震作用下高墩铁路桥梁梁体碰撞间隙宽度需求机理分析［J］. 工程力学， 2017， 34（2）： 207‑215.

JIA Hongyu， DU Xiuli， LI Xi， et al. Demand mechanism analysis on pounding separation distance of high pier railway bridges subjected to earthquake excitations［J］. Engineering Mechanics， 2017， 34（2）： 207‑215.

［6］""""""" 何颖， 丁晓凡， 刘中宪， 等. 考虑沉积河谷非线性放大效应的空间相关多点地震动模拟［J］. 工程力学，2023，40（10）： 99‑111.

HE Ying， DING Xiaofan， LIU Zhongxian， et al. Spatial correlated multi‑point ground motion simulation in sedimentary valley considering soil nonlinearity［J］. Engineering， 2023，40（10）： 99‑111.

［7］""""""" 雷虎军， 李书斌， 黄炳坤. 非一致地震激励下大跨铁路斜拉桥车桥耦合振动研究［J］. 地震工程与工程振动， 2022， 42（6）： 213‑221.

LEI Hujun， LI Shubin， HUANG Bingkun. Train-bridge coupling vibration of long‑span railway cable-stayed bridge under non‑uniform seismic excitation［J］. Earthquake Engineering and Engineering Dynamics， 2022， 42（6）： 213‑221.

［8］""""""" 宋光松， 江辉， 郭辉， 等. 行波激励下高烈度区特大铁路悬索桥减震技术研究［J］. 铁道科学与工程学报， 2022， 19（11）： 3303‑3315.

SONG Guangsong， JIANG Hui， GUO Hui， et al. Seismic reduction technology of long‑span railway suspension bridge in high‑intensity area with the action of traveling wave effect［J］. Journal of Railway Science and Engineering， 2022， 19（11）： 3303‑3315.

［9］""""""" LIU Z X， MENG S B， CHENG X L， et al. Efficient simulation of stochastic seismic response of long‑span bridges in river valleys using hybrid BEM‑FEM［J］. Soil Dynamics and Earthquake Engineering， 2023， 165： 107690.

［10］""""" KIUREGHIAN A D， NEUENHOFER A. Response spectrum method for multi‑support seismic excitations［J］. Earthquake Engineering amp; Structural Dynamics， 1992， 21（8）： 713‑740.

［11］""""" NAKAMURA Y， KIUREGHIAN A D， LIU D. Multiple-support response spectrum analysis of the Golden Gate Bridge［R］. UCB/EERC‑93/05. Berkeley， CA： Earthquake Engineering Research Center， University of California at Berkeley， 1993： 1‑78.

［12］""""" HEREDIA‑ZAVONI E， VANMARCKE E H. Seismic random-vibration analysis of multi‑support structural systems［J］. Journal of Engineering Mechanics， 1994， 120（5）： 1107‑1128.

［13］""""" KONAKLI K， KIUREGHIAN A D. Extended MSRS rule for seismic analysis of bridges subjected to differential support motions［J］. Earthquake Engineering amp; Structural Dynamics， 2011， 40（12）： 1315‑1335.

［14］""""" WANG Z Q， KIUREGHIAN A D. Multiple‑support response spectrum analysis using load‑dependent Ritz vectors［J］. Earthquake Engineering amp; Structural Dynamics， 2014， 43（15）： 2283‑2297.

［15］""""" 王君杰， 郭进. 多点地震动激励下的高效反应谱方法［J］. 地震学报， 2022， 44（5）： 810‑823.

WANG Junjie， GUO Jin. An efficient seismic response spectrum method under multi‑support excitations［J］. Acta Seismologica Sinica， 2022， 44（5）： 810‑823.

［16］""""" 叶继红， 孙建梅. 多点激励反应谱法的理论研究［J］.应用力学学报， 2007， 24（1）： 47‑53.

YE Jihong， SUN Jianmei. Research of multipoint excitation response spectrum method［J］. Chinese Journal of Applied Mechanics， 2007， 24（1）： 47‑53.

［17］""""" 刘先明， 叶继红， 李爱群. 多点输入反应谱法的理论研究［J］. 土木工程学报， 2005， 38（3）： 17‑22.

LIU Xianming， YE Jihong， LI Aiqun. Research of multi-support response spectrum method［J］. China Civil Engineering Journal， 2005， 38（3）： 17‑22.

［18］""""" 李杰， 李建华. 多点激励下结构随机地震反应分析的反应谱方法［J］. 地震工程与工程振动， 2004， 24（3）： 21‑29.

LI Jie， LI Jianhua. A response spectrum method for random vibration analysis of structures under multi‑support excitations［J］. Earthquake Engineering and Engineering Vibration， 2004， 24（3）： 21‑29.

［19］""""" 刘洪兵， 范立础. 大跨桥梁考虑地形及多点激励的地震响应分析［J］. 同济大学学报（自然科学版）， 2003， 31（6）： 641‑646.

LIU Hongbing， FAN Lichu. Seismic Analysis of long span bridges considering topographic effects and multi-supported excitations［J］. Journal of Tongji University（Natural Science）， 2003， 31（6）： 641‑646.

［20］""""" LI Q， YANG W L. An improved method of hydrodynamic pressure calculation for circular hollow piers in deep water under earthquake［J］. Ocean Engineering， 2013， 72： 241‑256.

［21］""""" 黄信. 水‑桥墩动力相互作用机理及深水桥梁非线性地震响应研究［D］. 天津： 天津大学， 2012.

HUANG Xin. Mechanism of water‑bridge pier dynamic interaction and nonlinear seismic responses of bridges in deep water［D］. Tianjin： Tianjin University， 2012.

［22］""""" 王丕光， 赵密， 杜修力. 任意光滑截面桥墩地震动水压力分析［J］. 振动与冲击， 2018， 37（21）： 8‑13.

WANG Piguang， ZHAO Mi， DU Xiuli. Earthquake induced hydrodynamic pressure on a uniform vertical cylinder with arbitrary smooth cross‑section［J］. Journal of Vibration and Shock， 2018， 37（21）： 8‑13.

［23］""""" 中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局. 建筑抗震设计规范： GB 50011—2010［S］. 北京：中国建筑工业出版社，2010.

Ministry of Housing and Urban‑Rural Development of the People’s Republic of China，AQSIQ. Code for seismic design of buildings： GB 50011—2010［S］. Beijing： China Building Industry Press， 2010.

［24］""""" 李忠献， 李笑穹， 李宁. 空间相关多点多维地震动的模拟［J］. 地震工程与工程振动， 2014， 34（4）： 64‑72.

LI Zhongxian， LI Xiaoqiong， LI Ning. Simulation of multi‑point and multi‑dimension spatially correlated earthquake ground motions［J］. Earthquake Engineering and Engineering Dynamics， 2014， 34（4）： 64‑72.

第一作者： 吴" 堃（1991―），男，博士，副教授。E‑mail： k_wu@cauc.edu.cn

通信作者： 苏俊省（1990―），男，博士，副教授。E‑mail： junshengsu@tju.edu.cn

基金项目："国家自然科学基金重点项目（52238012）；天津市教委科研计划项目（2021KJ055）；中央高校基本科研业务费项目（2000560616）