线性矩法在分布未知条件下的随机结构抗震可靠度分析






摘要: 在工程结构领域,由于数据不足,结构参数的分布通常未知,这成为结构可靠性分析中常见而复杂的挑战。在结构参数分布未知的情况下,本文提出了随机结构抗震可靠度分析的线性矩法。构造了仅由两个基本随机变量描述的随机动力系统:(1)基于结构随机参数的前四阶线性矩,借助标准正态分布随机变量的随机函数表达,将结构参数的随机变量表示为仅有一个基本随机变量的一元三次多项式;(2)利用一个基本随机变量的随机函数‑谱表示模型描述非平稳地震动过程。在此基础上,根据数论方法确定两个基本随机变量的代表点集,进行时程分析并计算结构响应极值,进而计算确定界限下功能函数的样本及其线性矩;利用功能函数的前四阶线性矩求解三次多项式转换系数;并根据一元三次方程根的求解,建立基于线性矩的结构抗震可靠指标表达式。以结构参数分布未知的非线性单自由度为例说明了本文方法的应用,同时与Monte Carlo模拟结果对比,验证了本文方法的精确性。
关键词: 抗震可靠度; 随机结构; 线性矩; 分布未知; 随机函数-谱表示
中图分类号: TU311.3;O324""" 文献标志码: A""" 文章编号: 1004-4523(2025)01-0180-11
DOI:10.16385/j.cnki.issn.1004-4523.2025.01.020
Seismic reliability analysis of random structures using linear moments method under unknown distributions conditions
WU Luocheng1, ZHANG Longwen2, Zeng Menglan1
(1.College of Civil Engineering, Hunan University, Changsha 410082, China;2.College of Water Resources and Civil Engineering, Hunan Agricultural University, Changsha 410128, China)
Abstract: In the realm of engineering structures, the distribution of structural parameters often remains uncertain due to a lack of sufficient data, presenting a common and intricate challenge in structural reliability analysis. This paper presents a novel linear moment method for assessing the seismic reliability of random structures with unknown distributions. A random dynamic system is constructed using only two basic random variables: (1) the first four-order linear moments derived from the structural random parameters, expressed as a univariate cubic polynomial with a random function involving standard normal random variables; (2) A random function-spectral representation model is utilized to describe the non-stationary seismic ground motion. On this basis, representative point sets for the two basic random variables are determined using number-theoretical methods. Through time-domain analysis, extreme structural responses are computed to evaluate the samples of the performance function and its linear moments within the specified limit state. The seismic reliability index derived from linear moments is established by solving the univariate cubic equation roots. To demonstrate the proposed method’s applicability, a nonlinear single-degree-of-freedom system with unknown parameter distributions is analyzed, and its effectiveness is verified by comparing the results with those obtained using Monte Carlo simulation.
Keywords: seismic reliability;random structures;linear moments;unknown distributions;random function-spectral representation
地震作用具有破坏性与强烈的随机性,使得工程结构在使用期间可能会受到地震影响。与此同时,结构系统本身的参数(如质量、弹性模量、泊松比、刚度等)也具有不确定性或随机性。因此,进行随机结构参数的抗震可靠度分析对于评估结构性能和确保结构的安全至关重要。寻求高效准确的随机结构抗震可靠度分析方法对于工程结构的安全可靠性评估,提升抗震性能以及减少地震灾害对社会造成的影响具有重要意义。
目前,对于随机结构的分析主要采用随机模拟方法、随机摄动方法和正交展开理论等[1]。随机模拟方法如Monte Carlo模拟(MCS)方法,拉丁超立方抽样LHS方法[2]等,虽然适用范围广泛,但计算量较大;随机摄动方法或正交展开理论则属于数值计算方法。随机摄动方法仅适用于参数变异系数较小的情况;而正交展开理论在求线性结构动力响应时具有较高的精度,但在基函数的选择上存在一些限制,且不能保证收敛性,因此在非线性随机结构的计算精度方面仍有待提高。
在结构抗震可靠度分析方面,首次超越作为结构动力可靠度分析的一种重要失效机制受到众多学者的关注。其中涵盖了离散化的Chapman‑Kolmogorov方程方法[3]、随机平均法[4]、反向Kolmogorov方程[5]以及极值分布方法[6]。概率密度演化方法[7‑8]作为一种广泛使用且有效的基于极值分布的方法,在随机结构动力系统的可靠度问题上具有重要意义。该方法的思路在于将输入(如地震动模型)与结构随机参数(如质量、弹性模量、泊松比、刚度等)建立在一个随机动力系统中,利用在随机系统选点的方法解决首次超越等动力可靠度问题。这为随机结构动力系统解决动力可靠度问题提供了良好的计算框架。近年来,针对随机输入与随机结构的复合可靠度问题,研究者们也试图从条件概率的角度求解随机结构的动力可靠性问题。如杨杰等[9]基于动力响应跨越过程的Markov假设,建立了二阶近似表达式以及基于Kriging模型的数值抽样法。为了解决传统方法在动力响应求解效率与可靠性分析的精度上的不足,基于机器学习建立代理模型,研究了随机结构的动力可靠度问题[10]。相对于响应的概率密度函数,结构响应的统计矩较易获取,从矩的角度(如一次二阶矩法[11]等)进行随机变量的描述并进行随机结构可靠度分析方面的研究也获得了进展。王涛等[12]基于扩展型共轭无迹变换建立了低维与高维的随机系统。尽管对于随机结构问题,研究者们进行了大量的研究,但在复合随机动力可靠度分析的效率与精度平衡上仍有待进一步深入。当然,值得指出的是,MCS方法在理论上能够解决任何动力可靠度问题,但在实际工程中计算成本较高,尤其是在实际的非线性结构分析中可能会出现维度灾难的问题。因此,通常将MCS用作其他方法的校验手段。
为了高效地进行结构随机地震响应分析,寻求高效的地震动输入模型至关重要。通常情况下,地震动输入模型的模拟是基于随机过程理论进行研究的。且往往涉及成百上千的随机变量,因此随机变量的个数或数学模型的维数直接影响地震动合成效率,进而影响随机地震响应分析的效率。基于随机过程理论,SHINOZUKA等[13]提出的谱表示模型因其简单直观、数学基础严密、精确度高等优点,在结构随机地震响应分析中被广泛使用。然而,该模型需要对上百个随机变量进行模拟,极大地增加了实际工程问题分析的难度。为了减少随机变量模拟个数以及提高模拟效率等,陈建兵等[14]提出了随机过程谐和函数表达式,采用少量的项数就可以获得精确的功率谱函数;LIU等[15]采用随机函数思想构造1~2个基本随机变量的随机函数形式,对随机地震动进行模拟。以上研究为结构随机地震响应的高效分析提供了便利。
此外,随机结构分析时往往假设为某一确定分布,然而在实际工程中由于统计数据不足,难以获得结构参数的分布,但较易根据已有的数据统计出参数的前几阶统计矩如中心矩[16]、线性矩[17]。因此,在仅有样本数据的情况下,通过计算统计矩来拟合分布,为分布未知情况下的可靠度分析带来了新的解决思路。对于拟合分布问题,基于高阶统计矩的立方正态变换使用随机变量前四阶中心矩来近似分布,这一方法得到了广泛的应用。例如,Fisher‑Cornish模型[18]、Hermite矩模型[19],四矩标准化函数[20‑21]、统一的Hermite多项式模型[22]等。由于高阶中心矩对于尾部特征有很强的敏感性,在实际工程中,实验数据和实地测量的数据较为有限,因而高阶的中心矩存在较大的不确定性[23]。值得指出的是,在较小的样本规模下线性矩比中心矩更稳健[17, 23],因此基于线性矩的正态变换也得到了一定的关注[24]。尽管线性矩法在不偏性和稳健性方面的优势在评估暴雨和洪水资料序列的极值中得到了广泛应用[25‑26],但其在结构抗震可靠度分析方面的研究还不够深入。从统计矩代替分布函数进行概率分析的观点看来,在较小样本规模下,与中心矩相比,使用线性矩显得尤为重要。基于此,本文试图利用线性矩的正态变换模型,从失效概率与可靠指标的定义出发,建立基于线性矩的结构可靠指标,以实现随机结构的抗震可靠度分析。
本文首先介绍了线性矩的计算及基于线性矩的三次多项式转换。接着提出了一种基于线性矩的随机结构抗震可靠度分析方法,并建立了基于线性矩的可靠性指标表达式。该方法将随机函数‑谱表示模型作为输入,基于线性矩的三次多项式转换建立结构参数分布未知的随机变量,进而将两个基本随机变量集合在一个随机动力系统中。利用两个基本随机变量以及数论选点方法进行非线性时程分析,从而计算结构响应的极值。最后以单自由度非线性结构为例对本文提出的方法进行了说明,给出了详细的计算过程与计算结果,同时利用MCS方法验证了本文方法的精确性。
1 线性矩的计算
1.1 概率分布的线性矩
线性矩由HOSKING[23]提出,定义为概率权重矩的线性组合。对于已知概率分布的连续随机变量X,其累积分布函数和逆函数分别表示为F(X)和X(F)。因此,随机变量X的概率权重矩表示为:
(1)
式中,r=0,1,2,…为概率权重矩的阶数。那么,随机变量X的第r阶线性矩表示为:
(2)
式中,βi(X)(i=0,1,2,…)为根据式(1)获得的概率权重矩,pr,i表示为:
(3)
类似于中心矩,使用线性偏态系数和线性峰度系数描述随机变量X的偏度和峰度:
;(4)
式中,λ2(X)为第2阶线性矩;为第r阶线性矩,当r=3,4时则分别为第3阶与第4阶线性矩。第2阶、第3阶与第4阶线性矩均可以通过式(2)计算得到。
在实际的工程运用中,在分布已知的情况下,根据式(1)和(2)可以获得已知分布的随机变量的前4阶线性矩,表示为:
(5)
(6)
(7)
(8)
1.2 样本的线性矩
在实际工程当中,获取变量的概率分布比较困难,因此变量的分布往往是未知的,但较易获得变量的样本。在这种情况下,可以通过样本估计线性矩。假设为N个从小到大排列的随机样本,则前四阶线性矩λ1X,λ2X,λ3X与λ4X为:
(9)
(10)
(11)
(12)
1.3 基于线性矩的三次多项式转换
当服从某一分布(正态分布与非正态分布)的随机变量X的前4阶线性矩已知时,三次多项式可以表示为[27]:
(13)
式中,U为服从标准正态分布(均值为0,标准差为1)的随机变量;S(U)为含有U的一元三次函数;a、 b、c、d为多项式系数,由如下等式确定[28]:
(14)
(15)
(16)
(17)
式(13)建立了标准正态分布的随机变量与任意某一分布的随机变量的映射关系,当已知某一随机变量的前4阶线性矩时,可以利用式(13)表示标准正态分布随机变量的函数。特别地,在工程实践中,对于某一随机变量的数据可以通过试验获取,进而根据样本试验数据以及式(9)~(12)获得该随机变量的前4阶线性矩。因此,在分布未知的情况下,通过式(13)与随机变量的线性矩可以避免在工程中对随机变量的假定。
2 分布未知条件下的随机结构抗震可靠度分析框架
2.1 基于主点与损失函数的随机函数-谱表示模型
根据Priestley非平稳随机过程渐进谱理论[29],引入演变功率谱密度函数,则非平稳地震动的谱表示为[30]:
(18)
式中,,,其中,为截止频率;ak与bk为独立的标准正态随机变量。
从式(18)中可以看出,模拟地震动时需要个独立的标准正态随机变量即变量向量。为非平稳地震动的功率谱密度函数,表示为:
(19)
式中,ω为圆频率;为时频调制函数,可以采用如下等式计算[31]:
,(20)
其中:
,(21)
式中,参数amf=0.25 s-1,bmf=0.251 s-1,cmf=0.005。
结合随机函数思想[15],即假设任意一组标准正交随机变量为基本随机变量的函数,则ak与bk分别表示为:
;;
=1,2,…,j(22)
式中,在区间服从均匀分布;,通常取值为;与k为一一映射关系。
实际上,根据式(22),利用MCS模拟对基本随机变量产生随机数,可以得到地震动加速度时程样本。然而,为了高效地获取地震动加速度时程样本,有必要利用选点方法提高计算效率。
本文引入ZOPPÈ[32]提出的均匀分布单变量代表点计算公式,将在区间的基本随机变量离散为,并表示为:
;(23)
式中,nsel为代表点的数量。
损失函数的最小值表示为:
(24)
使用损失函数的最小值可以量化使用不同数量的代表点时的误差。此外,根据数论方法[33‑34]并考虑鲁棒估计,代表点的数量nsel可以确定为144、377、610、987以及1597等。因此,将式(23)与(24)代入式(18),可以获得地震加速度时程的代表性样本()。
2.2 基于线性矩的结构参数随机变量表达
当考虑结构参数(质量、弹性模量、泊松比、刚度等)不确定时,此时可以在LIU等[35]构造的标准正态随机变量的基础上将随机变量表示为一个基本随机变量的形式。设αs与βs为一组不相关的标准正态随机变量,它们可以表示为:
,
(25)
式中,为标准正态分布函数的逆函数;为基本随机变量,在[0,2π]区间服从均匀分布。
当一组不相关的随机变量服从正态分布,且它们的均值分别为与,变异系数分别为与时,可以将表示为:
,(26)
类似地,当有Nr组不相关的随机变量时,Nr组不相关的标准正态随机变量表示为:
,
(27)
式中,()与j()为一一映射关系,其计算方法同k与的一一映射关系。
当结构的参数为非正态随机变量或随机变量分布未知的情况下,本文利用线性矩的三阶多项式即式(13)建立非正态随机变量与正态随机变量的关系。设一组非正态随机变量相互独立,的前4阶线性矩分别为、、、,的前4阶线性矩分别为、、、,则:
,
(28)
式中,、、、为计算随机变量的多项式系数;、、、为计算随机变量的多项式系数。随机变量和的多项式系数求解可以利用它们的前4阶线性矩代入式(14)~(17)求得。对于非正态分布的前4阶线性矩可以根据定义即式(5)~(8)求得。
随机变量的分布未知时,根据式(9)~(12)可以获得其前4阶线性矩。需要指出的是,本文用一个基本随机变量表示结构参数的随机性是针对相互独立的或不相关的随机变量,对于考虑随机变量相关的结构参数的基本随机变量表达还需进一步研究与验证。
为了更加方便地获取常见非正态分布的前4阶线性矩,根据式(5)~(8),表1给出了一些常见分布的参数与前4阶线性矩的关系。当有Nr组不相关的非正态随机变量时,根据式(26)获取Nr组标准正态随机变量后,再根据式(28)计算Nr组非正态随机变量。
表中,F为分布函数;μ和σ分别为分布的均值与标准差;α为分布的尺度参数;ξ为分布的位置参数。在均匀分布中α与β分别为数值中的最小值和最大值。
综上,当不考虑结构参数不确定时,在整个结构分析中,用一个基本随机变量即可实现。当考虑结构参数不确定时,基于随机函数的表达,可以用两个基本随机变量即与表达,此时可以采用好格子点法[36]即glp集合生成均匀散布点集,具体为:令为一个整矢量,满足,及最大公约数(n,hi)=1(i=1,…,s)。令:
(29)
式中,qki表示第k行第i列的元素,;xki为好格子点集第k行第i列的数值。
集合称为生成矢量(n;h1,…,hs)的格子点集。如果Pn在所有可能的生成矢量具有最小偏差,则Pn称为glp集合。xki可以表示为:
(30)
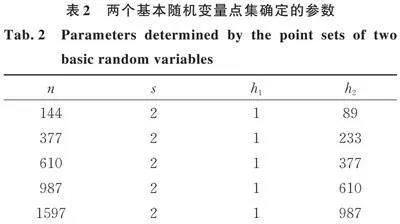
根据好格子点法[36],式(29)与(30)的参数h1、h2、n、s的取值可以根据表2进行选取。
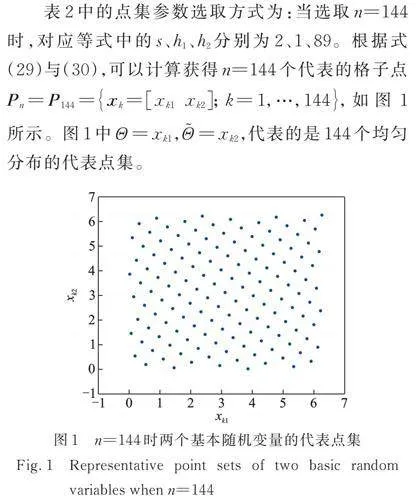
表2中的点集参数选取方式为:当选取n=144时,对应等式中的s、h1、h2分别为2、1、89。根据式(29)与(30),可以计算获得n=144个代表的格子点,如图1所示。图1中,,代表的是144个均匀分布的代表点集。
最后,根据式(18)得到nsel=n条加速度时程后,利用时程分析方法可以计算得到结构的响应时程(如位移响应时程),并逐条统计nsel组响应时程的极值Si()。
2.3 基于线性矩的结构动力可靠指标表达
设结构动力响应的界限为R(一般设为常数),功能函数为G,则功能函数G的表达式为:
(31)
利用式(31)即可计算得到功能函数G的样本数据。接着,根据式(9)~(12)可以计算得到nsel个样本下功能函数G的前4阶线性矩λ1G、λ2G、λ3G以及λ4G。
根据可靠度的定义,功能函数G对应的失效概率Pf可以表示为:
(32)
根据等概率变换,则:
(33)
式中,为标准正态随机变量的累积分布函数;为式(13)的逆函数;M=[λ1G" λ2G" λ3G λ4G]为前4阶线性矩的向量。
接着,式(33)可以表示为:
(34)
根据失效概率与可靠指标的定义,可靠指标可以表示为:
(35)
对于的求解,实质上为求解一元三次方程式(13)的根U。
(36)
对于该方程的求解可根据解析法如盛金公式、卡尔丹公式等进行计算。当判别式时,可以得到方程的一个实根,表达式为:
(37)
其中:
,
,
,,(38)
因此,根据式(35)与(37),本文推导获得的基于前4阶线性矩得到的可靠指标βLM为:
(39)
当判别式时,U可以表示为:
(40)
式中,,其中(Agt;0,-1lt;γlt;1)。
类似地,此时可靠指标βLM表示为:
(41)
2.4 本文提出的线性矩法的分析步骤
基于上述2.1~2.3节分析,本文建立了随机结构抗震可靠度线性矩法的分析步骤,其实施流程如图2所示:
(1) 生成非平稳随机地震动模型。利用一个基本随机变量,以及随机函数谱表示模型生成非平稳随机地震动。
(2)分布未知(已知前4阶线性矩)的结构参数的随机变量表达。利用另一个基本随机变量,获取标准正态分布随机变量,进而利用其前四阶线性矩表达该分布未知的随机变量。
(3) 构造2个基本随机变量(, )的随机动力系统并进行结构分析。在2个基本随机变量描述的随机动力系统中进行非线性时程分析,计算结构的响应极值S。
(4) 根据结构分析计算功能函数G的前4阶线性矩λ1G、λ2G、λ3G、λ4G设定界限R,求解功能函数G=R-S的前4阶线性矩。
(5) 计算基于线性矩λ1G、λ2G、λ3G、λ4G的可靠指标。将功能函数的前4阶线性矩代入式(14)~(17),求解多项式系数a、b、c、d,进而根据式(39)或(41)求解基于线性矩的可靠指标βLM。
3 算例分析
考虑非平稳随机地震激励下的非线性单自由度体系如图3所示,非线性为双线型恢复力模型即恢复力fs‑位移x的关系曲线如图4所示。其中xy为屈服位移,设为0.01 m。k1与k2分别为初始刚度和折减后刚度,折减系数即k1/k2=0.2。
该单自由度体系的运动方程为:
(42)
式中,m、、k分别为体系的质量、阻尼系数、刚度;、、分别为体系的相对加速度、相对速度、相对位移,它们是关于时间t的函数。
本文考虑结构参数m与k1的分布未知,但能够通过样本数据获得其前4阶线性矩。为了获得参数的前4阶线性矩,假设m为正态分布,k1为耿贝尔分布,进而根据其定义获得不确定性参数的分布信息如表3所示。另外考虑阻尼系数= 36612 N∙s/m。根据表3中的前4阶线性矩可以计算得到多项式系数如表4所示。
其功率谱密度函数采用Clough‑Penzien谱[37]:
(43)
式中,和分别为场地土的卓越圆频率和阻尼比;和为地震加速度时程低频分量的参数,, ;S0为基岩地震动加速度白噪声功率谱密度,它反映地震动的强弱程度,也简称为谱强度因子,表示为:
(44)
式中,为地震地面加速度最大值的均值;为峰值因子。Clough‑Penzien谱的参数取值如表5所示,其中,T为地震波持续总时间。
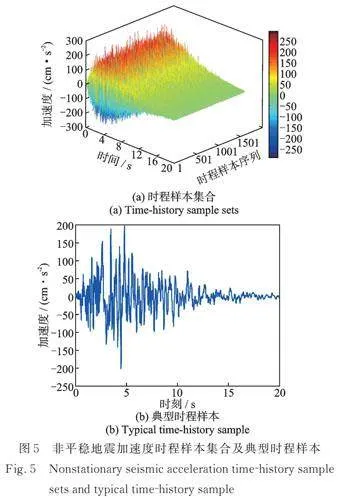
基于随机函数谱表示模型,利用2个基本随机变量生成非平稳地震加速度时程样本(本算例选取1597个点),图5为1597条非平稳地震加速度时程样本集合及典型时程样本。
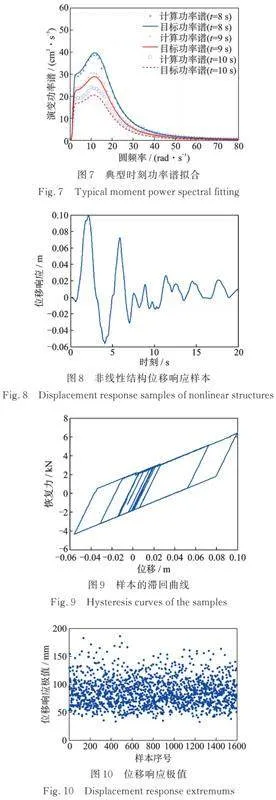
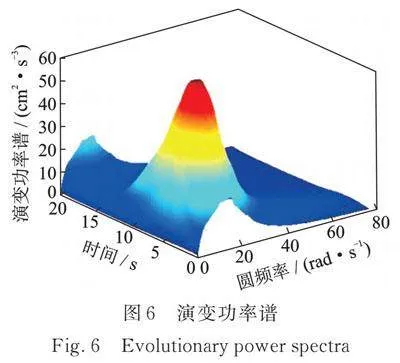
接着,根据小波‑伽辽金方法[38],计算得到演变功率谱如图6所示。图7为根据演变功率谱得到的典型时刻即t=8,9,10 s的功率谱。从图7中可以看出,虽然个别点拟合度较差,但整体曲线的计算功率谱与目标功率谱能够很好地拟合。对于个别点精度低的问题,特别是在10 s时可以通过增加模拟的样本数提高拟合的精度。
最后,根据非线性时程分析方法将1597条地震加速度时程进行逐条分析,计算得到的非线性结构位移响应样本如图8所示。图9给出了一次输出样本的滞回曲线(恢复力‑位移曲线)。从图9中可以看出滞回曲线具有明显的双线型特性。利用本文方法得到位移响应极值的样本点如图10所示。
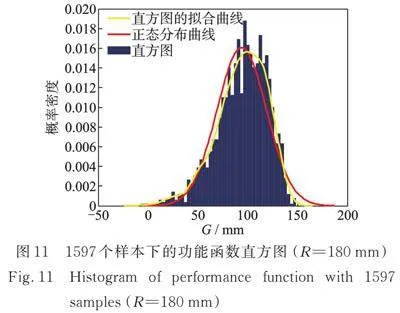
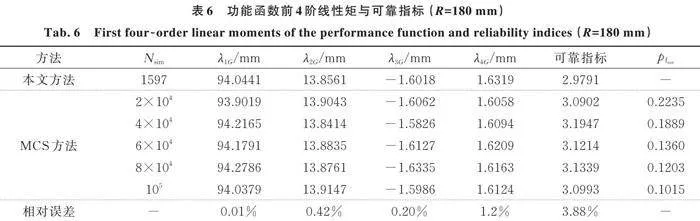
设定界限R=180 mm,利用本文方法计算得到功能函数的前4阶线性矩如表6所示。图11为1597个样本下的功能函数直方图。从图11中可以看出,功能函数拟合分布与正态分布有一定的差异,说明功能函数的分布反映出一定的非正态特性。从图11中可以分析得到,功能函数的非正态分布特性利用其前4阶线性矩表达,反映了利用标准正态随机变量的三次多项式即式(13)表达的有效性与映射关系。为了将本文方法计算结果与MCS方法计算结果对比,表6给出了不同样本下MCS方法计算结果。从表6中可以看出,样本数为105时的计算结果比样本数为2×104~8×104时的结果稳定;同时计算失效概率pf的变异系数,其中,,βMCS为MCS模拟获得的可靠指标,Nsim为模拟的样本数,失效概率的变异系数控制在15%以内。因此,本算例将105次MCS方法计算结果作为校验值进行验证。利用本文方法,根据获得的位移响应极值计算功能函数的前4阶线性矩与可靠指标,结果如表6所示。从表6中可以看出,本文仅需1597个样本点,其前四阶线性矩与可靠指标均与MCS方法计算结果很好地拟合,前四阶线性矩的最大相对误差为1.21%,可靠指标的相对误差为3.88%。
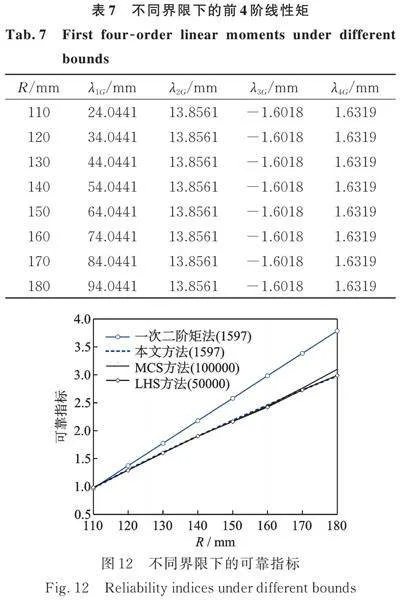
为了进一步说明本文方法的精确性,表7给出了不同界限下的前4阶线性矩。从表7中可以看出,随着界限的增大,第1阶线性矩即均值随之增大,第2、3、4阶线性矩保持不变。图12给出了不同界限下本文方法(1597个样本)、一次二阶矩法(1597个样本)、超拉丁抽样LHS方法(50000个样本)与MCS方法(100000个样本)计算的可靠指标。从图12中可以看出,在不同界限下,本文方法、LHS方法以及MCS方法计算结果曲线拟合良好,而一次二阶矩法由于只用了前2阶中心矩的信息,在界限不断增大时,与MCS方法及LHS方法计算结果的差异逐渐增大。尽管LHS方法与MCS方法能够保证精度,但本文方法在1597个样本下仍能保持与LHS方法及MCS方法同样的精度,体现了本文方法的高效性。值得注意的是,在图12中当界限R=180 mm时,本文方法计算结果与MCS方法计算结果产生了一定的偏差,可以预测本文方法在计算高可靠指标时可能会存在一定的误差。存在的问题可能在于通过本文方法计算的前4阶线性矩与MCS方法计算结果存在一些差异,导致可靠指标也随之产生差异。针对该问题,可以通过增加计算样本点来提高精度。
4 结" 论
本文考虑结构参数分布未知的情况,将基于线性矩的一元三次多项式与降维表示的随机函数‑谱表示模型结合,构造了2个基本随机变量的随机动力系统,提出了一种随机结构抗震可靠度的线性矩法,建立了分布未知条件下的随机结构抗震可靠度分析的方法论框架。通过构造描述随机动力系统的2个基本随机变量,并运用数论方法确定其代表点集,本文方法能够有效地计算结构响应的极值和功能函数的样本及线性矩。通过求解一元三次方程的根并基于可靠度的定义,提出了基于线性矩的结构抗震可靠指标表达式。本文还通过非线性单自由度算例分析,研究了在结构参数分布未知情况下的问题,展示了所提方法的实际效用。具体结论如下:
(1)以线性单自由度为例,考虑随机结构参数时仅需2个基本随机变量,且通过好格子点集能够表示2个基本随机变量。利用基本随机变量生成了1597条地震加速度时程,并在此基础上进行非线性随机地震响应分析。通过分析获得了结构的位移响应以及位移响应极值,并进一步计算了确定界限下功能函数的前4阶线性矩。
(2)通过将本文方法得到的结果与传统的MCS方法,LHS方法以及一次二阶矩方计算结果进行对比,表明利用本文方法获得的功能函数前4阶线性矩及可靠指标均能很好地与MCS方法计算结果拟合,验证了方法的精确性。这为解决随机结构抗震可靠性分析问题提供了一种可行的途径。
(3)总体来看,本文构建了结构参数分布未知下前4阶线性矩的随机结构抗震可靠度分析框架。虽然目前的研究仅涵盖了单自由度系统,但该方法可以推广至多自由度非线性结构分析中。然而,对于高可靠性(或小失效概率)以及不同非线性情况(包括不同滞回恢复力模型),仍需要进一步深入研究和探索。
参考文献:
[1]""""""" GHANEM R G, SPANOS P D. Stochastic Finite Elements: A Spectral Approach[M]. New York: Springer-Verlag, 1991.
[2]""""""" 熊学玉, 顾 炜. 基于改进LHS方法的预应力混凝土结构长期性能概率分析[J]. 工程力学, 2010, 27(4): 163-168.
XIONG Xueyu, GU Wei. Long-term performance probabilistic analysis of PC structure based on improved lhs method[J]. Engineering Mechanics, 2010, 27(4): 163-168.
[3]""""""" IOURTCHENKO D, MO E, NAESS A. Reliability of strongly nonlinear single degree of freedom dynamic systems by the path integration method[J]. Journal of Applied Mechanics, 2008, 75(6): 061016.
[4]""""""" 朱位秋. 随机平均法及其应用[J]. 力学进展, 1987, 17(3): 342-352.
ZHU Weiqiu. Stochastic averaging methods and their applications[J]. Advances in Mechanics, 1987, 17(3): 342-352.
[5]""""""" DOS SANTOS K R M, KOUGIOUMTZOGLOU I A, SPANOS P D. Hilbert transform-based stochastic averaging technique for determining the survival probability of nonlinear oscillators[J]. Journal of Engineering Mechanics, 2019, 145(10): 04019079.
[6]""""""" CHEN J B, LI J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters[J]. Structural Safety, 2007, 29(2): 77-93.
[7]""""""" CHEN J B, YANG J Y, LI J. A GF-discrepancy for point selection in stochastic seismic response analysis of structures with uncertain parameters[J]. Structural Safety, 2016, 59: 20-31.
[8]""""""" 李杰, 陈建兵. 随机动力系统中的概率密度演化方程及其研究进展[J]. 力学进展, 2010, 40(2): 170-188.
LI Jie, CHEN Jianbing. Advances in the research on probability density evolution equations of stochastic dyanmical systems[J]. Advances in Mechanics, 2010, 40(2): 170-188.
[9]""""""" 杨杰, 马萌璠, 王旭. 随机结构动力可靠度计算的条件概率方法[J]. 工程力学, 2018, 35(增刊1): 17-21.
YANG Jie, MA Mengfan, WANG Xu. Conditional probability method for dynamic reliability calculation of random structures[J]. Engineering Mechanics, 2018, 35(Sup1): 17-21.
[10]""""" 姜浩. 基于机器学习的随机结构动态可靠性研究[D]. 西安: 西安电子科技大学, 2021.
JIANG Hao. Research on dynamic reliability of random structures based on machine learning[D]. Xi’an:Xidian University, 2021.
[11]""""" 袁修开, 孔冲冲, 顾健. Kriging与改进一次二阶矩融合的可靠性分析方法[J]. 国防科技大学学报, 2020, 42(6): 150-156.
YUAN Xiukai, KONG Chongchong, GU Jian. Reliability analysis approach based on Kriging and advanced first-order second moment method[J]. Journal of National University of Defense of Technology, 2020, 42(6): 150-156.
[12]""""" 王涛, 李正良, 范文亮. 基于扩展型共轭无迹变换的随机不确定性传播分析方法[J]. 工程力学, 2021, 38(8): 15-23.
WANG Tao, LI Zhengliang, FAN Wenliang. An uncertainty propagation analysis method for stochastic system based on extended conjugate unscented transform[J]. Engineering Mechanics, 2021, 38(8): 15-23.
[13]""""" SHINOZUKA M, JAN C M. Digital simulation of random processes and its applications[J]. Journal of Sound and Vibration, 1972, 25(1): 111-128.
[14]""""" 陈建兵, 李杰. 随机过程的随机谐和函数表达[J]. 力学学报, 2011, 43(3): 505-513.
CHEN Jianbing, LI Jie. Stochastic harmonic function and spectral representations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 505-513.
[15]""""" LIU Z J, LIU W, PENG Y B. Random function based spectral representation of stationary and non-stationary stochastic processes[J]. Probabilistic Engineering Mechanics, 2016, 45: 115-126.
[16]""""" 赵衍刚, 邹春岳, 冀骁文, 等. 非高斯风荷载极值估计:基于HPM转换过程的经验公式[J]. 北京工业大学学报, 2024, 50(2): 180-186.
ZHAO Yangang, ZOU Chunyue, JI Xiaowen, et al. Extreme value estimation of non-Gaussian wind load: empirical formula of HPM-based translation process[J]. Journal of Beijing University of Technology, 2024, 50(2): 180-186.
[17]""""" 曹爽. 基于线性矩的矿井提升机关键部件渐变和动态可靠性分析方法研究[D]. 徐州: 中国矿业大学, 2023.
CAO Shuang. Study on gradual and dynamic reliability analysis method for key components of a mine hoist based on the linear moment[D]. Xuzhou: China University of Mining and Technology,2023.
[18]""""" FISHER S R A, CORNISH E A. The percentile points of distributions having known cumulants[J]. Technometrics, 1960, 2(2): 209-225.
[19]""""" WINTERSTEIN S R. Nonlinear vibration models for extremes and fatigue[J]. Journal of Engineering Mechanics, 1988, 114(10): 1772-1790.
[20]""" ZHAO Y G, LU Z H. Fourth-moment standardization for structural reliability assessment[J]. Journal of Structural Engineering, 2007, 133(7): 916-924.
[21]""""" ZHANG L W. An improved fourth-order moment reliability method for strongly skewed distributions[J]. Structural and Multidisciplinary Optimization, 2020, 62(3): 1213-1225.
[22]""""" ZHANG X Y, ZHAO Y G, LU Z H. Unified hermite polynomial model and its application in estimating non-Gaussian processes[J]. Journal of Engineering Mechanics, 2019, 145(3): 04019001.
[23]""""" HOSKING J R M. L-moments: analysis and estimation of distributions using linear combinations of order statistics[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1990, 52(1): 105-124.
[24]""""" ZHAO Y G, TONG M N, LU Z H, et al. Monotonic expression of polynomial normal transformation based on the first four L-moments[J]. Journal of Engineering Mechanics, 2020, 146(7): 06020003.
[25]""""" 王莉萍, 王韫喆, 向欣, 等. 基于耿贝尔-线性矩和K-Means算法的短时强降水等级划分研究[J]. 地球物理学报, 2023, 66(8): 3171-3184.
WANG Liping, WANG Yunzhe, XIANG Xin, et al. Research on classification of short-duration heavy rain based on Gumbel-Linear Moment and K-Means algorithm[J]. Chinese Journal of Geophysics, 2023, 66(8): 3171-3184.
[26]""""" 冯婧涵. 小样本极端水文频率分析建模及其应用[D]. 南京: 南京邮电大学, 2023.
FENG Jinghan. Modeling and application of small sample extreme hydrological frequency analysis[D]. Nanjing: Nanjing University of Posts and Telecommunications,2023.
[27]""""" FLEISHMAN A I. A method for simulating non-normal distributions[J]. Psychometrika, 1978, 43(4): 521-532.
[28]""""" TUNG Y K. Polynomial normal transforms in uncertainty analysis[J]. Journal of Applied Probability and Statistics, 2000, 1: 167-174.
[29]""""" PRIESTLEY M B. Evolutionary spectra and non-stationary processes[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1965, 27(2): 204-229.
[30]""""" SHINOZUKA M, DEODATIS G. Simulation of stochastic processes by spectral representation[J]. Applied Mechanics Reviews, 1991, 44(4): 191-204.
[31]""" DEODATIS G, SHINOZUKA M. Simulation of seismic ground motion using stochastic waves[J]. Journal of Engineering Mechanics, 1989, 115(12): 2723-2737.
[32]""""" ZOPPÈ A. Principal points of univariate continuous distributions[J]. Statistics and Computing, 1995, 5(2): 127-132.
[33]""""" LI J, CHEN J B. The number theoretical method in response analysis of nonlinear stochastic structures[J]. Computational Mechanics, 2007, 39(6): 693-708.
[34]""" FANG K T, WANG Y, BENTLER P M. Some applications of number-theoretic methods in statistics[J]. Statistical Science, 1994, 9(3): 416-428.
[35]""""" LIU Z J, RUAN X X, LIU Z X, et al. Probability density evolution analysis of stochastic nonlinear structure under non-stationary ground motions[J]. Structure and Infrastructure Engineering, 2019, 15(8): 1049-1059.
[36]""""" 吕大刚, 贾明明, 李刚. 结构可靠度分析的均匀设计响应面法[J]. 工程力学, 2011, 28(7): 109-116.
LYU Dagang, JIA Mingming, LI Gang. Uniform design response surface method for structural reliability analysis[J]. Engineering Mechanics, 2011, 28(7): 109-116.
[37]""""" CLOUGH R W, PENZIEN J. Dynamics of Structures[M]. NewYork: McGraw-Hill, 1975.
[38]""""" KONG F, LI S J, ZHOU W B. Wavelet-Galerkin approach for power spectrum determination of nonlinear oscillators[J]. Mechanical Systems and Signal Processing, 2014, 48(1-2): 300-324.
第一作者:吴罗成(1983―),男,博士研究生。E-mail: 261631662@qq.com通信作者: 张龙文(1988―),男,博士,讲师。E-mail: zhanglongwen@hunau.edu.cn
基金项目:"国家自然科学基金资助项目(52009040);湖南省自然科学基金资助项目(2022JJ40188);长沙市自然科学基金资助项目(kq2202234);湖南省教育厅科学研究重点项目(23A0176);湖南省研究生科研创新项目(CX20220684)

