镜像隐喻视域下小数概念误解分析

摘 要：学生学习小数比大小时常会出现各式各样的错误，小数比大小时，学生继承了整数比大小、分数比大小和负数比大小的已有知识和经验，出现了基于“整数规则”比较大小、“分数规则”比较大小、“零规则”比较大小、“负数规则”比较大小等各种错误.小数比大小混淆是学生在不同的类比映射下，将镜像隐喻同一特征的不同对象合并或不区分的结果.多位国内外学者阐述了物体集合隐喻、对象建构隐喻、量尺隐喻、沿路线运动隐喻、镜像隐喻，他们的隐喻思想研究对研究学生的认知规律提供了新的视角．

关键词：小数比大小；错误；意象图式；镜像隐喻

1 小数的历史

数学家刘徽在注解《九章算术》时提出了用十进制小数表示平方根的非整数部分思想.^［1］刘徽对长度的记法采用的单位是丈、尺、寸、分、厘、毫、秒、忽，“忽”是最小的单位，表示不尽根，指出在“忽”以下的第一位，作为以10为分母的分数，第二位数作为以100为分母的分数……刘徽明确指出，加定法如前，求其微数，微数无名者以为分子，其一退以十为母，其再退以百为母，退之弥下，其分弥细，这说明刘徽已明确地使用十进分数“a+b10+c100+……”来表示小数.^［2］刘徽把个位以下无法标出名称的部分称为“徽数”，也就是现在的小数；古人还用“奇零”“余数”“尾数”及“微数”等名称来称呼小数.公元13世纪，我国出现了小数的记法；公元19世纪末期我国才普遍采用十进制小数点.^［3］从本质上说，十进分数与十进小数是没有区别的.但从表达形式和运算过程来说，十进分数是远不及十进小数简洁优越的．

我国古代天文学家用百进位的小数来记录数据，著名科学家何承天编著的《宋书》律历志部分就已大量地记述了如图1所示的数，即用附在整数位后面的小字来表示小数，这对后来我国小数的记法有深远影响．

十一万八千二百九十六二十五118 296.25九万四千三百五十七94 305.17

如图2所示，刘瑾在其音乐著作《律吕成书》中，表示“106 368.631 2”时，把小数部分写低一格，以示与整数部分的区别.类似地，如图3所示，在《丁巨算法》的第十问的演草里，把“钞六十七两六钱八分”记作因为以“两”作为单位，所以钱、分就是小数了．

美国数学史家卡约里（C.Florian）认为十进小数是近代数学史上关于计算基础方面的三大发明（印度计数法、十进分数和对数）之一.^［4］随着人类社会的发展，需要更精确的数量单位来进行度量和运算，小数就是因为开平方运算的需要产生的.1585年，荷兰的数学家斯蒂文（S.Stevin）在《论小数》一文中，用圆圈内的数字表示十进制分数的数位，并将小数应用到计算中，使十进小数有效地参与记数，如2.192，写作21①9②2③^［5］，这极大地促进了小数的普及和推广.1953年，德国数学家克拉维斯（C.Clavius）首先用“.”表示小数点，这个符号比较简明、方便，成为表示小数的一种通用方法^［6］，被人们广泛使用．

在小学数学课程体系中，小数是“数与代数”领域中的重要内容.在小学阶段，以人教版教材为例，学生在小数方面所学的课程内容主要有小数的读法写法、小数的性质及意义、小数的大小比较、小数点的移动引起小数变化、小数的单位换算、小数的近似数、小数加减法竖式计算、整数加法运算定律推广到小数、小数乘法、小数除法等内容，具体分布如下（见表1）．

一方面，小数在“数与代数”领域占有重要地位，与整数、分数、负数、比、百分数的学习有密切的关系；另一方面，小数的知识还广泛应用于数学的其他三大知识领域中，并发挥着重要的作用，如在“图形与几何”领域中计算图形的周长、面积和体积；“概率与统计”领域中计算平均数、中位数以及在“实践活动”中测量物体的长度等．

2 比大小中的常见错误

小学生对于小数的学习并不陌生，小数在日常生活中经常被用于表示或记录某些物体的数据，如人民币、人的身高、物体的长度和质量、学习成绩、天气的气温、人体的体温等事物的数据都用小数来记录.学生对小数有着非常丰富的已有知识和经验，这些经验既可以帮助学生解题，也会给学生解题带来困扰，导致学生在解题时出现错误.小数大小有如下几个比较常见的错误类型：依据“整数规则”比较;依据“分数规则”比较；依据“零规则”比较；依据“负数规则”比较．

学生存在对小数本身的概念误解（Misconception），错误地认为小数是用符号隔开的两个整数^［7］，所以学生会受到已有知识经验的影响，基于“整数规则”或“整数经验”进行比大小.例如，在比较0.056、0.506、0.560、0.56大小时，有学生错误地认为0.560＞0.506＞0.56＞0.056，理由是560＞506＞56，所以0.560＞0.506＞0.56＞0.056；比较0.676 767 67和0.7的大小，学生初学时认为0.676 767 67＞0.7，从直觉看，学生存在“小数越长，小数越大”的误解^［7］，也称数位溢出思想.以上错误说明，初学者尚未建立比较小数大小的方法，即从高位比起.此外，学生继承整数乘法、整数除法的经验进行比较，如认为3.68×0.98＞3.68，3.68÷0.98＜3.68，存在“乘法越乘越大”“除法越除越小”的误解．

除了整数经验会影响小数比大小，分数的经验也对小数比大小有影响.5.62和5.736两个小数比大小的过程中，学生认为5.62＞5.736.学生误认为5.62=562，5.736=5736，因为562＞5736，所以错误地认为5.62＞5.736，即初学者认为小数越短，小数越大，这样的误解也称分母式思维.虽然这样的行为看起来很幼稚，但是初学者确实表现出了这种行为.面对一样长的小数，学生会利用分数比大小的经验，比较小数之间的大小关系，如13＞14，所以误认为0.3＞0.4，把分数比较继承到了小数比较中．

学生存在对小数的概念误解，认为小数就是很小的数，小数是介于0和1之间的数.所以，零越多的小数，小数越小；零越少的小数，小数越大.在0.1和0.100 00的比较中，学生误认为0.1＞0.100 00，这是基于“零规则”比较出现的错误．

关于小数的概念误解还有小数是很小的数，是小于零的数，小数是负数，即0.22被误认为是零以下的负数.国外研究显示，研究者对初一年级的学生进行比较大小的调查，学生会基于负数比大小的经验产生对小数比较的错误思考，学生的理由是-3＞-4，则0.3＞0.4.^［8］

3 隐喻

隐喻，最早可追溯到传统隐喻，传统隐喻主要是修辞隐喻.亚里士多德（Aristotle）是西方修辞学的始祖，他认为隐喻是一个词替代另一个词，表达同一意义的语言手段，即把一事物比作另一事物，从而增强语言表达效果.两个词语分别来自两个不同的域，通过相似性建立隐喻关系.

20世纪30年代之前隐喻的研究始终没有跳出修辞学的窠臼，直到20世纪30年代以后，隐喻研究转向了语义学理论，英国语言学家理查兹（I. Richards）在《修辞哲学》中指出，隐喻不仅仅是一种语言现象，它还是人类的思维方式，日常生活中充满着隐喻，隐喻是把表示两个不同事物的思想放在一起，两种思想相互作用的结果就是隐喻的意义.理查兹突破了传统隐喻只关注到隐喻某些方面的局限性.从根本上讲，他认为隐喻是思想的相互交流，是语境之间的相互作用，人的思想是隐喻的.理查兹突破了传统修辞学仅将隐喻作为修辞的藩篱，提出了人类思想和行为隐喻性概念.^［9］

后来，认知科学兴起，语言学、信息学、人工智能等领域出现，极大地拓展了隐喻的研究领域，美国学者莱考夫（G.Lakoff）和约翰逊（M.Johnson）从认知的角度对隐喻进行研究，在《我们赖以生存的隐喻》一书中阐述了现代隐喻认知观的基本框架.莱考夫和约翰逊认为隐喻不仅是修辞手法和思维方式，还是人类认知、思维、经验、语言甚至是行为的基础，是人类生存的基本方式.^［10］

隐喻是一种认知现象，人类通过外部刺激经过大脑形成互动经验，涉身活动所形成的思维方式用意象图式来表达，意象图式是人类概念化意义建构的认知基础，人类的身体无时无刻处于各式各样的活动之中，身体始终处于与外部客观世界的接触和互动中，意象图式就在这些活动中，给抽象事物赋予具体结构（如图4）.^［11］人类用熟悉的某一领域的经验（源域）来解释抽象的另一领域的经验（目标域）．

莱考夫和约翰逊认为心智本质上是涉身的；思维大多是无意识的；抽象概念大部分是隐喻的.^［12］隐喻是一种认识新概念的工具，具有涉身性，自动地、无意识地渗透在人类思想、语言和行为之中.隐喻映射将人类涉身感觉运动与外部世界互动的体验投射到主观经验中，赋予其意义并理解意义过程.莱考夫和约翰逊说明了人类使用日常语言通过隐喻理解抽象概念，从而证明了隐喻推理是人类思想和交流的基础.^［13］

有学者将隐喻思想应用到数学研究中，通过隐喻来理解抽象概念.例如，“数字是一条线上的点”“等式是一个平衡”，这些实例通过一个熟悉的、具体的源域（线、平衡、框）来查看不太熟悉的目标域（数字、等式、变量）.隐喻的主要特征是一个领域被概念化为另一个领域．

4 镜像隐喻：十进制数的位值表示法的三种心理构造有学者

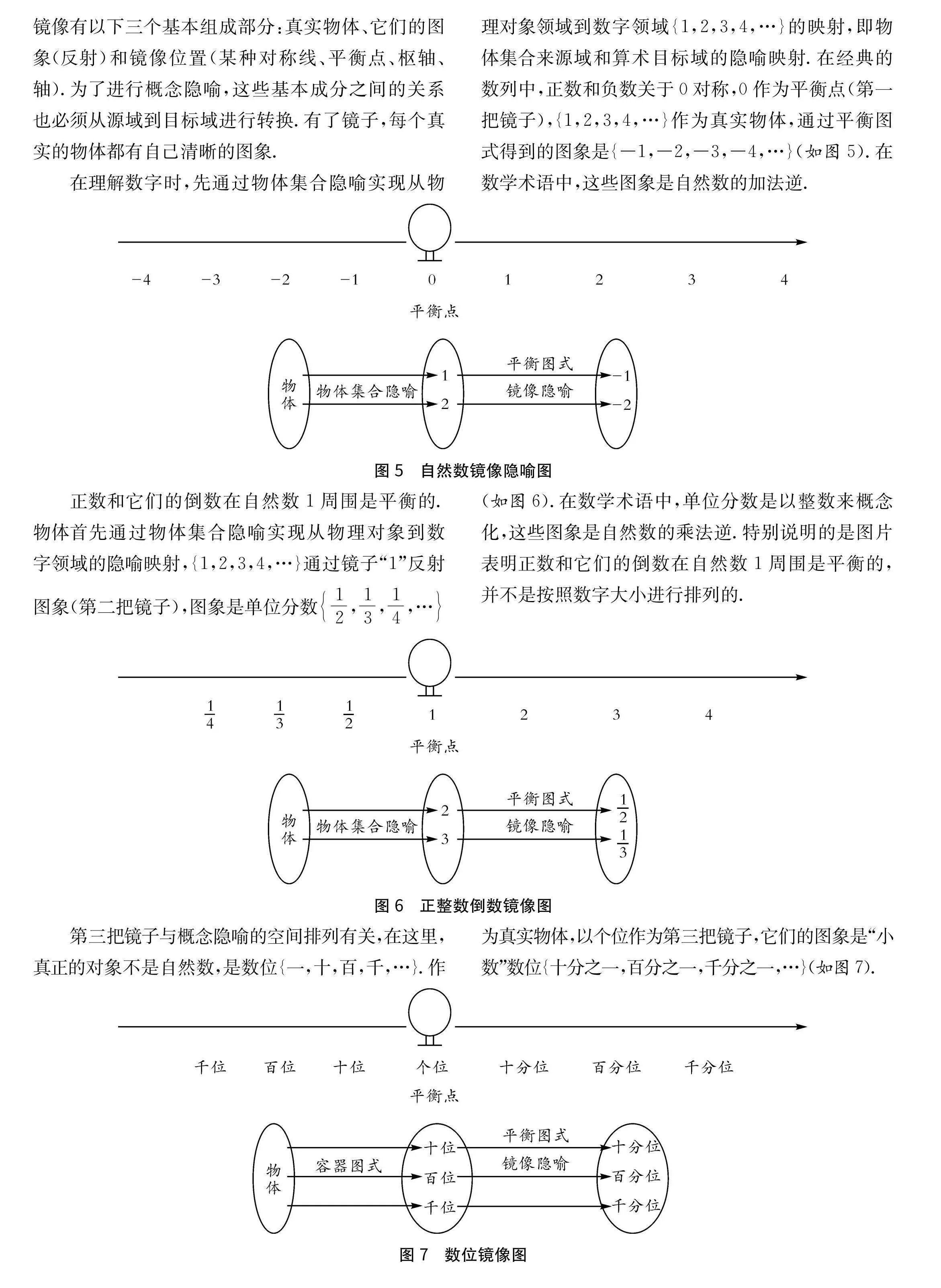
阐述了物体集合隐喻、对象建构隐喻、量尺隐喻和沿路线运动隐喻，人们通过四种基本隐喻对数学的概念进行认知.^［14］镜像隐喻是隐喻的一种，镜像有以下三个基本组成部分：真实物体、它们的图象（反射）和镜像位置（某种对称线、平衡点、枢轴、轴）.为了进行概念隐喻，这些基本成分之间的关系也必须从源域到目标域进行转换.有了镜子，每个真实的物体都有自己清晰的图象.在理解数字时，先通过物体集合隐喻实现从物理对象领域到数字领域{1，2，3，4，…}的映射，即物体集合来源域和算术目标域的隐喻映射.在经典的数列中，正数和负数关于0对称，0作为平衡点（第一把镜子），{1，2，3，4，…}作为真实物体，通过平衡图式得到的图象是{-1，-2，-3，-4，…}（如图5）.在数学术语中，这些图象是自然数的加法逆.

正数和它们的倒数在自然数1周围是平衡的.物体首先通过物体集合隐喻实现从物理对象到数字领域的隐喻映射，{1，2，3，4，…}通过镜子“1”反射图象（第二把镜子），图象是单位分数12，13，14，…（如图6）.在数学术语中，单位分数是以整数来概念化，这些图象是自然数的乘法逆．特别说明的是图片表明正数和它们的倒数在自然数1周围是平衡的，并不是按照数字大小进行排列的.

第三把镜子与概念隐喻的空间排列有关，在这里，真正的对象不是自然数，是数位{一，十，百，千，…}.作为真实物体，以个位作为第三把镜子，它们的图象是“小数”数位{十分之一，百分之一，千分之一，…}（如图7）.

通常的位值计算的空间安排被学生看作是某种“数线”，数字沿着它分布.这个模型和另外两个模型一样，向两个方向无限延伸，小数点的左边有整数值递增，右边有递减值的“十进制数”.学生不清楚镜子的位置，他们认为它是小数点，而不是个位．

自然数是构成其他数概念的主要元素.镜像隐喻涉及分数、负数和十进制数的位值表示法的心理构造，三种心理构造不同.学生把小数和整数、分数、负数混淆的深层次原因是同一源域特征隐喻映射的不同目标之间的混淆，错误地认为小数是负数的学生正在合并自然数的不同图象.

部分学生错误地

合并了第一列和第三列中的图象（见表2），小数比较中继承了分数经验的学生可能合并了第二列和第三列.位值镜像及其相关的“数字线”是一个心理构造，和正/负镜像隐喻、倒数镜像隐喻不同的是位值镜像隐喻是数位的平衡．

5 结论与启示

小数比较中的错误并不是简简单单的粗心、马虎、不认真，也不是简单的看错符号.错误来源于概念本身的误解、概念与概念之间的误解、直觉规律、隐喻过程中出现的混淆等．

首先，学生对小数概念本身存在以下四种常见的概念误解：小数是用符号隔开的两个整数；小数是很小的数；小数是小于零的数；小数是介于0和1之间的数.其次，学生存在概念与概念之间的误解，学生对小数进行比大小时错误地继承了整数经验、分数经验和负数经验，出现了基于“整数规则”比较大小、基于“分数规则”比较大小、基于“零规则”比较大小、基于“负数规则”比较大小等错误.再次，学生存在直觉上的误解，误认为小数越长小数越大，小数越短小数越大，零越少小数越大，乘法越乘越大，除法越除越小.最后，自然数是构成其他数概念的主要元素；镜像隐喻涉及分数、负数和十进制数的位值表示法的心理构造，三种心理构造不同.其中的正/负镜像隐喻和倒数镜像隐喻在正式的数学系统中被识别加法的逆和乘法的逆，但是位值镜像及其相关的“数字线”是一个心理构造，是数位的平衡.小数比大小中的混淆是学生在不同的类比映射下，将镜像隐喻同一特征的不同对象合并或不区分的结果．

参考文献

［1］曹纯.九章算术译注［M］.上海：上海三联书店，2015．

［2］梁宗巨.世界数学史简编［M］.沈阳：辽宁人民出版社，1980．

［3］房元霞.小数的起源与发展［J］.中学数学杂志，2008（6）：65-66．

［4］李迪.十进小数发展简史［J］.数学通报，1964（10）：47-49+16．

［5］郜舒竹.数学的观念、思想和方法［M］.北京：首都师范大学出版社，2004．

［6］谭青兰，袁箭卫.分数与小数的发展简史［J］.湖南教育（数学教师），2008（3）：42-44．

［7］Steinle V. Detection and Remediation of Decimal Misconceptions［J］.Towards Excellence in Mathematics，2004（11）：460-478.

［8］Mehmetlioglu D. Misconception of Elementary School Students about Comparing Decimal Numbers［J］.Procedia Social and Behavioral Sciences，2014（152）：569-574．

［9］朱培.当代隐喻研究概评［J］.黑龙江高教研究，2011（12）：191-192．

［10］乔治·莱考夫，马克·约翰逊.我们赖以生存的隐喻［M］.杭州：浙江大学出版社，2015．

［11］李福印.意象图式理论［J］.四川外语学院学报，2007（1）：80-85.

［12］Lakoff G， Johnson M. Philosophy in the Flesh：The Embodied Mind and Its Challenge to Western Thought［M］.New York： Basic Books，1999．

［13］Lakoff G， Johnson M. Metaphors We Live By［M］. Chicago： University of Chicago Press，1987．

［14］韩大勇.涉身性、隐喻与基本算数——莱考夫涉身认知思想研究［J］.科学·经济·社会，2018（4）：52-58．