小学数学分层作业设计研究

摘" 要：针对小学数学“图形面积”单元的教学难点，特别是复合图形面积计算问题，分层作业设计展现出显著的优势.本文通过分析学生在学习过程中遇到的困难，提出了一套针对不同能力水平学生的分层作业设计方案.实践表明，合理设计的分层作业能有效提升学生解决复杂图形面积问题的能力，为小学数学教师提供了实用的教学策略和具体操作指导．

关键词：小学数学；分层作业；复合图形

图形面积计算是小学数学教育中的重要内容，然而在实际教学中，学生常常遇到诸多困难，尤其是在面对复合图形时.传统的统一作业模式难以满足不同学生的学习需求，导致部分学生遇到挫折，而另一部分学生则缺乏足够的挑战.为应对这一问题，分层作业设计应运而生.本文聚焦于小学数学“图形面积”单元，探讨如何通过分层作业设计来提高教学效果，通过分析学生在学习过程中遇到的典型困难，提出了一套针对不同能力水平学生的分层作业设计方案．

1" 图形面积教学中的问题与挑战

复合图形面积计算是学生常遇到的难点，涉及图形的分解与组合，要求学生具备较高的空间思维能力.［1］许多学生在面对不规则图形时感到困惑，难以正确运用面积公式.学生认知水平的个体差异也给教学带来挑战，有些学生迅速掌握基本概念，而另一些学生则需要更多时间练习.传统的统一作业模式难以满足不同学生的需求，容易使部分学生遇到挫折或缺乏挑战.此外，将理论知识与实际生活联系起来也是一大难题，学生往往不能灵活运用所学知识解决现实问题.这些问题凸显了实施分层教学的必要性．

2" 图形面积单元分层作业设计

2.1" 教学目标的层次划分

图形面积单元的教学目标需根据学生的认知水平和学习能力进行层次划分.基础层目标聚焦于基本概念的理解和简单图形面积的计算，如长方形、正方形和三角形.［2］学生需掌握相关的面积公式并能进行简单的应用.提高层目标要求学生理解和掌握复合图形的面积计算方法，包括图形的分解与组合.学生应能识别复杂图形中的基本构成，并灵活运用已学知识解决问题.拓展层目标则着重培养学生的创新思维和实际应用能力，鼓励学生探索不同解题策略，并能将所学知识应用于实际生活中的面积估算.这种层次划分确保了不同水平的学生都能得到适当的挑战和发展机会．

2.2" 基础层作业设计与示例

设计重点包括单一图形的面积计算、面积公式的记忆和简单应用.典型的作业形式包括填空题、选择题和简单的计算题.［3］例如，给出一个边长为6cm的正方形，要求学生计算其面积；提供一个底边为5cm、高为4cm的三角形，让学生运用公式求解面积.此外，还包括一些图形识别题，如展示多个图形，要求学生指出哪些是正方形、长方形或三角形.这类作业帮助学生建立对基本图形的直观认识，为后续学习奠定基础.基础层作业的难度适中，目的是提高学生的信心，激发学习兴趣．

2.3" 提高层作业设计与示例

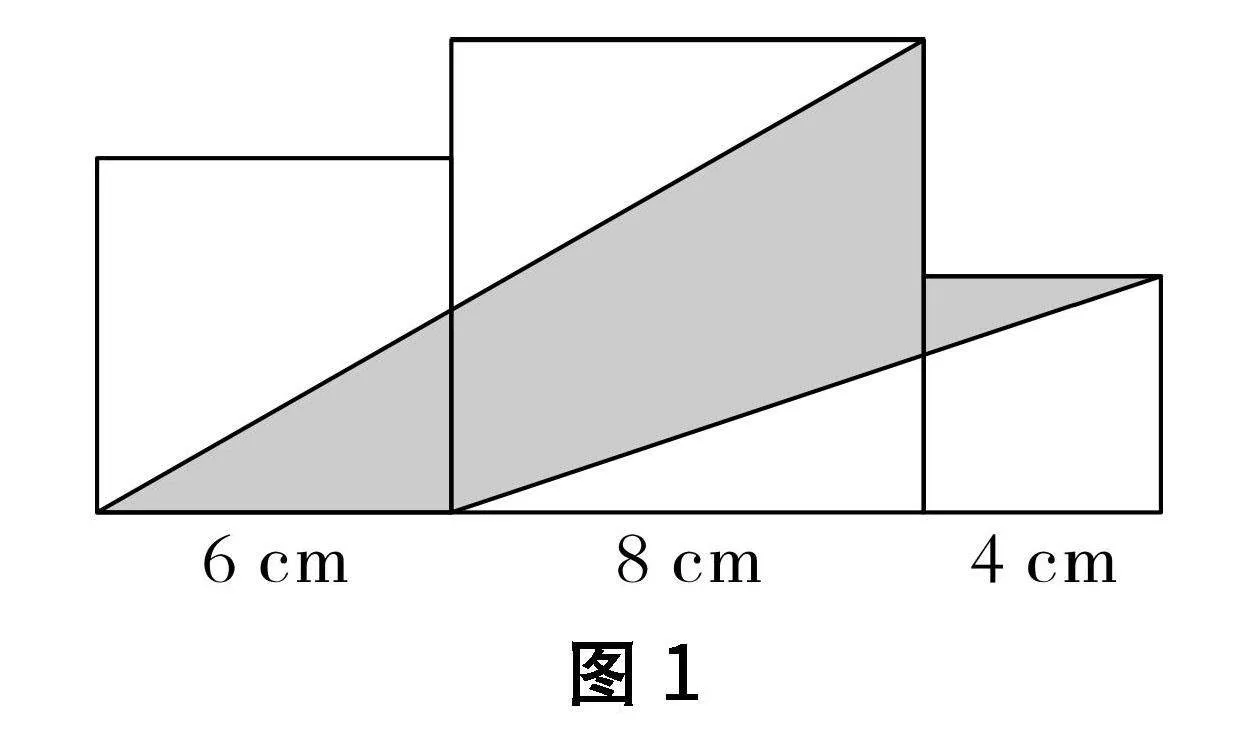
提高层作业聚焦于复合图形的面积计算，旨在提升学生的空间思维和问题解决能力.设计中融入了图形的分解与组合技巧，要求学生灵活运用所学知识.［4］一个典型的例题是给出一个由正方形、长方形和三角形组成的复合图形，要求学生计算其总面积.如图1所示，展示了三个相邻的正方形，边长分别为6cm、8cm和4cm，学生需要计算阴影部分的面积.这类问题要求学生先分析图形结构，再选择合适的计算策略.提高层作业还包括一些需要转化思维的问题，如给出总面积和部分图形的尺寸，要求学生求解未知部分的面积.这些作业培养了学生的逻辑推理能力和创新思维．

图1

3" 分层作业的实施与案例分析

3.1" 复合图形面积计算教学案例

教学案例聚焦于上面的复合图形题.教学开始，教师在黑板上绘制此图形，引导学生观察图形特征，

“看这个图形，我们能识别出哪些熟悉的形状”.学生积极回应，指出正方形.教师继续提问“如何求出阴影部分的面积”，鼓励学生思考多种方法.一名学生提出“可以先算大的面积，再减去不要的部分”，教师肯定这种思路，并在黑板上标注关键数据，引导全班学生一步步分析.

3.2" 分层作业实施过程

针对这个复合图形问题，教师设计了三个层次的作业.对于基础层的学生，教师提供一个图形分解示意图，标明各部分的尺寸，学生需要填写每一步的计算过程.提高层的学生则只获得原始图形，需自行决定解题策略.教师巡视时，对遇到困难的学生提示“试试把图形分成几个部分”.拓展层的学生不仅要解决问题，还需探索至少两种不同的解法.例如，一种方法是计算（4×4＋8×8＋6×8）-（4＋8）×4÷2-8×（8＋6）÷2，另一种是直接计算（14×8）÷2＋4×4-（8＋4）×4÷2.课堂上，教师组织不同层次的学生进行小组讨论，交流各自的解题思路．

3.3" 学生解题策略分析

在解决这个复合图形问题时，学生展现出多样的策略.一组学生采用了直接的加法策略，对第一个正方形作辅助线，使其构成一个长为6cm，高为8cm的长方形，复合图形总面积为4×4＋8×8＋6×8=16＋64＋48=128（cm2），然后减去上、下两个三角形面积，得128-（4＋8）×4÷2-8×（8＋6）÷2=48（cm2）.另一组学生使用了更高效的方法，直接计算左侧两个图形构成的长方形的面积为14×8=112（cm2），然后加上右侧小正方形面积，再减去左上、右下两个三角形面积，得112＋4×4-（6＋8）×8÷2-（8＋4）×4÷2=112＋16-56-24=48（cm2）.教师鼓励学生比较这些方法的效率和适用性．

3.4" 教学效果评估

通过这个复合图形面积的案例，教学效果得到了全面评估.定量分析显示，在后续的类似题目中，学生的正确率从之前的65%提升到了85%.特别是中等水平的学生，在复合图形分解方面的能力显著提升，错误率降低了约30%.定性分析表明，学生解题思路更加多元化.例如，在一道要求计算L形图形面积的题目中，超过60%的学生能够灵活运用至少两种不同的解法.课堂观察发现，在讨论这个案例的过程中，学生参与度明显提高，特别是在小组交流环节，学生间的互动更加积极.一位学生反馈：“以前看到这种题目就害怕，现在感觉有多种方法可以尝试，不那么可怕了.”笔者注意到，虽然教师备课工作量增加，但学生的学习兴趣和课堂参与度的提升使得教学更加顺畅和有效．

4" 教学建议与推广应用

4.1" 分层作业设计的关键要点

以复合图形面积计算为例，基础层作业需聚焦于单一图形的面积计算，如提供一个边长为6cm的正方形，要求计算其面积.提高层作业则引入简单的复合图形，如两个相邻的正方形，边长分别为6cm和8cm，计算它们的总面积.拓展层作业应涉及更复杂的图形组合，如案例中的三个连续正方形问题.关键在于确保各层次之间的难度递进合理，又不失挑战性.设计时应注重问题的开放性，允许多种解法.对于案例中的问题，鼓励学生探索不同的图形分解方法.此外，将实际生活情境融入题目，如设计一个由不同形状组成的花园，能激发学生的学习兴趣和应用意识．

4.2" 实施过程中的注意事项

教师在讲解复合图形面积计算时，应采用由浅入深的方法，从简单的图形面积计算开始，逐步过渡到如案例中的复杂图形.在此过程中，教师要注意观察学生的反应，及时调整讲解节奏.对于理解较慢的学生，教师要提供更多的视觉辅助，如使用彩色粉笔标注不同部分的面积.对于学习较快的学生，教师要鼓励他们探索多种解法，如案例中的直接计算大长方形面积再减去不需要的部分.在小组讨论环节，教师要确保不同层次的学生能互相交流，促进思维的碰撞.评价时，教师不仅要关注结果的正确性，更要重视解题思路的多样性和创新性.同时，建立动态调整机制，允许学生根据表现在不同层次间流动，保持学习的挑战性和积极性．［5］

4.3" 促进分层教学的校级支持措施

学校可以采取以下措施：①组织教研活动，让教师分享分层作业设计的经验，如讨论复合图形面积计算案例的不同设计方案；②建立资源共享平台，收集各类分层作业题目，方便教师选用和改编，如将案例中的三连正方形问题拓展为不同难度的版本，供其他教师参考；③提供专业培训，邀请专家讲解分层教学的理论和实践，提升教师的课程设计能力；④鼓励跨学科合作，如数学教师与美术教师合作，设计结合几何图形的创意作业；⑤在教学评价体系中，将分层教学实践纳入考核指标，激励教师积极尝试；⑥配备必要的硬件设施，如数字化教学设备，便于教师展示复杂图形和动态演示解题过程.学校通过这些措施，营造有利于分层教学的校园环境．

5" 结语

分层作业设计在小学数学图形面积单元的应用，展现了其在提高教学效果方面的显著优势.通过案例分析和实践评估可知，这种教学方法能有效提升学生解决复杂图形面积问题的能力，同时增强学生的学习兴趣和自信心.分层作业不仅满足了不同水平学生的学习需求，还培养了学生的多元思维和创新能力.成功实施分层教学需要教师投入更多的时间和精力，也需要学校层面的支持.未来的研究可以进一步探索如何将这种教学方法推广到其他数学单元，以及如何利用信息技术提高分层作业的效率和个性化程度．

参考文献

［1］ 单群贵.极限演绎，让结构化思维走向深刻——以苏教版五年级上册“图形面积期末复习”教学为例［J］.新教师，2018（7）：46-47．

［2］ 曾莲秀.四巧板与图形面积——益智器具与教材内容融合教学课例设计［J］.小学教学研究，2015（22）：48-49．

［3］ 胡静.以简驭繁 化隐为显——《地毯上的图形面积》教学［J］.小学教学设计，2014（26）：34-35．

［4］ 包建恩.解密“图形面积”——小学数学“图形的面积”公式推导的数学方法［J］.新课程（下），2014（2）：120．

［5］ 唐武元.求差、分割、代换——求图形面积的三法宝［J］.数学小灵通（5-6年级版），2010（Z1）：30-31．