遇等腰勿忘分类讨论

分类讨论思想是解题的一种常用思想方法，它有利于培养和发展同学们思维的条理性和缜密性，在解有关等腰三角形的问题时经常用到分类讨论思想，下面举例说明.

一、腰和底不确定需分类讨论

例1 若m，n满足|4-m|+（n-6）2=0，则以m，n为两边长的等腰三角形的周长为______。

解：∵ |4-m|≥0，（n-6）2≥0，|4-m|+（n-6）2=0，

∴ |4-m|=0，（n-6）2=0.

∴ n=4．n=6.

∵ m，n是等腰三角形的两边长，

∴ m可能是等腰三角形的腰长，也可能是底边长．

（1）当m是腰长时，等腰三角形的三边长分别是4，4，6，则周长是4+4+6=14.

（2）当m是底边长时，等腰三角形的三边长分别是4，6，6，则周长是4+6+6=16.

综上可知，等腰三角形的周长是14或16.

二、底角和顶角不确定需分类讨论

例2 若等腰三角形的一个内角为80°，则另外两个角的度数是______．

解：80°的内角可能是顶角，也可能是底角，所以需分类讨论．

（1）当80°的角是顶角时，两底角分别是50°，50°．

（2）当80°的角是底角时，另外一个底角是80°，顶角是20°．

综上可知，另外两个角的度数是50°和50°，或20°和80°．

三、高的位置不确定需分类讨论

例3 已知等腰三角形一腰上的高与另一腰的夹角为60°，则这个等腰三角形的顶角是（ ）．

A．30° B．60°

C．150° D．30°或150°

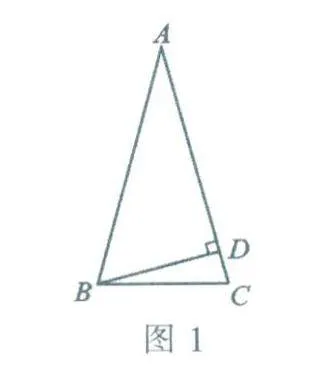
解：（1）当该三角形是锐角三角形时，依题意作图如图1，AB=AC，BD⊥AC于D，∠ABD=60°．

∵ BD⊥AC．

∴ ∠BDA=90°.

∵ ∠ABD=60°．

∴ ∠A =30°.

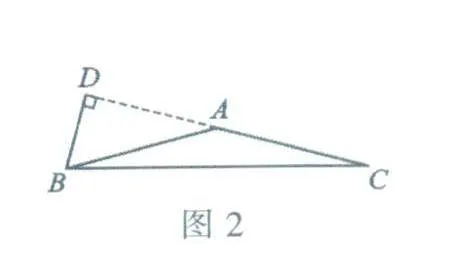
（2）当该三角形是钝角三角形时，依题意作图如图2，AB=AC，BD⊥AC于0，∠ABD=60°.

∵ BD⊥AC于D．

∴ ∠BDA =90°，

∵ ∠A BD=60°．

∴ ∠BAD=30°，∠BAC=150°，

综上可知，这个等腰三角形的顶角是30°或1500.选D．

四、由腰上的中线引出的分类讨论

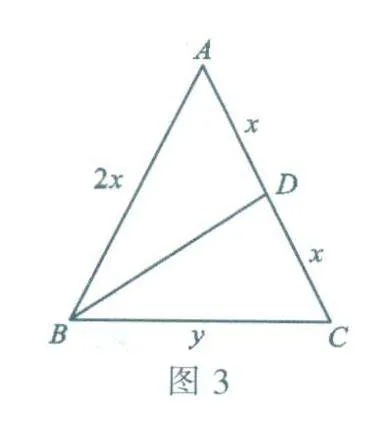
例4 在等腰△ABC中，AB=AC中线BD将这个三角形的周长分为15和12两部分，则这个等腰三角形的底边长为______．

解：依题意画出图形如图3．设A D=CD=x．则AB=AC=2x.设BC=y.

（1）当AB +AD=15，BC+CD=12时，即2x+x=15，y+x=12.解得x=5，y=7.

（2）当AB+AD =12，BC+CD=15时，即2x+x=12，y+x=15.解得x=4，y=11.

综上可知，这个等腰三角形的底边长为7或11.

五、由垂直平分线引出的分类讨论

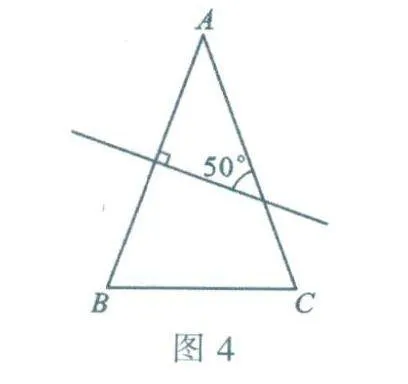
例5 在△ABC中，AB=AC，AB的垂直平分线与AC所在的直线相交所得的锐角为50°，则∠B的度数为______．

解：（1）当△ABC为锐角三角形时，如图4．

∵ AB的垂直平分线与AC所在的直线相交所得的锐角为50°，

∴ ∠A =40°，

∴ ∠B=∠C=70°.

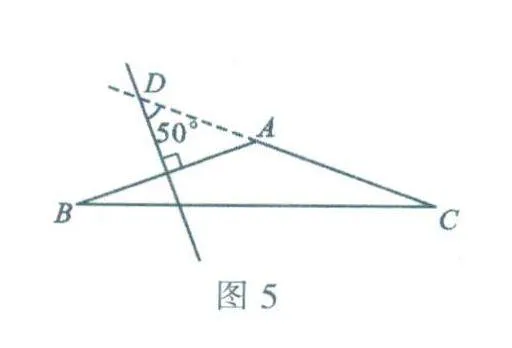
（2）当△ABC为钝角三角形时，如图5．

∵ AB的垂直平分线与AC所在的直线相交所得的锐角为50°．

∴ ∠BAD=40°，∠BAC=140°．

∵ AB＝4C．

∴ ∠B=∠C=20°.

综上可知，∠B为70°或20°.

试金石

1.等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为______.

2．已知等腰三角形的两角之差是30°．求这个等腰三角形的顶角的度数．

3．已知等腰三角形的周长是29，且其一边的长为7．求这个等腰三角形的腰长．

4．△ABC中，AB=AC，CD是AB边上的高，且△ADC为等腰三角形，求∠BCD的度数．

5．等腰三角形的一个外角等于100°，则这个等腰三角形的顶角为多少度？

参考答案

1. 60°或120°

2. 40°或80°.

3. 11.

4. 22.5°或67.5°.

5. 80°或20°．