自主—互动—展评

当前的课程教学改革倡导学生主动参与、乐于探究、勤于动手，培养学生分析和解决问题的能力以及交流与合作的能力。数学，作为基础教育体系中的核心课程，其教学方式的转变，不仅深刻影响着学生核心素养的提升，更在潜移默化中促进学生整体学习方式的革新与优化。初中数学教师要以构建主义理论为指导，辅以信息化技术手段，采用自主实验探索、合作交流的研讨式学习方式，让学生思考问题，获取知识，掌握方法，借此培养学生动手、动脑、动口的能力，使学生真正成为学习的主体。

本节课教学是一个动手作图、动眼观察、动脑猜想、实践验证、巩固应用的动态生成过程，注重学生能力的培养和习惯的养成，采取“自主—互动—展评”式教学方式。同时将“教学反应”型评价和“教学反馈”型评价相结合，促进学生的自主评价，努力推行成功教育、愉快教育的理念，把握评价的时机与尺度，实现评价主体和形式的多样化，从而激发学生的学习兴趣，激活课堂气氛，使课堂教学达到最佳状态。

一、教学目标

1.通过验证等腰三角形的轴对称性，感受几何直观，掌握其相关性质；

2.经历折纸、观察、归纳等活动，发展空间观念和抽象概括能力，感受分类、转化等数学思想方法，不断积累数学活动的经验；

3.训练和培养逻辑推理能力，培养“三会”综合素养。

二、教学过程

1.创设情境——激趣引学

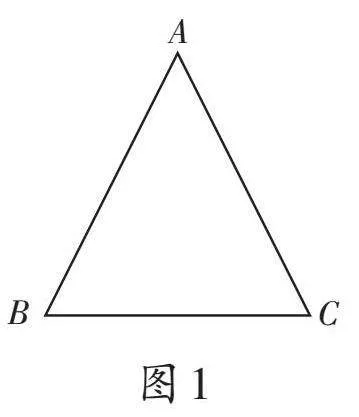
师：同学们，我们已经学过了线段和角的轴对称性，今天这堂课我们来研究等腰三角形的轴对称性。观察图1中的等腰三角形ABC，分别说出它们的腰、底边、顶角和底角。

【设计意图】复习等腰三角形的有关概念，为探索等腰三角形的轴对称性做准备。

2.操作验证——互动研学

师：把该等腰三角形沿顶角平分线对折展开，你有什么发现？

（学生动手操作、实践。）

师：等腰三角形有哪些性质呢？说一说你的猜想。

【设计意图】通过动手操作，学生能够发现等腰三角形是轴对称图形，并找到其对称轴。鼓励学生大胆说出自己对图形的理解和认识，教师作为学生的合作伙伴，适当点拨，帮助学生突破难点。

师：如图1，等腰△ABC，其中AB=AC，请你来证明∠B=∠C。

（学生分组讨论。）

生：过点A作BC边上的高AD，所以∠ADB=∠ADC=90°。然后再根据勾股定理，证明Rt△ADB≌Rt△ADC（HL），最后得出∠B=∠C。作顶角平分线和底边中线同样可以证明。

师：很好。请你用一句话归纳等腰三角形的这个性质。

生：等腰三角形的两个底角相等。

师：这个性质我们可以简称为“等边对等角”。用几何语言表示，即在△ABC中，∵AB=AC，∴∠B=∠C（等边对等角）。

【设计意图】三种语言的转化是定理的具体应用，是规范答题的有效途径，也是对学生识图能力的培养，逐步培养学生的文字语言、图形语言、符号语言的转化能力，为后面运用定理证明打下基础，从而分散难点，让学生能够熟练掌握。

3.运用拓展——展示评学

拓展练习 1.在△ABC中，AB=AC。

（1）如果底角是70°，那么顶角度数是" " ；

（2）如果顶角是70°，那么底角度数是" " ；

（3）如果有一个角等于70°，那么另外两个角度数分别是 ；

（4）如果有一个角等于90°，那么另外两个角度数分别是 ；

2.如图2，在[△]ABC中，AB=AC，点D在BC上，且AD=BD。

（1）图中有几个等腰三角形？

（2）找出图中相等的角并说明理由；

（3）已知[∠B]的度数，你能算出剩余每个角的度数吗？

lt;F：＼制作文件备份＼2024年＼初中生-教研＼初中生教科研2024第11期＼Image＼tu-3.epsgt;[A][B][C][D]

图2

【设计意图】通过课内练习，巩固等腰三角形的性质，激发学生的探究欲望，培养学生将知识应用于实践的能力。在此基础上，进一步培养学生的绘图意识，提炼数学思想方法，如数形结合和分类讨论。

4.探索发现——内化深学

师：在证明∠B=∠C的过程中，同学们运用了多种添加辅助线的方法。你们发现这三条线段在等腰三角形中的特殊位置吗？

生：三条线段重合。

师：什么是三条线段重合？是不是说当我知道这条线段是等腰三角形的顶角平分线时，就能说它也是底边上的高或者中线？

生：是的。

师：很好。请同学们用一句话归纳等腰三角形的这个性质。

生：在等腰三角形中，顶角的平分线、底边上的高以及中线这三条线段是相互重合的。

【设计意图】通过提问，为学生提供充分的独立思考和交流机会，鼓励学生亲自操作和探究，重视知识的生成和形成过程。这样，学生不仅能够成为学习的参与者和研究者，还能掌握数学知识，积累数学活动经验。通过亲自探索和发现等腰三角形的“三线合一”性质，学生能够感受到成功的喜悦，并逐步对观察和操作得出的结论进行抽象概括，实现“三种语言”的相互转换。

5.总结提炼——反思悟学

师：请同学们回顾反思一下，通过本节课的学习，你有哪些收获与感想？

【设计意图】小结的目的在于帮助学生及时巩固所学知识，使之条理化、清晰化，实现自我反馈，进而构建知识体系，形成知识与活动经验的结合。

三、教学反思

“等腰三角形的轴对称性”这部分内容在初中数学中起着比较重要的作用。它是在学生学习了三角形的有关知识，掌握了全等三角形的判定及性质和轴对称性质的基础上进行的，既是对前面所学知识的综合应用，也是后面研究等边三角形等内容的预备知识，同时也是今后证明角相等、线段相等及两直线垂直的重要依据。掌握等腰三角形及其性质在日常生活中的应用，对学生理解数学的实用价值，感悟数学从实践中来并能对实践产生积极反馈具有重要意义。在教学实践中，应致力于构建以学生为中心的数学课堂教学模式，即“自主—互动—展评”教学。

自主：自主合作与分享帮助之意。本案例教学将数学学习的主动权和主要学习过程交给学生，让他们在自主互助、合作探究中进行学习。在上课前让学生通过个人自主预学和小组内资源共享，达成对文本较为详尽的理解，然后在课堂上把小组的学习收获与全班同学分享，并接受其他同学的质疑，从而在研讨中实现对文本的深入研读和理解，以达到预期的教学目的。在教与学上体现以学生为中心，贯穿教学设计、教学实施、教学反馈、教学评价、教学反思全过程。

互动：特指教学过程中的互动交流，涵盖了“师生互动”与“生生互动”。前者涉及教师与学生之间的双向沟通和交流活动，在本课程的教学中，主要展现了教师的引导作用与学生的主体地位；而后者则指的是学生彼此间的多向互动，重点体现了学生的“参与精神”。

展评：将学生的学习成果通过学生现场操作或教师利用展台、多媒体等多种手段先展示出来，然后再进行针对性的评价激励。以此为抓手，不断给学生“赋能”。既避免教师无根据的“虚假”评价，又可形成“扬长避短”的积极学习氛围，促进学生更有效、更良好、更和谐地发展。

“自主—互动—展评”式教学运用了新课程中“自主探究、交流互动、有效评价”的教学理念和对话教学理论，在数学课堂教学观察基础上，针对学生被动学习的现状，促进师生之间自主探究、互助共进，促进生生之间交流互动、互评共进，从而提高课堂教学质量，促进师生共同发展。

（作者单位：江苏省宿迁市宿城区新区初级中学）