非线性Benjamin-Bona-Mahony-Burgers方程的非协调有限元超收敛分析

摘 要：文章研究了二维非线性Benjamin-Bona-Mahony-Burgers （BBMB）方程的非协调有限元方法。利用非协调[EQrot1]元相容误差比插值误差高一阶的特殊性质，给出了非线性BBMB方程在半离散以及向后Euler全离散格式下的超逼近和整体超收敛结果。最后，通过数值试验验证了理论分析的正确性和方法的有效性。

关键词：非线性BBMB 方程；非协调[EQrot1]元；半离散格式；向后 Euler全离散格式；超逼近和超收敛

中图分类号：O241.82" 文献标识码：A" " "文章编号：1007 - 9734 （2024） 02 - 0102 - 06

0 引 言

非线性偏微分方程又称非线性数学物理方程和非线性演化方程，是用于描述力学、化学及循环系统、流行病学等现代科学和工程领域中非线性现象的数学模型。其中的非线性BBMB方程 常用来描述具有耗散效应的小振幅长波在非线性色散介质中的传播。

本文考虑如下的二维非线性BBMB方程：

[ut−αΔut−βΔu+∇⋅u+u∇⋅u=0， （X， t）∈Ω×（0，T]u（X，t）=0，" " " " " " " " " " " " " " " " " （X，t）∈∂Ω×（0，T]u（X，0）=u0（X），" " " " " " " " " " " " " " "X∈Ω]（1）

其中[Ω⊂R2]是一个凸的有界多边形区域，边界记为[∂Ω]，[αgt;0， βgt;0， 0lt;Tlt;∞， X=（x，y）]，[Δ]和[∇]分别表示二维拉普拉斯算子和散度算子，[u0（X）]为已知光滑函数。当 [α=1， β=0]时，方程（1）为Benjamin-Bona-Mahony （BBM） 方程；当 [α=0， β=1]时，方程（1）为Burgers方程。关于这两类方程已有较多的研究（见文献［1-4］）。

由于方程（1）的非线性很难得到其真解，因此人们考虑了许多数值求解方法：文献［5］给出了一种Crank-Nicolson型有限差分方法，文献［6］给出了三次样条法，文献［7］给出了有限元方法，文献［8］研究了无网格方法。众所周知，有限元方法中，超收敛是提高解的精度的一种重要手段。其主要原理是基于有限元近似解与精确解的插值之间的误差比传统误差阶数更高（这种特性被称为超逼近），再结合积分恒等式技巧，在不改变现有有限元程序的情况下，通过添加简单的后处理来获得整体超收敛。随后，超收敛分析被广泛应用于各种实际工程数值计算中 （见文献［9-12］）。然而，到目前为止，关于BBMB方程的超收敛的研究还很少。

通常情况下，非协调元相对于协调元来说构造更简单，并具有更好的收敛效果。对于非协调[EQrot1]元来说，其相容误差比插值误差高一阶，同时其插值算子等同于投影算子，这两个性质使得其在某些问题中可以达到更高的精度，因此该单元成为解决一些非线性偏微分方程的有效工具。

本文主要将非协调[EQrot1]元应用于求解非线性BBMB方程，利用该单元的良好性质，分别在半离散和向后Euler全离散格式下给出了高精度分析。具体安排如下：在第1节中，介绍了有限元的空间构造和相关引理；第2节给出了半离散格式下的超逼近和超收敛结果；第3节探讨了向后Euler全离散格式下的超逼近和超收敛分析；最后一节给出了数值算例来验证理论分析的正确性。

1 有限元空间构造

记[Wk，p（Ω）]为标准的 Sobolev 空间，令[Hk（Ω）=Wk，2（Ω）]，[H0（Ω）=L2（Ω）]，其上的模分别定义为[⋅][k，p]和[⋅][k]；半模为[∣⋅∣k，p]和[∣⋅∣k]；[Tℎ]为[Ω]的矩形剖分，满足正则性条件［13］。对于任意的[K∈Tℎ]，令[ℎK=diamK]，[ℎ=maxK∈TℎℎK]，则非协调[EQrot1]有限元空间[Mℎ]定义为：

[Mℎ={v ; v|K∈span{1， x， y， x2，y2}， ∫F[v]ds=0， ][F⊂∂K， ∀K∈Tℎ}]，这里[[v]]表示跨过单元边界[F]的跳跃度，当[F⊂∂Ω]时，[[v]=v]，容易验证[∣⋅∣ℎ=（∑K∈Tℎ∣⋅∣21，K）12]是[Mℎ]上的模。

定义插值算子 [Πℎ：v∈H1（Ω）→Πℎv∈Mℎ]，满足：

[ΠK=Πℎ|K，∫l（ΠKv−v）ds=0，∀l∈∂K，" ∫K（ΠKv−v）dxdy=0，∀K∈Tℎ]。

方程（1）的变分形式为：求[u∈H10（Ω）]，使得

[（ut，v）+α（∇ut，∇v）+β（∇u，∇v）+（∇⋅u，v）+（u∇⋅u，v）=0u（X，0）=u0（X），∀v∈H10（Ω）" "] （2）

其中，[（u，v）=∫Ωuvdxdy]。

2 半离散格式超收敛分析

本节主要研究半离散格式下的超逼近性质和超收敛分析。首先，给出如下的引理：

引理2.1［10-11］ 对任意的[vℎ∈Mℎ， a（X）∈W1，∞（K）]，有：

[ u−Πℎu0+ℎ[u−Πℎu]ℎ≤Cℎ2u2，u∈H2（Ω）] （3）

[ vℎ0，k≤Cvℎℎ]" （4）

[（∇（u−Πℎu），∇vℎ）ℎ=0] （5）

[（m→⋅∇vℎ， vℎ）ℎ=0] （6）

[（∇⋅（u−Πℎu）， vℎ）ℎ≤Cℎ2u3vℎℎ， u∈H3（Ω）]" （7）

[" " "∑K∈Tℎ∫∂K∂u∂nvℎds≤Cℎ2|u|3vℎℎ，" " "u∈H3（Ω）] （8）

[" " " "|a（X）−a（X）______|0，∞，K≤Cℎa1，∞，K，" " "∀ K∈Tℎ] （9）

其中，[（ϕ，φ）ℎ=∑K∈Tℎ∫Kϕφdxdy]，[m→]为常数向量，[" a（X）_______|K=1|K|∫Ka（X）dxdy]，[C]是一个跟网格尺寸[ℎ]时间均无关的常数。

式（2）对应的非协调半离散格式为：求[uℎ∈Mℎ]，使得：

[（uℎt，vℎ）+α（∇uℎt，∇vℎ）ℎ+β（∇uℎ，∇vℎ）ℎ+（∇⋅uℎ，vℎ）ℎ+（uℎ∇⋅uℎ，vℎ）ℎ=0uℎ（X，0）=Πℎu0（X），" ∀vℎ∈Mℎ] （10）

定理2.1设[u]和[uℎ]分别为式（2）和（10）的解，当[u，ut∈L2（0，T;H3（Ω））]时，有：

[uℎ−Πℎu][ℎ≤Cℎ2]。

证明：令[u−uℎ=（u−Πℎu）+（Πℎu−uℎ）=ξ+η]，由式（2）和（10）可得误差方程：

[（ηt，vℎ）+α（∇ηt，∇vℎ）ℎ+β（∇η，∇vℎ）ℎ+（∇⋅η，vℎ）ℎ=−（ξt，vℎ）−α（∇ξt，∇vℎ）ℎ−β（∇ξ，∇vℎ）ℎ−（∇⋅ξ，vℎ）ℎ+α∑K∫∂K∂ut∂nvℎds+β∑K∫∂K∂u∂nvℎds−（u∇⋅u−uℎ∇⋅uℎ，vℎ）ℎ] （11）

在式（11）中令[vℎ=η]，由式（5）和（6）可得：

[12ddt（η20+αη2ℎ）+βη2ℎ=−（ξt，η）−（∇⋅ξ，η）ℎ+α∑K∫∂K∂ut∂nηds+β∑K∫∂K∂u∂nηds−（u∇⋅u−uℎ∇⋅uℎ，η）ℎ=" " " " " " " " "i=15Ai]（12）

由式（3）、（7）和（8）得到：

[|A1|=|（ξt，η）|≤Cξt0η0≤Cℎ2u2η0≤" " " " " " " " " Cℎ4ut22+Cη20]，

[|A2|=|（∇⋅ξ，η）|≤Cℎ2u3η2ℎ≤Cℎ4u23+" " " " " nbsp; " " " "Cη2ℎ]，

[|A3+A4|=|α∑K∫∂K∂ut∂nηds+β∑K∫∂K∂u∂nηds|≤Cℎ2（u3+ut3）ηℎ≤]

[Cℎ4（u23+ut23）+Cη2ℎ]。

接下来为了估计非线性项[A5]，我们给出如下归纳假设：

对任意的[t∈[0，T]] ，都有" "[uℎ（t）ℎ≤C1] （13）

利用文献［14］中的方法可以证明该假设是成立的。

[|A5|=|（u∇⋅u−uℎ∇⋅uℎ，η）ℎ|=|（（u−uℎ）∇⋅u，η）+" " " " " " " （uℎ∇⋅（u−uℎ），η）|][=|（ξ∇⋅u，η）+（η∇⋅u，η）+" " " " " " " （uℎ∇⋅ξ，η）+（uℎ∇⋅η，η）|] （14）

由式（3）可得[（ξ∇⋅u，η）≤Cℎ2u3ηℎ≤][Cℎ4+η2ℎ]" " " " " " " " " " " " " " " " " " " " " " " " "（15）

[（η∇⋅u，η）≤Cηℎ] （16）

进而，由式（3）、（4）、（7）、（9）和归纳假设（13），可得：

[（uℎ∇⋅ξ，η）=（（uℎ−u）∇⋅ξ，η）+（u∇⋅ξ，η）= （（uℎ−u）∇⋅ξ，η）+（（u−u）∇⋅ξ，η）+（u∇⋅ξ，η）≤]

[ Cuh-u0，4∇⋅ξ0η0，4++Cu-u0，4+ Cu-u0，4∇⋅ξ0η0，4Cu-u0，4∇⋅ξ0η0，4+][ Cℎ2u3ηℎ[≤Cℎ4+Cη2ℎ]" " " " " " " " "（17）

将式（15）—（17）的结果代入式（14），有：

[|A5|≤Cℎ4+Cη2ℎ]。

最终，将上面[A1—A5]的估计结果代入（12），并从[0]到[t]积分，由[η0=0]，并利用Gronwall's 引理［12］可得[ηℎ≤Cℎ2]，结论得证。

接下来，为了得到超收敛结果，我们将相邻的四个单元[K1、K2、K3、K4]合并为一个大单元[K～]，即[K～=i=14Ki]，对应的剖分记为[T2ℎ]。构造如下的插值后处理算子[Π2ℎ]［18-19］：

[ Π2ℎu∣K～∈P2（K～）， ∫Li（Π2ℎu−u）ds=0， i=1，2，3，4，∀ K～∈T2ℎ∫K1⋃K3（Π2ℎu−u）dxdy=0，" ∫K2⋃K4（Π2ℎu−u）dxdy=0]

其中[P2（K～）]表示在[K～]上次数小于等于2的多项式空间，[Li （i=1， 2， 3， 4）]是[K～]的四条边。由文献［18-19］可知[Π2ℎ]满足如下的性质：

[Π2ℎΠℎu=Π2ℎu]，[Π2ℎu−uℎ≤Cℎ2u3]，

[Π2ℎvℎℎ≤Cvnℎ，" " ∀ vℎ∈Mℎ]。

由于[Π2ℎuℎ−u=Π2ℎuℎ−Π2ℎΠℎu+Π2ℎΠℎu−u]，利用三角不等式，我们可以进一步得到如下的超收敛性质：

定理 2.2 设[u∈H3（Ω），]在定理3.1的条件下，有：

[Π2ℎuh−uℎ≤Cℎ2]。

3 向后Euler全离散格式超收敛分析

本节给出向后Euler全离散格式下的超逼近和超收敛分析。

令[{tn=nΔt;n=0，1，2，…，N}]为[[0，T]]的剖分，时间步长为[Δt=T/N]。任给一[[0，T]]上的连续函数[u]，定义[un=u（X，tn），" ∂tun=un−un−1Δt]。

（2）式对应的向后Euler全离散格式为：求[Unℎ∈Mℎ]，使得

[（∂tUnℎ， vℎ）+α（∇∂tUnℎ，∇vℎ）ℎ+β（∇Unℎ，∇vℎ）ℎ+（∇⋅Unℎ， vℎ）ℎ+（Unℎ∇⋅Unℎ， vℎ）ℎ=0，U0ℎ=Πℎu0（X），" " "∀vℎ∈Mℎ" " " " " " " " " ] （18）

类似于半离散情形，我们可得：

[Unℎℎ≤C2， n=1，2，…，N]" " " " " " " " " " " （19）

下面的定理给出了超逼近结果：

定理 3.1 令[un]和[Unℎ]分别为式（2）和（18）的解，" " " " " " " " " " "当 [ u∈L∞（0，T;H3（Ω）） ut∈L2（0，T;H3（Ω））utt∈L2（0，T;H1（Ω））]时，有：

[ Π2ℎun−unhℎ≤C（ℎ2+Δt）]。

证明：令[un−Unℎ=un−Πℎun+Πℎun−Unℎ=ξn+ηn]，则由式（2）和（18）可得误差方程为：

[（∂tηn，vℎ）+α（∇∂tηn，∇vℎ）ℎ+β（∇ηn，∇vℎ）ℎ+（∇⋅ηn，vℎ）ℎ=−（∂tξn，vℎ）−α（∇∂tξn，∇vℎ）ℎ−β（∇ξn，∇vℎ）ℎ+α∑K∫∂K∂unt∂nvℎds+β∑K∫∂K∂un∂nvℎds−（un∇⋅un−Unℎ∇⋅Unℎ，vℎ）ℎ" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " ] （20）

其中[Rn1=unt−∂tun=1Δt∫tntn−1（τ−tn−1）utt（τ）dτ]。

在式（20）中令[vℎ=ηn]，结合式（5）和式（6），有：

[（∂tηn，ηn）+α（∇∂tηn，∇ηn）ℎ+β（∇ηn，∇ηn）ℎ= −（∂tξn，ηn）−（∇⋅ξn，ηn）ℎ−（Rn1，ηn）−α（∇Rn1，∇ηn）ℎ+ α∑K∫∂K∂unt∂nηnds+β∑K∫∂K∂un∂nηnds−（un∇⋅un− Unℎ∇⋅Unℎ，ηn）ℎ=i=17Bi]" " " " " " " " " " " " " " " " " " " " （21）

式（21）左端可估计为：

[（∂tηn，ηn）≥12Δt（ηn20−ηn-120），][" " " " α（∇∂tηn，∇ηn）ℎ≥α2Δt（ηn2ℎ−ηn-12ℎ） ] （22）

下面我们估计式（21）的右端项，由泰勒展开式可知：

[" " " |B3+B4|=|（Rn1，ηn）+α（∇Rn1，∇ηn）]h[|≤]

[ CΔt∫tntn−1utt21dτ+Cηn2ℎ]。

由引理3.1和式（19）可得：

[" " " |B1+B2|=|（∂tξn，ηn）+（∇⋅ξn，ηn）h|][≤][ Cℎ4（1Δt∫tntn−1ut22dτ+un23）+Cηn2ℎ，]

[" " " |B5+B6|=|α∑K∫∂K∂unt∂nηnds+β∑K∫∂K∂un∂nηnds|≤ Cℎ4（unt23+un23）+Cηn2ℎ，]

[|B7|=|（un∇⋅un−Unℎ∇⋅Unℎ，ηn）h|=|（（un−" Unℎ）∇⋅" "un， ηn）+（Unℎ∇⋅（un−Unℎ）， ηn）|ℎ=|（ξn∇⋅un， ηn）+（ηn∇⋅" "un，ηn）+（Unℎ∇⋅ξn，ηn）ℎ+（Unℎ∇⋅ηn，ηn）|][ℎ][≤Cℎ4un23]+

[" Cηn2ℎ。]

将[B1]—[B7]的结果代入式（21）并结合式（22），得：

[12Δt[（ηn20−ηn-120）+α（ηn2ℎ-ηn-12ℎ）]≤Cℎ4（un23+unt23+1Δt∫tntn−1ut22dτ）+" "CΔt∫tntn−1utt21dτ+Cηn2ℎ]。

上式两端同时乘[2Δt]，并从1到[n]求和，同时注意到[η0=0]，有：

[ηn2ℎ≤Cℎ4（Δti=1n（ui23+uit23）+∫tn0ut22dτ）+C（Δt）2∫tn0utt21dτ+CΔti=1nηt21]。

选取足够小的[Δt]使得满足[1−CΔtgt;0，]由离散的 Gronwall's 引理，可得：

[ηn2ℎ≤Cℎ4（u2L∞（0，T;H3（Ω））+ut2L∞（0，T;H3（Ω））+" "∫tn0ut23dτ）+C（Δt）2∫tn0utt21dτ≤C（ℎ4+（Δt）2）]。

结论得证。

最终，在超逼近结果的基础上，可以导出下面的超收敛结果。

定理3.2 在定理3.1的条件下，有如下超收敛结果：

[Π2ℎUnℎ−unℎ≤C（ℎ2+Δt）]。

4 数值例子

本节我们给出相应的数值试验验证理论分析的有效性。

考虑如下的BBMB方程：

[" "ut−Δut−Δu+∇⋅u+u∇⋅u=g（t， X），（X， t）∈Ω×（0，T]u（X， t）=0，" " " " " " " " " " " " " " " " （X， t）∈∂Ω×（0，T]u（X，0）=u0（X），" " " " " " " " " " " " X∈Ω]

其中[Ω=[0，1]×[0，1]，]给出[u]的一个精确解：

[u（x，y，t）=（1+e−t）x2y2（x−1）2（y−1）2]。

前面的理论分析中所讨论的方程（1）的右端项为零，而上面数值例子中方程的右端项为[g（t，X）]，这是为了给出合适的精确解[u（x，y，t）]，从而可以进一步地比较精确解与近似解的误差。

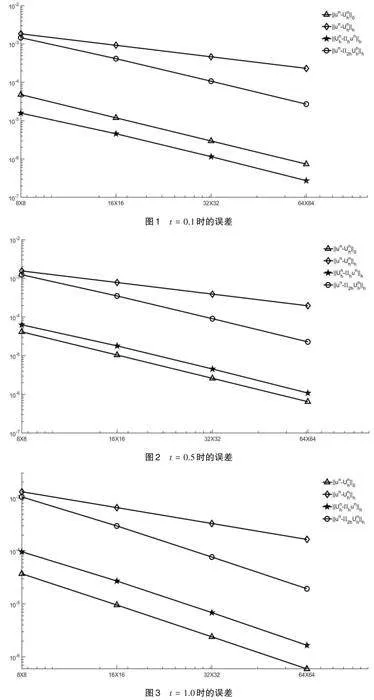
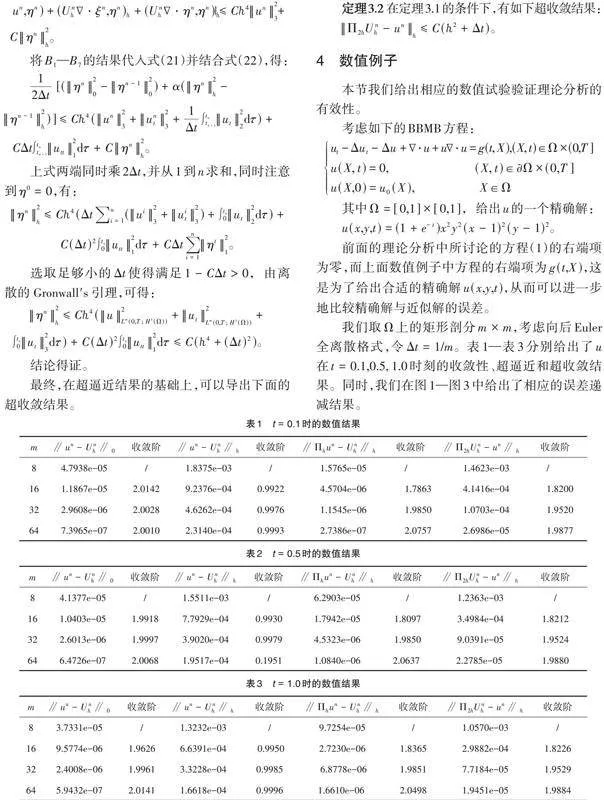
我们取[Ω]上的矩形剖分[m×m]，考虑向后Euler 全离散格式，令[Δt=1/m]。表1—表3分别给出了[u]在[t=0.1，0.5， 1.0]时刻的收敛性、超逼近和超收敛结果。同时，我们在图1—图3中给出了相应的误差递减结果。

从表1—表3和图1—图3可以看出：[un−Unℎℎ]的收敛阶为[O（ℎ）]，[ un−Unℎ0]、[Unℎ−Πℎunℎ]和[ Π2ℎu−uℎ]的收敛阶为[O（ℎ2）]，与我们的理论分析是相吻合的。

参考文献：

［1］DOGAN A.A galerkin finite element approach to Burgers' equation［J］.Applied Mathematics and Computation，2004，157（2）：331-346.

［2］KUTLUAY S，ESEN A，DAG I. Numerical solutions of the Burgers' equation by the least-squares quadratic B-spline finite element method［J］.Journal of Computational and Applied Mathematics，2004，167（1）：21-33.

［3］SHI D Y，YANG H J. A new approach of superconvergence analysis for nonlinear BBM equation on anisotropic meshes［J］. Applied Mathematics Letters，2016，58：74-80.

［4］SHI D Y，JIA X. Superconvergence analysis of two-grid finite element method for nonlinear Benjamin-Bona-Mahony equation［J］.Applied Numerical Mathematics，2020，148：45-60.

［5］OMRANI K，AYADI M. Finite difference discretization of the Benjamin-Bona-Mahony-Burgers equation［J］.Numerical Methods for Partial Differential Equations： An International Journal，2008，24（1）：239-248.

［6］ZAREBNIA M，PARVAZ R. On the numerical treatment and analysis of Benjamin-Bona-Mahony-Burgers equation［J］.Applied Mathematics and Computation，2016，284：79-88.

［7］KARAKOC S B G，BHOWMIK S K. Galerkin finite element solution for Benjamin-Bona-Mahony-Burgers equation with cubic B-splines［J］.Computers Mathematics with Applications，2019，77（7）：1917-1932.

［8］DEHGHAN M，ABBASZADEH M，MOHEBBI A. The use of interpolating element-free Galerkin technique for solving 2D generalized Benjamin-Bona-Mahony-Burgers and regularized long-wave equations on non-rectangular domains with error estimate［J］. Journal of Computational and Applied Mathematics，2015，286： 211-231.

［9］YAN N N. Superconvergence analysis and a posteriori error estimation in finite element methods［M］. Beijing： Science Press，2008.

［10］SHI D Y，LIAO X，WANG L L.Superconvergence analysis of conforming finite element method for nonlinear Schrodinger equation［J］.Applied Mathematics and Computation，2016，289：298-310.

［11］WANG J，LI M，LI X.A new energy-stable nonconforming finite element method for Sobolev equation with Burgers' type nonlinearity［J］.Applied Mathematics Letters，2023，135：108440.

［12］杨怀君.非线性耦合偏微分方程的有限元分析［D］.郑州：郑州大学，2019.

［13］CIARLET P G.The finite element method for elliptic problem［M］.North Holland：Amsterdam，1978.

［14］SHI X Y，Lu L Z.Unconditional superconvergent analysis of quasi-Wilson element for Benjamin-Bona-Mahony equation［J］.Journal of Computational Mathematics，2023，41（1）：94-106.

责任编校：刘 燕，田 旭

Superconvergent Analysis of Nonconforming Finite Element Method for the Nonlinear Benjamin-Bona-Mahony-Burgers Equation

LIAO Xin1，ZHAO Guoying2

（1. School of Mathematics ， Zhengzhou University of Aeronautics ， Zhengzhou 450046 ，China；

2. Unit 32738 of PLA ， Zhengzhou 450046 ， China

Abstract： In this paper，we study the nonconforming finite element method for the Benjamin-Bona-Mahony-Burgers （BBMB for short） equation. By use of the special property of the nonconforming [EQrot1]element ： the consistency error is one order higher than its interpolation error，the superclose and superconcergence results in semi-discrete and" Euler full discrete schemes are obtained for this equation. Finally，a numerical example is provided to illustrate validity and efficiency of our theoretical analysis and method.

Key words： nonlinear BBMB equation; nonconforming [EQrot1]element; semi-discrete scheme; euler full discrete scheme; superclose and superconcergence

基金项目：河南省科技攻关项目（222102210228）

作者简介：廖 歆，男，河南许昌人，博士，研究方向为有限元方法。