带有时滞和收获的扩散捕食系统的斑图动力学分析

摘 要：文章研究了一类带有食饵收获效应和时滞的捕食系统的Turing斑图的形成及选择问题。首先利用稳定性理论给出了由交叉扩散项引起的Turing不稳定条件和分支理论分析，得到了系统Turing斑图的存在区域。然后利用Matlab软件对系统Turing斑图的形成和选择结果进行了数值模拟。这为以后带有交叉扩散的时滞反应扩散系统的研究提供了可行的方法，具有广泛的理论应用价值。

关键词：捕食系统；扩散；时滞；收获；图灵分支

中图分类号：O175.21" "文献标识码：A" " 文章编号：1007 - 9734 （2024） 02 - 0108 - 05

0 引 言

时空斑图是由图灵首次提出的一种在时间或空间上具有某种规律性的非均匀宏观结构［1］。它在自然界中普遍存在，如天上的云彩、动物表皮的纹路、化学反应的图案等，故研究斑图的形成和选择机制有利于认识自然、解开自然之谜［2］。文献［3］主要考虑了一个具有Holling II型捕食者功能响应的扩散捕食系统，该系统受到诺伊曼边界条件的影响，但作者仅通过自扩散来处理个体的随机运动，即

[∂u∂t=d1∇2u+u（1-uK）-uva+u∂v∂t=d2∇2v+v（bua+u-c）∂u∂n=∂v∂n=0] （1）

其中[u， v]分别表示空间位置[（x，y）∈Ω]在时刻[t]时的被捕食者和捕食者的密度；[∇2=∂∂x2+∂∂y2]表示二维空间区域[Ω]上的拉普拉斯算子；[∂u∂n=∂v∂n=0]表示没有种群穿越边界；[n]表示区域边界[∂Ω]的单位外法向量；[d1， d2]表示被捕食者和捕食者的正自扩散系数；[K， a， c]分别表示被捕食者的环境容纳量，捕食者对食饵的最大摄入比率及捕食者的自然死亡率。然而，该系统忽略了至少如下三个重要问题： 一是系统（1）仅考虑了自扩散现象，但捕食者和被捕食者之间的交叉扩散也是自然界中十分常见的现象［4-6］，需要进行考虑；二是在捕食系统中，收获对系统的动力学行为有重要影响，会破坏系统的稳定性并产生周期解、极限环等现象［7-8］， 因此，需要考虑被捕食者的收获现象；三是捕食者猎杀被捕食者后转化成自身的生长，以及物种的妊娠期都不是瞬时完成的，因此，物种的密度不仅依赖当前时刻，也会依赖过去时刻物种的浓度，这就需要引入时滞［9-13］。为解决如上问题，本文主要研究如下系统（2）：[∂u∂t=d1∇2u+d12∇2（uv）+u1-u（t-τ）K-uva+u-h∂v∂t=d21∇2（uv）+d2∇2v+vbu（t-τ）a+u（t-τ）-c∂u∂n=∂v∂n=0]

其中[d12， d21]表示物种之间的相互作用扩散系数； [h]表示被捕食者的线性收获；[τ]表示常数时滞。

1 主要结果

1.1" 系统（2）对应的常微分系统稳定性分析

考虑系统（2）所对应的常微分系统：

[∂u∂t=u1-uK-uva+u-h∂v∂t=vbua+u-c] （3）

考虑到生态学意义，本文只研究系统（2）和（3）的正平衡点。通过求解，易知当[bgt;c，" 0lt;hlt;h0][h0=ac（Kb-Kc-ac）K（b-c）2]时，系统（2）和（3）存在唯一的正平衡点[E*=（u*，v*）=acb-c，abc（Kb-Kc-ac）-Kb（b-c）2hKc（b-c）2]。

接下来研究系统（3）在平衡点[E*]处的稳定性。

通过简单的计算，我们可以得出系统（3）在平衡点[E*]处的稳定性情况如下：

定理1 假设[bgt;c， 0lt;hlt;h0]成立，令

[h*=-ac2（Kb-Kc-ab-ac）K（b-c）3。]若[0lt;hlt;h*，]则[E*]是局部渐进稳定的；若[hgt;h*，]则[E*]是不稳定的；若[h=h*，]则系统在平衡点[E*]处发生Hopf分支。

取[K=3.6， a=1.8， b=3.2， c=1.5]，则[h0=0.8875432526， h*=0.5358233259]。令[h=0.06]，系统的共存平衡点为[E*=（1.588235294，1.765425606）]，它是局部渐进稳定的，如图1（a）所示。 取[h=0.545，]系统的共存平衡点[E*]失去它的稳定性，周围出现一个稳定的极限环，如图1（b）所示。

1.2" 系统（3）特征方程的推导

令 [" " "u（x，y，t-τ）≈u（x，y，t）-τ∂u（x，y，t）∂tF（u，u（t-τ），v）≜u1-u（t-τ）K-uva+u-hG（u，u（t-τ），v）≜vbu（t-τ）a+u（t-τ）-c]，

在[τ=0]附近对[F（u，u（t-τ），v）]和[G（u，u（t-τ），v）]泰勒展开得

[" "F（u，u（t-τ），v）=F（u，v）-τ∂F∂u（t-τ）⋅∂u∂tτ=0，]

[" "G（u，u（t-τ），v）=G（u，v）-τ∂G∂u（t-τ）⋅∂u∂tτ=0，]

其中， [F（u，v）=F（u，u（t-τ），v）τ=0=u1-uK-uva+u-h，][G（u，v）=G（u，u（t-τ），v）τ=0=]

[vbua+u-c]。

所以，系统（2）可转化成如下系统

[p1∂u∂t=d1∇2u+d12∇2（uv）+F（u，v）p2∂u∂t+∂v∂t=d21∇2（uv）+d2∇2v+G（u，v）] （4）

其中，[p1=1+τ∂F∂u（t-τ）τ=0=1-τu*K，]

[p2=τ∂G∂u（t-τ）τ=0=τabv*（a+u*）2。]

定义[D=d1+d12v*d12u*d21v*d2+d21u*，M=p10p21，]

[J=∂F∂u∂F∂v∂G∂u∂G∂vE*=m11m12m210，]其中

[" " " m11=K（b-c）3h+ac2（Kb-Kc-ac）（b-c）Kabc，m12=-cblt;0，" m21=ac（Kb-Kc-ac）-K（b-c）2hKacgt;0]。

令[λM+k2D-J=0]，我们可得系统（2）的特征方程为

[λ2+g（k2）λ+h（k2）=0]" （5）

其中，

[g（k2）=1p1（u*d21p1-u*d12p2+v*d12+d2p1+d1）k2+p2m12-m11，h（k2）=1p1（u*d1d21+v*d2d12+d1d2）k4+（u*d12m21-u*d21m11+v*d21m12-d2m11）k2-m12m21]" " " "特征方程（5）的根为

[" " " "λk=12-g（k2）±g（k2）2-4h（k2）]。

1.3" Turing分支

我们选择[h]作为分支参数，如果当[k=0]时，[Im（λk）≠0， Re（λk）=0，]则系统（2）将会发生Hopf分支，因此我们可获得收获的临界值为

[hc=ac2（b-c）（Kb-Kc-ac）τ+Kb-Kc-ab-acK（b-c）3（cτ-1）]。

如果当[k=kc≠0]时，[Im（λk）=0， Re（λk）=0，]则系统（2）将会发生Turing分支。假设时滞[τ]很小，则[p1=1-τu*Kgt;0] 。因此，Turing分支发生的具体条件如下：

l当[k=0]时，系统（2）在平衡点[E*]处是稳定的，即

[g（0）=m2m12-m11p1gt;0，h（0）=-m12m21p1gt;0]。

从[g（0）gt;0]可得[hlt;hc]，而[h（0）gt;0]总是成立的。

l当[k≠0]，我们考虑由[h（k2）lt;0]造成的Turing失稳。具体地，系统（2）应满足如下两个条件：

（C1）[（u*d12m21-u*d21m11+v*d21m12-d2m11）2+4m12m21（u*d1d21+v*d2d12+d1d2）gt;0， p1gt;0，]

（C2）[u*d12m21-u*d21m11+v*d21m12-d2m11lt;0]。

条件（C1）保障了Turing分支的存在性；条件（C2）确保[h（k2）]的最小值小于零。因此我们可以获得系统（2）的临界波数[k2c=-u*d12m21-u*d+21m11+v*d+21m12-d2m112（u*d1d+21+v*d2d12+d1d2）]，其中Turing分支参数[d21]的临界值为

[d+21=h1+m12m21（v*d12m12-u*d12m11+d1m12）（u*2d1m21-v*2d2m12+u*v*d2m11）（u*m11-v*m12）2]，

其中，[h1=u*2d12m11m21-u*v*d12m12m21-2u*d1m12m21-u*d2m211+v*d2m11m12]。

总结以上讨论，我们可得系统（2）发生如下丰富的斑图动力学行为：

定理2 假设[0lt;hlt;h*]，[hlt;h0]，[bgt;c]成立。 则

l当[h=hc]时，系统（2）在[E*]处发生Hopf分支。

l当[hlt;hc]，且条件（C1）、（C2）成立时，系统（2）在[E*]处发生Turing分支。 扩散诱发的分支点是[d21=d+21]，此时临界波数为[k2=k2c]，即Turing空间为

[h， d210lt;hlt;hc， d21gt;d+21]。

l当[hgt;hc]时，系统（2）在平衡点[E*]处是不稳定的。

2 数值仿真

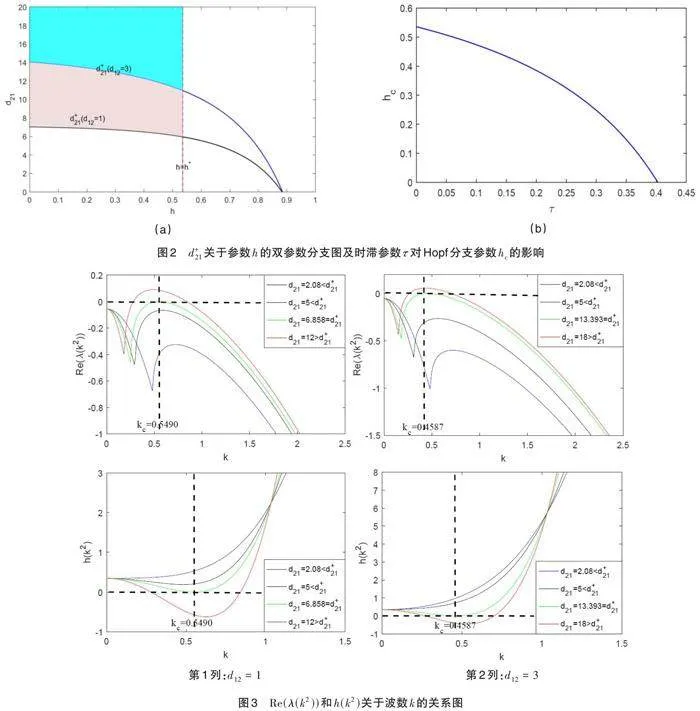
取[K=3.6， a=1.8， b=3.2， c=1.5， d1=0.3， d2=0.3， τ=0.01]，图2（a）展示了参数[d21]在[d12]分别取值1和3时随[h]变化的情况。从定理2可知，图2（a）中的阴影部分就是Turing参数空间，我们发现随着参数[d12]的增大，Turing参数空间减小，这就意味着，与[d21]相比，交叉扩散系数[d12]抑制Turing斑图的形成。

图2（b）描述了时滞参数[τ]对Hopf分支参数[hc]的影响，发现随着[τ]的增加，[hc]不断减小，从而Turing空间将不断缩小，说明系统的时滞会抑制Turing分支的发生。

图3用来描述Turing失稳的条件。固定[h=0.2lt;hc=0.5304671847]，其他参数的取值和前文一致。从图3可以看出不稳定模和波数随着交叉扩散系数[d21]的增大而增大。具体地，当[d21lt;d+21] 时，特征值的最大实部是负的，这意味着系统处于稳定状态，交叉扩散未诱发Turing分支；当[d21gt;d+21] 时，对于适当的波数，特征值的最大实部是正的，这意味着系统处于不稳定状态，交叉扩散诱发了Turing分支。

3 结 论

本文研究了一类带有收获和时滞的反应扩散系统，得到了系统在其正平衡点处发生Turing分支的存在条件和Turing空间。通过数值模拟发现，交叉扩散系数[d12]和时滞[τ]抑制Turing斑图的形成，而[d21]促进Turing斑图的形成。因此，交叉扩散和时滞对系统的动力学行为均具有重要影响。

参考文献：

［1］TURING A.The chemical basis of morphogenesis［J］. Philosophical Transactions of the Royal Society of London Series B，1952，237：37-72.

［2］JI Y S ，SHEN J W，MAO X C.Pattern formation of brusselator in the reaction-diffusion system［J］.Discrete and Continuous Dynamical Systems-Series S， 2022， in Press.

［3］YI F，WEI J J， SHI J.Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system［J］.Journal of Differential Equations，2008，246：1944-1977.

［4］SIVASAMY R，SIVAKUMAR M，BALACHANDRAN K， et al.Spatial pattern of ratio-dependent predator-prey model with prey harvesting and cross-diffusion［J］. International Journal of Bifurcation and Chaos，2019，29（3）：16.

［5］SONG M R， GAO S P， LIU C. Cross-diffusion induced Turing patterns on multiplex networks of a predator-prey model［J］. Chaos Solitons amp; Fractals， 2023， 168： 113131.

［6］YANG J G， ZHANG T H， YUAN S L. Turing pattern induced by cross-diffusion in a predator-prey model with pack predation-herd behavior［J］.International Journal of Bifurcation and Chaos，2020，30（7）：2050103.

［7］JIAO J F，WANG R Q，CHANG H C，et al. Codimension bifurcation analysis of a modified Leslie-Gower predator-prey model with two delays［J］.International Journal of Bifurcation and Chaos，2018，28（5）：1850060.

［8］刘霞，焦建锋.具有年龄结构的捕食被捕食系统的Bogdanov-Takens分支［J］. 华东师范大学学报（自然科学版），2016（3）：39-47.

［9］焦建锋，陈灿.具双Allee效应的时滞捕食系统的余维3分支分析［J］.华东师范大学学报（自然科学版），2022（2）： 24-33.

［10］JIAO J F，CHEN C.Bogdanov-Takens bifurcation analysis of a delayed predator-prey system with double Allee effect

［J］. Nonlinear Dynamics，2021，104（2）：1697-1707.

［11］LIU X，LIU Y W，WANG J L. Bogdanov-Takens bifurcation of a delayed ratio-dependent Holling-Tanner predator prey system［J］.Abstract and Applied Analysis，2013，2013（54）：1-13.

［12］SONG Y，SHI Q.Stability and bifurcation analysis in a diffusive predator-prey model with delay and spatial average［J］. Mathematical Methods in the Applied Sciences， 2022，46（5）：5561-5584.

［13］于智博，吕堂红，周林华.具有避难所和双时滞的捕食系统的Hopf分支［J］.陕西理工大学学报（自然科学版）， 2022，38（6）：60-69.

责任编校：刘 燕，田 旭

Spatical Dynamics of a Diffusive Prey-Predator Model with Delay and Prey Harvesting

CHANG Hongcui1，JIAO Jianfeng2，WANG Zhanwei2，ZHANG Litao2

（1. College of Economics ， Zhengzhou University of Aeronautics ， Zhengzhou" 450046 ， China；

2. College of Mathematics ， Zhengzhou University of Aeronautics ， Zhengzhou" 450046 ， China）

Abstract： This paper studies the formation and selection of Turing pattern for a class of prey-predator systems with prey harvesting effect and time delay. Firstly， the Turing instability condition induced by the cross-diffusion terms is given by using the stability theory， and the existence region of the Turing pattern of the system is obtained by bifurcation theory. Then， Matlab software is used to simulate the formation and selection results of the Turing pattern of the system. This provides a feasible method for the study of time-delayed reaction-diffusion systems with cross-diffusion in the future， and has an important theoretical application value.

Key words： prey-predator model；diffusion；delay；harvesting; turing bifurcation

基金项目：国家自然科学基金（12201163）；河南省高校重点科研项目计划基础研究专项（24ZX008）；浙江省自然科学基金（LQ23A010016）

作者简介：常红翠，女，河南卫辉人，助教，研究方向为动力系统的定性与稳定性理论。

∗通讯作者：焦建锋，男，河南洛阳人，讲师，博士，研究方向为生物数学。