未知环境下GNSS辅助视觉自主定位方法

摘 要：自主导航与定位是无人系统智能化的基础，未知环境下持续、稳定、可靠的位置服务对自主导航与定位尤为重要。针对低置信度下GNSS信号微弱、突防能力差、易受干扰而无法持续定位的问题，文章提出了一种GNSS辅助视觉自主动态定位方法，可以在未知环境下提供全局定位服务。该方法以三帧影像及其对应的GNSS坐标作为约束数据，通过Horn坐标变换得到GNSS坐标系和世界坐标系转换矩阵；通过对极几何、单应变换、2D-3D位姿解算，得到后续影像序列在世界坐标系的相对位姿；最终得到GNSS不可用时无人载体在GNSS坐标系的全局位置数据。数据集验证表明，该算法适用于GNSS信号间歇性存在的情况，可以提供全局位置服务，且短时定位精度较高。进一步对比传统状态估计和BA优化后误差，结果表明，相比于传统状态估计，BA优化后定位精度提高10%—20%，证明了在未知环境下该算法具有良好的可靠性和适用性。

关键词：视觉定位；GNSS辅助定位；BA优化；Horn坐标变换

中图分类号：V279;TP391.41" " " " "文献标识码：A" " "文章编号：1007 - 9734 （2024） 02 - 0065 - 07

0 引 言

卫星导航定位系统的发展改变了人们的生活方式、部队的战场感知方式以及政府的交通管理样式等，促进了科学技术、经济和社会的发展［1-2］。但同时，卫星导航定位系统也存在着信号弱、突防能力差、易受干扰等天然脆弱性。在一些复杂的环境中，如城市峡谷、隧道或强干扰的战场，GNSS信号被削弱甚至拒止，此时GNSS接收机获得的位置信息不再可用，需要依靠其他导航方式获得可靠的全球位置坐标。

视觉导航与定位是一种被动、可靠的定位模式，它可以在获取视频或图像序列后，在定位环境中实现自主导航与定位，且具有抗干扰性能强、精度高、成本低等优点，因此在自主智能领域得到了广泛的应用。但视觉定位获得的状态估计位置是相对的，难以确定载体的全局位置，视觉导航误差长期定位存在漂移现象［3］。

GNSS和视觉这两种导航定位方法各有优缺点，可以形成优势互补［4-5］。GNSS可以抑制视觉导航误差的快速积累，而在GNSS受到遮挡和干扰的情况下，视觉导航可以实现连续导航，提高了GNSS导航定位的连续性和精度。

有关GNSS和视觉在松散组合导航定位中的应用的研究较多。Agrawal和Konolige［6］首先提出了一种GNSS/VO松散组合系统，使用配备GNSS接收机和双目摄像机的小车进行实验，并证实了GNSS/VO松散组合系统的性能优于纯视觉VO系统。Aumayer等［7］研究了双目视觉辅助GNSS在恶劣环境下的连续导航性能，将纯视觉导航结果与GNSS结果松散地结合在一起。实验表明，在微弱GNSS环境下，当GNSS精度降低到10m时，视觉导航结果的精度优于1m，因此视觉导航系统可以很好地辅助GNSS进行连续导航。

此外，Schreiber等［8］采用GNSS/惯性紧密结合系统，利用伪测距或载波相位原始观测，最终实验证明，当卫星数量低于4颗时，仍然可以进行紧密结合定位解决方案。王磊等［9］提出将已知世界坐标系下图像中的特征点作为“视觉伪卫星”，与GNSS测距信号紧密结合，实现弱GNSS环境下的连续导航。文献［10-11］利用卫星观测不足情况下的紧密结合，开展了GNSS与视觉结合的导航研究。

综上所述，关于视觉与GNSS结合辅助的研究较多。然而，这些研究大多基于视觉/GNSS松散耦合或紧密耦合的通用框架，需要GNSS信号长时间存在才能用于导航和定位，不适用于GNSS拒绝可用或仅存在机会性信号的情况。针对上述问题，本文利用间歇性可用的GNSS位置坐标作为约束数据辅助视觉进行定位，实现在GNSS数据不可用情况下仍可获得无人载体的全局位置服务。最后，通过数据集对本文算法进行测试，验证其适用性和可靠性。

1 GNSS辅助下视觉动态定位模型

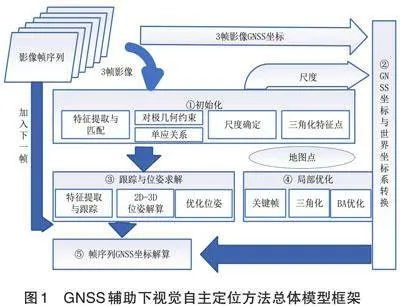
以三帧影像以及其对应的GNSS坐标为约束数据，通过Horn坐标变换［12］，计算得到GNSS坐标系和世界坐标系（第一帧影像的相机坐标系作为世界坐标系）转换矩阵；通过对极几何［13］、单应变换［13］、2D-3D位姿解算，得到后续影像序列在世界坐标系的相对位姿；通过GNSS坐标系和世界坐标系转换矩阵，最终得到GNSS不可用时载体在GNSS坐标系的位置数据。方法总体框架如图1所示，包括初始化，GNSS和世界坐标系转换，跟踪和位姿求解，局部优化，帧序列GNSS坐标解算五部分。

1.1" 初始化

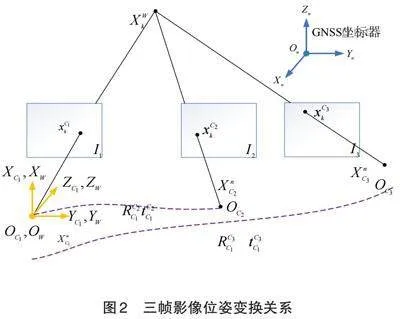
如图2所示，[I1]、[I2]、[I3]为有GNSS定位数据的三帧影像，对应的相机光心位置为[C1]、[C2]、[C3]，GNSS坐标为[XnC1]、[XnC2]、[XnC3]。在此，假定[C1]处相机坐标系[OC1XC1YC1ZC1]为世界坐标系[OWXWYWZW]。

（1）对极约束位姿求解

对[I1]、[I2]、[I3]进行orb特征点提取与匹配，得到m个匹配同名点，以第k个同名点为例，记在[I1]、[I2]、[I3]中像素归一化坐标为[xC1k]、[xC2k]、[xC3k]。

根据对极几何，建立以下约束条件，如公式（1）：

[xC2kTEC2C1xC1k=0，EC1C2=KTFC1C2K= [tC1C2]×RC1C2] （1）

其中，[EC1C2]表示[I1]到[I2]的本质矩阵，[FC1C2]表示[I1]到[I2]的基本矩阵，[RC1C2]表示[C1]运动到[C2]的旋转矩阵，[tC1C2]表示[C1]运动到[C2]的平移向量。

对[EC1C2]本质矩阵进行SVD分解，得到四种组合对应的[RC1C2]、[tC1C2]，通常把任意一点代入，判断该点的深度，利用特征点需在相机前这一约束条件，选择唯一正确的位姿解算结果[RC1C2]、[tC1C2]。

（2）单应矩阵位姿求解

如果同名点在同一平面上，可以根据单应关系进行位姿解算，如公式（2）：

[xC2k=HC2C1xC1k] （2）

其中，[HC2C1]表示[I1]到[I2]的单应矩阵。

对单应矩阵[HC2C1]进行SVD分解，如下公式（3）：

[HC2C1=UDVT，D=RD+tDnDTd] （3）

其中，[U]、[V]为正交矩阵，[D]为对角阵。

以[D]为新的单应矩阵，进行SVD分解，可以得到单应关系下的[RC1C2]、[tC1C2]：

[RC1C2=URDVTn=VnDtC1C2=dUtD] （4）

（3）模型评分

以上对对极几何约束和单应关系位姿解算分别进行了介绍。在实际场景中，需要根据拍摄场景特征点分布情况，判断选择哪种模型进行位姿求解。

在此，我们通过判断内点数目进行模型评分，定义比率[ratio]见公式（5），[scoreH]和[scoreF]分别代表[H]矩阵和[F]矩阵评分。

[ratio = scoreHscoreH + scoreF] （5）

在此，根据大量实验结果，设定[ratio]阈值为0.6，当[ratio]大于0.6时，选择单应矩阵进行求解。

（4）尺度确定

以上虽然得到平移向量[tC1C2]，但[tC1C2]为失去尺度的平移向量。根据欧式变换保距性，[C1]运动到[C2]在GNSS坐标系的基线长度和[C1]运动到[C2]的平移向量的欧式距离相等，根据公式（6）可以计算得到尺度因子[λ1，2]。

[tC1C2=λ2，1XnC2-XnC1] （6）

真实平移向量[tC1C2]为：

[tC1C2=tC1C2/λ2，1] （7）

（5）三角化特征点

已知两幅影像同名匹配点和相机矩阵，即可求解同名点的三维坐标。在此，以[C1]为基准坐标系，则[I1]、[I2]对应的相机矩阵为：

[P1=K[I0]P2=K[RC1C2tC1C2]] （8）

代入公式（9）求解可得到第k个特征点对应的世界坐标系下三维坐标[XWk]。

[xC1k=P1XWkxC2k=P2XWk] （9）

通过SVD求解齐次方程组，即可得到三维坐标[XWk]的最小二乘解。

1.2" GNSS坐标系和世界坐标系转换

根据Horn绝对坐标变换，只要有三个不共线的坐标点，便可求解出两个笛卡尔坐标系之间的旋转和平移变换参数。

同理，根据公式（6）、公式（7）可以得到[C1]运动到[C3]的真实尺度下平移向量为：

[tC1C3=tC1C3/λ3，1] （10）

GNSS坐标系和世界坐标系均为刚体坐标系，因此转换矩阵包括旋转向量[RnW]和平移向量[tnW]两部分，在此，已知[C1]在GNSS坐标系的位置[XnC1]即为平移向量[tnW]，[C2]和[C3]在GNSS坐标系的位置为[XnC2]和[XnC3]，即可联合得到关系式（11）。

[XnC2=RnWtWC2+tnWXnC3=RnWtWC3+tnW] （11）

另外，旋转矩阵[RnW]为3*3的正交矩阵，满足以下约束：

[RnW1T=1][RnW2T=1][RnW3T=1] （12）

其中，[RnW1T]、[RnW2T]、[RnW3T]分别表示[RnW]的第1、2、3列向量。

联立公式（11）和公式（12），即可计算得到旋转向量[RnW]。注意，在此起算的三帧影像需要求有足够的空间距离，否则会导致转换矩阵病态。

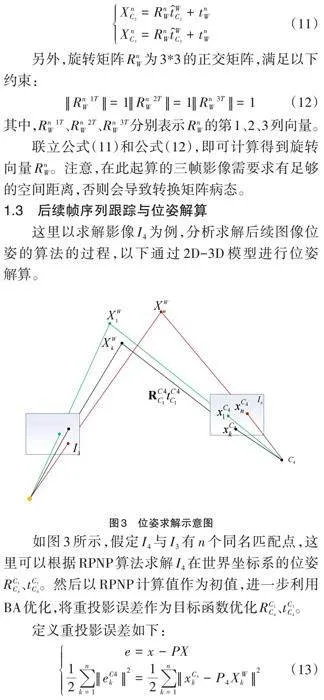
1.3 后续帧序列跟踪与位姿解算

这里以求解影像[I4]为例，分析求解后续图像位姿的算法的过程，以下通过2D-3D模型进行位姿解算。

如图3所示，假定[I4]与[I3]有n个同名匹配点，这里可以根据RPNP算法求解[I4]在世界坐标系的位姿[RC1C4]、[tC1C4]。然后以RPNP计算值作为初值，进一步利用BA优化，将重投影误差作为目标函数优化[RC1C4]、[tC1C4]。

定义重投影误差如下：

[e=x-PX12k=1neC4k2=12k=1nxC4k-P4XWk2 ] （13）

利用重投影误差进行BA优化，选取[P4]最优解。对于每一帧影像，通过匹配当前帧中的特征和上一帧中的特征来估计相机姿态，并通过BA优化估计的相机姿态。

1.4" 局部优化与GNSS坐标求解

如果当前帧被确定为关键帧，则使用该帧创建新的3d地图点。此阶段，通过约束最小化重投影误差调整相机位姿和三维地图点。

假设第i帧相机位姿[RC1Ci]和[tC1Ci]，对应的相机矩阵[Pi]，局部地图中一共有m帧影像。第i帧对应的n个地图点为[XW1，…，XWn]，重投影误差如下：

[e=x-PX12i=1mj=1neij2=12i=1mj=1nxij-PiXWj2] （14）

BA优化的过程即对公式（14）进行最小二乘求解，得到相机位姿和对应地图点的最优解。

当得到后续影像在世界坐标系位姿后，与GNSS和世界坐标系转换矩阵联合求解，即可得到后续帧序列GNSS坐标。结合1.2节和1.3节内容，以下仍以[I4]为例，求解[C4]在GNSS坐标位置如下式：

[XnC4=XnC1+RnWtC1C4] （15）

1.5" GNSS辅助下视觉动态定位算法流程

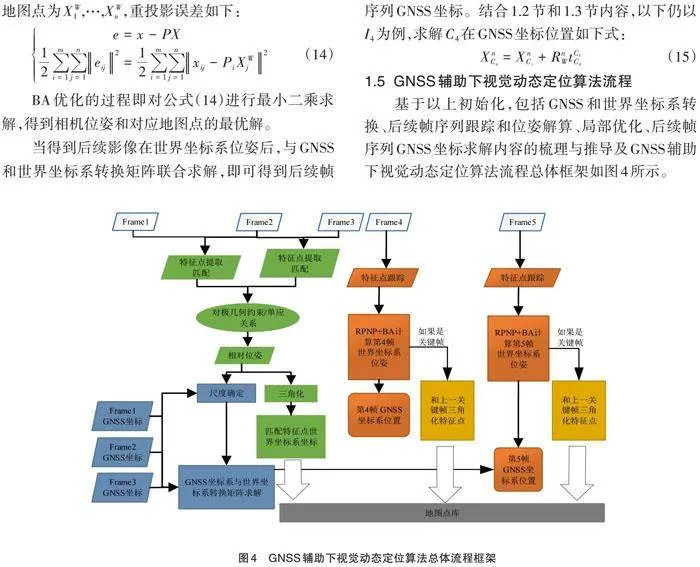
基于以上初始化，包括GNSS和世界坐标系转换、后续帧序列跟踪和位姿解算、局部优化、后续帧序列GNSS坐标求解内容的梳理与推导及GNSS辅助下视觉动态定位算法流程总体框架如图4所示。

GNSS辅助下视觉动态定位算法实施步骤如下：

步骤1：以已知的三帧为初始约束，将Frame1的相机坐标系作为世界坐标系；

步骤2：对Frame1、Frame2进行特征点提取与匹配，对Frame1、Frame3进行特征点提取与匹配；

步骤3：对对极几何约束和单应关系模型进行评估，选择不同模型进行相对位姿估计，得到[RC1C2]、[tC1C2]、[RC1C3]、[tC1C3]；

步骤4：以Frame1、Frame2、Frame3的GNSS位置坐标[XnC1]、[XnC2]、[XnC3]为起算数据，结合[tC1C2]、[tC1C3]计算尺度；

步骤5：利用[RC1C2]、[tC1C2]、[RC1C3]、[tC1C3]、[K]进行特征点三角化，得到前三帧匹配特征点在世界坐标系下的坐标，并放入地图点库；

步骤6：利用已知三帧在GNSS的位置坐标[XnC1]、[XnC2]、[XnC3]和[RC1C2]、[tC1C2]、[RC1C3]、[tC1C3]，计算得到GNSS坐标系和世界坐标系之间的转换矩阵[RnW]、[tnW]；

步骤7：对Frame4进行特征点提取，并与前一关键帧进行特征匹配，利用RPNP求解位姿，并进行BA优化。以Frame4为例，得到其在世界坐标系下的位姿[RC1C4]、[tC1C4]；

步骤8：判断Frame4是否为关键帧，如果为关键帧，与上一关键帧三角化特征点，并将重建后得到的

新的特征点加入地图库。进行BA优化，优化关键帧位姿和地图点位置坐标；

步骤9：利用Frame1的GNSS坐标[XnC1]和步骤6得到的[RnW]、[tnW]，计算Frame4在GNSS坐标系下的坐标；

步骤10：参考步骤7、步骤8和步骤9，依次得到后续帧在GNSS坐标系下的坐标。

2 数据集验证

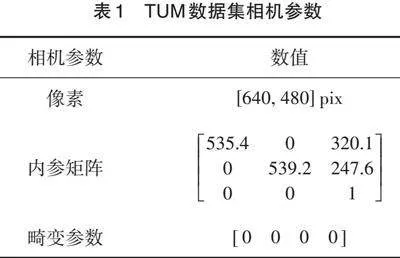
为了验证本文算法，这里采用TUM数据集进行实验，TUM数据集是Ludwig Maximilian大学计算机视觉组采集的室内和室外图像数据集，数据集包含标定文件、5种类型数据以及动作捕捉系统采集的相机真实轨迹。本实验以动作捕捉系统的真值作为GNSS数据，来验证本文提出的模拟GNSS辅助下视觉动态定位方法。TUM数据集相机参数如表 1所示。

2.1 数据处理与分析

（1）第一、二、三帧特征提取与匹配

在此采用三视图序列，对第一、二、三帧提取的orb特征点，设置8层图像金字塔上提取FAST角点，金字塔尺度因子为1.2。orb特征描述子对第一、二帧特征点匹配，共计253对匹配点；第一、三帧匹配，共计得到211对特征点，如图 5和图 6所示。

（2）第一、二、三帧三角化

对第一、二帧和第一、三帧分别三角化，得到对应的地图点，过程包括对极几何F矩阵求解、单应关系H矩阵求解、模型选择、相对位姿求解、尺度确定，数据处理结果如表 2所示。

[tC1C2=-0.98540.1196-0.1213] [RC1C3=0.99240.05210.1114-0.05070.99860.01510.1121-0.00930.9937]

[tC1C3=-0.99570.09200.0114] 真实平移 [λ2，1=9.8177]

[tC1C2=-0.10040.0122-0.0124] [λ3，1=6.9966]

[tC1C3=-0.16440.00599-0.0024] ]

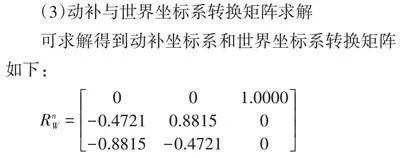
（3）动补与世界坐标系转换矩阵求解

可求解得到动补坐标系和世界坐标系转换矩阵如下：

[RnW=001.0000-0.47210.88150-0.8815-0.47210]

（4）后续相机位姿

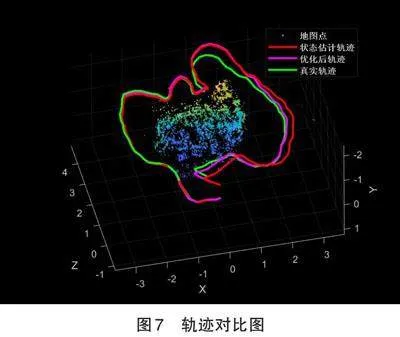
对于后续帧，经过跟踪和局部优化，依次得到对应相机位姿在动补坐标系中的位置和姿态，在此分别对两种算法进行定位，如图7所示。红色米号表示后续帧位姿估计结果，蓝色圆圈表示优化后帧位姿结果，绿色星号表示帧真实位姿数据。

从图7中可以看出，起始阶段，状态估计轨迹、优化轨迹和真实轨迹几乎一致，证明了本文所提出方法的有效性。但是，随着时间的推移，状态估计轨迹和优化轨迹相对于真实轨迹，均出现了明显的漂移现象，这是因为虽然进行了BA优化，但是由于全局位置约束仅在开始有效，后续由于视觉里程计本身的误差积累，导致整体出现了精度下降问题。

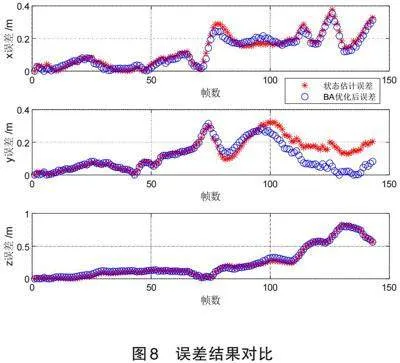
2.2" 误差统计与分析

对状态估计轨迹、优化轨迹相对于真实轨迹进行绝对误差分析，如图8所示。红色米号表示状态估计误差，蓝色圆圈表示BA优化后误差，总体来说，ｘ，ｙ，z三轴误差随着帧数的增加，都出现增大现象；但是，优化后的轨迹误差相对于状态估计误差，有下降趋势。

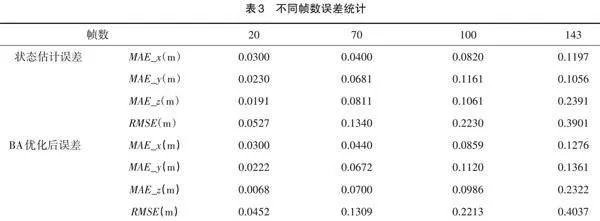
为了分析本文提出的GNSS辅助下视觉动态定位方法的适用性，在此对状态估计误差精度及优化后误差精度进行统计分析。以下对不同帧数（20，70，100，143）平均绝对误差精度进行统计，如表 3所示。

从表3中可以看出，BA优化后误差相对于状态估计误差，有一定的精度提升。从第4帧到20帧进而到70帧，平均绝对误差和均方根误差虽有增加，但是总体误差增长较慢；70帧以后，特别是100帧以后，误差呈现倍速增长。虽然随着时间推移，状态估计误差和BA优化后误差均逐渐变大，但是总体来看，相比于状态估计结果，BA优化后，平均绝对误差减小20%，均方根误差减小20%，最大误差减小了9%。

3 结 论

自主导航是实现无人载体环境感知、自主控制和导航定位等智能化水平的核心技术，是无人系统智能化的基础。未知环境下，依靠间歇GNSS位置辅助视觉动态定位可以为无人载体提供可靠、连续的全局位置服务。本文以三帧影像以及其对应的GNSS坐标为约束数据，研究了未知环境下GNSS辅助视觉动态定位方法。主要的创新之处在于：本文算法仅需要三帧影像GNSS坐标，即可进行全局位置服务。经过数据集实验验证，主要结论如下：

（1）起始阶段，状态估计轨迹、优化轨迹和真实轨迹几乎一致，证明了本文所提出方法的有效性。但是，随着时间的推移，状态估计轨迹和优化轨迹相对于真实轨迹，均出现了明显的漂移现象，这是因为虽然进行了BA优化，但是由于全局位置约束仅在开始有效，后续由于视觉里程计本身的误差积累，而导致整体精度下降。

（2）虽然随着时间推移，状态估计误差和BA优化后误差均逐渐变大，但是相比于状态估计结果，BA优化后，平均绝对误差减小20%，均方根误差减小20%，最大误差减小9%。

综上，本文所提出的算法能够提供连续、稳定、鲁棒的位置服务。且BA优化后结果相比于原有状态估计结果，定位精度有所提升。下一步考虑引入GNSS数据或者其他数据进行约束，抑制随时间推移误差增大的现象。

参考文献：

［1］杨元喜.综合PNT体系及其关键技术［J］.测绘学报，2016，45（5）：505-510.

［2］党亚民，蒋涛，杨元喜，等.中国大地测量研究进展（2019—2023）［J］.测绘学报，2023，52（9）：1419-1436.

［3］曹风魁，庄严，闫飞，等.移动机器人长期自主环境适应研究进展和展望［J］.自动化学报，2020，46（2）：205-221.

［4］陈宇.视觉自主导航及融合导航技术研究［J］.测绘学报，2023，52（8）：1412-1420.

［5］代君，郝向阳，刘松林，等.复杂环境下无人车双重自适应定位算法［J］.中国惯性技术学报，2023，31（3）：254 -260.

［6］AGRAWAL M，KONOLIGE K.Real-time localization in outdoor environments using stereo vision and inexpensive GPS［C］.18th International Conference on Pattern Recognition （ICPR 2006），20-24 August 2006， Hong Kong， China.IEEE Computer Society，2006.

［7］AUMAYER M B，PETOVELLO G M，LACHAPELLE G.Stereo-vision aided GNSS for automotive navigation in challenging environments［C］.Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation（ION GNSS+ 2013），Nashville，TN，September2013，511-520.

［8］SCHREIBER M，KÖNIGSHOF H，HELLMUND A，et al.Vehicle localization with tightly coupled GNSS and visual odometry［C］.2016 IEEE Intelligent Vehicles Symposium （IV）.Gothenburg， Sweden， August 2016，858-863.

［9］王磊，陈锐志，付文举，等.利用视觉影像和GNSS测距信号紧耦合定位系统与方法：CN201910802812.0［P］. CN110501736A［2023-10-26］.

［10］冯祎，涂锐，韩军强，等. 一种GNSS/视觉观测紧组合导航定位算法研究［J］.全球定位系统，2021，46（6）：49 -54.

［11］YUNBIN Y.A method of vision aided gnss positioning using semantic information in complex urban environment［J］.Remote Sensing，2022，14（4）：869-869.

［12］HORN.Closed-form solution of absolute orientation using unit quaternions［J］.Journal of the Optical Society of America A，1987，4（4）：629-642.

［13］HARTLEY R.Multiple view geometry in computer vision［M］.Anhui University Press，2003.

责任编校：刘 燕，田 旭

GNSS-Assisted Visual Autonomous Localization Method in Unknown Environment

DAI Jun 1，2，3，WANG Jingyu1，MIN Jun1，Chen Xu1，ZHAO Lilong1，ZHANG Chunfeng1*

（1.School of Aerospace Engineering， Zhengzhou University of Aeronautics， Zhengzhou 450046， China；

2.Institute of Geospatial Information， Information Engineering University， Zhengzhou 450046， China；

3. Henan Key Laboratory of General Aviation Technology， ZUA， Zhengzhou 450046， China）

Abstract： Autonomous navigation and localization is the foundation of unmanned system intelligence， so continuous， stable， and reliable position service in unknown environment is especially important for autonomous navigation and localization. Aiming at the problem that GNSS cannot continuously localize in complex environments due to weak signals， poor penetration ability， and susceptibility to interference; and that visual navigation and localization is only relative， this paper proposes a GNSS-assisted visual autonomous localization method， which can provide global localization services in unknown environments. Taking the three frames of images and their corresponding GNSS coordinates as the constraint data， the GNSS coordinate system and world coordinate system transformation matrix is obtained through Horn coordinate transformation， and the relative position of the subsequent image sequences in the world coordinate system is obtained through epipolar geometry constraint， homography matrix transformation， and 2D-3D position and orientation solving， which ultimately yields the global position data of unmanned carriers in the GNSS coordinate system when GNSS is temporarily unavailable. The dataset validation show that the algorithm can be applied to the case of intermittent presence of GNSS signals， and can provide global location services with high short-time positioning accuracy. Then， we further compare the traditional state estimation and BA post-optimisation error， and the results show that compared with the traditional state estimation， the BA post-optimisation improves the localisation accuracy by 10%-20%， which proves that the algorithm has good reliability and applicability in unknown environments.

Key words：visual navigation and positioning; GNSS assisted positioning; BA optimization; horn coordinate transformation

基金项目：2024年度河南省科技攻关项目（1838）；郑州航空工业管理学院科研团队支持计划专项资助（23ZHTD01010）

作者简介：代 君，女，河南邓州人，硕士，讲师，研究方向为自主与智能导航。

*通讯作者：张春凤，女，河北秦皇岛人，硕士，讲师，研究方向为计算机及智能应用。