基于自适应超扭曲算法的燃料电池供气系统二阶滑模控制研究

摘 要：针对某小型无人机基于聚合物交换膜氢燃料电池和锂离子电池的电推进混合动力系统的实用化需求，提出了一种基于非线性自适应超扭曲算法的二阶滑模氢燃料电池供气系统控制的设计方法。通过研究燃料电池供气系统空压机空气流量与过氧比之间的关系，建立了期望空气流量与最佳期望过氧比关系的参考模型。在参考模型的基础上，引入自适应超扭曲二阶滑模控制器来优化燃料电池供气系统的性能。仿真结果表明，该控制器具有较强的鲁棒性，在负载变化和参数不确定情况下具有良好的暂态性能，同时保证了受控系统的稳定性，优化的压缩机功率配置比恒定的压缩机功率配置节能2.7%，验证了自适应超扭曲二阶滑模控制器的有效性能。

关键词：自适应超扭曲算法；燃料电池；供气系统；二阶滑模控制

中图分类号：TM911.4" "文献标识码：A" " 文章编号： 1007 - 9734 （2024） 02 - 0079- 09

0 引 言

应对气候变化的“巴黎协定”代表了全球绿色低碳转型的大方向。低碳发展，已是国家现代化建设总体发展战略定位中重点明确的目标。碳中和下，航空能源转型技术的研究成为当前航空领域面临的重要课题。新一代飞机正向更低碳、更高效、更智能、更环保的目标发展，飞机能源系统的转型正是满足这些新要求的重要支撑。

航空工业和其他交通运输行业一样，是实现碳达峰、碳中和目标的关键行业。为了解决航空工业污染排放严重、噪声大和能源转换效率低的问题，需要航空工业进行持续性和颠覆性技术创新，攻克航空工业低碳发展的关键技术，实现航空工业的低碳能源转型。

基于质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell，PEMFC）和锂电池的混合电力体系结构由于动力装置具有较高的功率和能量密度以及其推进性能的相似性，在小型载人飞机和无人机（Unmanned Aerial Vehicles，UAV）中具有巨大的应用潜力和广泛的应用前景［1］。

在混合动力系统中，燃料电池性能的控制是实现燃料电池系统最佳功率输出的重要环节。燃料电池供气系统的控制在性能优化过程中至关重要，因为在混合动力系统中，燃料电池供气系统是主要的寄生电能消耗系统，燃料电池的很大一部分能量是由空气压缩机消耗的［1］。供气系统的耗电量也是最高的，高达质子交换膜燃料电池发电量的20%。这一消耗可以通过精确控制进气压缩机来优化，从而确保燃料电池在任何工作点都有足够的氧气过剩。阴极中需要过量的氧气，以防止燃料电池在快速负载变化时损坏，这在汽车应用中很常见［2］。在负荷突然增加的情况下，PEMFC需要更多的氧气来满足需求。如果阴极中没有足够的氧气，堆电压会迅速下降，并导致膜表面出现热点或烧毁［3］。同样，当负荷迅速下降时，氧气流量也需要迅速降低。由于压缩机输出端的压力不能像流量一样快速下降，因此压缩机的运行点可能会超出喘振线（失速）而损坏。因此，需要同时解决净功率优化和过氧比控制问题。

综上所述，燃料电池供气系统的优化比其他运行参数的优化对燃料电池功率的影响更大。在大多数燃料电池控制研究中，都对PEM燃料电池系统进行了数学建模，并在供气系统中引入了不同的控制方法来优化燃料电池的性能。

在过去的几年中，众多学者围绕氢燃料电池供气系统控制领域开展了大量的研究工作，已经提出了许多控制 PEMFC 供气系统的策略，旨在最大限度地提高净功率输出并避免缺氧。

Imad Matraji等［4］提出了一种基于次优算法的鲁棒非线性二阶滑模控制器，解决了聚合物电解质膜燃料电池进气系统通过调节过氧比来保持空气压缩机在其工作范围内最佳净功率输出的问题。Pukrushpan 等［5］建立了氢燃料电池供气系统九阶模型，后来根据控制的需要在九阶模型的基础上，得到了三阶与四阶动态系统，分别采用了前馈控制和反馈控制对过氧比进行控制。Taij［6］在九阶动态模型的基础上建立了三阶模型，并且在一个 33KW 的 PEM 燃料电池上进行了仿真分析。Qihong Chen 等［7］提出了利用自回归滑动平均对非线性供气系统进行建模，并利用递归神经网络估计其系数。Cristian Kunusch 等［8］采用了二阶滑模控制算法来控制系统的过氧比，发现在输入负载变化的情况下依然能够实现比较精确地控制，鲁棒性非常强。

过氧比的模型预测控制也得到了广泛的研究，并出现了许多重要的研究成果。在文献［9］中，使用压缩机电机电压开发了一种模型预测控制器，以控制进入燃料电池的空气流量。

本文针对某小型无人机电推进混合动力系统氢燃料电池供气系统提出了一种新的非线性控制器设计方法，本文不仅是调节过氧比，而且还要确保它保持在最佳值，从而使净功率输出得到优化。为了实现这一目标，将一种基于自适应超扭曲算法的鲁棒二阶滑模控制器用于空压机控制。所用的控制律是在文献［10］工作的基础上提出的，其目的是为了抵消抖振现象，并在载荷变化和参数不确定性下保持经典滑模的鲁棒性和有限时间收敛特性。

用于控制设计的供气系统非线性动态模型是四状态模型。该模型的优点是它适用于燃料电池的整个工作范围，并且保证压力动态不被忽略。此外，对参数不确定性进行了形式化描述，并将其包含在模型中。该方法在控制器设计中直接考虑了不确定性，所得到的非线性控制器是鲁棒的，并被证明在任何平衡点附近和参数不确定性下都能保证性能。

本文对所提出的控制器进行了软件仿真分析实验验证。实验结果表明，闭环系统稳定，具有良好的暂态特性。本文提出的新的控制器设计能够满足无人机电推进混合动力系统控制需要对模型不确定性、传感器偏差、传感器噪声和时间延迟具有鲁棒性，同时还要足够快速和准确，以适应小型飞机相对灵活的动态特性。

除去引言，文章内容分为以下几个部分：第一节中建立了质子交换膜氢燃料电池供气系统的动力学模型；第二节中详细介绍了二阶滑模的基本概念；第三节中介绍了控制设计；第四节中给出了仿真实验结果；第五节中给出了结论。

1 问题表述

在设计控制之前需要对系统属性进行初步定义。本节讨论供气系统模型和控制目标。

1.1" PEMFC供气系统模型

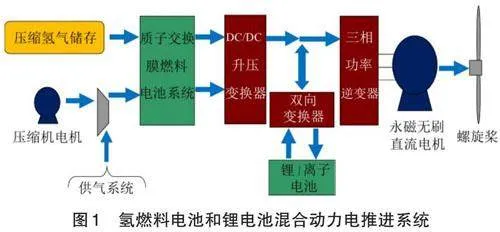
质子交换膜氢燃料电池和锂电池供电的混合电动结构主要由质子交换膜氢燃料电池系统、锂电池、DC/DC升压变换器、双向变换器和带有三相逆变器的永磁直流无刷电机组成。采用质子交换膜氢燃料电池系统作为一次电源，锂离子电池作为二次电源。DC/DC单向变换器提升聚合物交换膜氢燃料电池输出电压并调节直流母线电压。双向变换器在调节直流母线电压的同时改变电池的功率流向以充电或放电。永磁无刷直流电机在所有飞行条件下都能推动飞机前进。三相功率逆变器将直流母线电流转换为交流电流信号，并连接到永磁无刷直流电机。电机控制器根据霍尔传感器反馈产生逆变器PWM信号。氢燃料电池和锂电池混合动力电推进系统的示意图如图1所示［1］。

建立 PEMFC 供气系统的4阶状态方程如下式所示。其中4个状态变量[x1]、[x2]、[x3]、[x4]分别为阴极氧气压力[PO2]、阴极氮气压力[PN2]、空气压缩机转速[wcp]以及供气管压力[Psm]。电堆的负载电流[Ist]作为系统输入的扰动量由[ξ]表示。[u]是系统输入，在这里表示的是空气压缩机电机二次电流[Iq]。

[ x1=RTstKca，inKO2MO2Vca1+Watmx4-x1-x2-Psat-RTstKca，outVcaMO2x1x1+x2+Psat⋅x1+x2+Psat-Patm-RTstKca，out4VcaF⋅ξ" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " （1）]

式（1）中，[R]为普适气体常数，[R=8.314J/（mol.K）]；[F]为法拉第常数，[F=9.64853×104C/mol]；[Tst]为电堆温度， [Tst=353K]； [Kca，in]为阴极入口孔板常数； [KO2]为氧气在阴极输入流量中的占比系数；[MO2]为氧气的气体摩尔质量；[Vca]为阴极体积；[Watm]为大气流量；[Psat]为饱和压力；[Kca，out]为阴极出口孔板常数；[Patm]为大气压力。

[x2=RTstKca，inKO2MO2Vca1+Watmx4-x1-x2-Psat-" " " RTstKca，outVcaMO2x2x1+x2+Psat⋅x1+x2+Psat-Patm] （2）

[x3=-ηcmKtKvJcpRcmx3-CpTatmηcp⋅x4Patmγ-1γ-1Jcpx3Wcp+" " " " " " " " ηcmKtJcpRcmu] （3）

式（2）和（3）中，[ηcm]是供气系统空气压缩机电机的机械效率；[Kt]、[Kv]、[Rcm]是电机常数；[Jcp]是空气压缩机转动惯量；[Cp]是空气定压比热容（取[Cp=1004J/kg.k]）；[Tatm]为大气温度；[ηcp]为空气压缩机效率；[γ]是空气热比例系数；[Wcp]是空气压缩机流量。

[x4=RVsmTatm+Tatmηcpx4Patmγ-1γ-1⋅" " " " " " " Wcp-Kca，in（x4-x1-x2-Psat）] （4）

式（4）中，[Vsm]是供气管体积。

过氧比（[λO2]）指的是阴极供应[O2] 流量[WO2，in]与其反应消耗[O2] 流量[WO2，rct]的比值，具体表达式由式（5）所示：

[λO2=WO2，inWO2，rct] （5）

当过氧比[λO2lt;1]时，表明反应中氧气的消耗量大于氧气的供应量，氧气供应量不足，这会影响电化学反应的进行，甚至会造成氧气匮乏现象的发生，从而导致电池电堆和整个系统输出动态性能的下降，甚至会对电堆的安全稳定运行带来影响。故在电池稳态运行中，要保证过氧比[λO2gt;1]。

在PEMFC运行中，过氧比[λO2]不能过大，因为[λO2]过大表示氧气供应量较大，空气压缩机就需要消耗更多的功率来供应氧气，如果电堆输出功率的增加是有限的，就会造成系统有效输出功率的降低。故在运行中，过氧比[λO2]应该保持在合适的值上（一般控制在[λO2=2]）。

燃料电池的功率由电堆电压与电流的乘积可得，空气压缩机所消耗的功率由空气压缩机电压与电流的乘积可得，净功率[Pnet]为燃料电池功率减去空气压缩机消耗功率。由此可得[Pnet]：

[Pnet=VstackIst-VcmIcm] （6）

式（6）中，[Vstack]为 PEMFC 电堆电压；[Vcm]是空气压缩机电压；[Icm]是空气压缩机电流。其中，

[Icm=1Rcm（Vcm-kvwcp）] （7）

通过上述对控制系统以及控制目标的研究，得到燃料电池的整个供气系统非线性系统模型可表示为：

[x=f（x， u， ξ）x=PO2，PN2， wcp，Psmy=λO2， Pnetu=Iqξ=Ist] （8）

1.2" 控制目标

控制目标是使燃料电池供气系统在给定空气压缩机的电机二次电流[Iq]下，过氧比[λO2]的值在最优值运行。

通过对燃料电池供气系统进行分析可知空气流量与过氧比之间存在代数关系，通过调节 PEMFC 供气系统的实际输出流量[Wcp] 与期望流量[Wcp，ref]的偏差，进而改变空压机的电机电流以满足过氧比数值最优。

在实际应用中，取得最大净功率时的过氧比值是随着负载电流变化而变化的，为了能取得更好的控制性能，需要在不同的负载电流处得到取得最大净功率的过氧比值。根据得到的数据进行线性拟合得出了最优过氧比[λO2opt]与负载电流[Ist]间的关系，即：

[λO2opt=-0.0017Ist+2.5973] （9）

通过公式推导出期望流量[Wcp，ref]与[λO2，ref]的关系：

[Wdryair，ref=1χO2WO2，inref] （10）

由式（5）可知，[λO2=WO2，inWO2，rct⇒λO2，ref=WO2，inrefWO2，rctref] （11）

[WO2，inref=λO2，refWO2，rctref] （12）

[WO2，rctref]为氧气的消耗参考量，由电化学反应方程式得：

[WO2，rctref=MO2nIst4F] （13）

由上述公式推导可以得到参考过氧比下干燥空气流量得：

[Wdryair，ref=1χO2λO2，refMO2nIst4F] （14）

考虑到空气相对湿度对空压机流量的影响，最终得到空压机流量的参考值为：

[Wcp，ref=（1+Ωatm）1χO2λO2，refMO2nIst4F] （15）

式（15）中，[χO2]是空气中氧的摩尔分数；[Ωatm]是空气相对湿度；[λO2，ref]为过氧比的参考值。将式（9）代入式（15），可以得到 [Wcp，ref]与负载电流[Ist]的关系为：

[Wcp，ref=（2.5973-0.0017Ist）（1+Ωatm）1χO2MO2nIst4F] （16）

2 控制方法

在高性能线性/非线性控制器的发展过程中，滑模控制是控制具有匹配扰动/不确定性的扰动系统的选择之一。一般我们可以使用高阶滑模控制技术或者自适应滑模控制器来解决控制中出现的颤振。高阶滑模控制技术允许在存在干扰/不确定性的情况下将滑动变量及其连续导数驱动为零，从而提高滑动变量稳定的准确性。然而，高阶滑模控制器的主要挑战是使用滑动变量的高阶时间导数。基于著名的超扭曲二阶滑模算法和增益交换控制器只需要测量滑动变量，而其他二阶滑模控制器还需要滑动变量的时间导数。

本文将增益适应和高阶滑模控制结合在一起所获得的自适应超扭曲算法控制器［10］用来控制氢燃料电池供气系统的过氧比，使得用于无人机电推进混合动力系统的输出净功率达到飞行器整个飞行包线内的最优状态。

考虑一类单输入不确定非线性系统

[x=f（x）+g（x）u] （17）

其中，[x∈X⊂Rn]是状态向量（[X]是紧凑集）；[u∈R]是控制函数；[f（x）∈Rn]是可微的且部分已知的向量场。

假设

（A1） 设计一个滑动变量[σ=σ（x， t）∈R]，以便在滑动模式[σ=σ（x， t）=0]下实现系统（17）理想的动态补偿。

（A2） 系统（17）与滑动变量[σ（x， t）]相对于[u]的相对度数等于1，内部动态是稳定的。

因此，可以呈现输入—输出动态

[σ=∂σ∂t+∂σ∂xf（x）︸a（x，t）+∂σ∂xg（x）︸b（x，t）u=a（x， t）+b（x， t）u] （18）

此外，假设

（A3） 函数[b（x， t）∈R]是不确定的，可以表示为

[b（x， t）=b0（x， t）+Δb（x， t）] （19）

其中，[b0（x，t）gt;0]是已知函数，[Δb（x， t）]是有界扰动使得[Δb（x， t）b0（x， t）=γ（x， t）≤γ1lt;1]，[∀x∈Rn]和[t∈0，∞]具有未知边界[γ1]。

（A4） 函数[a（x， t）∈R]表示为

[a（x， t）=a1（x， t）+a2（x， t）] （20）

有界项" " " " "[a1（x， t）≤δ1σ12a2（x， t）≤δ2] （21）

其中，有限边界[δ1， δ2gt;0]存在但未知。

最后，得到

[σ=a（x， t）+1+Δb（x， t）b0（x， t）︸b1（x，t）ω] （22）

其中，[ω=b0（x， t）u]，从（A3）可以得到

（A5）" " " "[1-γ1≤b1（x， t）≤1+γ1]" " " "（23）

问题是驱动滑动变量[σ]及其导数[σ]在存在未知边界[δ1、δ2、γ1gt;0] 的有界加性（21）和乘性（19）扰动的情况下，通过连续控制而不高估控制增益并在有限时间内归零。

本文寻求一种自适应增益超扭曲算法（adaptive super-twisting control law，ASTW），该算法能够通过生成连续控制函数（颤振衰减）来解决这个问题，从而使其增益适应未知边界的未知加性和乘性扰动，并且没有控制增益高估。

考虑以下超扭曲算法（super-twisting control law，STW）控制

[ω=-ασ12sign（σ）+vv=-β2sign（σ）] （24）

其中，自适应增益

[α=α（σ， σ， t）β=β（σ， σ， t）] （25）

系统（22）的解可以从 Filippov 的意义上理解。 假设不确定函数[b1（x，t）]是一个不确定的分段常数，控制系统（22）和（24）可以重写为

[σ=-αb1（x， t）σ12sign（σ）+ω∗+a1（x， t）ω∗=-βb1（x， t）2sign（σ）+a2（x， t）+b1（x， t）vω∗（0）=0]"（26）

其中，[ω∗=a2+b1（x，t）v]。为简洁起见，用[b1]和[a2]分别表示术语[b1（x，t）]和[a2（x，t）]。假设术语[b1v]的边界是未知边界[δ3gt;0]，即

[b1v≤b120tβ dτ≤δ3] （27）

证明了自适应增益[β=β（σ，σ，t）]有界于不确定边界[β∗gt;0]，即[β≤β∗]。那么等式（27）成为

[b1v≤12b1β∗t≤δ3] （28）

值得注意的是，式（28）在任何有限的时间间隔上都有效，因此，系统（26）的动态仅在有限的时间间隔上考虑。最后，不确定函数[χ（x，t）=a2（x，t）+b1v]的边界存在但未知。即

[χ（x， t）≤δ2+δ3=δ4] （29）

控制设计问题归结为设计ASTW控制（24）—（25），当存在未知边界[δ1、δ2、γ1gt;0]的有界加法（21）、（29）和乘法（19）扰动时，在有限时间内驱动（26）给出的[σ、σ→0]。

设计ASTW的思想是动态增加控制增益[α（t）]和[β（t）]，直到2阶滑模建立。然后，增益将开始减少。当滑动变量或其导数开始偏离2阶滑动模式下的平衡点[σ=σ=0]时，应立即逆转这种增益降低。因此，应构造一个检测滑动模式破坏开始的规则（检测器），并将其纳入允许不高估控制增益[α（t）]和[β（t）]的ASTW控制律中。通过引入一个域[σ≤μ]来设计该“检测器”，该域的用法如下：一旦达到该域，增益[α（t）]和[β（t）]开始动态减小，直到系统轨迹离开该域；随后，增益开始动态增加，以便在有限时间内迫使轨迹返回到域。

考虑系统（26），假设函数[a1（x， t）]、[a2（x， t）]和[b1（x， t）]对于某些未知增益[δ1、δ2、γ1gt;0]满足假设A3和A5 。那么，对于任何初始条件[x（0）]和[σ（0）]，存在一个有限时间[tFgt;0]和一个参数[μ] （只要满足条件， [δ4]被定义为[δ4=δ2+δ3]，

[αgt;δ1（λ+4ε2）-ε（4δ4+1）λ（1-γ1）+2εδ1-2δ4-λ-4ε2212ελ（1-γ1）]成立，如果[σ（0）gt;μ]），从而通过具有自适应增益（[α（0）gt;αm]）的ASTW控制（24）建立一个实2阶-滑动模式，即[σ≤η1]和[σ≤η2]，[∀t≥tF]

[α=ω1γ12sign（σ-μ），" nbsp;if" αgt;αm" " " " η，" nbsp; " " " " " " " " " " " " " " if" α≤αmβ=2εα] （30）

其中，[ε]、[λ]、[γ1]、[ω1]、[η]是任意正常数，[η1≥μ]，[η2gt;0]，参数[αm]是任意小的正常数。

控制律的收敛如图2所示。关于算法稳定性证明的详细证据可以在文献［10］中找到。

3 控制设计

PEMFC 供气系统滑模控制的原理框图如图3所示。

为了实现过氧比的控制首先要选择合适的切换函数[S（x）]。通过对供气系统进行分析空气流量与过氧比之间存在代数关系，选取 PEMFC 供气系统的实际输出流量[Wcp] 与期望流量[Wcp，ref]的偏差作为滑模控制的切换函数[S（x）] 。空气压缩机的电机电流作为滑模控制的输入。

滑模控制的切换函数[S（x）]为：

[S（x）=Wcp-Wcp，ref] （31）

控制函数 [u（x）]的选择由式（18）可知。其中，函数[a（x， t）]和[b（x， t）]在[x∈X]上有界，函数[b（x， t）]满足关于[x∈X]的假设A3，此外，函数[a（x， t）]可以写为[a=a0+Δa]。

可得出控制函数[u（x）]为

[u（x）=1b0（-a0+ω）] （32）

其中，控制输入[ω]由式（24）定义，增益[α]和[β]由式（30）定义。

4 仿真结果

仿真中使用的参数如表1所示。

为了评估控制器的性能，仿真器被置于100到400安之间的负载电流下，如图4所示。

电池的电压在 55 到 70 V 之间变化，如图5所示。过氧比控制的目标是将过氧比保持在式（9）所给出的最佳值。

图6显示的是空气压缩机的流量变化，可以看出在负载电流变化时空气压缩机流量也会产生波动，随后就与参考空气压缩机流量稳定保持一致。

系统指令电机的二次电流在0到5 A之间变化，如图7所示。

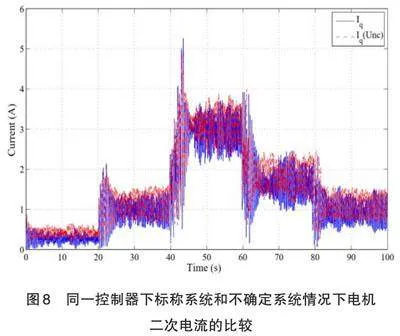
图8通过将扰动系统与标称无扰动情况进行比较显示了扰动系统控制的演变。受扰系统的控制由Iq（Inc） 指定的曲线表示，命令会演变，以补偿参数变化。在图8中，虚线表示存在不确定性时的行为，而实线表示标称系统的行为。从仿真结果中可以得出结论，尽管有参数变化和负载变化，但所提出的控制器仍保持良好的性能，控制器增益没有任何变化。

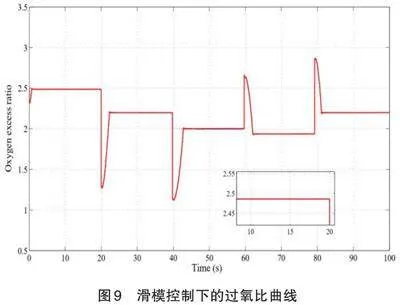
二次电流的比较仿真分析实验中，基于自适应超扭曲（AST）算法混合动力系统性能，过氧比和净功率变化情况如图9和图10所示。

图9显示的是供气系统过氧比在滑模控制下的变化曲线。在第20S 时负载电流突然从100A增加到200A，使得供气系统氧气流量被氢燃料电池电堆迅速消耗，过氧比由原来的2.5迅速变为1.26，随后空气压缩机的电压上升使得空气输入流量增加导致过氧比迅速上升；在第23s左右时过氧比值稳定在新的过氧比参考值附近；在第60s时负载电流从400A下降到300A，这时由于空气压缩机还是按照原来氧气的消耗为燃料电池供气，所以过氧比瞬时上升，空气压缩机电压下降，控制过氧比也跟着下降，最终稳定到新的过氧比参考值附近［1］。在负载电流变化时，过氧比值一直在1.2至2.8之间，没有发生缺氧现象，滑模控制稳定后稳态误差基本为0。

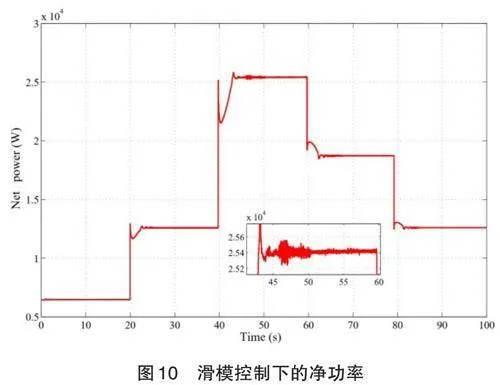
图10为滑模控制下净功率的图像，当负载电流阶跃变化时，滑模控制下的净功率发生的变化较小，没有出现净功率小于 0 的情况。

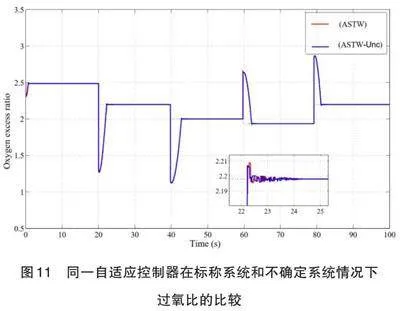
为了验证控制器对这些不确定性的适应性，应用了不确定参数的相同变化。图11表示控制器在标称系统和不确定系统的过氧比。具有不确定性的过氧比用（Unc）表示。

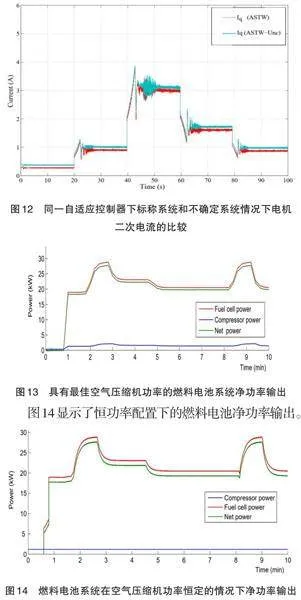
过氧比的比较控制律如图12所示。在不确定性期间应用的命令用 （Unc） 表示。不确定系统的控制律会演变以补偿参数变化。因此，可以从这些结果中得出结论，尽管存在干扰和参数变化，所提出的自适应控制仍能保持良好的性能，而控制器增益没有任何变化。

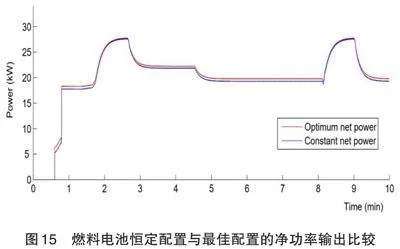
在最佳空气压缩机功率模式和恒定空气压缩机功率模式下，比较了 PEM 燃料电池系统的性能。从仿真实验对比分析结果可以看出，氢燃料电池堆产生最大净功率输出的最佳空气压缩机功率配置是负载跟踪过程，与恒定空气压缩机功率模式相比，该过程显示出显著的最佳能量管理效果。在恒定空气压缩机功率配置中，空气压缩机功率始终保持在2KW状态，这是整个无人机飞行任务期间的最高空气压缩机功率要求。图13显示了在最佳空气压缩机功率运行期间燃料电池系统的净功率输出。空气压缩机的工作功率随着燃料电池电流的变化而呈现动态变化的结果［1］。

二次电流的比较图14显示了恒功率配置下的燃料电池净功率输出。

在图15中，PEM 燃料电池的净功率输出在空气压缩机恒定功率和最佳功率配置之间进行了比较。结果表明，在最佳空气压缩机功率配置的充电状态下，燃料电池能量可节省约 2.7%。

5 结 论

供气系统空气压缩机是质子交换膜燃料电池中耗能最大的设备。因此，对供气系统进行控制是非常重要的。本文提出了一种调节过氧比的非线性自适应超扭曲二阶滑模控制器来优化PEMFC的功率。该控制器通过提供一个压缩机空气流量参考来控制过氧比。PEMFC模型基于代表阴极侧进气系统的4个状态方程，参数不确定性已被形式化并集成到动态模型中。将自适应超扭曲控制算法应用于二阶滑模控制结构，从形式上证明了该控制器对所考虑的参数不确定性的鲁棒性和不敏感性。仿真结果表明，基于自适应超扭曲算法的二阶滑模控制器提供了一种新的有效方法，可优化燃料电池供气系统空气压缩机的性能，从而可以从混合动力系统获得最大的净功率输出，优化了混合动力电推进供气系统的能量利用。

参考文献：

［1］李勇，韩非非，张昕喆.基于自适应神经模糊推理算法的无人机电推进燃料电池供气系统性能优化［J］.推进技术，2021，42（6）：1395-1409.

［2］SALAH L，IMAD M，FAYEZ S A，et al.Load governor based on constrained extremum seeking for PEM fuel cell oxygen starvation and compressor surge protection［J］. International Journal of Hydrogen Energy，2013（38）：14314-14322.

［3］PUKRUSHPAN J，STEFANOPOULOU A，PENG H. Control of fuel cell power systems： principles， modeling and analysis and feedback design［M］.Springer：2004.

［4］IMAD M， SALAH L，SAMIR J，et al.Robust control of the PEM fuel cell air-feed system via sub-optimal second order sliding mode［J］.Applied Energy，2013（104）：945-957.

［5］PUKRUSHPAN J T，STEFANOPOULOU A G ，PENG H .Control of fuel cell breathing［J］.Control Systems IEEE， 2004，24（2）：30-46.

［6］TALJ R J，HISSEL D，ORTEGA R，et al.Experimental Validation of a PEM Fuel-Cell Reduced-Order Model and a Moto Compressor Higher Order Sliding-Mode Control［J］. IEEE Transactions on Industrial Electronics，2010，57（6）：1906-1913.

［7］CHEN Q，GAO L，DOUGAL R A，et al.Multiple model predictive control for a hybrid proton exchange membrane fuel cell system［J］.Journal of Power Sources，2009，191（2）：473-482.

［8］KUNUSCH C，PULESTON P F，MAYOSKY M A，et al. Sliding Mode Strategy for PEM Fuel Cells Stacks Breathing Control Using a Super-Twisting Algorithm［J］.IEEE Transactions on Control Systems Technology，2009，17（1）：167-174.

［9］GRUBER J K，DOLL M，BORDONS C.Design and experimental validation of a constrained MPC for the air feed of a fuel cell［J］.Control Eng Pract，2009，17（8）：874-885.

［10］SHTESSEL Y，TALEB M，PLESTAN F.A novel adaptive-gain super twisting sliding mode controller： methodology and application［J］.Automatica，2012，48（5）：759-769.

责任编校：刘 燕，田 旭

Research on Second-order Sliding Mode Control of Fuel Cell Gas Supply System Based on Adaptive Super-twist Algorithm

LI Yong，GUO Qing，ZHANG Kaixuan，ZHANG Xiang，DANG Li

（ School of Aeroengine，Zhengzhou University of Aeronautics ， Zhengzhou 450046，China）

Abstract： Aiming at the practical application of the electric propulsion hybrid power system of a small UAV based on polymer exchange membrane hydrogen fuel cell and lithium-ion battery， a design method of second-order sliding mode hydrogen fuel cell gas supply system based on nonlinear adaptive super-twist algorithm is proposed. Based on the study of the relationship between the air flow rate and the oxygen excess ratio of air compressor in fuel cell gas supply system， a reference model for the relationship between expected air flow rate and optimal expected oxygen excess ratio is established. Based on the reference model， an adaptive super-twisted second-order sliding mode controller is introduced to optimize the performance of the fuel cell gas supply system. The simulation results show that the controller has strong robustness， good transient performance in the case of load changes and parameter uncertainties， and ensures the stability of the controlled system. The optimized compressor power configuration saves 2.7% more energy than the constant compressor power configuration， which verifies the effective performance of the adaptive super-twist second-order sliding mode controller.

Key words：adaptive super-twist algorithm；fuel cell；gas supply system；second-order sliding mode control

基金项目：2023年国家大学生创新创业训练计划项目（202310485001）；河南省重点研发与推广专项（科技攻关）（232102240071）；郑州航空工业管理学院大学生创新创业训练计划项目（“夸父追日”-临近空间太阳能混合动力飞行浮空器关键技术研究）

作者简介：李 勇，男，河南确山人，副教授，硕士生导师，研究方向为飞行器控制及航空动力装置控制技术。