复合材料补片参数对粘结修补含裂纹金属板结构振动特性的影响分析

摘 要：本文研究了粘结复合材料修复对裂纹金属板振动特性的影响规律。研究了补片几何参数对振动水平和修复效果的影响。振动水平由第一模态频率、模态阻尼损耗因子和裂纹尖端平面外的振幅表征。通过应力强度因子的幅值来评估修复效果。研究结果显示，修复后的应力强度因子会随着模态阻尼损失因子的增加而呈现渐进行为，尤其是在将阻尼材料插入复合材料补片的情况下，这种趋势更加显著。

关键词：补片；维修参数；振动控制；裂纹金属板

中图分类号：V229+.7" " " " " " " " "文献标识码：A" " " " "文章编号：1007 - 9734 （2024） 02 - 0038 - 08

0 引 言

在航空航天领域，金属结构在共振条件下容易出现裂纹，这给飞机的安全飞行带来很大的隐患[1]。由于经济因素，许多情况下很难及时更换存在裂纹的金属结构。因此，提高存在裂纹的金属结构的承载能力是一项极具挑战性的任务。近年来多种修复方法被应用于含裂纹金属板的修复，其中复合补片修复法最为常见且有效。由于该方法具有高强度与刚度比、耐候性以及高疲劳寿命，因此被成功应用于修复受损的飞机和海洋船体结构[2-5]。许多研究人员深入研究了补片参数对结构修复性能的影响[6-9]，这些参数包括贴片形状、贴片材料、贴片尺寸、贴片对称性以及粘合剂厚度等。然而，已有的研究大多集中在薄壁板的面内加载上，而忽略了复合材料修复的弯曲性能。薄壁加强筋在军用飞机和火箭结构中应用极其广泛。为了提高飞机的使用寿命，我们需要对加强筋以及复合材料补片修理所引起的弯曲效应进行严格的分析。

Northrop在复合材料修复中提出了弯曲修正因子的概念，用于计算含裂纹板材表面的表观应力强度因子，该方法被广泛用于有弯曲效应的情况。Ting［10］等人研究了含加强筋结构的复合材料修复问题，并指出应力强度因子是加强筋结构的弱函数。Jones［11］等人提出并应用了加强筋修正系数的概念，将现有的用于裂纹金属蒙皮复合材料修理的设计公式扩展到含加强筋机翼蒙皮的粘接修理上。研究认为，加强筋和修补所用的附加补片的弯曲效应均可体现在弯曲修正系数上，并进一步推导出应力强度因子与这些影响因素的关系［12］。研究表明表观应力强度因子可以近似为加强筋截面惯性矩的函数。此外，Jones［13］等人提出了一种权函数技术，用于计算复合材料修复裂纹的应力强度因子，这些裂纹来自加强筋在任意载荷下的内部缺口、腐蚀混合或自由边缘。

然而，以上工作基本是针对飞机的面内载荷进行的，而飞行环境可导致飞机薄壁结构产生较为明显的面外振动。如果飞机被修复结构受到显著的面内静载荷影响或是由于面外动载荷引起显著振动，则修复后的补片下也会形成并产生新的裂纹，修复不能维持很长时间。最终，可能需要更换掉整个被修复结构。Fredell［14］在实验中提出，使用Glare补片修复的结构比使用硼—环氧数值补片修复的结构的疲劳性能更好。Jones［15］给出的解释是，使用Glare补片修复的结构具有显著的剪切模量。因此，提高修复后结构的疲劳寿命和结构强度是一个重要问题，传统的复合材料补片技术亟待改进。Rogers［16］设计了耐久性补片，该补片是在含裂纹区域粘贴一个弹性椭圆形层压板，中间夹了阻尼层。Ikegami［17］等人采用耐久性补片技术对B-52、F-15和C130进行了修复。他们发现，使用耐久性补片不仅可以提高受损区域的强度，补片中增加的阻尼处理还可以抑制振动响应，提高飞机的寿命。然而，他们没有对贴片参数进行详细研究。实际上，耐久性补片是一种由两个弹性层和一个粘弹性阻尼材料层组成的夹层结构。

九宫格式加筋板是飞机上广泛使用的典型加筋板构型。Ｌiu［18］等人探讨了九宫格式加筋板优化约束阻尼处理的振动抑制问题。Ｌiu［19］等人还研究了裂纹参数和加强筋布局对中心贯穿裂纹的九宫格式加筋板应力强度因子的影响。然而，他们在研究中没有考虑耐久性补片对含裂纹结构的修复效果。大多数复合材料补片修复的理论模型采用了简化的二维模型，并只考虑了弯曲因子的面内加载。然而，在振动条件下，面外载荷对结构的影响不容忽视，二维模型很难表征这种复杂的振动应力状态，一般考虑采用三维模型来模拟预测结构在振动条件下的应力状态。在共振条件这种极端的振动条件下，阻尼处理是抑制结构振动响应水平的最重要措施。在补片修复结构中，裂纹的产生和扩展主要受裂纹尖端的振幅和应力强度因子的影响。

因此，本文建立了含中心贯穿裂纹的2024-T3铝合金九宫格式加筋板结构的三维有限元模型。针对共振环境下裂纹结构，采用不同尺寸和构型的复合材料补片对其进行修复，并对不同补片的九宫格式加筋板的振动性能进行了定量分析。着重讨论单面和双面补片修复的效果，并进一步研究了补片面积、补片厚度、复合材料纤维取向及耐久性补片中阻尼层厚度对修补结构第一模态频率、裂纹尖端稳定应力强度因子Kmax的幅值和结构的振动水平的影响。

1 振动基本理论

在共振情况下，提高结构的阻尼性能是抑制结构在固定边界条件下动力响应的重要方法［20］。对于具有粘性阻尼的单自由度（SDOF）系统，在简谐力（[ft=F0sint]）作用下，运动方程可表示为：

[-kx-cx+F0sinωt=mx]" " " " " " " " " " " " " " " " （1）

式中，m为当量质量，c为粘性阻尼系数，k为刚度。F0为激振力的振幅，ω为激振频率。此外，x表示响应位移。重新排列上面的方程可以得出：

[mx+kx+cx=F0sinωt]" " " " " " " " " " " " " " " " " "（2）

或

[x+2ζωnx+ω2nx=F0msinωt]" " " " " " " " " " " " " " （3）

式中，ωn为角频率，单位为rad/S，ζ为阻尼比。相应的稳态位移为：

[χ=F0k1-ωωn2+2ξωωn2]" " " " " " " " " " " " " " " （4）

当ω/ωn=1且阻尼比等于零时，位移振幅[χ→∞]。

随着阻尼比ζ的增大，共振时的最大稳态幅值减小，并向ω/ωn lt;1方向移动。当阻尼比很小时可以忽略不计，位移幅值逐渐趋于稳态。如果基础结构的阻尼比变大，则稳态时的位移幅值一定很小。一般情况下，复合材料贴片的阻尼高于金属结构的阻尼［21］。因此，在复合材料补片修补金属板时，必须考虑复合材料补片的阻尼性能。

一般情况下，复合补片修复金属板可以假定为线弹性问题。基于单自由度的线性叠加法可以计算振动幅值。因此，振动振幅随时间的变化曲线与SDOF中的趋势相似，记录最大振幅Umax以表征共振时的振动水平。

在线弹性断裂域中，裂纹尖端周围的应力场和位移场由SIF（K）表示。定义SIF或K。在裂纹尖端的应力强度因子KI、KII和KIII由位移场的跳跃表示。考虑到裂纹尖端M点的局部笛卡尔坐标系具有裂纹切平面的法向量（Y方向）和裂纹尖端的切向量（X方向），因此三个应力强度因子在（X，Y，Z）坐标系中通过以下渐近关系给出［22］：

[KI（s，t）=limR→0（E8（1-υ2）{uY（R，s，t）}2πR）KII（s，t）=limR→0（E8（1-υ2）{uX（R，s，t）}2πR） KIII（s，t）=limR→0（E8（1+υ）{uZ（R，s，t）}2πR）]（5）

式中，R表示在（X，Y）平面中到裂纹尖端点M的距离，E为弹性模量，ν为泊松比，s为沿裂纹前沿的曲线横坐标，t为时间，[{uN（R， s， t）}]，[{uT（R，s，t）}]以及[{uV（R， s， t）}]表示沿着裂纹前沿的局部法线（Z方向）跨越裂纹到裂纹前沿的跳跃算子，指向实体内部。疲劳裂纹扩展速率与K的范围有关，通常表示为△K。在目前的工作中，考虑了在谐振时稳态条件下的KI（s，t）的最大值（KI，max）。

2 共振条件下九宫板结构的有限元建模

2.1" 几何形状和材料

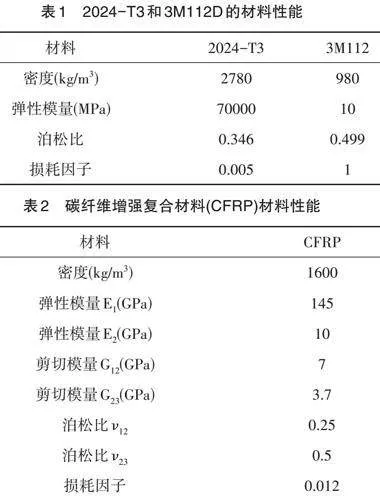
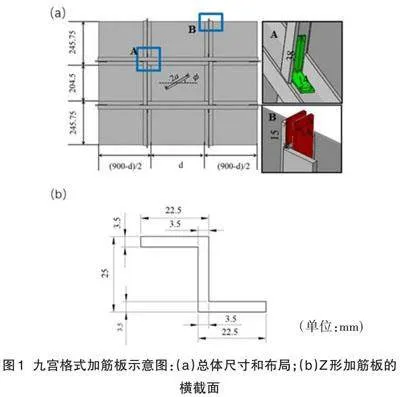
九宫格式加筋板示意图如图1所示。面板的尺寸为900×700×1.6mm3。加强筋之间的距离如图1（a）所示，加强筋以不对称的方式放置在面板上。加强筋的横截面为“Z形”，厚度为3.5mm，详细尺寸如图1（b）所示。两个矩形角板系在Z形加强筋的末端。两个角板的厚度为2mm。在本文中，假设中心裂纹长度2a和倾角θ分别为30mm和0度。

九宫格式加筋板的所有部件（面板、角撑架和加强筋）均采用Al-2024 T3材料，并采用碳纤维增强复合材料（在下文中简化为CFRP）修复裂缝区域，并在CFRP中插入阻尼材料3M112D以研究其对面板的阻尼效果。表1和表2中列出了模拟中使用的所有材料的材料特性。

对于修补过程中，补片的尺寸取裂纹长度尺寸的4至5倍［23］。在本文文中，椭圆贴片的长轴长度为300mm，短轴长度为200mm。贴片的厚度使用以下关系式进行估计：

[1.5Et≥Eptp≥Et]" " " " " " " " " " " " " " " " " " " " " " " （6）

其中Ep是补片的弹性模量，tp是补片的厚度；E是金属板的弹性模量，t是金属板的厚度。

由表2可知，九宫格式加筋板面板金属的弹性模量E为70 GPa，厚度t为1.6mm。当补片铺层垂直于裂纹方向时，Ep=145GPa，则0.77mmlt;=tplt;=1.16mm。碳复合材料补片的最佳厚度大于或等于0.77mm且小于或等于1.16mm。在模拟中分析了各种补片厚度，以研究受试面板的振动水平的变化和响应。此外，还研究了不同角度铺设顺序的单向CFRP层压板补片。

2.2" 有限元模型

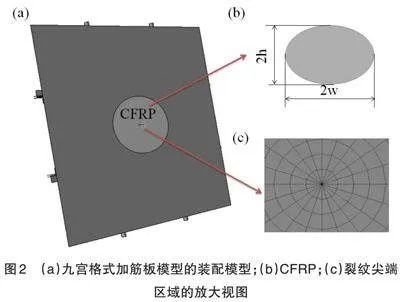
九宫格式加筋板在整体结构中采用网格尺寸为5mm的三维四边形线性壳单元进行了网格划分。需要注意的是，裂纹尖端的网格尺寸在有限元建模中非常重要。当裂纹尖端的网格尺寸小于裂纹长度的0.02倍时，可以忽略裂纹尖端的奇异性［24］。因此，使用尺寸为0.2mm的三维三角形线性单元对裂纹尖端区域进行网格划分。九宫格式加筋板的节点数和单元数分别为36745和35231。复合材料补片的总体网格尺寸为2mm。九宫格式加筋板和CFRP的装配模型如图2（a）所示。CFRP为椭圆形，长轴为2w，短轴为2h，如图2（b）所示。裂纹尖端区域的放大视图如图2（c）所示。在网格尺寸分别为2mm、5mm和10mm的情况下进行了网格灵敏度分析，结构的第一模态频率之间的差异小于1%。

在有限元建模中，要保证复合材料补片和粘贴面板没有相对运动，应采用绑定的连接方式。建立三维有限元模型之后，采用Frequency分析步求解结构模态频率和模态振型，随后在九宫板表面施加垂直于面板的面压载荷P=P0 sin（ω1t），幅值P0为100 MPa，ω1为含中心裂纹九宫板结构的第一阶模态圆频率；t为共振作用时间，文中取值为1s，在有限元软件中采用模态动力学方法来实现这一工况，研究单双面修补，改变复合材料补片面积、补片厚度、补片铺层角度以及阻尼性能对共振九宫板结构的一阶模态阻尼、裂尖处的幅值和I型动态应力强度因子最大值KI，max的影响。

应用有限元软件ABAQUS/CAE进行了所有模拟。利用接缝来确定裂纹，并通过频率分析步长获得修复后加筋板的模态频率。采用位移外推法计算稳定应力强度因子振幅KI，max。通过模态动力学分析步骤获得裂纹前缘的位移和结构的振幅。使用裂纹尖端的KI，max和法向振幅U3，max来表征结构的响应。

3 复合材料修补含中心穿透裂纹九宫板结构的结果分析与讨论

3.1" 单双面修补的影响

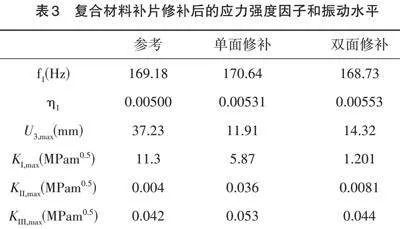
对于含裂纹平板结构，双面修补往往能够显著地降低其应力强度因子幅值，因而在复合材料胶结修补中得到广泛的应用。而对于四边固支的含中心裂纹九宫板结构，因结构在振动方向的不对称性，采用单、双面复合材料修补对结构抑振修补效果的影响有待进一步研究。本节采用的椭圆形复合材料补片厚度为0.8mm，长轴为300mm，短轴为200mm，九宫格式加筋板的裂纹长度为2a=30mm且倾角为φ=0（如图2所示）。单面修补时将补片粘贴在筋条异侧裂纹正上方，双面修补则是在裂纹两侧对称粘贴。表3列出了通过单面和双面修复的裂纹尖端的最大稳态应力强度因子振幅（包括KI，max，KII，max和KIII，max）和振动水平（包括面板外的最大振动振幅U3，max，第一模态频率f1和模态阻尼η1）的数值预测结果。其中参考件为未修补的含裂纹九宫板结构。

从表3可以看出，经单、双面复合材料补片修补后，含裂纹九宫板的KI，max 分别降低了48%和89%，裂尖处的振幅分别降低了68%和61%，说明在共振条件下，采用复合材料修补可以有效地降低裂尖处的I型动应力强度因子最大值KI，max 和面外振幅U3，max。原因在于复合材料补片的主刚度方向垂直于裂纹开裂方向，而该方向的弹性模量是裂纹结构的2倍。振动载荷导致的I型SIF（KI，max）比I型和III型SIF（KII，max和KIII，max）大得多，因此，振动条件下，KII，max和KIII，max忽略不计。比较单、双面复合材料补片修补效果发现，采用复合材料双面修补后，裂尖处的KI，max最小，原因在于双面复合材料修补比单面补片修补具有更强的载荷承载能力。采用双面复合材料修补后，结构的一阶模态频率较低，原因是在一阶模态振型时，双面修补降低了结构的弯曲刚度。当采用单、双面修补后，结构的附加重量比分别是1.2%和2.4%，考虑到附加重量和振动响应，在接下来的分析中，将采用复合材料补片单面修补的方式对含中心穿透裂纹九宫板结构进行修补。

3.2" 补片面积的影响

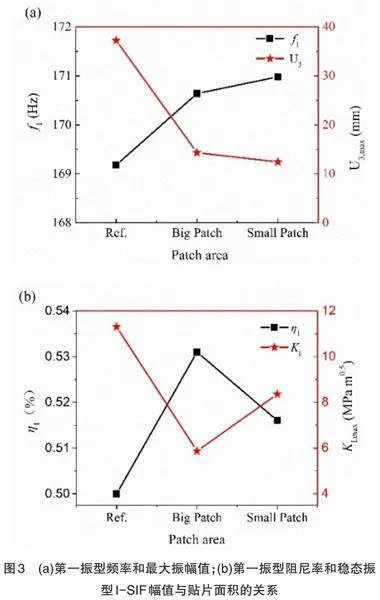
为了研究复合材料补片面积大小对抑振修补效果的影响，本节采用厚度均为0.8mm，面积不同的两个椭圆形单向复合材料补片分别粘贴在九宫板结构与筋条异侧面板的裂纹正上方。小面积补片的尺寸为：2w=168mm，2h=110mm；大面积补片的尺寸为：2w=300mm，2h=200mm。采用大小复合材料补片后，附加质量比分别为0.4%和1.2%，对结构振动修补性能的影响结果如图3所示。

如图3（a）所示，当采用大、小两种面积的单向碳纤维/环氧复合材料补片修补含裂纹九宫板结构后的模态频率均有所增大，增大幅值约为1%；稳态共振时的最大幅值U3，max 降低明显，分别降低61%和67%，振幅差异的主要原因是相比大面积补片，采用小面积的复合材料补片修补结构后的一阶模态频率更远离含裂纹九宫板结构的一阶模态频率。在共振区域，当结构的频率离外界激励频率越远时，结构的振动幅值越小；当激励频率越接近结构的模态频率，结构的振幅越明显。未修补的九宫板结构及采用大、小面积复合材料补片修补后的九宫板结构的一阶模态损耗因子和I型应力强度因子最大值KI，max 如图3（b）所示。

经大、小复合材料补片修补后结构的一阶模态损耗因子η1分别增加了6%和3%，原因是大面积复合材料补片具有更好的阻尼耗散能力；KI，max降低幅值分别达到48%和26%，原因是大面积的复合材料补片具有更好的载荷承载能力。采用大、小面积复合材料补片，附加质量分别增加了1.23%和1.16%。综上而言，当采用大面积的复合材料补片后，结构的附加质量和模态频率改变量很小，但I型SIF和面外振幅降低更加明显。因此，采用较大补片具有更好的抑振修补效果。在下文的分析中，补片的尺寸均采用此节中“大面积补片”的尺寸。

3.3" 补片厚度的影响

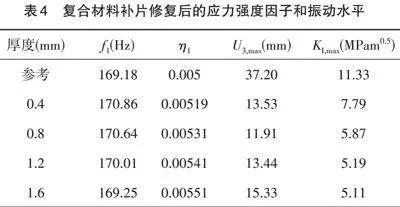
粘贴适当厚度的复合材料补片可以有效抑制裂纹的扩展并降低结构的振动水平，然而不当的复合材料修补可能起不到修补抑振的效果，甚至加剧结构的局部振动、加速裂纹扩展使得损伤结构更快地失效。因而本节通过改变补片厚度，研究其对含中心穿透裂纹九宫板结构的一阶模态频率、一阶模态阻尼、裂尖I型应力强度因子最大值KI，max和面外振幅U3，max的影响，具体结果如表4所示。采用的补片形状为上一节中较大的椭圆形补片，即其2w=300mm，2h=200mm，补片厚度分别选取0.4mm、0.8mm、1.2mm、1.6mm。参考为未修补的损伤九宫板结构。

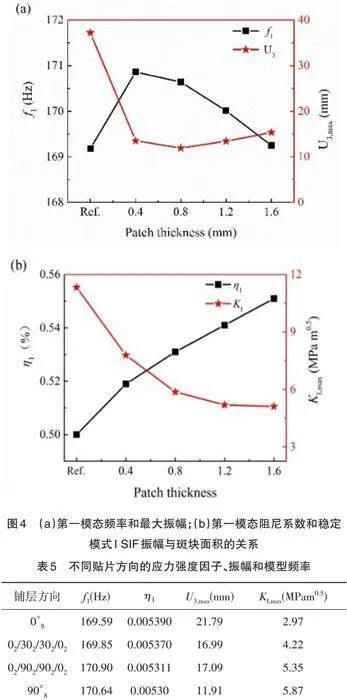
随着补片厚度增加，九宫板结构一阶模态频率变化小于1%，裂尖处的面外振幅U3，max和I型应力强度因子最大值KI，max也随之发生变化，图4更直观地说明补片厚度对含中心裂纹九宫板结构修补效果的影响。随着补片厚度的增大，结构的一阶模态频率f1先增大然后降低，面外振幅U3，max先减小后增大，如图4（a）所示。

从图4（b）可以看出，当补片厚度从0增大到1.6mm，结构一阶模态损耗因子随之增大，而KI，max先急剧下降然后缓慢降低，因此较厚的补片有更好的修补和抑振的效果。结合表4可知，当复合材料补片厚度为0.4mm时，结构的附加质量比为0.62%，裂尖处的KI，max值较未修补时的KI，max值降低了31%；当补片厚度为0.8mm时，结构的附加质量比为1.23%，裂尖处的KI，max值较未修补时的KI，max值降低了48%；之后，随着补片厚度的继续增大，其裂尖处的KI，max缓慢降低，且其模态频率也逐渐降低，当补片厚度为1.6mm时，结构的附加质量比为2.46%，裂尖处的KI，max值降低了55%。综上所述，当补片厚度为0.8mm时，修补时的附加重量比适当而补强效果较好，因此在下文的分析中保持补片厚度为0.8mm。

3.4" 补片铺层方向的影响

复合材料补片在提高部件的强度和寿命方面发挥着重要作用。铺层方向是影响复合材料力学性能的一个重要因素。当复合材料补片厚度保持不变时，材料的铺层方向是影响修补结构力学性能的重要因素。本节采用椭圆形的复合材料补片尺寸为：2w=300mm，2h=200mm，补片厚度为0.8mm，研究四种铺层方式：0°8、90°8、02/902/902/02、02/302/302/02，对结构一阶模态频率、模态损耗因子、裂尖处KI，max 和面外振幅U3，max等修补效果的影响，有限元模拟计算结果如表5所示。

当复合材料补片位置、形状和厚度相同但铺层角度不同时，修补后结构的一阶模态频率改变不足1%，而裂尖处KI，max和面外振幅U3，max差异较大。结果说明：复合材料补片的铺层方向对裂纹区域的应力强度因子和位移场分布具有重要影响，而对整个结构的刚度影响不大。当铺层方向为0°8时，即纤维方向平行于裂纹方向时，起补强作用的是纤维截面强度、基体强度以及纤维与基体的界面强度，其值比纤维轴向强度低得多，因而其补强作用最小，一阶模态频率最低，但面外振幅较其他铺层方向大。原因是振动载荷作用下，裂纹类型为I型，当铺层方向为0°时，修补后结构的模态频率和未修补结构的频率最接近，因而其振幅最大。当补片的偏转角度02/302/302/02变化到02/902/902/02时，结构的一阶模态频率增大，九宫板结构裂尖处的KI，max增加了21%。其原因是随着偏转角度的变化，在裂纹止裂方向复合材料补片的有效弹性模量有所降低。综上，复合材料修补的补强效果与铺层方向密切相关，而铺层方向依赖于结构振动方向和裂纹方向。当结构具有最大的阻尼损耗因子，同时具有最小的KI，max，提高结构阻尼是降低结构共振时的SIF的一种重要方法。因此很有必要研究阻尼性能对结构SIF的影响。

3.5" 阻尼的影响

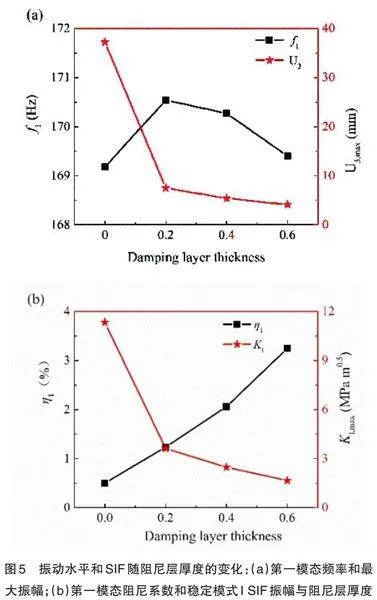
在共振环境下，结构的阻尼性能对结构振动疲劳寿命具有重要影响，特别是在损伤金属结构修补过程中，阻尼的作用更是不可忽略。当补片有较高阻尼性能时，它可以有效降低其共振振幅，进而达到降低结构的应力水平，提高其寿命的目的。虽然复合材料阻尼值比一般的金属材料要高，但因复合材料补片附加质量很小，对整个修复结构的阻尼贡献有限。因而，考虑在复合材料补片层间加入阻尼性能优良的阻尼层片，即将复合材料补片调整为“复合材料层/阻尼层/复合材料层”三明治形式的补片，其中上下两面的复合材料层厚度一样。该三明治形式补片既可以补强又可以提高结构的阻尼，从而达到抑振的效果。为了研究该三明治形式补片中阻尼对含裂纹九宫板结构的抑振补强效果，补片总厚度保持为0.8mm，单向复合材料补片0°方向垂直于裂纹方向，调整阻尼层厚度分别为0.2mm、0.4mm、0.6mm，相应的复合材料层层厚分别为0.3mm、0.2mm、0.1mm。补片中依然采用碳纤维/环氧复合材料，其参数如表2所示，型号为3M112D的粘弹性材料作为阻尼层片，其性能参数如表1所示。相应复合材料补片的附加质量与含裂纹九宫板结构质量比分别是1.11%、0.99%和0.87%。通过有限元模拟得到不同补片布置形式后九宫板结构的一阶模态模态频率、模态阻尼、裂尖处的KI，max和U3，max，具体如图5所示。

从图5可以看出，在复合材料补片中间插入阻尼材料后，随着阻尼材料用量的增大，结构的一阶模态频率先增加后降低，变化幅值小于1%；模态阻尼η1显著增大；结构的KI，max和U3，max显著降低。当插入的阻尼层厚度为0.2mm、0.4mm和0.6mm时，修补后结构的模态阻尼分别增加了约2.5倍、3.1倍和5.5倍；KI，max分别降低了68%、78%和85%；U3，max分别降低了80%、86%和89%。

综上所述，当阻尼层厚度为0.6mm时，结构修补抑振效果最佳。因此，在复合材料补片中插入阻尼片可以显著地提高含裂纹加筋板的阻尼因子并显著降低结构的KI，max，这是一种修补含裂纹结构的有效方法。

4 结 论

本文采用三维有限元软件模拟研究在共振条件下，不同复合材料补片参数对修复含裂纹九宫板在共振状态下的修复效果和抑振水平。结果表明：

（1）当采用复合材料补片单面和双面修补结构时，结构的修补和抑振效果都较为明显。从附加质量和操作的便宜性考虑，将补片布置在筋条的异侧即单面修补效果更佳。

（2）相较于小补片修补，黏贴较大面积补片后结构的附加质量和模态频率改变量也很小，但其裂尖应力水平和面外振幅的降幅更为明显，因此，采用较大补片具有更好的抑振修补效果。

（3）采用0.8mm厚的复合材料补片修补后，结构裂尖的KI，max和面外振幅分别降低了61%和48%，修复效果最佳。

（4）当复合材料补片铺层的偏转角度从0°8到90°8变化时，结构的一阶模态频率缓慢增大，其裂尖处KI，max和面外振幅急剧降低。即补片纤维铺层方向垂直于裂纹方向时，对结构的修补效果最好。

（5）在复合材料补片中间插入阻尼层，随着阻尼厚度增大，结构阻尼性能明显提高。当插入厚度为0.6mm的阻尼片时，结构抑振效果最好。

综上所述，当补片位置处于九宫板筋条异侧，采用较大面积补片，补片厚度为0.8mm，复合材料补片铺层方向垂直于裂纹方向时，对九宫板结构的修补效果最好。同时，在补片中间插入阻尼层，具有显著的修补和抑振效果。

参考文献：

［1］GU L，KASAVAJHALA A，ZHAO S.Finite element analysis of cracks in aging aircraft structures with bonded com-posite-patch repairs［J］.Engineering，2011，42（3）：505-510.

［2］BAKER A A.Repair efficiency in fatigue-cracked aluminium components reinforced with boron/epoxy patches［J］.Fatigue amp; Fracture of Engineering Materials amp; Structures，1993，16（7）：753-765.

［3］OKAFOR A C，SINGH N，ENEMUOH U E，RAO S V.Design，analysis and performance of adhesively bonded composite patch repair of cracked aluminum aircraft panels［J］.Composite Structures，2005，71（2）：258-270.

［4］BELLALI M A，SERIER B，MOKHTARI M，CAMPILHO R S G，LEBON F，FEKIRINI H.XFEM and CZM modeling to predict the repair damage by composite patch of aircraft structures：Debonding parameters［J］.Composite Structures， 2021，266：113805.

［5］RATURI A，JOSHI A，RAWAT P.Advanced composite repair technology for aerospace，marine，and automobile applications［A］.in Sustainable Biopolymer Composites，D Verma，et al［C］.Woodhead Publishing，2022：265-279.

［6］BOUIADJRA B B，BOUANANI M F，ALBEDAH A，BENYAHIA F，ES-SAHEB M.Comparison between rectangular and trapezoidal bonded composite repairs in aircraft structures：A numerical analysis［J］.Materials amp; Design，2011，32（6）：3161-3166.

［7］RACHID M，SERIER B，BACHIR B B，et al.Numerical analysis of the patch shape effects on the performances of bonded composite repair in aircraft structures［J］.Engineering，2012，43（2）：391-397.

［8］TONG L，LI S，XIONG G.Material parameter modeling and solution technique using birth–death element for notched metallic panel repaired with bonded composite patch［J］.Chinese Journal of Aeronautics，2014，27（2）：445-452.

［9］MAKWANA A H，VYAS N，BAROT R S.Numerical investigation of composite patch repair of inclined cracked panel using XFEM［J］.Materials Today：Proceedings，2021，45：5128-5133.

［10］TING T，JONES R，CHIU W，et al Composite repairs to rib stiffened panels［J］.Composite Structures，1999，47（1）： 737-743.

［11］JONES R，WHITTINGHAM B， MARSHALL I.Bonded repairs to rib stiffened wing skins［J］.Composite Structures，2002，57（1）：453-458.

［12］MAKWANA A H，VYAS N，BAROT R S.Numerical investigation of composite patch repair of inclined cracked panel using XFEM［J］.Materials Today：Proceedings，2021，（45）：5128-5133.

［13］JONES R，CHIU W K，MARSHALL I.Weight functions for composite repairs to stiffened panels［J］.Engineering Failure Analysis，2004，11（1）：49-78.

［14］FREDELL R S.Damage tolerant repair techniques for pressurized aircraft fuselages［D］.Delft University of Technology，1994.

［15］JONES R.A scientific evaluation of the approximate 2D theories for composite repairs to cracked metallic components［J］.Composite Structures，2009，87（2）：151-160.

［16］ROGERS，L C，SEARLE，I R，IKEGAMI R，et al. Durability patch：application of passive damping to high-cycle fatigue cracking on aircraft［J］.Proceedings of SPIE - The International Society for Optical Engineering，1997，3045：214-223.

［17］IKEGAMI R，HAUGSE E，TREGO A，et al. Structural Technology and Analysis Program （STAP） Delivery Order 0004：Durability Patch［R］.DTIC Document，2001.

［18］LIU S，LI Y，DENG Q，et al.Topological optimization design of 3×3 grid stiffened panel with additional damping layers based on evolutionary structural optimization［J］.Journal of vibration and shock，2016，35（22）：197-203.

［19］LIU S，LI Y，XUE P，et al.Effect of crack parameters and stiffener layout on dynamic stress intensity factor of 3×3 grid stiffened panel［J］.Acta Aeronautica et Astronautica Sinica，2018，39：221423.

［20］WAHAB，M A.Dynamics and vibration： an introduction［Z］.John Wileyamp;Sons Ltd，2007.

［21］CHARABORTY B，RATNA D.Chapter 1 - Fundamentals of vibration damping，in Polymers for Vibration Damping Applications［M］.B C" Chakraborty and D Ratna，Editors.Elsevier，2020：1-42.

［22］GALENNE E，ANDRIEUX S，RATIER L.A modal approach to linear fracture mechanics for dynamic loading at low frequency［J］. Journal of Sound and Vibration，2007，299（1）：283-297.

［23］MARIOLI-RIGA Z X D，VRETTOS C.Standard analysis method for the stress analysis of repaired aircraft structures with the method of composite patch repair［J］.Applied Composite Materials，2004，11（4）：191-203.

［24］HAN Q，WANG Y，YIN Y，WANG D.Determination of stress intensity factor for mode I fatigue crack based on finite element analysis［J］.Engineering Fracture Mechanics，2015，138：118-126.

责任编校：裴媛慧，陈 强

Damping Effect of Bonded Composite Repair for Vibration Suppression of Cracked Metallic Panels

LIU Shuangyan， ZHU Bingbing

（School of Aero Engine，Zhengzhou University of Aeronautics，Zhengzhou 450046，China）

Abstract：This paper investigates the damping effect of bonded composite repair for vibration suppression of cracked metallic panels.Influence of patch geometric parameters on the vibration level and repair efficiency is examined. Vibration level is characterized by the first modal frequency，modal damping loss factor， and the vibration amplitude out of a plane at the crack tip.The repair efficiency is evaluated by the amplitude of stress intensity factor.Results reveal that after a repair the stress intensity factors exhibit an asymptotic behaviour as the modal damping loss factor increases，especially when inserting damping materials into the composite patch.

Key words：patch；repair parameters;vibration suppression;cracked Metallic Panels

基金项目：河南省科技攻关项目（232102240037，242102241026，232102220028，242102110203）；郑州航空工业管理学院科研团" " " " " " " " " " "队支持计划专项（23ZHTD01010）

作者简介：刘双燕，河南南阳人，博士，讲师，研究方向为结构振动控制与振动能量收集。