不稳定地月循环轨道的混沌控制方法

摘 要：针对现有的地月循环轨道稳定控制方法仅对少数轨道有效的缺点，本文提出了一种圆型限制性三体问题下不稳定地月循环轨道的混沌控制方法。首先在循环轨道上选择候选不动点及其对应的庞加莱截面图；然后通过混沌控制方法将轨道在庞加莱截面图上的投影点移动到不动点的稳定方向上；再计算轨道被控制后的目标点和轨道投影点到不动点之间偏差距离的比例，依次对比例最小的候选不动点进行筛选；最后根据所选择的不动点确定庞加莱截面图，计算控制脉冲量，对循环轨道进行稳定控制。仿真结果表明，本文所提出的方法适用于各种类型的地月循环轨道，相比现有方法至少节省了66%的能耗，能够使循环轨道长时间趋于稳定。

关键词：圆型限制性三体问题；地月循环轨道；混沌控制；庞加莱截面图；控制脉冲

中图分类号：V412.4" " " " " " " 文献标识码：A" " " " " 文章编号：1007 - 9734 （2024） 02 - 0014 - 06

0 引 言

地月循环轨道是三体问题下往返于地球与月球之间的周期轨道。该轨道能够兼顾地球和月球的探测，并且能够被重复利用。运行在循环轨道上的探测器不需要轨道机动或只需进行少量轨道机动即可运载人员和物资往返于地月之间，并且不需要消耗大量能量重新将星探测器从地面运送到星际转移入轨点。因此，循环轨道可以用于完成长期的、持续的月球探测任务，是一种有研究价值和发展潜力的轨道转移方案。

1957年，Egorov［1］最早发现了地月循环轨道。随后，研究人员找到了更多的轨道［2-4］，其中最有实践价值的是1963年Arenstorf［5-6］发现的被命名为Arenstorf的两条轨道，后来被用于阿波罗计划。2013年，Casoliva［7］等将地月循环轨道分为与月球公转轨道存在共振关系的地月高能共振循环轨道和经过月球时会绕月球运转数圈的地月低能循环轨道。学者们分别对这两种循环轨道的构造和计算方法进行了研究［8-10］。2017年，美国正式批准了阿尔忒弥斯计划，旨在重新夺回月球的探索领域，开发月球空间站。地月循环轨道作为周期往返于地月之间的轨道，是一种重要的用于建立月球空间站的轨道类型［11］。然而，大部分地月循环轨道属于不稳定周期轨道，小扰动会使探测器偏离轨道而导致探测任务失败，需要对其进行稳定控制。

不稳定地月循环轨道位于三体系统的混沌区域内，混沌轨道对初始状态具有高度敏感的特性。一方面，由于小扰动的指数放大会导致探测器偏离固有的轨迹；另一方面，通过小的控制量也能够对偏离轨道进行调整使其趋向于固有周期轨迹。目前将混沌控制理论用于探测器轨道的研究还处于起步阶段。1990年，美国马里兰大学的物理学家Ott、Grebogi和Yorke［12］首先提出了著名的OGY控制方法，开辟了混沌控制的先河。OGY方法利用了混沌运动的遍历性及对微小扰动的敏感性，将小扰动控制量加进混沌系统，把轨迹控制在不稳定周期轨道某一不动点的稳定流形上，实现将轨迹稳定于不稳定周期轨道的目的。1995年，Bollt等［13］首次将混沌控制应用于地月轨道转移的研究中，通过混沌运动方法实现了地月轨道转移，比霍曼转移方法节省了38%的燃料。一些学者改进了Bollt的方法，缩短了地月转移时间［14-15］。2006年，Leiva［9］针对地月低能循环轨道，通过周期轨道不动点的稳定方向设计了一种混沌控制方法，找到了一条控制后可长时间保持稳定的轨道，以10m/s的脉冲量使循环轨道稳定330个周期。2019年，文献［10］进一步研究了Bollt的方法，以1.5m/s的脉冲量使该循环轨道稳定500个周期。然而，现有方法仅以一条地月低能循环轨道为例来验证稳定控制效果，对其他轨道，尤其是地月高能共振循环轨道的控制效果并不理想。

现有混沌控制方法存在的问题是：地月循环轨道的稳定控制是通过预先设置的同一个庞加莱截面图上的不动点来实现的，不能保证最好的控制效果，导致控制方法仅对个别轨道有效。本文提出了一种混沌控制方法，根据每一条轨道状态计算控制效果最好的不动点，能够使任意不稳定地月循环轨道保持稳定。该方法在循环轨道上选择合适的不动点，条件是轨道经小脉冲量控制后在庞加莱截面图上的投影点距离不动点尽可能近；利用不动点确定庞加莱截面图，轨道每运行一个周期，通过混沌控制方法在庞加莱截面图上计算控制脉冲，将轨道状态量移动至不动点的稳定方向上，从而使不稳定地月循环轨道长时间趋于稳定。

1 动力学模型

考虑地月圆型限制性三体问题（Circular Restricted Three-Body Problem，CRTBP），质量可以忽略的探测器在地球和月球两个主天体的引力作用下的运动，其中主天体绕其公共质心做匀速圆周运动[16]。归一化地球质量[m1]和月球质量[m2]之和为单位质量（[m1m2=0.0123]），则：

[m1=1-μm2=μ]" " " " " " " " " " " " " " " " " " " " " " " " " " " （1）

其中，[μ]为两主天体的质量比常数（地月系统中，[μ=0.01215]）。使用假设地月主天体静止的质心旋转坐标系，地球和月球分别被固定于[-μ，0]和[1-μ，0]，用[x，y]，[x，y]分别表示探测器的位置和速度，探测器的运动学方程为：

[x-2y=∂Ω∂xy+2x=∂Ω∂y]" " " " " " " " " " " " " " " " " " " " " " " " " "（2）

其中，[Ω]为旋转坐标系下的等效势能：

[Ω（x，y）=12x2+y2+1-μr1+μr2]" " " " " " " " "（3）

设矢量[r1]，[r2]为探测器到两个主天体的距离，有：

[r21=x+μ2+y2r22=x-1+μ2+y2 ]" " " " " " " " " " " " " " " " " （4）

CRTBP系统中，存在雅可比积分如下：

C=2[Ω-（x2+y2]）" " " " " " " " " " " " " " " " " " " " " " " （5）

在地月三体系统中，单位长度为地月之间的距离，[L=3.844×105km]，单位时间为[T=104h]，单位速度为[V=1024ms]。

2 地月循环轨道及稳定性判据

地月CRTBP内存在很多往返于地月之间的循环轨道，探测器一旦处于循环轨道上，在没有外力影响的情况下能够一直在这些轨道上运行而完成长期的地月探测任务。然而，当地月循环轨道不稳定时，一方面，由于不稳定周期轨道容易受到小扰动的干扰从而使其轨迹偏离周期轨道；另一方面由于现有积分运算工具不能达到足够高的精度，所以计算出的轨道初始值与实际值存在一定的差距，长时间积分后的轨迹也会与原先轨道产生一定的偏差。

2.1" 地月循环轨道及分类

地月循环轨道是周期性往返于地球与月球之间的一类周期轨道。用探测器在质心旋转坐标系下的位置矢量[x，y]和速度矢量[x，y]组成的无量纲状态量[x，y，x，yT]表示t时刻地月CRTBP动力学方程的一个解，地月循环轨道在周期内满足：

[x，y，x，yt=0=x，y，x，yt=T]" " " " " " " " " " " " "（6）

地月循环轨道按照轨道能量可以分为地月高能共振循环轨道和地月低能循环轨道，如图1所示。图1（a）、图1（b）为地月高能共振循环轨道，轨道能量较高，其运动轨迹的近地点半径较小，经过月球附近时不会围绕月球运转，与地月系统公转存在一定共振关系；图1（c）、图1（d）为地月低能循环轨道，轨道能量较低，其运动轨迹的近地点半径较大，经过月球时会围绕月球运转数圈，与地月系统公转不存在共振关系。

2.2" 循环轨道的稳定性判据

状态转移矩阵揭示了初始状态无限小的摄动随时间传播引起的终端状态的发散程度，即终端状态对初始状态的敏感程度。在地月CRTBP中，令[X=x，y，x，yT]为探测器状态，[Φt，t0]为非线性系统线性化方程的状态转移矩阵。给定初始条件[X0=X0]，[Φt0，t0=I4]，状态转移矩阵的数值解可通过式（7）进行计算：

[ddtXt=fXtΦt，t0=AtΦt，t0]" " " " " " " " " " " " " " " " " （7）

其中

[A（t）=00100001ΩxxΩxy02ΩyxΩyy-20]" " " " " " " " " " " " " " " "（8）

循环轨道作为一类特殊的周期轨道，其稳定性通常由单值矩阵判断。单值矩阵是周期轨道上选择一个初始状态量，经过一个周期T后的特殊的状态转移矩阵，即：

[M=ΦT，0=∂XT∂X0]" " " " " " " " " " " " " " " " " " （9）

其中，[X0]表示探测器在周期轨道上的初始状态量，[XT]表示探测器从[X0]出发运动一个周期后的状态量。通过分析周期轨道对应的单值矩阵的特征值，能够判断周期轨道的稳定性。平面周期轨道的单值矩阵存在两个为实数“1”的特征值和两个互为倒数的特征值。设互为倒数的特征值为[λ]和[1λ]，定义周期轨道的稳定性判据为：

[s=λ+1λ]" " " " " " " " " " " " " " " " " " " " " " " " " " "（10）

周期轨道稳定性与特征值的关系为：

（1）当特征值为共轭复数，即[λ=cosθ±isinθ]时，[s≤2]，周期轨道稳定；

（2）当特征值为互为倒数的实数，即[λgt;1]，[1λlt;1]时，[sgt;2]，周期轨道不稳定。

对于不稳定周期轨道，[λgt;1]时对应的特征向量方向为周期轨道的不稳定方向，轨迹在不稳定方向的偏差会以指数形式放大；[1λlt;1]时对应的特征向量方向为周期轨道的稳定方向，轨迹在稳定方向的偏差会以指数形式缩小。

3 地月循环轨道的稳定性控制

不稳定地月循环轨道位于地月CRTBP的混沌区域内，会因小扰动或者数值解精度的误差而偏离固有轨迹，原因是混沌运动对小扰动或者误差在周期轨道不稳定方向上的指数放大。另一方面，利用周期轨道稳定方向上的小控制量也会使偏离轨迹与周期轨道之间的偏差指数缩小进而趋向于周期轨道。本节提出了一种混沌控制方法，在庞加莱截面图上选择合适的周期轨道不动点，通过小脉冲量将轨道状态量移动至不动点的稳定方向上，使不稳定地月循环轨道能够长时间趋于稳定。

3.1" 不动点的选择

地月循环轨道上任意一点都可作为不动点，通过单值矩阵可计算出远离周期轨道的不稳定方向和靠近周期轨道的稳定方向。选择合适的不动点，利用其稳定方向对轨道进行混沌控制，能够在能量尽可能小的情况下，实现将不稳定循环轨道保持稳定的目的。

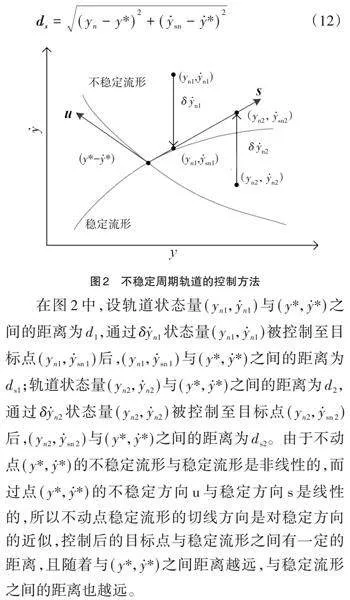
在地月循环轨道上，设不动点的状态量为[X*=x*，y*，x*，y*T]，选择[x=x*]的庞加莱截面，投影方向与[x*]方向一致，则该不动点在庞加莱[y，y]截面图上的投影点为[y*，y*]。地月循环轨道每次穿过庞加莱截面后，在庞加莱截面图上的投影点依次为[y1，y1]，[y2，y2]，…，[yn，yn]。由于循环轨道不稳定，轨道投影点[yn，yn]会偏离不动点在庞加莱截面图上的投影点[y*，y*]。以不动点为初始值可通过单值矩阵计算出不稳定特征值[λu]及特征向量[eu=xus，yus，xus，yusT]，稳定特征值[λs]及特征向量[es=xes，yes，xes，yesT]。如图2，在庞加莱[y，y]截面图上，不动点的不稳定方向[u=yu，yu]与不稳定流形相切；不动点的稳定方向[s=ys，ys]与稳定流形相切。

当地月循环轨道偏离不动点时，设在庞加莱[y，y]截面图上轨道状态量的投影点[yn，yn]与不动点投影点[y*，y*]之间的距离为：

[d=yn-y*2+yn-y*2]" " " " " " " " " " " " （11）

使循环轨道趋于稳定的方法是通过施加控制脉冲将[yn，yn]移动到[y*，y*]的稳定方向上。由于所施加的控制脉冲只改变状态点的速度，不改变状态点的位置，所以控制脉冲在庞加莱[y，y]截面图上的投影[δy]与[y]轴垂直。设[yn，yn]被移动到[y*，y*]稳定方向上后的投影点为[yn，ysn]，[y*，y*]与[yn，ysn]之间的距离为：

[ds=yn-y*2+ysn-y*2]" " " " " " " " " " " （12）

在图2中，设轨道状态量[yn1，yn1]与[y*，y*]之间的距离为[d1]，通过[δyn1]状态量[yn1，yn1]被控制至目标点[yn1，ysn1]后，[yn1，ysn1]与[y*，y*]之间的距离为[ds1]；轨道状态量[yn2，yn2]与[y*，y*]之间的距离为[d2]，通过[δyn2]状态量[yn2，yn2]被控制至目标点[yn2，ysn2]后，[yn2，ysn2]与[y*，y*]之间的距离为[ds2]。由于不动点[y*，y*]的不稳定流形与稳定流形是非线性的，而过点[y*，y*]的不稳定方向[u]与稳定方向[s]是线性的，所以不动点稳定流形的切线方向是对稳定方向的近似，控制后的目标点与稳定流形之间有一定的距离，且随着与[y*，y*]之间距离越远，与稳定流形之间的距离也越远。

在图2中，轨道状态量[yn1，yn1]和[yn2，yn2]与不动点[y*，y*]之间的距离相等，即[d1=d2]，尽管控制脉冲[δyn1=δyn2]，但是将状态量移动到稳定方向[s]后，[ds1lt;ds2]，所以[yn1，ysn1]更接近稳定流形，轨道通过控制脉冲[δyn1]将状态量[yn1，ysn1]移动到[yn1，ysn1]能够得到更好的稳定控制效果。因此，在周期轨道上选择不动点[y*，y*]时，需要考虑偏离轨道在不动点稳定方向的目标点，使其距离不动点的距离尽可能小，以达到更好的控制效果。

3.2" 控制脉冲量的计算

通过小脉冲量，可将轨道调整至周期轨道上的选定状态点的稳定流形上，使不稳定循环轨道趋于稳定。在庞加莱[y，y]截面上，设不动点[y*，y*]的稳定方向的特征向量为[s=sy，sy]，轨道的投影点[yn，yn]通过脉冲量在[y]方向的分量[δyn]后被控制在[y*，y*]的稳定方向上，则满足：

[yn，yn+δyn=y*，y*+αs]" " " " " " " " " " " " "（13）

根据式（13），可计算出[δyn]的值为：

[δyn=sysyyn-y*-yn-y*]" " " " " " " " " " " " （14）

由于轨道被小脉冲量控制后需要保持能量相等，那么满足：

[xn+δxn2+yn+δyn2=x2n+y2n]" " " " " " " " （15）

根据式（15），可计算出[δx]的值为：

[-xn+xn1-2ynδyn+δyn2x2n，xngt;0-xn-xn1-2ynδyn+δyn2x2n，xnlt;0]" " "（16）

所以，对轨道施加的控制脉冲量的大小为：

[Δvn=δxn2+δyn2]" " " " " " " " " " " " " " " " "（17）

施加脉冲后，轨道投影点[yn，yn]被移动至地月循环轨道不动点[y*，y*]的稳定方向上后，得到目标点[yn，ysn]，当[yn，ysn]距离[y*，y*]较近时，正向时间积分后可使轨道逐渐靠近不动点[y*，y*]从而使不稳定地月循环轨道趋于稳定。

3.3" 控制算法流程

本文对不稳定地月循环轨道进行稳定控制的方法如图3所示。具体步骤如下。

第一步：在地月循环轨道上选择等时间间隔的状态点作为周期轨道的不动点[X*][=x*，y*，x*，y*T]，根据不动点的状态量确定庞加莱[y，y]截面图，[X*]在庞加莱截面图上的投影点为[y*，y*]；

第二步：通过循环轨道上每一个不动点的单值矩阵计算稳定方向，以不动点作为初始点对地月循环轨道进行正向时间积分，记录循环轨道大约运行一个周期[T]后在庞加莱[y，y]截面图上的第一个投影点[y1，y1]，令[y1，y1]与[y*，y*]之间距离为[d]，将投影点移动到不动点的稳定方向上的目标点[y1，ys1]，令[y1，ys1]与[y*，y*]之间距离为[ds]；

第三步：选择[dsdlt;0.2]的不动点作为候选，将地月循环轨道上每一个不动点所计算出的[dsd]以从小到大的顺序进行排序；

第四步：选择[ds]最小时的不动点作为地月循环轨道的初始点；

第五步：对轨道运行一个周期[T]后在庞加莱[y，y]截面图上的投影点进行控制，计算控制脉冲[δxn，δyn]；

第六步：当轨道的控制脉冲量[Δvn]小于允许的最大脉冲量[Δvmax]时，对轨道状态量进行调整，并使轨道运行至下一周期；否则回到第四步，根据[ds]的排序再次选择不动点，如果所有不动点均不能实现稳定控制则算法对该循环轨道不适用；

第七步：当循环轨道能够稳定运行周期数小于N时，回到第五步，继续对轨道进行稳定控制；否则，完成循环轨道的稳定控制，算法成功。

4 数值仿真分析

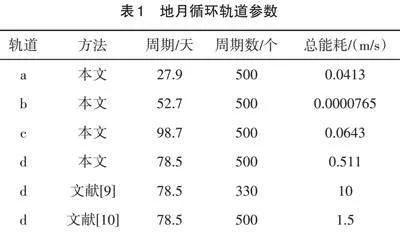
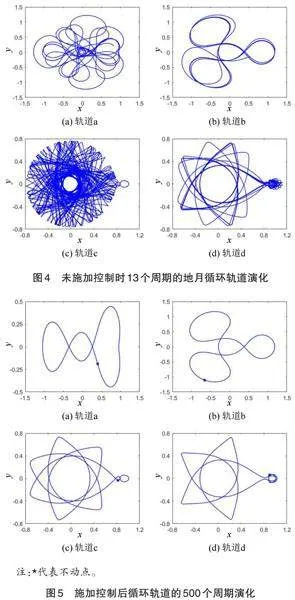
图1中的4条地月共振循环轨道均为不稳定周期轨道，图4为在未施加控制的情况下，轨道a，轨道b，轨道c和轨道d经过13个周期后偏离周期轨道的轨迹图。利用本文方法对这4条地月循环轨道进行混沌控制，设每次施加控制脉冲时允许的最大脉冲量[Δvmax=10-5]，稳定周期数[N=500]。施加控制后的轨道如图5所示，*代表轨道的不动点，根据不动点的状态量可确定庞加莱[y，y]截面图，将轨道每次在庞加莱截面图上的投影通过小脉冲量移动到不动点的稳定方向上，使不稳定地月循环轨道长时间趋于稳定，轨道参数如表1所示。

将本文方法与现有的方法进行对比，现有方法仅针对一条地月低能循环轨道——轨道d进行稳定控制，而本文方法对地月低能循环轨道和地月高能共振循环轨道都有很好的稳定控制效果。针对轨道d，文献［9］将轨道稳定控制330个周期的总能耗为10m/s，文献［10］将轨道稳定控制500个周期的总能耗为1.5m/s，本文将轨道稳定控制500个周期的总能耗仅为0.518m/s，较文献［9］节省了95%的能耗，较文献［10］节省了66%的能耗，通过更少的能耗对轨道实现混沌控制，使循环轨道长时间保持稳定。

表1 地月循环轨道参数

[轨道 方法 周期/天 周期数/个 总能耗/（m/s） a 本文 27.9 500 0.0413 b 本文 52.7 500 0.0000765 c 本文 98.7 500 0.0643 d 本文 78.5 500 0.511 d 文献[9] 78.5 330 10 d 文献[10] 78.5 500 1.5 ]

5 结 论

本文提出了一种不稳定地月循环轨道的混沌控制方法，该方法能够计算循环轨道上控制效果最好的不动点，根据不动点状态量建立庞加莱截面图，将轨道在庞加莱截面图上的投影点移动到不动点的稳定方向上，使不稳定地月循环轨道长时间趋于稳定。本文提出的方法能够通过非常小的控制脉冲量，使任何类型的不稳定地月循环轨道长期保持稳定，不仅适用于地月低能循环轨道，也适用于地月高能共振循环轨道。

参考文献：

［1］EGOROV，V A.Certain problems on moon flight dynamics［J］.The Russian Literature of Satellites，Part I，1958：115-175.

［2］MESSAGE，P J.The search for asymmetric periodic orbits in the restricted problem of three bodies［J］.The Astronomical Journal， 1958， 63：443.

［3］NEWTON R R. Periodic orbits of a planetoid passing close to two gravitating masses［J］.Smithsonian Contribution to Astrophysics， 1959， 3（7）： 69 -78.

［4］HUANG S S. Preliminary study of orbits of interest for moon probes ［J］.Astronomical Journal， 1962， 67（5）：304 -310.

［5］ARENSTORF R F. Periodic solutions of the restricted three body problem representing analytic continuations of ke-plerian elliptic motions［J］.American Journal of Mathe-matics， 1963， 85（1）：27 -35.

［6］ARENSTORF R F. Existence of periodic solutions passing near both masses of the restricted three-body problem［J］.AIAA Journal， 1963， 1（1）：238 -240.

［7］CASOLIVA J， MEASE K D，Mondelo J， et al. Families of cycler trajectories in the Earth-Moon system ［C］.AIAA/ AAS Astrodynamics Specialist Conference and Exhibit， 2008.

［8］张文博. 循环飞行方案的轨道设计与优化［D］.北京：北京理工大学， 2015.

［9］LEIVA A M， BRIOZZO C B. Control of chaos and fast periodic transfer orbits in the Earth–Moon CR3BP ［J］. Acta Astronautica， 2006， 58（8）：379-386.

［10］郑越.地月三体系统低能转移轨道设计与控制［D］.西安：西北工业大学， 2019.

［11］彭祺擘， 吕纪远.月球空间站停泊轨道选择分析［J］.宇航学报，2022， 43（2）： 167-172.

［12］OTT E， GREBOGI C， YORKE J A. Controlling chaos ［J］.Physical review letters，1990，（64）：1196-1199.

［13］BOLLT E M，KOSTELICH E J.Optimal targeting of chaos ［J］.Physics Letters A， 1998， 245（5）：399-406.

［14］YANG WANG， BINFENG PAN， YUE ZHENG， et al. ETLBO based optimal targeting to the moon in the PCR3BP chaotic system ［J］.Chaos Solitons amp; Fractals， 2017，105：21-28.

［15］ZHENG Y，PAN B F，TANG S.A hybrid method based on invariant manifold and chaos control for Earth-Moon low-energy transfer ［J］.Acta Astronautica，2019，163：145 -156.

［16］刘林.卫星轨道力学算法［M］.南京：南京大学出版社， 2019.

责任编校：裴媛慧，陈 强

Chaos Control Method for Earth-Moon Cyclers

ZHENG Yue，ZHAO Min

（Xi’an Aeronautical Institute，Xi’an 710077，China）

Abstract：Current methods which stabilize unstable Earth-Moon cyclers are only effective for a few orbits. A chaos control method for unstable Earth-Moon cyclers in the circular restricted three-body problem is proposed in this paper. First， candidate fixed points and their corresponding poincaré map are selected on a cycler. Second， the projection point of the cycler is moved to the stable direction of the fixed point by chaos control method on the poincaré map. Third， the proportion of the deviation distance between the target point and the projected point to the fixed point after the cycler is controlled. Finally， the poincaré map is determined according to the selected fixed point， the control pulse amount is calculated， and the Earth-Moon cycler is stabilized. The numerical results are provided to reveal that the proposed method is suitable for various types of Earth-Moon cyclers， which saves at least 66% energy consumption compared to the existing methods， and can stabilize the cycler for a long time.

Key words：circular restricted three-body problem；Earth-Moon cyclers；chaos control；poincaré map；control impulse

基金项目：陕西省科技计划项目（2021JQ-846）；西安航空学院校级科研基金项目（2020KY0209）

作者简介：郑 越，女，陕西西安人，博士，讲师，主要研究方向为航天器轨道设计及优化。