数形结合思想在小学数学教学中的思考

数形结合思想能够让“数”与“形”之间相互转化，使抽象的知识点变得直观、形象，对学生思维发展、能力提升具有诸多益处。小学阶段是学生夯实基础、开启智慧的重要阶段，教师使用的新方法、新思想对学生的思维发展、综合素质提升都具有重要的促进作用。数和形反映了事物在两个方面的属性，数形结合思想能展现数和形之间一一对应的关系，学生在小学阶段接触数形结合思想，有助于开发思维，提高对数学知识的领悟能力，对将来初中阶段的数学学习具有较大帮助。

一、数形结合思想的核心内涵

数形结合思想是一种通过“数”和“形”之间的对应关系解决实际问题的思想方法，在解决问题时可以让“数”和“形”之间相互转化，使问题的突破口显而易见，从而提高解决问题的效率。数学学科主要的研究对象是现实世界的数量关系和空间形式，“数”和“形”之间本身就是既对立又统一的关系，在一定条件下可以相互转化。在小学阶段的数学教学中，“数”主要指代数式、方程、数量关系式等内容，“形”是指几何图形、统计图表等。

二、数形结合思想对小学数学教学的价值分析

（一）直观解析概念，提高教学效率

在小学阶段，学生对语言文字的理解能力较弱，很难准确记忆数学概念的内容，通过融入数形结合思想，教师可以让抽象的概念以直观、形象的方式呈现出来，用可视化的材料优化教学过程，让学生增强学习欲望，准确理解、记忆数学概念。从认知规律来看，视觉记忆比文字记忆更加深刻，在图形和图像的帮助下，学生可以对专业的数学词汇进行再加工，从另一个角度理解知识点，提高学习效率。例如，在学习负数、分数、比例等内容时，教师就可以结合图形进行讲解，帮助学生存储、消化知识。

（二）引导学生观察，发展逻辑思维

在数形结合思想的帮助下，教师能够引导学生在课堂上对各类图形或图像进行观察，培养学生的观察能力，发展学生的逻辑思维。数学学科的很多知识都是共通的，数和形可以相互转化，在转化的过程中，学生的思维能够得到激发，思考问题的方式也会更加灵活。在低年级阶段，教师可以将数的认识、数的计算和图片结合起来，用实际的物品、图形来表示数，将图形和算式整合起来，引导学生在观察图形的过程中理解数的内涵，在数与形的转化中提高逻辑思维。

（三）解决复杂问题，强化实际应用

数学学习的核心目标在于解决实际问题，在整个学习过程中，解题不仅能够发展学生的数学思维，还能帮助学生积累经验，让学生了解自身的薄弱点，提高后期学习的针对性。因此，教师需要培养学生的解题能力，让学生将数学知识应用到实际生活中。小学阶段的很多数学应用题都比较复杂，有的题缺少直接解题的条件，需要进行演算和推理，有的题条件复杂，需要进行梳理才能建立联系，教师在教学中可以主动引入数形结合思想，使解题思路更加清晰。例如，在小学高年级，教师可以将数形结合思想融入复杂的应用题中，让学生通过画示意图的方法解读应用题中的信息，引导学生思考。

三、数形结合思想在小学数学教学中应用的策略

数形结合思想是小学数学教学的重要思想，也是学生解决数学问题的关键思想，能够有效提高学生解决问题的效率，帮助学生对数学问题进行转化。当前，部分教师尚未充分认识到数形结合思想在课堂教学中的应用价值，无法让学生深入理解知识，存在“数”与“形”分离、数形结合思想融入较少等问题。为此，教师需要深入理解数形结合思想，将数形结合思想融入实践教学中，探索出一系列新的教育策略和方法，帮助学生更好地理解数学知识。

（一）以形助数，剖析数学概念

在小学数学教学中，数学概念的教学是最基础的，只有学生掌握数学概念的内涵，学会灵活应用，才能解决数学问题，不断积累学习经验。在数学概念教学中，教师可以运用数形结合思想，通过“以形助数”的方式，对数学概念进行剖析，让学生从“形”的视角解读、记忆数学概念，提高学习效果。例如，在学习“负数”时，不少学生都难以理解负数的概念，教师就可以运用数形结合思想，结合现实生活案例，让学生认识负数。实际上，负数在现实生活中有很多应用，如在表示气温时，我们用10℃表示零上10℃，用-10℃表示零下10℃；在计算亏损和盈利时，我们用正数表示盈利，用负数表示亏损。为了让学生深入理解负数的概念，教师需要引入数轴，引导学生亲身体验、亲自操作。

在课堂上，教师可以站在讲台上，用尺子测量黑板的长度，找到黑板的中心点，过中心点绘制一条水平线，然后邀请两名学生站在讲台的两侧，靠近黑板，保持不动。接下来，其他同学可以测量这两名同学距中心点的长度，以中心点为参照，确定两名同学的位置。在测量后，教师可以提出，用“0”表示黑板的中心，用+1m表示中心点右边1m的位置，用-1m表示中心点左边1m的位置，引导学生绘制数轴，在数轴上标注两名同学的位置，并说一说这样表示的好处。通过数轴，学生可以清晰、直观地理解正数和负数的意义，认识到负数在生活中的重要性。

在教学中，教师可以运用多媒体设备，现场绘制数轴，用数轴表示每位学生到中心点的距离，同样，将中心点的位置设为“0”点，右边为正数，左边为负数，在数轴上标注每位同学的位置，绘制的数轴如图1所示。

通过多媒体技术，学生能够将图像和数字结合起来，通过图形理解数字的意义，通过数字丰富图像的内涵，使“形”与“数”合二为一，共同促进知识的理解。在课堂上，学生可以完成实地测量、实践操作，体会数轴在表示正数、负数时的优势，深刻认识到负数的概念，明确负数是有实际意义的，是和正数相对的，这样才能全面加深对负数的理解，提高数学思维。在教学中，教师需要站在学生的角度思考问题，了解学生的思维模式，理解学生存在的困惑、质疑，然后再运用“以形助数”的方法，帮助学生解除困惑，让知识一目了然。在实践教学中，“以形助数”是对数形结合思想的应用，这种方法能够降低数学知识的抽象性，帮助学生夯实数学基础。

（二）以数解形，把握抽象特征

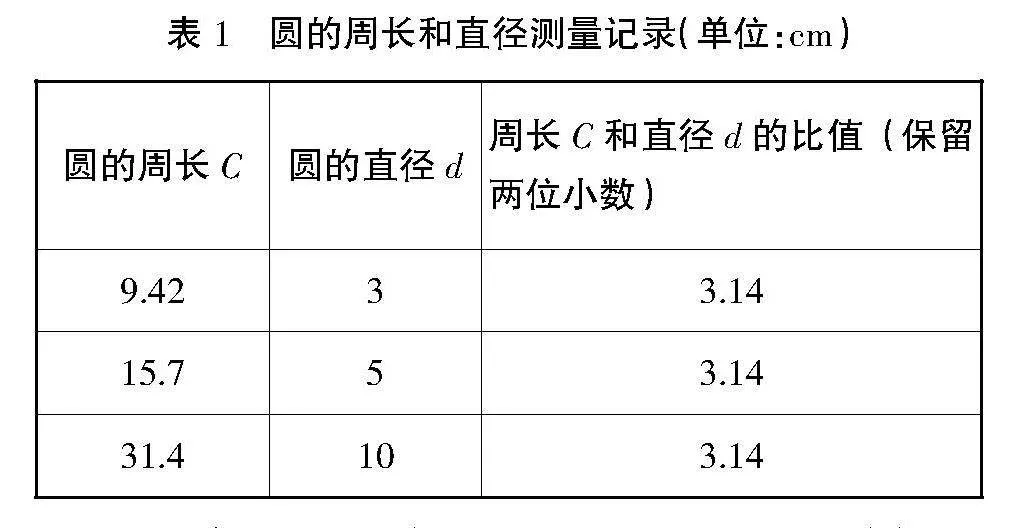
在小学阶段，学生需要初步认识几何图形，了解几何图形的性质和特征，还需要掌握图形的周长和面积的算法，具备几何思维。在学习几何图形时，“以数解形”是一种十分重要的教学方法，如果只开展几何图形的讲解，不结合“数”，学生将难以细致入微地分析图形、理解图形。因此，教师需要具备“以数解形”的意识，提高学生分析图形的能力。例如，在学习“圆”的相关知识时，学生需探索圆的周长和面积的计算方法，了解“圆”中存在的规律，实现探究式学习。这部分知识比较抽象，延伸出的数学问题也比较复杂，很多学生对圆的性质和概念理解不透彻，只能死记硬背，无法用探索的方式学习“圆”的相关知识。在学习“圆的周长”时，学生需要理解圆的周长和圆的直径之间的关系，这种关系是抽象的、不易观察的，此时就要用到“以数解形”的思想。在圆中，周长和直径之间具有什么关系呢？很多教师采用按部就班的教学方法，直接为学生呈现二者的关系，要求学生先记忆后理解，在这种教学模式中，学生缺乏主动思考，难以形成数学思维，更难以实现举一反三。要想弄清这一问题，教师首先要选择多个圆，将周长、直径展现出来，对数进行研究、对比，这样才能发现其中的规律。在教学中，教师可以为学生准备不同大小的圆的模型，带领学生测量圆的周长，用线绕圆一周，测量圆的周长，然后用直尺测量圆的直径，从“数”的角度分析圆的周长和直径之间的关系。

通过实际测量，学生可以发现，所测圆的周长和直径之间存在固定的关系，圆的周长是直径的三倍多，周长与直径的比值约为3.14。为进一步验证这一结论，教师可以引导学生绘制其他的圆，用灵活的方法测量圆的周长和直径，看圆的周长和直径的比值是否一直是不变的，用大量的测量和计算验证猜想。当学生完成对比和分析之后，教师就可以引入π的相关内容，让学生认识到，圆的周长和直径的比值为π。此外，教师可以继续提问：“圆的周长和直径的比值为π，当我们知道了圆的直径，可以直接求出周长吗？所用的公式是什么？”通过推理，学生可以得出C＝πd。在小学数学教学中，几何图形的教学是比较复杂的，教师需要引入数形结合的方法，以数解形，通过研究数的关系掌握形的关系，从而发现几何图形的内在规律。

（三）数形结合，解决实际问题

在小学数学教学中，学生解决实际问题的能力至关重要，数形结合思想的应用最终要落实到问题解决方面，这样才能达到学以致用的目的。数形结合思想是数学教学中的重要思想，该思想能够简化数学问题，提高学生思维的严谨性、灵活性，促进学生数学学科核心素养的提升。在教学中，教师需要引导学生运用数形结合思想解决问题，带领学生用“形”推导应用题中的未知条件，用算式表示解答问题的过程，简化问题的解决路径。

应用题1：甲车每小时行驶50 km，乙车每小时行驶75 km，甲车从A地出发，乙车从B地出发，两辆车同时出发，相向而行，相遇后4.5个小时甲车到达B地，那么A、B两地的距离是多少km？

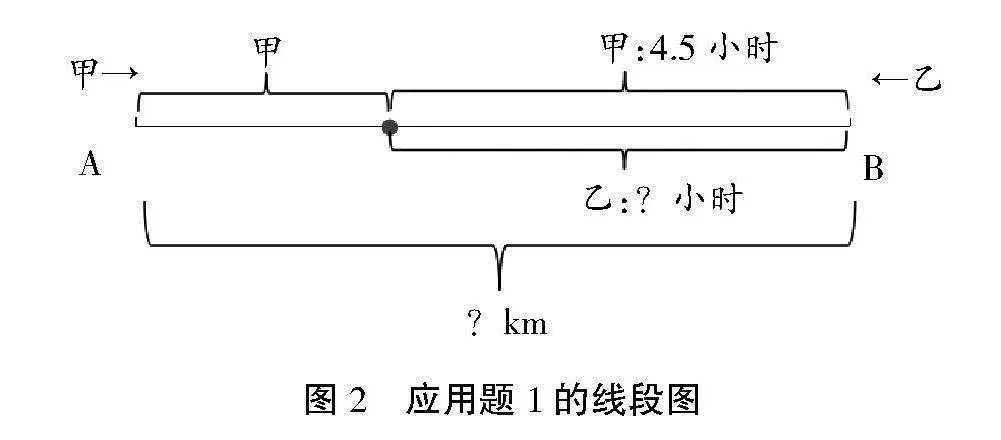
这道数学应用题是典型的行程问题，并且题目当中给出的条件比较复杂，已知两辆车的行驶速度，求两地的距离，解题的核心在于弄清相遇的时间。在解题中，很多学生难以抓住问题的关键点，无法将所有的已知条件整合到一起，在这种情况下，教师可以借助线段图（见图2）帮助学生分析题目中的条件，应用数形结合思想，让复杂的数学题更加直观。

在这道题中，教师可以结合线段图分析题意，圆点处是甲乙两车相遇的地方，相遇后，甲车又行驶了4.5个小时，才到达B地，此时教师可以提问：“甲车行驶4.5个小时的路程是多少？”学生可以结合题目中的已知条件，列出50×4.5＝225（km）。接下来，教师可以继续提问：“现在可以求出甲乙两车相遇的时间吗？图中甲行驶了4.5小时的路程，乙需要行驶多少小时？”根据题意及已得出的条件，学生可以很容易地列出算式：225÷75＝3（小时），进而求出两地距离为（50+75）×3＝375（km）。结合线段图，学生的思路能够更加清晰，最终找到问题的突破口，求出两车相遇所用的时间。

在解答类似的应用题时，很多应用题给出的条件存在迷惑性，学生一时之间难以理清思路，线段图能够帮助教师讲解应用题，辅助学生做题，简化学生的解题路径。

应用题2：儿子、爸爸和爷爷三人的年龄和是107岁，其中爷爷比爸爸大25岁，爸爸比儿子大23岁，三个人分别是多少岁？

该问题属于和差问题，这是小学数学教学中的常见问题，要求学生在给定条件下求解两个数的和或差。和差问题包含两类，分别是“和问题”和“差问题”，“和问题”是已知两个数的和，求解两个数，“差问题”是已知两个数的差求解两个数。在这道题中，已知条件中有三个人的年龄和，也有年龄差，学生需要灵活运用数学知识和技巧，分析条件，整理式子，最终得出答案。该题虽然不涉及复杂的计算，但很多学生抓不住问题的突破口，认为题目中的条件很难构建联系，解题效率较低。在数形结合思想的引导下，教师可以用线段图引导学生对问题中的条件进行分析，如图3所示。

线段图能够对应用题中的条件进行整理，从线段图中可以直观了解到爸爸和儿子的年龄差、爷爷和爸爸的年龄差，找到相等的部分和多出的部分，只要从107中减去（23+23+25），所得的差正好是儿子年龄的三倍。在解题时，学生首先可以求差，列式107-（23+23+25）＝36（岁），然后进行倍除，列式36÷3＝12（岁），得出儿子的年龄，最后再求出爸爸的年龄和爷爷的年龄，列式为12+23＝35（岁），35+25＝60（岁），所以儿子12岁，爸爸35岁，爷爷60岁。在和差问题中，数形结合思想能够将“和”“差”以直观的形态展示出来，帮助学生思考，让学生找到数量之间的关系，提高解题速度。

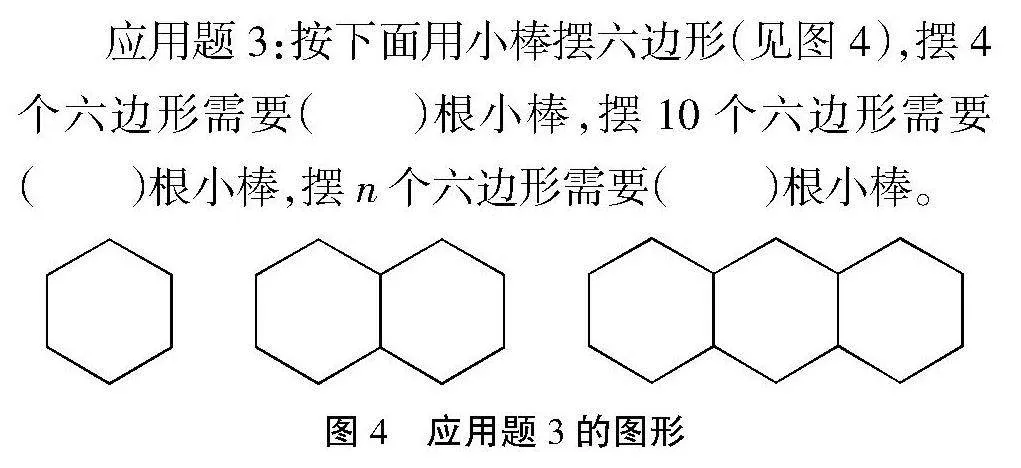
应用题3：按下面用小棒摆六边形（见图4），摆4个六边形需要（ ）根小棒，摆10个六边形需要

（ ）根小棒，摆n个六边形需要（ ）根小棒。

该题是一道找规律的问题，给出了图形，需要学生摸索其中的规律，并进行总结。在小学阶段，找规律的题大致可分为两类，一类是寻找“数”的规律，另一类是寻找“形”的规律，在寻找“形”的规律时，教师可以引导学生从数的角度进行思考，分析图形中边、角的个数，或者对周长、面积的规律进行探索，这些都是从数的角度寻找图形规律的方法。在解题时，教师需要构建“形”与“数”的连接，提问学生：“摆1个六边形需要几根小棒？摆2个六边形需要几根小棒？”通过图形，学生可以很轻松地回答出教师提出的问题，同时发现2个正六边形重合的部分，从不同角度摸索规律。

例如，有的学生把“摆1个六边形需要6根小棒，写成算式“5×1+1”，把“摆2个六边形需要11根小棒”写成“5×2+1”，把“摆3个六边形需要16根小棒”写成“5×3+1”，最终得出摆n个六边形需要5n+1根小棒。

还有些学生把“摆1个六边形需要6根小棒，写成算式“1×6-0”，把“摆2个六边形需要11根小棒”写成“2×6-1”，以此类推，得出摆n个六边形需要6n-（n-1）根小棒，即5n+1根小棒。在学生找规律的过程中，教师可以引导学生从图形上进行分析，找出列算式的规律，说出自己的思路。

在小学数学教学中，面对比较难的数学题，学生如果只分析题目中的文字，或者只观察题目中给出的图形，将很难抓住解题的重点。通过运用数形结合思想，学生可以画线段图，找出数量关系，还可以从数的角度对图形的规律进行思考，提高解题效率。因此，教师需要引导学生应用数形结合思想解答应用题，在教学中培养学生的数形结合思想，用图形理清思路，提高学生的解题速度。

综上所述，在小学数学教学中，教师需要认真思考数形结合思想对学生数学思维的促进作用，在课堂教学中充分运用数形结合思想，通过画图、呈现多媒体教学动画等方法，发挥数形结合思想的价值。数形结合思想是学习数学知识的基础思想，以形助数、以数解形、数形对比等都是数形结合思想的应用思路，教师需要遵循学生的认知规律，让数量关系和空间形式实现转化。在今后的小学数学教学中，教师需要不断创新教学方法，引入更多数学思想，优化教学手段，发展学生的数学思维，提升学生的解题能力。

（作者单位：甘肃省兰州市城关区雁北路小学）

编辑：赵文静

作者简介：祁淼（1986—），女，汉族，甘肃兰州人，本科，一级教师，研究方向：小学数学教育教学。