三维表面裂纹应力强度因子参数敏感性有限元分析

摘 要：三维表面裂纹是许多工程结构中普遍存在的一种缺陷，无论是在损伤容限设计或缺陷评估阶段，人们都要求对裂纹的应力强度因子进行精确的估计，这一参量对裂纹的预测和剩余疲劳寿命的估计起到至关重要的作用。借助有限元软件Abaqus和断裂力学软件Franc3d建立三维半椭圆表面裂纹实体模型，依据断裂力学相关知识，采用M-积分法，对含有表面裂纹的模型进行数值模拟，研究了模型在不同裂纹形状比（a / b = 1.5、1.36、1.25和1.15）以及裂纹倾角（θ = 0[°]、15[°]、30[°]和45[°]）下的裂纹扩展情况和应力强度因子参数敏感性。主要研究内容与结论如下：裂纹形状比a/b越大，应力强度因子越小，应力强度因子分布形貌由“凹”向“凸”转变；裂纹倾角达到0[°]时，裂纹深处应力强度因子最大，裂纹更容易扩展，随着裂纹倾角（0[°]、15[°]、30[°]和45[°]）的增大，应力强度因子逐渐减小。

关键词：三维表面裂纹；应力强度因子；参数敏感性；断裂力学；有限元分析

中图分类号：V215.6" "文献标识码：A" " 文章编号：1007 - 9734 （2024） 03 - 0018 - 08

0 引 言

表面裂纹是飞行器和压力容器中最为常见的裂纹形式之一，无论在损伤容限设计还是在缺陷评定阶段，人们都需要尽可能准确地估算构件中裂纹的应力强度因子（SIF），因为这一参量是预测含裂纹构件的断裂以及估算剩余疲劳寿命的主要依据[1]。从严格的角度来说，大多数的裂纹问题均为三维问题，对于含有裂纹缺陷的复杂构件来说，三维裂纹问题的探究更具实际工程价值。随着断裂力学的发展，三维裂纹问题得到了广泛的研究，但由于其计算参数众多、计算过程烦琐，使得其理论研究与二维裂纹相比仍有很大差距。对于三维裂纹问题，多数学者采用数值方法和近似方法进行分析。

在数值法方面，李英治[2]利用“局域-全局解析法”获得了三维有裂纹体的应力-应变场，构建了一个三维有裂纹体的奇异性单元，对其进行了应力强度因子的计算，并研究了不同尺寸的薄板的应力强度因子。谢伟[3]针对传统裂纹闭合方法的局限，提出了一种改进的裂纹闭合方法，该方法突破了裂纹面必须具有相同的面积和几何对称性的约束，得到了更高的精度。王永伟[4]在利用有限元法计算应力强度因子时，在裂缝前沿采用了三维等参退化奇性单元，分析了网格密度对计算结果的影响，并提出了一种无因子化的形状因子，用来表达应力强度因子法可应用于含裂纹的三维构件的应力强度因子的计算。孙光耀[5]利用Abaqus及Franc3d结合的方法，对变速箱齿轮边缘的三维单裂纹在不同位置上的扩展变化规律进行了分析。随着裂纹扩展阶段的增加，三种类型的裂纹KI值都有所增加，并且在齿根部当量弯曲应力达到最大时，其应力强度因子始终处于最大值，说明试验结果是可信的。Shivakumar[6]提出了一种对网格尺寸不敏感的虚拟裂纹闭合法，它可以避免使用奇异元。通过在有限元软件Abaqus中自定义疲劳单元，进而可靠地计算三维裂纹体中的应力强度因子，并对裂纹扩展过程进行模拟，从而进行疲劳寿命预测。

对于近似解法的研究，赵伟 [7]在已有的二维加权函数理论的基础上，结合片条综合方法，提出了一种新的、高精度的、高效的求解裂纹前缘应力强度因子及裂纹表面位移的方法——三维裂纹加权函数法，并在此基础上建立相应的权函数，从而避开了三维位移场的构建。Rice[8]提出了一种线性弹簧模型，用于分析在拉伸和弯曲载荷下的平板中的表面裂纹问题。Fujimoto[9]提出的片条合成方法，该方法不需要构建三维位移场，也不需要求得平均应力强度因子，具有较高的适用性。但是，由于没有给出片条的完全表征，且没有考虑片条方向对片条弹性模量的影响，导致计算结果存在较大误差。因此，尽管基于近似求解的理论提出了许多可用于三维裂纹应力强度因子计算的解析模型与方法，但是，这些理论与方法都存在一定的限制，且仅适用于少数几个几何或载荷工况，难以获得裂纹前沿的应力强度因子[10-12]。

以上对三维表面裂纹的研究和应用现状进行了总结和评估。总体而言，目前国内外学者对应力强度因子的研究多停留在理论推导与试验阶段，而对应力强度因子的敏感性研究较少，相关学术研究尚未达成普遍适用的分析评估方法，且基础研究成果尚不足以满足工程需求。因此，深入展开三维表面裂纹应力强度因子相关领域的基础和应用研究不仅具有重要的学术价值，也是现实的迫切需要。本文中借助有限元软件Abaqus和断裂力学软件Franc3d，建立了三维半椭圆表面裂纹实体模型，并依据断裂力学相关知识，对含有表面裂纹的模型进行数值模拟，采用M-积分法研究了模型在不同裂纹形状比（a / b = 1.5、1.36、1.25和1.15）以及不同裂纹倾角（θ = 0°、15°、30°和45°）下的裂纹扩展情况和应力强度因子参数敏感性，为后期裂纹扩展轨迹预测和寿命分析提供理论依据。

1 三维表面裂纹应力强度因子数值分析方法

1.1 三维表面裂纹尖端奇异元

在断裂力学中，应力强度因子（SIF）是一个用于描述裂纹尖端应力场强度的物理量，它是与裂纹几何尺寸、载荷大小和材料弹性特性等相关的函数。应力强度因子反映了裂纹顶端附近的应力场强度，并用于定量评价裂纹扩展的趋势或推动力。在进行应力强度因子K的求解时，往往缺少手册数据或解析解数据，需要依靠数值解法来计算应力强度因子，这就要求根据当前的结构构形、裂纹构形及尺寸建立和求解有限元模型并计算应力强度因子。

在弹性力学中，可以用一个方程来表达裂尖附近的应力场：

[σ=KI2πrfθ] （1）

式中：[r]、[θ]为计算所处位置的椭圆极坐标；[fθ]为无量纲系数。

当[r]→0，[θ]→0时，在裂尖附近的压力会趋向于无限大，这就是所谓的应力奇异。但事实上，这是不可能的，一旦压力超过了材料的承受范围，裂纹就会产生一种特殊的塑性区，这种塑性区就会被释放出来。然而，尽管在这种情况下，裂尖上的应力趋向于无限，但它的应力强度因子仍是一个有限的数值。为了达到满意的精度，裂纹尖端的网格需要进行十分精细的划分，为了避免这个缺点，发展了多种具有[r-12]奇异性的奇异元。采用裂尖奇异元模拟裂纹模型，可以很好地模拟裂尖应力应变场的奇异性，其单元形式及网格形式如图1所示。

本文中裂纹前缘网格划分时所采用的单元类型均为三维裂纹尖端奇异元。

1.2 三维表面裂纹应力强度因子计算方法

在计算裂纹尖端应力场时，应力强度因子的求解是一个重要的步骤。通常情况下，应力强度因子可以被写成以下的公式：

[K=fσπα] （2）

式中：[σ]为名义应力，即裂纹位置上按无裂纹计算的应力；[a]为裂纹几何尺寸；[f]为形状系数（与裂纹几何尺寸、位置等有关），反映了构件和裂纹尺寸对裂纹尖端应力场的影响。

基于软件Franc3d进行裂纹应力强度因子计算时，常用的计算方法有两种：它们分别是M-积分法和位移相关法。位移相关法是一种比较容易理解和实施的解析法，但精度较差。而M-积分是Franc3d系统默认的方法，在数值上与[J]积分非常相似，并且具有极高的求解精度。M-积分也称为交互积分，它可以考虑多种因素的影响，如温度、裂纹面的接触、裂纹面的牵引和残余应力等，而且还能实现多种情况下的应力强度因子叠加计算。因此，在Franc3d中，通常使用M-积分计算应力强度因子，以获得更为准确的计算结果。这里选用M-积分求解裂纹。其表达式为：

[M（1，2）=Γσ（1）ij∂u（2）i∂x1+σ（2）ij∂u（1）i∂x1∂q∂xj ds-ΓW1，2δ1j∂q∂xj ds-ΓW1，2δ1j∂q∂xjds ] （3）

式中：[Γ]为围绕裂纹尖端的积分回路。

[W（1，2）=σ（1）ijε（2）ij=σ（2）ijε（1）ij] （4）

M-积分与应力强度因子关系为：

[M（1，2）=1-v2EKI（1）KI（2）+1-v2EKII （1）KII （2）+1+vEKIII （1）KIII （2）+1+νEKΙΙΙ（1）KΙΙΙ（2）] （5）

式中：KI、KII和KIII为三种基本裂纹形式对应的应力强度因子。大量的模拟实验研究表明，在实际工程中，疲劳裂纹扩展主要以张开型裂纹为主，因此本文主要以I型裂纹为研究对象，探讨I型应力强度因子的变化规律。

1.3 三维表面裂纹应力强度因子敏感性分析

本文首先使用三维Cad软件Solidworks建立实体模型，然后导入有限元网格划分软件Hypermesh对其网格进行划分并确定裂纹扩展区域。最后，通过有限元软件Abaqus和Franc3d进行三维表面裂纹应力强度因子敏感性分析，研究裂纹形状比以及裂纹倾角等因素的改变对应力强度因子的变影响规律。本文的研究对象为三维半椭圆表面裂纹有限元模型，根据以上数值模拟的思想，结合断裂力学相关知识，数值模拟流程如图2所示。

2 三维半椭圆表面裂纹的有限元模型

2.1 模型几何参数

本节分析含表面裂纹的三维结构，受远端拉伸载荷作用的裂纹扩展问题。模型尺寸为长100 mm，宽100 mm，厚度100 mm，半椭圆表面裂纹深度为长半轴a = 15 mm，短半轴b = 10 mm，圆心位于对称面长边中点处，受轴向载荷[σ=100 MPa]。模型材料参数为：弹性模量E = 210 GPa，泊松比[ν ]= 0.3。材料选取Q235结构钢，结构如图3所示。

2.2 有限元模型建立

基于三维Cad软件Solidworks建立正方体实体模型，如图4所示。

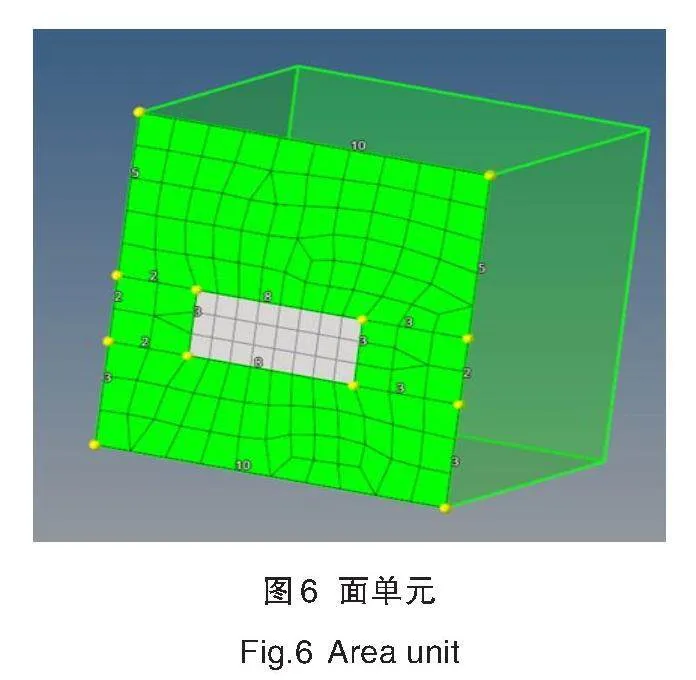
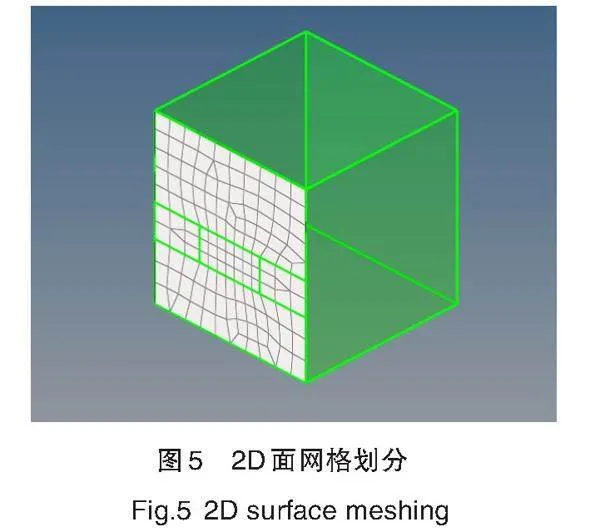
将实体模型导入Hypermesh软件中，进入Geom主菜单点击“Solid Edit”进行实体分割。分割好后，整个面就分为了两部分，可以分别对其进行网格划分。首先，需要用四节点2D单元控制六面体单元形状，进行裂纹扩展区域划分，结果如图5所示。同样，对其他区域进行网格划分，分割后裂纹扩展区域和其他区域网格不同，方便进行子模型构建。该面显示黄绿色，即为映射状态，如图6所示。

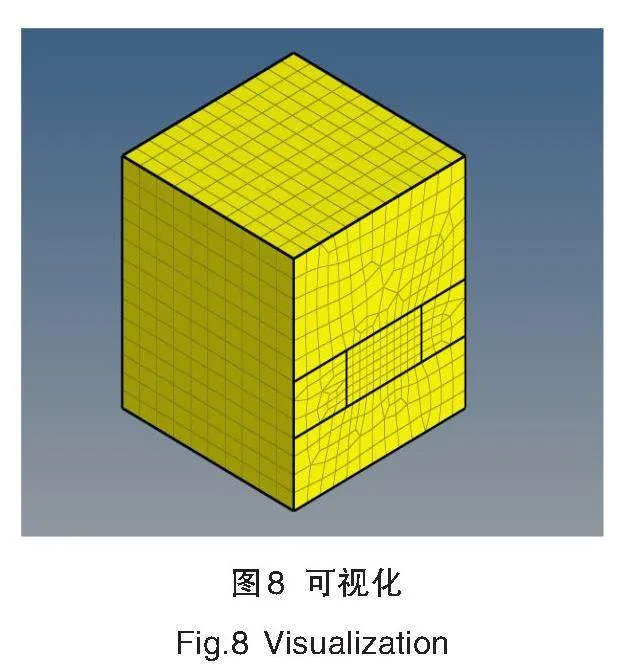
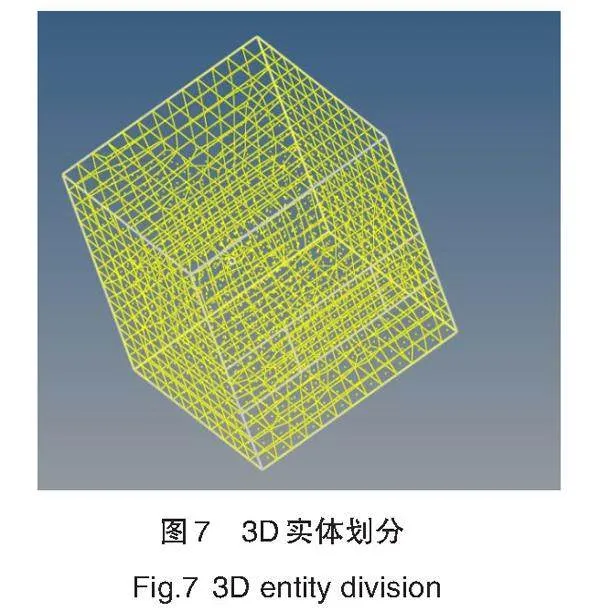
接着，进入3D主菜单点击Solid Map，进行六面体实体网格划分。通过面划分实体，点击目标面，划分方向沿四条边并进行网格单元长度设置，设置完成后，即可完成实体块网格划分，如图7、图8所示。

为方便在Franc3d软件中快速准确地添加表面裂纹，需要将裂纹扩展区域从整体模型中切割出来。在分析步骤中，创建Set单元集。按照逐个单元进行分割，将中间整齐的六面体单元区域确定为裂纹添加区域，如图9、图10所示。采用C3D8R型八结点线性六面体单元，对整个模型进行精细划分，最小网格数为1 mm。

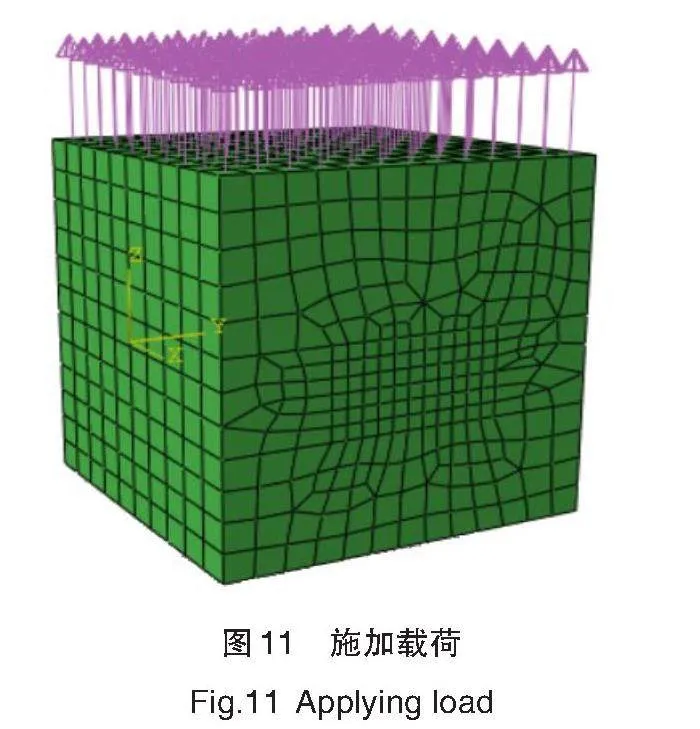
将经过Hypermesh网格划分后的有限元模型导入Abaqus中，对其设定其材料参数并施加载荷，见图11。

2.3 三维表面裂纹前缘应力强度因子计算

通过Franc3d软件读取子模型、使用图形化的初始裂纹引入向导，对子模型重新划分，然后将含有裂纹的子模型和剩余部分的模型重新整合。最后采用自适应网格划分方法对子模型网格进行更新，见图12。

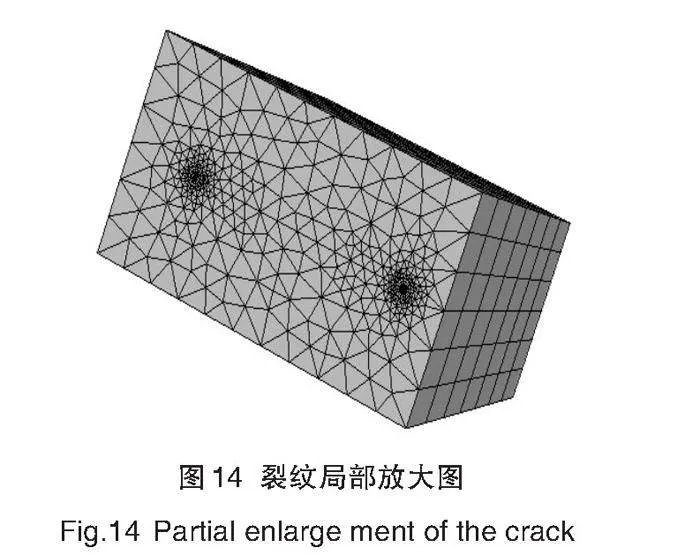
为了体现裂纹尖端应力的奇异性，将非裂纹两侧边缘的端点用来描述裂尖应力的奇异性；在裂纹前缘定义16个圆周圆环，以便更精细地划分裂纹前缘。自适应网格划分方法会在裂纹区域自动引入细化网格并过渡到远离裂纹的较大单元。仅对裂纹区域的网格加密，保证了模型的完整性，也能更加精确地反映出裂纹特性。引入裂纹后正方体模型的网格及其裂纹局部放大，如图13、图14所示。

求解时，Franc3d可以自动调用Abaqus外部求解器，自动读取应力分析结果计算所有裂纹前缘节点的应力强度因子。

3 三维表面裂纹应力强度因子敏感性分析

根据上述步骤完成三维半椭圆表面裂纹有限元建模后，利用断裂分析软件Franc3d计算出拉伸载荷F = 100 N下的裂纹尖端应力强度因子，研究裂纹扩展情况；此外，在保持其他约束条件不变的基础上，研究不同裂纹形状比a / b和裂纹倾角下的应力强度因子敏感性。

3.1 三维表面裂纹应力强度因子计算

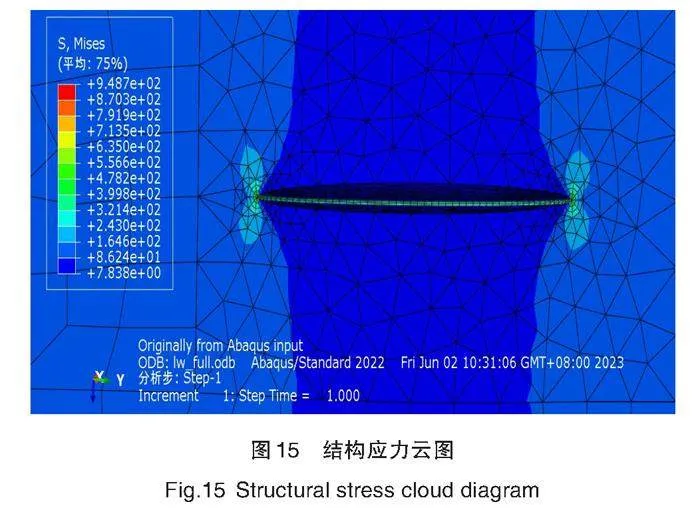
使用M-积分法计算出初始裂纹前缘上的应力强度因子KI， KII和KIII的值。在施加载荷100 N的情况下，将Franc3d结果文件导入Abaqus软件进行计算分析，结构应力云图如图15所示。

由上图可以看出，裂纹面相对位移垂直于裂纹平面，被拉开一定角度。裂纹前缘存在应力集中现象，应力最大处在裂纹尖端，应力从裂纹尖端沿半椭圆弧线往两边减小后增大。

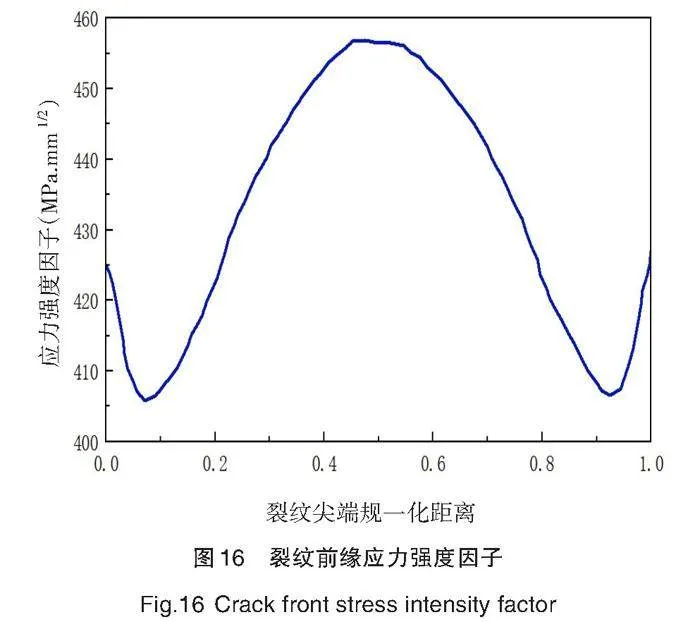
在裂纹进行应力强度因子分布曲线分析时，对裂纹前缘进行归一化处理，其中横坐标的“0”表示裂纹左端边缘的表面点，“1”表示裂纹右端的表面点，“0.5”代表裂纹的最深处位置。

KI结果如图16所示，整体形状呈现“波浪”型，裂纹尖端应力强度因子沿着裂纹最深处的方向呈90度对称分布。由于表面点没有材料约束，接近平面应力状态，裂纹尖端存在材料约束，无限接近于平面应变状态，应力强度因子会先减小后增大，增长速度由快到慢。裂纹最深处的应力强度因子最大，KImax为450.8742 MPa·mm1/2，左端点的应力强度因子为420.2543 MPa·mm1/2，右端点的应力强度因子为420.1729 MPa·mm1/2，半椭圆左端点和右端点的应力强度因子基本相等。

3.2 裂纹形状比对应力强度因子的影响

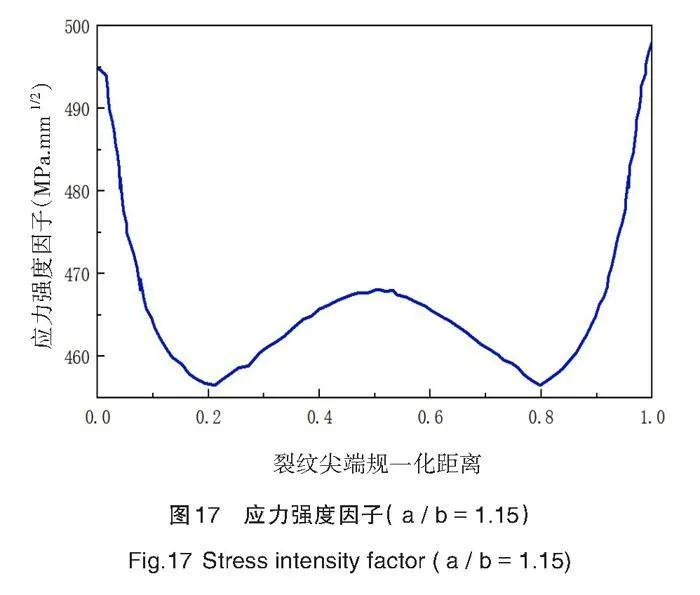
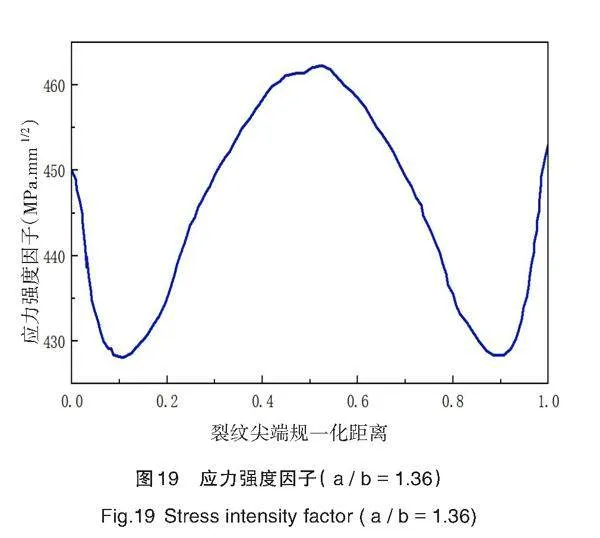
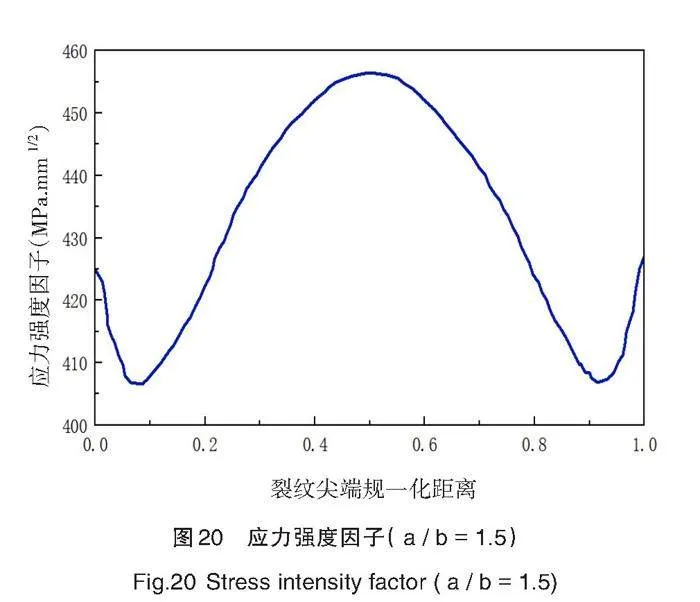
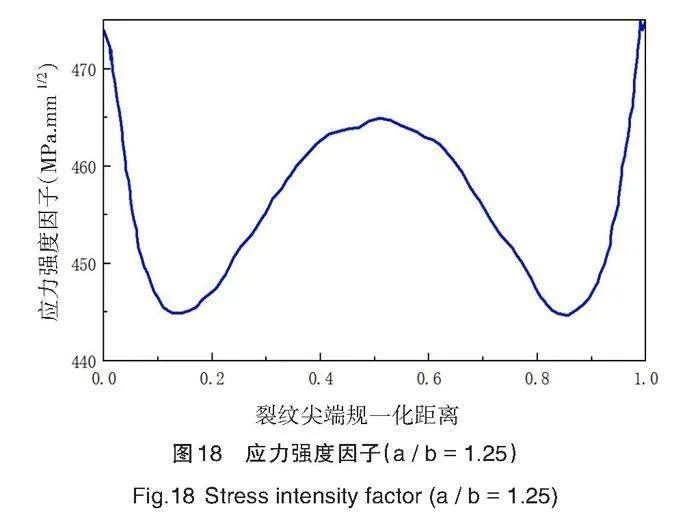
在其他约束条件不变的情况下，改变裂纹形状比a / b，对应力强度因子再次进行研究。保持在实体模型上下表面施加的拉伸载荷100 N不变，改变裂纹短半轴b，分别取11 mm、12 mm和13 mm，保持长半轴a =15 mm，观察不同形状比对应力强度因子的影响。对结果进行统计讨论，得出裂纹形状比改变对应力强度因子的影响规律，不同情况裂纹形状比的应力强度因子结果示意图如图17～图20所示。

通过计算结果分析可知，同一裂纹长度2a = 30 mm，随着裂纹形状比的增加，应力强度因子减小。裂纹逐渐扩张，裂纹口增大，裂纹前缘出现应力集中现象。当裂纹形状比（ a / b ）较小时，裂纹最深处的K值小于裂纹尖端表面，导致裂纹在深度方向上的扩展较慢；随着形状比的增大，裂纹最深处的K值逐渐大于裂纹表面尖端，裂纹沿深度方向扩展的速率逐渐大于沿表面方向扩展的速率。

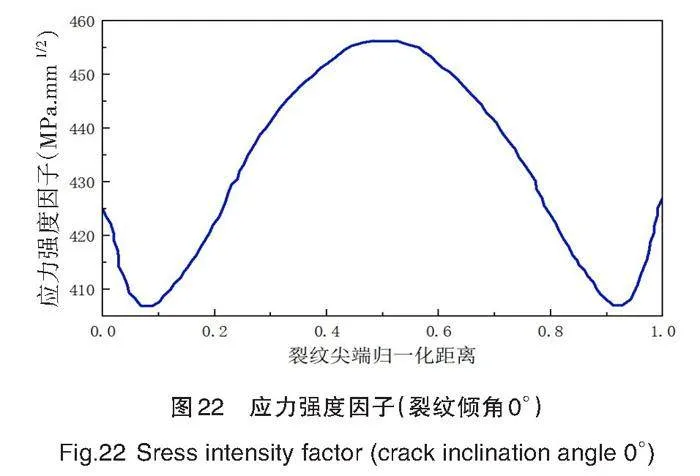
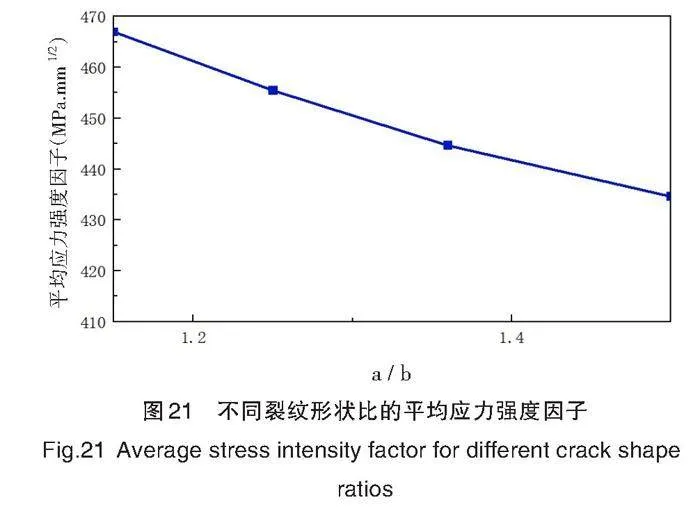
由平均应力强度因子曲线图21可知，随着裂纹形状比的增大，应力强度因子减小，裂纹整体发生扩展的趋势不断增大。

综上所述，裂纹前缘的应力强度因子在裂纹扩展过程中受形状比的作用，且应力强度因子分布形貌由“凹”向“凸”转变。

3.3 裂纹倾角对应力强度因子的影响

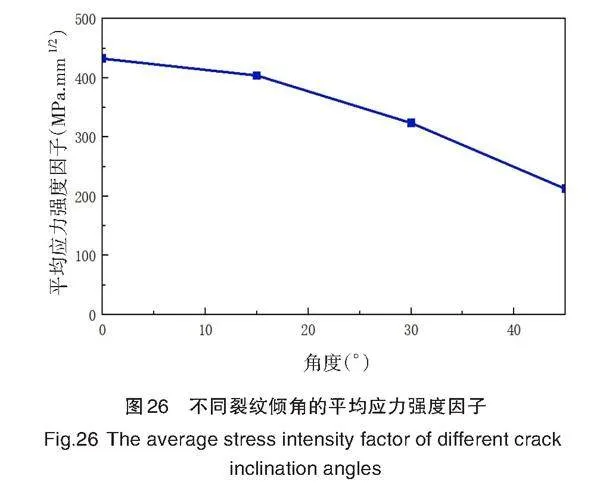
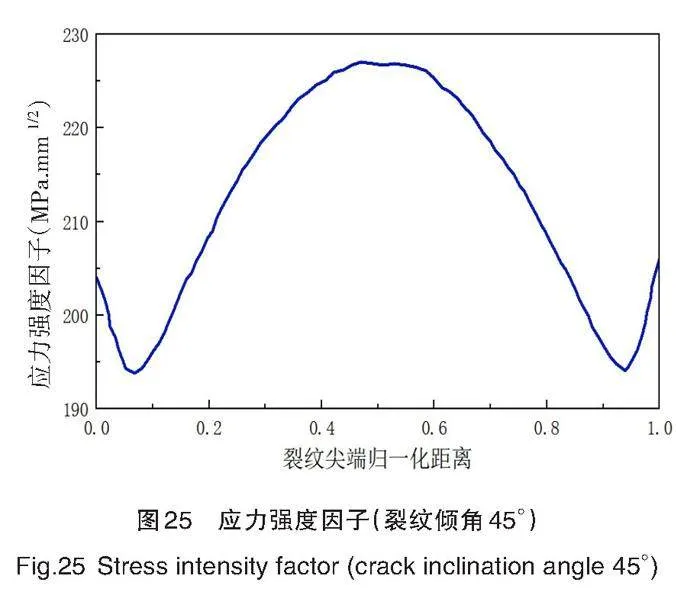
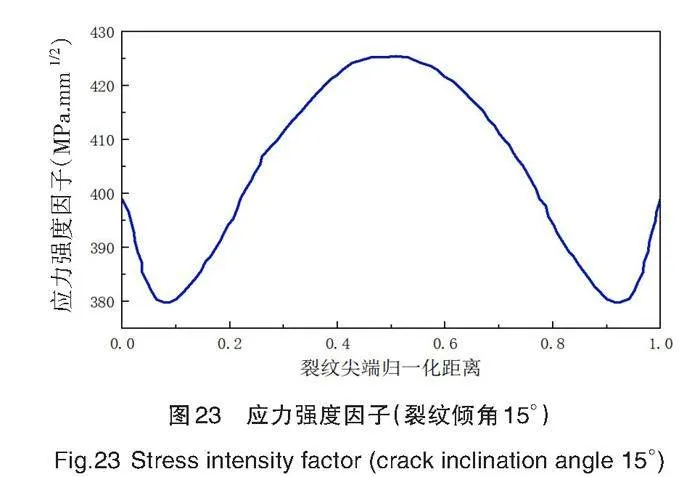
根据正应力[σ=FA]可知，如果在保持拉伸载荷不变的情况下，改变裂纹倾角，半椭圆裂纹的有效接触面积会减小，这也间接改变了裂纹的几何形状，应力强度因子也会发生变化。因此，在保持其他约束条件的情况下，改变裂纹的倾斜角（0°、15°、30[°]和45[°]），研究裂纹倾角变化对裂纹扩展和应力强度因子的影响。不同情况裂纹倾角的应力强度因子结果示意图如图22～图25所示。

由应力强度因子曲线图22～图25可知，即便改变裂纹倾角，裂纹形状依旧呈现波浪状。裂纹最深处应力强度因子大于非裂纹尖端前缘上的两个应力强度因子。

由平均应力强度因子曲线图26可知，随着裂纹倾角（0°、15°、30°和45[°]）的增大，应力强度因子减小。裂纹位置从水平逐渐倾斜于竖直，应力强度因子逐渐减小，裂纹不容易扩展，这是因为拉伸载荷作用的有效裂纹平面面积越来越小。

4 结 论

本文使用有限元软件Abaqus和Franc3d研究了三维半椭圆表面裂纹的应力强度因子，分析了不同裂纹形状比和倾角下的裂纹扩展和应力强度因子的变化规律，能够实现任意形状三维实体模型的划分，且结果可信度较高。本文中主要内容与结论如下：

（1）裂纹前缘的应力强度因子在裂纹扩展过程中受形状比的作用，当裂纹形状比增大时，应力强度因子减小，且应力强度因子分布形貌由“凹”向“凸”转变。

（2）在裂纹的不同位置，裂纹倾角对I型裂纹应力强度因子的影响趋势相同。随着裂纹倾角的增大，裂纹越来越不容易扩展，应力强度因子减小。当裂纹倾角达到0°时，裂纹尖端应力强度因子最大，说明此时的裂纹最容易扩展，裂纹倾角从0°达到45°时，应力强度因子迅速减小，说明与水平面产生的倾角越大，裂纹就相对更安全，不容易发生扩展。

参考文献：

［1］吴连生，于培师，韦朋余，等.基于三维理论的TC4ELI钛合金疲劳裂纹扩展研究[J].船舶力学，2022（9）：1354-1362.

［2］李英治，李敏华，柳春图，等.含表面裂纹三维体裂纹尖端应力应变场及应力强度因子计算[J].中国科学：数学， 1988（8）：46-60.

［3］谢伟，黄其青.改进的三维虚拟裂纹闭合方法[J].西北工业报，2008，26（1）：116-120.

［4］王永伟，林哲.表面裂纹的三维模拟及应力强度因子计算[J].中国海洋平台，2006（3）：23-26.

［5］孙光耀.风电机组齿轮裂纹应力强度因子及疲劳寿命分析[D].乌鲁木齐：新疆大学，2021.

［6］SHIVAKUMAR K N，TAN P W，NEWMAN J C.A virtual crack-closure technique for calculating stress intensity factors for cracked three dimensional bodies[J].International Journal of Fatigue， 1988， 36（3）： 43-50.

［7］赵伟，颜鸣皋，吴学仁. 三维裂纹分析的权函数理论及应用[D].北京：北京航空材料研究所，1988.

［8］RICE J R，LEVY N.The part-through surface crack in an elastic plate[J].Journal of Applied Mechanics，1972（1）： 185-194.

［9］FUJIMOTO W T.Determination of crack growth and fracture toughness parameters for surface flaws emanating from fastener holes[C]. Valley Forge： Proc. of the AIAA/ASME/SAE 17th SDM Meeting， 1976.

［10］曾苇鹏，鲁嵩嵩，刘斌超，等.飞机薄壁结构面外载荷下三维疲劳裂纹扩展仿真分析[J] .航空工程进展，2022，13（3） ：23-31.

［11］黄益昌，张继旺，苏凯新，等.高速列车铸钢制动盘表面应 力强度因子分析[J/OL].机械科学与技术，2023-06-02. https：//doi.org/10.13433/j.cnki.1003-8728.20230262

［12］赵慧，吕毅，窦鹏鹏.三维裂纹扩展轨迹的厚度效应研究[J].兵器装备工程学报，2019，40（8）：219-225.

责任编校：田 旭，刘 燕

Finite Element Analysis of Parameter Sensitivity of Three-Dimensional Surface Crack Stress Intensity Factors

ZHAO Hui1， ZHAO Wei2， SONG Lei3， LIU Wei1

（1. School of Aircraft Engineering， Xi’an Aeronautical Institute， Xi’an 710077， China;

2. Taiyuan International Airport Co.， Ltd， Communication Navigation Department， Taiyuan 030031， China;

3. Steel-making Plant 2， Shanxi Taigang Stainless Steel Company， Taiyuan 030003， China）

Abstract：Three-dimensional surface cracks are a common defect in many engineering structures.Whether in damage tolerance design or defect assessment stages，accurate estimation of stress intensity factors for cracks is required. This parameter plays a crucial role in predicting cracks and estimating the remaining fatigue life. Utilizing the finite element software Abaqus and the fracture mechanics software Franc3d，a three-dimensional semi-elliptical surface crack solid model was established. Based on fracture mechanics knowledge and using the M-integral method， numerical simulations were performed on models with surface cracks. The study investigated crack propagation and sensitivity of stress intensity factor parameters under different crack shape ratios （a / b = 1.5，1.36，1.25，and 1.15） and crack inclinations （θ = 0°，15°，30°，and 45°）.The main research content and conclusions are as follows： The larger the crack shape ratio a/b，the smaller the stress intensity factor， and the distribution morphology of the stress intensity factor changes from\"concave\"to\"convex\".When the crack inclination reaches 0°，the stress intensity factor is maximal at the crack's depth， making the crack more prone to propagation. As the crack inclination （0°，15°，30°，and 45°） increases， the stress intensity factor gradually decreases.

Key words： three-dimensional surface crack; stress intensity factor; parameter sensitivity; fracture mechanics; finite element analysis

收稿日期：2024-01-08

作者简介：赵 慧，男，山西忻州人，讲师，研究方向为飞机结构强度。