Jafari-Sprott混沌系统滑模同步两个方案

摘 要：文章研究了Jafari-Sprott混沌系统的滑模同步问题，以李雅普诺夫稳定性理论和同步控制相关理论为基础，得出了同步控制的研究结论，并给出实现Jafari-Sprott混沌系统同步的两种方案。最后用MATLAB做出数值仿真，画出了吸引子相图和系统的误差曲线，对所得结果进行了数值验证，确定了同步方案的可行性与有效性.

关键词：混沌系统；滑模；同步

中图分类号： TV213.4" 文献标识码： A" 文章编号：1007 - 9734 （2024） 03 - 0104 - 04

0 引 言

混沌系统包含复杂的动力学行为，从而引起了控制界众多学者的高度关注［1-5］，关于混沌理论及其应用的研究已成为非线性科学研究中最重要的前沿课题之一。混沌同步属于混沌控制的范畴，目前，有关混沌系统同步控制的研究已取得了丰富的研究成果［6-10］。滑动模态控制方法的引入，使得复杂的非线性混沌同步控制问题变得迎刃而解。例如：文献［11］利用比例积分滑模研究了分数阶大气混沌系统的同步；文献［12-14］研究了分数阶混沌系统的自适应滑模同步；文献［15］研究了Victor-Carmen分数阶混沌系统自适应比例积分滑模同步；文献［16］基于新型滑模同步方法研究了Victor-Carmen分数阶混沌系统的同步问题；文献［17］研究了不确定R[o]ssler分数阶混沌系统的自适应滑模同步；文献［18］基于三个控制方案研究了金融分数阶混沌系统滑模同步。另一方面Jafari-Sprott混沌系统因其十分丰富的密匙参数与系统信息受到高度关注，文献［19］研究了Jafari-Sprott整数阶混沌系统的信息熵、李亚普诺夫指数谱、吸引子与分岔等动力学行为；本文根据稳定性理论和同步控制方法研究Jafari-Sprott混沌系统的滑模同步，得出了实现Jafari-Sprott混沌系统同步的两种方案。

1 数学模型与主要结果

1994年，美国学者Sprott J C通过计算机穷举法发现了19个混沌系统［19］，这19个系统被称为Sprott系统，编号为Sprott A到Sprott S。这些系统可以写出或是包含一个二次非线性项的六项式，或是包含两个二次非线性项的五项式，这19个系统不能通过变量替换而相互转换。Sprott系统方程简单，便于电路实现，在混沌扩频通信和混沌保密通信中有着很好的应用前景。Jafari S 和Sprott J C在2013年提出了Jafari-Sprott混沌系统［20］，对整数阶Jafari-Sprott系统方程做出动力学分析，方程如下：

[x=yy=-x+yzz=-x-axy-bxz] （1）

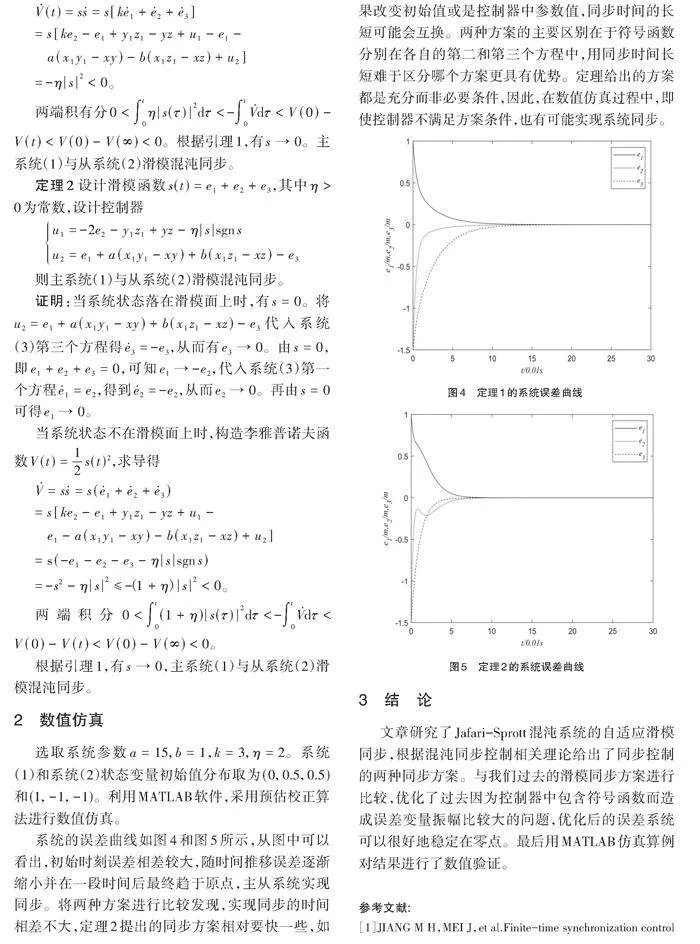
选取系统参数[a=15，b=1] ，系统（1）呈现出混沌态，其吸引子相图如图1所示。初始值设置为[（x（0），y（0），z（0））=（0，0.5，0.5）]。

以系统（1）作为主系统，设计从系统如下：

[x1=y1y1=-x1+y1z1+u1z1=-x1-ax1y1-bx1z1+u2] （2）

定义误差变量[e1=x1-x，e2=y1-y，e3=z1-z，]系统（2）与系统（1）中对应方程相减得误差系统：

[e1=e2e2=-e1+y1z1-yz+u1e3=-e1-ax1y1-xy-bx1z1-xz+u2] （3）

李雅普诺夫指数[λ1=0.7394，λ2=-0.9070，λ3=-0.2922]，李雅普诺夫指数图谱如图2所示，分岔图如图3所示。

引理1[21]若函数[f（t）]在[[0，+∞）]上一致连续，并且[0+∞f（t）dt]存在，则有[limt→∞f（t）=0]。

定理1 设计滑模函数[s（t）=ke1+e2+e3]，其中[kgt;2]为常数，

[u1=-ke2-y1z1+yzu2=2e1+ax1y1-xy+bx1z1-xz-ηssgns]

则主系统（1）与从系统（2）是滑模混沌同步的。

证明：当系统状态落在滑模面上时，[s=0]。根据系统（3）第一个方程有

[e1=e2] （4）

将[u1=-ke2-y1z1+yz]代入系统（3）第二个方程有

[e2=-e1-ke2] （5）

由式（4）和式（5）得[e2=-e1-ke2=-e2-ke2]，求解[e2]作为未知函数的微分方程，对应的特征方程为[λ2+kλ+1=0]，特征值为[λ=-k±k2-42]；由[kgt;2]，[λ]具有负实部，可知[e2→0]；结合式（5）得到[e1→0]；再由[s=0]，即[ke1+e2+e3=0]，可得到[e3→0]。

当系统状态不在滑模面上时，构造李雅普诺夫函数[V（t）=12s（t）2]，求导得

[V（t）=ss=ske1+e2+e3]

[=s[ke2-e1+y1z1-yz+u1-e1-ax1y1-xy-bx1z1-xz+u2]=-ηs2lt;0。]

两端积有分[0lt;0tηs（τ）2dτlt;-0tVdτlt;V0-Vtlt;V0-V∞lt;0]。根据引理1，有[s→0]。主系统（1）与从系统（2）滑模混沌同步。

定理2 设计滑模函数[s（t）=e1+e2+e3]，其中[ηgt;0]为常数，设计控制器

[u1=-2e2-y1z1+yz-ηssgnsu2=e1+ax1y1-xy+bx1z1-xz-e3]

则主系统（1）与从系统（2）滑模混沌同步。

证明：当系统状态落在滑模面上时，有[s=0]。将[u2=e1+ax1y1-xy+bx1z1-xz-e3]代入系统（3）第三个方程得[e3=-e3]，从而有[e3→0]。由[s=0]，即[e1+e2+e3=0]，可知[e1→-e2]，代入系统（3）第一个方程[e1=e2]，得到[e2=-e2]，从而[e2→0]。再由[s=0]可得[e1→0]。

当系统状态不在滑模面上时，构造李雅普诺夫函数[V（t）=12s（t）2]，求导得

[V=ss=se1+e2+e3]

[=s[ke2-e1+y1z1-yz+u1-e1-ax1y1-xy-bx1z1-xz+u2]=s-e1-e2-e3-ηssgns=-s2-ηs2≤-（1+η）s2lt;0。]

两端积分[0lt;0t1+ηs（τ）2dτlt;-0tVdτlt;V0-Vtlt;V0-V∞lt;0]。

根据引理1，有[s→0]，主系统（1）与从系统（2）滑模混沌同步。

2 数值仿真

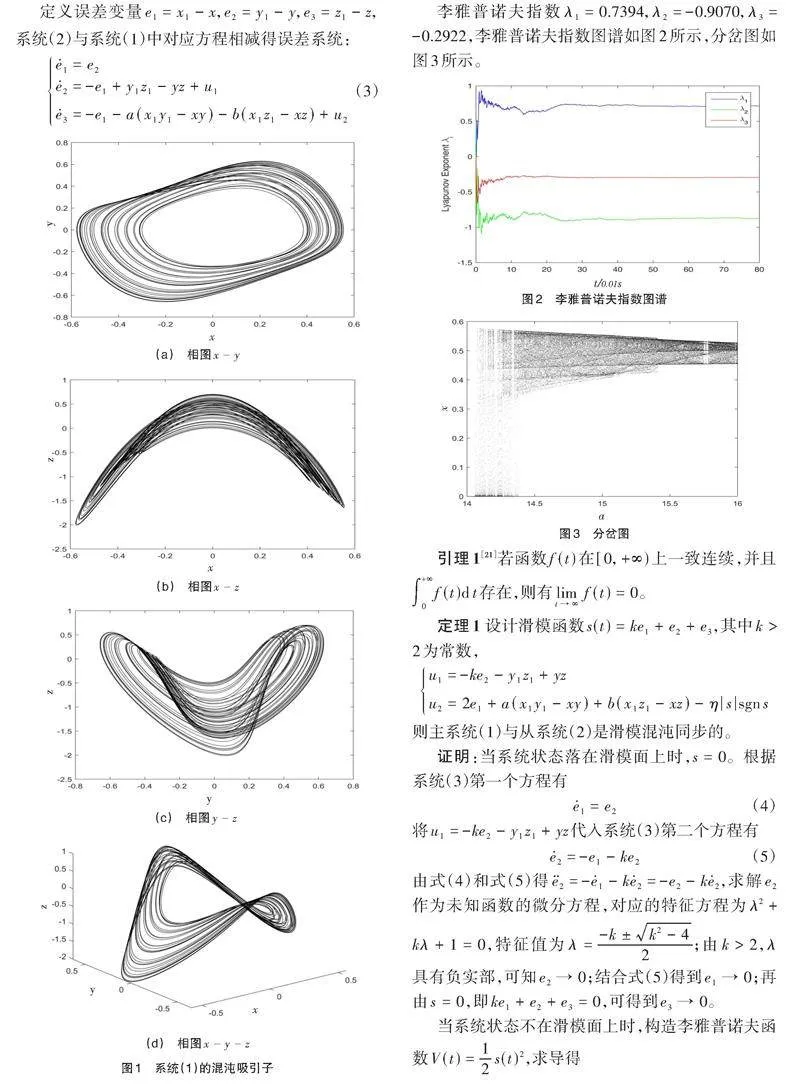
选取系统参数[a=15，b=1]，[k=3，η=2]。系统（1）和系统（2）状态变量初始值分布取为[（0，0.5，0.5）]和[（1，-1，-1）]。利用MATLAB软件，采用预估校正算法进行数值仿真。

系统的误差曲线如图4和图5所示，从图中可以看出，初始时刻误差相差较大，随时间推移误差逐渐缩小并在一段时间后最终趋于原点，主从系统实现同步。将两种方案进行比较发现，实现同步的时间相差不大，定理2提出的同步方案相对要快一些，如果改变初始值或是控制器中参数值，同步时间的长短可能会互换。两种方案的主要区别在于符号函数分别在各自的第二和第三个方程中，用同步时间长短难于区分哪个方案更具有优势。定理给出的方案都是充分而非必要条件，因此，在数值仿真过程中，即使控制器不满足方案条件，也有可能实现系统同步。

3 结 论

文章研究了Jafari-Sprott混沌系统的自适应滑模同步，根据混沌同步控制相关理论给出了同步控制的两种同步方案。与我们过去的滑模同步方案进行比较，优化了过去因为控制器中包含符号函数而造成误差变量振幅比较大的问题，优化后的误差系统可以很好地稳定在零点。最后用MATLAB仿真算例对结果进行了数值验证。

参考文献：

［1］JIANG M H，MEI J，et al.Finite-time synchronization control of a class of memristor-based recurrent neural networks[J].Neural Networks： The Official Journal of the International Neural Network Society，2015，63：133-140.

［2］SONG S，ZHANG B Y，SONG X N.et al.Fractional-order adaptive neuro-fuzzy sliding mode H∞ control for fuzzy singularly perturbed systems[J].Journal of the Franklin Institute，2019，356（10）：5027-5048.

［3］SONG S，ZHANG B Y，SONG X N，et al.Neuro-fuzzy-based adaptive dynamic surface control for fractional-order nonlinear strict-feedback systems with input constraint[J].IEEE Transactions on Systems，Man and Cybernetics：Systems， 2019，29（9）：3347-3359.

［4］HAN X M，WU H Q.Adaptive exponential synchronization of memristive neural networks with mixed time-varying delays[J].Neurocomputing，2016，20（3）：40-50.

［5］TCHINDA S， MPAME G，TAKOUGANG A，et al.Dynamic analysis of a snap oscillator based on a unique diode nonlinearity effect， offset boosting control and sliding mode control design for global chaos synchronization[J].Journal of Control， Automation and Electrical Systems，2019，30（6）：1-15.

［6］LI W H，BAI G H， HASHEM I M. A new robust finite-time synchronization and anti-synchronization method for uncertain chaotic systems by using adaptive estimator and terminal sliding mode approaches[J].Journal of Control， Automation and Electrical Systems volume，2020，31（5）：1375-1385.

［7］AL-SAWALHA M M.Synchronization of different order fractional-order chaotic systems using modify adaptive sliding mode control[J].Advances in Difference Equations，2020，20（1）：417-425.

［8］CHEN C，LI L X，et al.Finite-time synchronization of memristor-based neural networks with mixed delay[J].Neurocomputing，2017，235（16）：83-89.

［9］ABDURAHMAN A ，JIANG H J，TENG Z D.Finite-time synchronization for memristor-based neural networks with time-varying delays[J].Neural Networks，2015，69（3-4）：20-28.

［10］WANG W P，PENG H P，LI L X，et al.Finite-time function projective synchronization in complex multi-links networks with time-varying delay[J].Neural Processing Letters，2015，41（1）：71-88.

［11］王东晓.分数阶大气混沌系统的比例积分滑模同步[J].天津师范大学学报（自然版），2019，39（5）：35-38.

［12］毛北行，王东晓.不确定分数阶高维混沌系统的自适应滑模同步[J].电子学报，2021，49（4）：775-780.

［13］毛北行.分数阶多混沌系统滑模同步两种方法的比较[J].电子学报，2020，48（11）：2215-2219.

［14］毛北行，王东晓.不确定分数阶Rucklidge系统自适应滑模同步[J].南开大学学报（自然版），2020，53（6）：59-64.

［15］毛北行.分数阶Victor-Carmen系统自适应比例积分滑模同步[J].东北师大学报（自然版），2021，53（1）：43-47.

［16］毛北行.分数阶Victor-Carmen混沌系统的新型滑模同步方法[J].控制工程，2021，28（5）：856-859.

［17］毛北行，王东晓.分数阶不确定R[o]ssler 混沌系统的自适应滑模同步[J].浙江大学学报（理学版），2021，48（2）：210-214.

［18］毛北行，王东晓.金融不确定分数阶混沌系统滑模同步的3种控制方案[J].吉林大学学报（理学版），2022，60（5）：1183-1188.

［19］SPROTT J C.Some simple chaotic flows[J].Physical Review E，1994，52（2）：647-653.

［20］JAFARI S，SPROTT J C.Simple chaotic flows with a line equilibrium[J].Chaos， Solitons amp; Fractals，2013，57：79-84.

［21］梅生伟，申铁龙，刘志康.现代鲁棒控制理论与应用[M].北京：清华大学出版社，2003.

责任编校：刘 燕，田 旭

Two Schemes for Sliding Mode Synchronization of Jafari -Sprott Chaotic System

WANG Dongxiao

（School of Mathematics， Zhengzhou University of Aeronautics， Zhengzhou 450046， China）

Abstract： The sliding mode synchronization problem of Jafari-Sprott chaotic system was studied， and based on Lyapunov stability theory and synchronization control related theories， we had provided research conclusions on synchronization control. Two schemes for implementing synchronization of Jafari-Sprott chaotic system had been proposed. The phase diagram of the attractor and the error curve of the system were drawn using MATLAB simulation technology， and the results obtained were verified numerically to determine the feasibility and effectiveness of the synchronization scheme.

Key words： chaotic system; sliding mode ;synchronization

收稿日期：2023-05-19

基金项目：国家自然科学青年基金（11801528，41906003）

作者简介：王东晓，男，河北威县人，副教授，研究方向为复杂网络与混沌同步。