基于线性优化的移动边缘计算中任务迁移算法的设计与实现

摘 要：移动边缘计算（MEC）是一种可以提高移动端计算速度和安全性的重要技术。用户将移动端任务卸载到附近边缘设备上，以达到减少移动端负载及计算耗能等的效果，如何设计移动端任务在边缘设备中的迁移算法是提高MEC效率的关键问题。文章提出了目前在边缘计算中两种比较普遍的任务迁移算法：整数线性规划[（ILP）]和贪心启发式算法。这两种迁移解决方案除考虑位置、带宽、用户、迁移等方面带来的能量损耗外，还考虑了由于车辆的机动性所带来的损耗，并使用马尔科夫链预测车辆位置，将位置预测和任务迁移相融合。实验结果表明，首先，ILP算法与贪心启发式算法的耗能近乎相同，但在同样耗能的情况下，贪心启发式算法的求解延迟远远小于ILP算法，从而确立了贪心算法在迁移方案中的优势；其次，通过任务刷新频率的选择，可进一步降低贪心启发式算法的耗能，优化后的算法比初始算法耗能降低了约20%。

关键词：ILP；贪心算法；马尔可夫链；刷新频率

中图分类号：TJ760" "文献标识码：A" " " 文章编号：1007 - 9734 （2024） 03 - 0095 - 09

0 引 言

云计算是一种通过网络提供计算服务、存储空间和应用程序的技术，目前已经被广泛应用于金融、教育、医疗、交通等各个领域。云计算为大数据计算等提供了快速计算的条件，但随着大数据时代的发展，各类云计算业务对数据计算的安全性和速度等提出了更高的要求。而目前物联网背景下的数据都较为分散，加上网络带宽的增长速度远远跟不上数据的增长速度，因此，将一部分数据计算卸载到附近的边缘设备而非全在云上执行，即边缘计算就成为当下亟须研究的课题。特别地，在智能车载应用场景，下一代网络支持的车载应用快速增长，其要求连接的车载网络需具备空前的网络容量和严格的服务质量[（]QoS）［1］要求。为了满足这些要求，车载网络应实时支持先进的通信技术和动态数据转发机制，以提高车辆的安全性和使用效率，并减少运输系统的交通拥堵。同时，由于网络带宽不足以完全承担复杂的车载应用，使得边缘计算成为解决这类问题的重要方法。相关研究表明，可以将车载任务转移到附近的边缘网络设备上，以满足车载应用对QoS的严格要求［2］。边缘计算技术可以提升车载应用的服务质量以及用户体验；利用边缘计算的低延迟特点，可以提高车辆应用的响应速度，降低车祸风险。

本文将研究重点放在两种迁移算法（ILP算法和贪心启发式算法）在任务迁移中的时间和空间消耗上。对比两种算法，并对算法进行优化，进一步降低任务迁移所带来的能量损耗。在车载应用中，为了提高车载应用的服务质量以及任务处理速度，主要从最小耗能和最小时间延迟两个方向进行研究。2018年，Tan等［3］提出一种边缘缓存算法并给出了对应的计算方案，利用缓存存储处理信息，同时考虑了车辆的移动特点。[Yousefpour]等［4］研究了任务分流问题，考虑了雾节点间通信和负载共享的优点以最大限度地减少服务延迟，使用[IoT−fog−cloud] 应用程序的通用框架，并提出了一种用于雾功能设备的延迟最小化协作和卸载策略，旨在减少 IoT 应用程序的服务延迟。Jiang等［5］提出了共享雾网络中的延迟感知任务卸载方案，支持延迟敏感、延迟容忍和延迟不敏感等3种类型任务的卸载优化，综合跟踪驱动模拟证明了该方案的有效性。[Tran]等［6］为了最大限度地减少总体服务延迟，研究了任务卸载和资源分配的联合优化问题。黄等［7］在利用SDN网络可配置性的同时，研究了一种车对车（V2V）数据卸载方案，其使用集中式SDN控制器管理两个通信车辆之间的端到端连接。此外，Li等［8］提出了一种基于SDN的移动边缘计算框架，以改善网络的可扩展性和响应时间；Sudip Misra等［9］提出了一种移动感知任务卸载方案Soft-VAN；范艳芳等［10］提出了基于深度强化学习的任务卸载处理，选取一段公路作为实验研究地点，考虑了高速公路的特殊性，讨论车辆之间协同计算的可能性。

综上，现有研究主要围绕能量损耗和时间延迟两个优化方向，很少涉及卸载算法及其性能的对比。本文基于相同仿真环境，比较两个不同的算法所体现出来的性能，从时间和空间上对两种算法进行对比评估，并对优势算法进行进一步的优化。

1 任务卸载系统模型

本文基于分级服务器的车辆网络架构，该网络由一组服务器、链路、车辆以及车辆发送的任务组成，具体如图1所示。

该车辆网络被整体建模为有向图[G=S，L，]其中[S]（Server）和[L]分别表示所有服务器的集合以及服务器之间的链路集合。此外，所有服务器的集合表示为[S=S1， S2，S3，…，Sn]，链接集表示为[L=i，j，∀i，j∈N，i≠j]；网络中的车辆集合表示为[V=V1，V2，V3，…，Vn]；移动端发出任务的集合表示为[J=J1，J2，J3，…，Jn，n∈Z+]；时间步[T∈Z+]。

1.1" 问题描述

图2展现了一个任务迁移场景中车辆网络存在的相关复杂性问题。

首先，利用不同等级服务器和链路搭建边缘网络结构；其次，根据移动车辆［11］当前位置，选择最近的Server进行任务卸载，根据任务活动时间、移动车辆当前位置、移动速度和距当前所在位置最近的服务器，利用马尔科夫链［12］预测车辆移动位置；再次，计算车辆预测移动路径上每一个时间步时刻以及车辆当前位置的最近服务器的位置；最后，根据车辆移动的总时间步数，得到车辆的初始和结束位置。因为每个时间步都会有任务发送，所以车辆的每个时间步的最近服务器都要记录。图2中假设了一个简单的例子，如果任务是从1号服务器开始发送，在4号服务器结束，那么问题就变成了从1点到4点的任务迁移最短路径问题。

综上，本文基于边缘网络［13］算法的研究，建立了服务器、链路、图［14］、移动车辆、任务等实体类，并在这些类的基础上，仿真任务在边缘网络中的迁移，提出两种在目前研究中比较普遍且效果比较好的算法：ILP算法和贪心启发式算法。

1.2" 能量损耗模型

能量损耗由位置损耗、带宽损耗、时延损耗和迁移损耗4个部分组成。

（1）位置损耗（Placement Cost）

一个任务从移动端上传到服务器之后，会根据服务器的不同等级和不同容量，决定该任务的后续迁移、执行情况等。在这个过程中，任务占用服务器的内存，会产生相应的位置损耗，该损耗是4种损耗中占比最大的，位置损耗[ Cplacej]主要是由任务的资源大小决定：

[ Cplacej=Prj×Sci] （1）

式（1）中：[Prj]代表每一个任务在特定服务器位置的资源需求；[Sci]代表在特定服务器位置的单位时间、空间内的能量消耗；i，j分别代表服务器和任务的编号。

（2）迁移损耗（Migration Cost）

迁移损耗[Cmigj]是指任务从特定的服务器之间迁移时所损耗的能量，主要是由链路的容量以及传输速度所决定：

[Cmigj=Mrj×Mli，k∗Lci，k，∀j∈J，∀i，k∈S] （2）

式（2）中：[Mrj]代表每一个任务的预计迁移资源量，[Mli，k]代表当前任务在特定的两个i、[k]服务器之间所有路径中所选择的迁移路径，即所有路径中消耗最小的路径；[Lc]代表选择的迁移路径中，每一条链路的单位资源能量消耗。

（3）带宽消耗（Bandwidth Cost）

带宽消耗[Cbwj]是指在迁移过程中，服务器所产生的能量损耗：

[Cbwj=TP×Sli，k∗Lci，k，∀j∈J，∀i，k∈S] （3）

式（3）中：TP 代表服务器传输吞吐量，不同等级服务器的吞吐量不同，[Sli，j]代表与特定服务器相连的链路，[lci，j]代表链路中每个资源所消耗的能量。

（4）时延损耗（Latency Cost）

时延损耗[Clatencyj]表示当任务出现延迟转发或者延迟上传等问题时，对系统能量损耗所做的惩罚。这里的时延损耗也可以从侧面反映移动端用户的体验，且延时惩罚是根据时间的增长成二次函数增长。

[flag=latency−req] （4）

[Clatencyj= 0，" " " " " if flaglt;0" Rm∗r，" "if flaggt;0] （5）

式（4）和式（5）中，设置flag来计算延迟是否达到惩罚阈值；latency代表当前任务已经在迁移中产生的延迟，是当前的真实值；req代表每个任务的延迟阈值，如果超出这个范围则开始计算惩罚；[Rm]代表算出的实际的延迟和设置好的预计延迟的差值；r代表每延迟1ms所造成的能量惩罚。

综上，在任务迁移过程中的总延迟：

[Cmigj+Cplacej+Clatencyj+Cbwj] （6）

在考虑能量损耗的同时，本文还考虑了在最小耗能前提下的时间损耗的设置，根据任务的大小及在服务器之间转移的速度，设置转移延迟及任务等待延迟，用于测算算法在时间延迟上的表现。

2 迁移算法设计

本研究是以最小耗能为目标，因此，结合上述4种能量损耗，设置目标函数、相关约束、迁移过程中任务的路径以及迁移过程中出现的误差，列出线性规划求解方程如下：

[MinimizeCmigj+Cplacej+Clatencyj+Cbwj] （7）

s.t[" Ejksi=Ljksi，∀si∈S，∀jk∈J] （8）

[ si（qsi+gsi）×pljii≤Rsi（ram， cpus， tor），∀ si∈S，∀ jk∈J] （9）

[j∈Jjr xji，k+j∈Jj'r xjk，i≤Ci，k， ∀（i，k）∈] [L，j∈J] （10）

[STvjk=1，EDvjk=1，Du≤Ulr] （11）

式（8）表示每个任务进出服务器所要消耗的能量是相同的，即每个任务进出服务器所带来的带宽损耗是相同的，[Ejksi]表示任务[jk]退出服务器[si]的能耗，[Ljksi]表示任务[jk]进入服务器[si]的能耗；式（9）表示任务在服务器中所占的容量不能超过服务器本身的可用资源容量上限；由于一条链路的迁移是双向的，即可以从[i]传到[k]，也可以从[k]传到[i，]所以式（10）表示所有正反方向的迁移所消耗资源之和，不超过链路本身预设的资源最大值；式（11）表示任务只能分别访问一次初始服务器和结束服务器，并且总延迟不能超过用户延迟需求，如果任务实际总延迟大于所预设的延迟，则任务直接刷新［15］。其中，[gsi]代表任务所在位置是否在服务器内部，[qsi]代表如果任务在服务器内部那么任务的迁移是否已经发生，[q，g]这两个变量都是bool变量，当[qsi]=0时 [q+g]=0：

[qsi+gsi=0 代表任务不在服务器内部qsi+gsi=1 代表任务在服务器内部] （12）

如果任务在服务器的内部，则所有任务的位置资源不应该超过当前服务器的最大容量。服务器资源类别分为3种，RAM（内存），CPU（CPU核数）及STORE（硬盘容量）。式（10）表示从[i，k]两个服务器的连线中迁移的总容量小于链路容量，定义[xji，k]为是否选择[i，k]两个服务器之间的链路当作迁移链路：

[ xji，k=0 表示当前链路不被选择 xji，k=1 表示当前链路为任务迁移链路] （13）

为了将计算任务从服务器节点下载到车辆，需要选择最佳路径，以使迁移能量损耗最小。此外，在选择迁移路径时，还需要考虑车辆的机动性。文献［16］证明了k阶马尔可夫预测变量可用于预测移动节点的位置，利用车辆的已知信息对车辆行动进行预测。本文采用类似的方法来预测车辆在网络中的位置。首先预测在下一个时间步内将发生服务器位置转换的概率；再根据马尔可夫链生成用户在每个时间步中每个服务器上计算的概率，以及一定时间后用户所在的位置来更新马尔可夫链［14］；最后预测经过时间t之后的车辆将从现有位置移动到位置s的条件概率。

因此，对于给定的位置信息c和经过时间t，每辆车在Δ时间内移动到每个可能位置s的概率计算如下：

[P（s∣c，t）=P（s）PS（t⩽zlt;t+Δ∣c，t）] （14）

式（14）中，P（s）代表每个可能位置s的转移概率，可以通过式（15）计算：

[Pst+Δ=s|H≈Pst+Δ=s|H=Ncs，HNc，H] （15）

式（15）中，N（s，H）代表运动历史集H中特定位置s的出现次数，N（[c]，H）代表所有位置的出现次数。在t+Δ时间内最有可能到达的位置s可通过式（16）表示的最大化概率得到：

[st+Δ= argmaxPst+Δ=s ] （16）

研究服务器与移动端在每个特定时间步下的位置关系，将车辆的移动性融合ILP问题，并对问题进行求解。

3 卸载迁移算法优化

3.1" 贪心启发式算法

为解决最小耗能问题，除了上述ILP算法，还可以用贪心启发式算法来找寻全局最优解。首先确定服务器两两之间迁移所需的最小耗能，根据这些最小耗能组成一个路径图。然后再根据[dijkstra]最短路径图算法，在这个新组成的路径图中，找到两个特定服务器节点之间的最小耗能。

相对于ILP算法，贪心算法以少量的结果准确性丧失为代价，提升了算法的简洁程度。贪心启发式算法的流程如算法1所示。

算法的输入中，[Vi，j]代表的是在系统中存在哪些链接的二进制指示。初始节点和结束节点的设置依赖时间步和当前服务器位置表示为[Cvs，t，]其中[，s]代表服务器位置。如果任务刚好不在任意一个服务器的位置或者初始化结束时期，则[s=] -1；[t]代表时间步，当任务初始化时，[t=] -1，当[t]等于任务活动时间的[Vt]时（[Vt]代表任务迁移前就设置好的任务活动时间，如果任务迁移超过这个时间，任务刷新），任务迁移结束。[j]代表当前迁移任务，[Ei，jmin]代表任意两个服务器[i，j]之间的权重边，即路径的最小耗能。这里服务器之间的最小耗能在[Cmigj+Cplacej+Clatencyj+Cbwj]基础上，增加计算每条可能路径需要的能耗，故整体耗能的计算为：

[Cmigj+Cplacej+Clatencyj+Cbwj+Cposj] （17）

式（17）中，[Cposj=Lg∗Ccal]，其中[Lg]代表每个特定服务器所有连线的平均值，可用于计算任务的迁移预期；[Cposj]代表计算预期迁移路线的能量损耗。先计算出每两个服务器之前迁移的能耗，求出[Ei，jmin=minEi，j]，并利用[Ei，jmin]和所有服务器集合，组成一个带权无向图，用于计算耗能最小的迁移路径。

[算法 1：贪心启发式算法

1. 初始化[visit][]， [dist][]，[ path][]

2. for [j in J ]

3.[" for i，j in S ]

4. if [Vi，j=1] 根据式（17）计算路径消耗[Ei，j]

5. [Ei，jmin=agmin（Ei，j）]

6. for [i in S]

7. [ min_cost=max]

8. [for j in S]

9. if[ visitj==1] amp;[ dist][[j]]lt;[min_cost]

10. [min_cost=dist[j]]

11. [index=j]

12. [ visit[index]=true]

13. 更新[ dist[] and path[]]

14. 重复步骤6～13直到计算完成 ]

最短迁移路径可使用[dijkstra]算法求解得到，不断修改更新当前最短路径，找到对于每个任务j的最小耗能迁移路径。算法的输出是最短路径中经过的所有节点的列表以及最小耗能的数值。在算法最后，需要更新全局资源和最短路径中的资源占用情况。当任务迁移完成后，以当前任务的开始节点、结束节点和路径上的途径节点为依据，删除该路径中特定迁移任务j的资源占用，以持续支持后续任务的迁移，同时清零最短路径列表、开始节点、结束节点、预计迁移耗能等。

3.2" 刷新频率优化

上述贪心启发式算法的复杂度取决于以[OF]复杂度运行的服务器节点，以及基于Dijkstra的最短路径算法复杂度[OR+F2] ，故部分算法复杂度为[OF+（R+F2）]≈[OR+F2]；另一方面，算法包括位置预测和路径选择，k阶马尔可夫预测变量在[Ok2]中运行，其中k是车辆位置的输入序列数［17］。贪心启发式算法的复杂度方案为[Ok2+（R+F2）]，其中k的值由用户移动端来决定，刷新频率优化算法如算法2所示。

[算法2：刷新算法

1.初始化[Cvs，t]，[ Lv]，[ jk]，[ SS， SE]，[ fresh]

2. for [t in T ]

3.[ for j in J ]

4. [refresh=j_fresh1] 根据任务是否到达刷新间

5. [if fres]h

6. 更新服务器移动端在任务中的存储

7.[" startnode=currentnode]

8. 根据式（17）更新[costgraph]

9. 重复步骤3～8直到计算完成 ]

算法2的重点在于任务在迁移过程中的刷新频率［15］，在任务设计中加入刷新标志和刷新频率，其中T代表最大时间步，表示每个时间步进行一次任务刷新。首先利用时间步遍历所有任务，根据任务记录，查找当前移动端位置和任务位置，并查找任务是否达到刷新时间（在初始算法中，因为从任务迁移开始到任务迁移结束不进行刷新，所以默认刷新频率是T，即等到任务迁移结束才进行刷新）。如果达到，根据车辆预测位置，更新马尔可夫链预测矩阵，并更新资源和初始点位置（这里的初始点指的是贪心算法中，算法求解从初始点到结束点的最小耗能路径），然后根据现有的初始位置，保留之前算法中当前点与结束点之间的最短耗能路径，并重新计算不同迁移路线的耗能及更新链路所需的耗能，算出更新后的算法选择路径与更新前对比，如果相同则继续，如果不同则更新路径。

4 仿真环境

4.1" 参数设置

相关参数设置包含以下几类。

（1）任务（Job）

任务是迁移算法设计的重点。当前边缘计算已支持视频图片等多源异构的数据格式及对应的差异化资源需求。定义[Jtype]代表任务类型；将任务与移动用户端关联，定义任务所需资源，[Rp]，[RBW]，[RM]分别代表位置所需资源、带宽所需资源和迁移所需资源；定义任务时间长度[LJ]以衡量任务活动时间（活动时间内任务处于活跃状态，可以迁移）；定义任务刷新标志[Rf]，根据移动端所在位置和任务时间长度状态，判断任务是否需要刷新；定义任务刷新频率[Rt；]定义任务延迟需求[LR]；定义变量[FS，Ea，b， a，b∈0，1，]对任务是否经过开始和结束节点进行检测。

（2）服务器（Server）

服务器是在任务迁移过程中的主要任务运行环境。通常把服务器分为三级，第一级与第二级属于边缘网络，第三级属于云端。云端和边缘网络的区别在于云端的容量和处理能力都趋近于上限。本文用[SL]代表所设置服务器的级数；用[SB]代表当前服务器所在位置的限制；定义服务器可用资源[SR]用于监测在每个特定时间步服务器的可用资源容量，设置服务器[Rc]代表每一个位置资源所消耗的服务器能量，根据两者可计算出任务迁移时服务器的能量消耗。

（3）链路（Link）

对于边缘计算网络，不同级别服务器之间的迁移需要有所限制，高级服务器不应向低级服务器传输数据。定义[TL∈（0，1）]以限制服务器之间的迁移路径，[TL=0]表示此迁移方向可以进行传输，反之则不能传输。链路所储存的信息，有些和服务器所储存的信息类似，定义[LI]代表在服务器中记录的链路；定义 [Li，j ，i，j∈S] 代表保存特定服务器之间的路径；定义[Pi，j]为存储特定服务器之间的所有路径数以及路径资源。此外，链路还需要定义链路资源限制[RL]，定义[VL]为活动链路记录，记录当前边缘迁移网络中哪些链路是正在使用的。同时，低等级服务器应主动向高等级服务器转发，因此定义[DL1，L2]记录低等级服务器与高等级服务器之间的最短迁移距离，其中[L1，L2]代表服务器的不同等级。在维护不同等级服务器之间的链路时，也需要控制同等级之间的链路数量，从而避免链路过多消耗内存。定义[LP为]限制同等级服务器之间的链路条数；定义[Ra]为当前链路可用资源，用于计算任务是否可以迁移；定义[DS]为交换服务器时产生的延迟。

（4）移动端（User）

移动端的主要任务是发送任务，考虑采用马尔可夫链预测增加移动端移动的真实性。移动端定义多种类型的移动形式，如步行、车载等，不同形式的移动端的移动速度也有一定差异。同时需要用户部分定义相关查找函数，用于查找最近服务器，该函数将移动端当前位置与服务器位置相结合，将本来随机性强的车辆自主移动变为有路线的服务器位置的移动。根据这个函数，定义[UV]代表移动端所有可能移动的拓扑图，并根据[UV]得到移动端相对于任务所在当前服务器可能移动到的下一个服务器的概率以及位置信息，用于移动端的位置预测。每次选取概率最大的位置得出的路线图[Uvt]来定义移动端真实移动路径，并利用真实移动路径图不断更新[UV]、[Uvt]，同时更新移动端位置。基于马尔可夫链生成用户在每个时间步中每个服务器上计算的概率，并根据用户在特定位置经过特定时间量[Tk]（k代表k个时间步）之后的位置更新预测矩阵P。其中，s是预测矩阵的纵轴，代表服务器个数；t代表时间步。矩阵P表征在特定时间步下，当前任务迁移到不同服务器的可能性。同时在行动预测中，要对移动端位置进行修正，如果移动端位置超出网络设置预期，需要修正移动端方向，并降低移动端最大速度，重新设定速度限制[Sm]。在移动端移动过程中，根据[Lm]（即车辆的位置，用x，y坐标表示）调整车辆转动角度。由于移动端和任务联系紧密，所以定义变量[Uid]作为用户id，并且在设置任务相关变量时，也用[Uid]作为任务的一个标志，融合移动端及任务表示。

（5）图（Graph）

图是联合上述部分的一个重要模块，其作用主要是形成邻接矩阵。利用二进制矩阵的方式表示两点之间的路径，将链路设置成边，将服务器设置成节点，将经过链路所需要消耗的能量设置成边的权重，并定义一些基础函数，用于获取两节点之间所有的现有路径。文中所提到的平均路径数、增加或者删减特定边、更新权重数据，其用途都和上述几个模块所提到的功能相关联，是实现上述模块所描述函数的基础。定义向量为最短路径储存，根据[dijkstra]算法，不断更新变量，将路径长度替换成迁移所需要消耗的能量，形成一个带权无向图，在图中求两点之间最短距离，即映射两点之间的最小迁移耗能问题。

仿真环境的主要参数名称及含义如表1所示。

4.2" 仿真环境设置

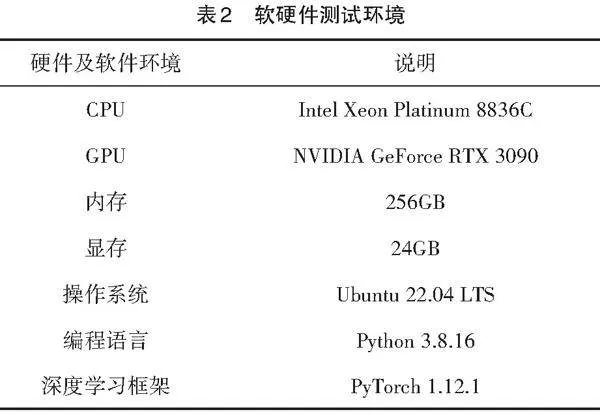
实验环境基于python，设置用户延迟需求为0.2 ms，每个服务器向同等级服务器的链路限制[Lp]为6。设置三种不同任务迁移延迟需求范围为（0.25 ms，0.40 ms），任务时间步长度为10。这里简化复杂程度，将任务长度[Lj]设置为总时间长度，通量设置为（0.2 mb/s，0.4 mb/s），任务大小（任务位置资源需求）设置为8GB内存，2GB RAM。服务器设置方面，设置三级服务器1个，二级服务器2个，一级服务器5个（三级为最高级）。服务器资源方面，二级服务器资源：CPU6核， 3000 GB内存，8GB RAM；一级服务器资源：CPU4核，1000 GB内存，4GB RAM。链路方面，与同等级链路[Lp]与上面设置相同，转换延迟为[DS]=300 ×10-3 ms，每1 m链路传输所需要的时间延迟为60×10-3 ms，移动端的用户数量为4，移动端车辆最大速度[Sm]= 2.5m/s，移动端可能路径集合U= 30，刷新参数[Rt]= 10。实验的软件环境参数如表2所示。

5 实验结果

本实验对ILP算法和贪心启发式算法进行比较，在参数设置相同的情况下对比两种算法空间/时间的效率，并调整参数，研究不同参数对算法产生的差异化影响。

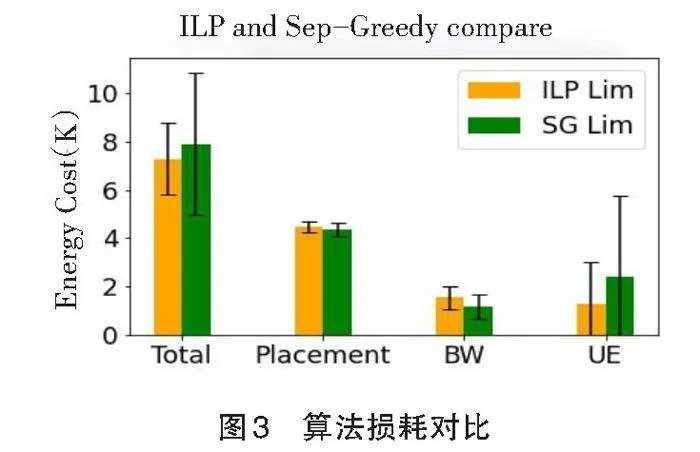
图3为采用4.2节参数设置时，贪心算法和ILP算法的能量消耗。重复运行实验10次，并存储每个ILP和SG模型的成本数据，取10次的平均值，并标明结果浮动范围。其中，Placement为位置资源能耗，BW包括迁移能耗和带宽能耗，UE为延迟能耗。从图中可以看出，两种算法的耗能相近，在调整链路资源后，迁移耗能增大，用户延迟总体降低。

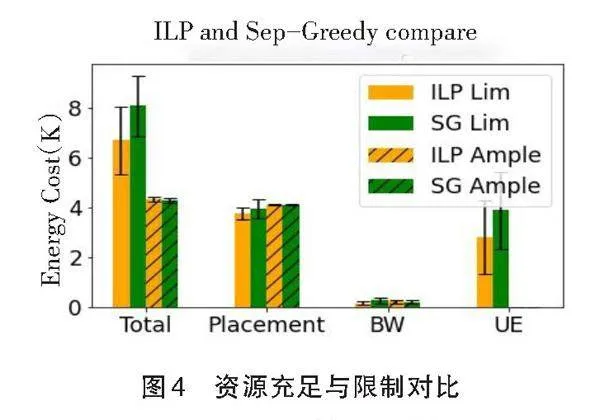
图4为在资源设置是否充分形况的能量消耗。

重复实验10次，分别计算ILP算法和贪心算法的成本数据并取平均值，同时标明结果浮动范围。图4中，阴影柱表示链路资源和服务器资源完全充足（不会产生等待延迟，并且多个任务可以在链路中一起传输）。可以看到，在资源限制的情况下，能量消耗、传输和位置资源的比例与图3中相近，用户等待延迟受资源充足与否的影响较大，总体差距主要体现在等待延迟这一对比指标上。

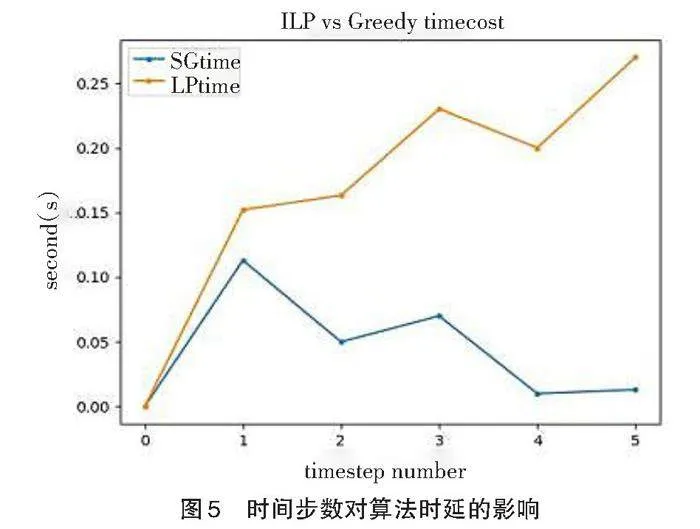
根据上述实验结果，ILP算法和贪心算法对于迁移任务来说耗能相近，改变链路参数和移动端参数对结果无显著影响。在最小能量消耗的基础上，设置仿真环境固定的时间延迟，在三级服务器个数为0、二级服务器个数为1的情况下，分别改变时间步、移动端个数以及服务器个数，评估ILP算法和贪心算法的延迟。如图5所示，在时间步数改变的情况下，ILP算法的运行时延随着时间步的增加而增加，而贪心算法的延迟则能保持稳定。

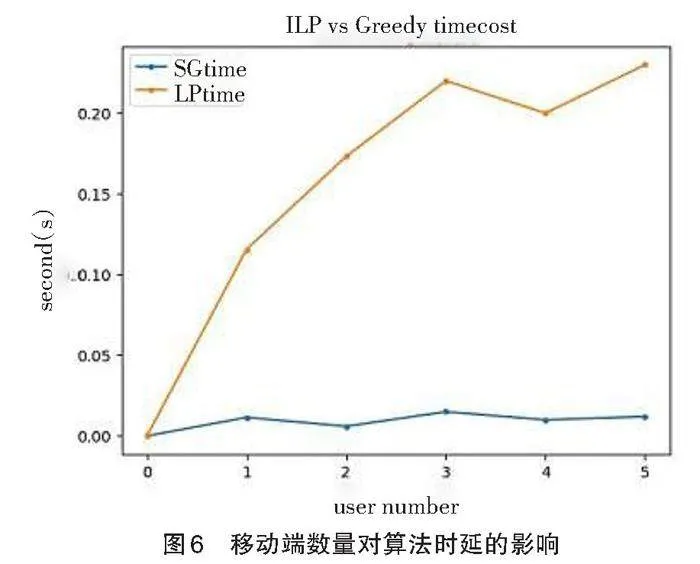
除了时间步数以外，移动端的数量在算法中也占有重要地位。在其他参数相同的情况下，随着移动端数量的增加，ILP算法的约束条件也会增加很多。如图6所示，对移动端数量做出调整并训练10次取平均值，ILP算法的时间延迟为0.243s，贪心算法为0.012s。可见在移动端数量增加的情况下，ILP算法的计算时延远远超过了贪心算法，贪心算法在环境变化的情况下表现得更加稳定。

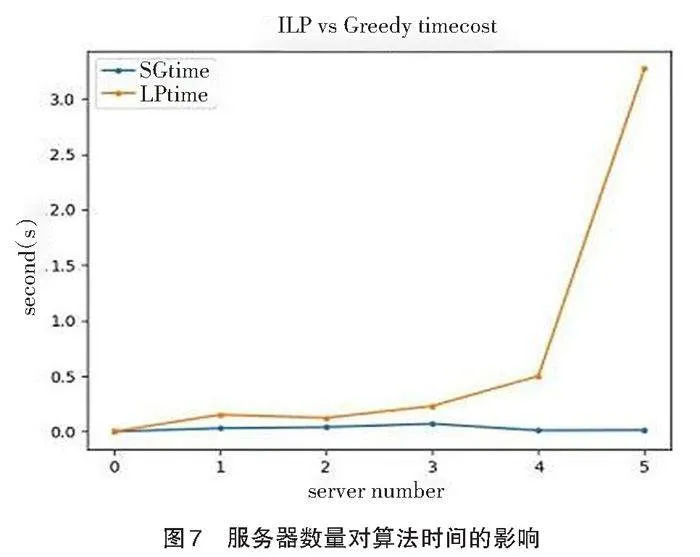
服务器数量对算法时间也有很大影响，如图7所示。

由图7可以看出，随着服务器数量的增加，贪心启发式算法的运行时间一直保持平稳，而ILP算法的时延已经呈指数级增长。ILP算法在服务器增加的情况下很难有效地承担负载，其算法时延随服务器数量增加而迅速增长，而贪心算法可有效应对更高负载、更多服务器情况下的边缘计算任务卸载。

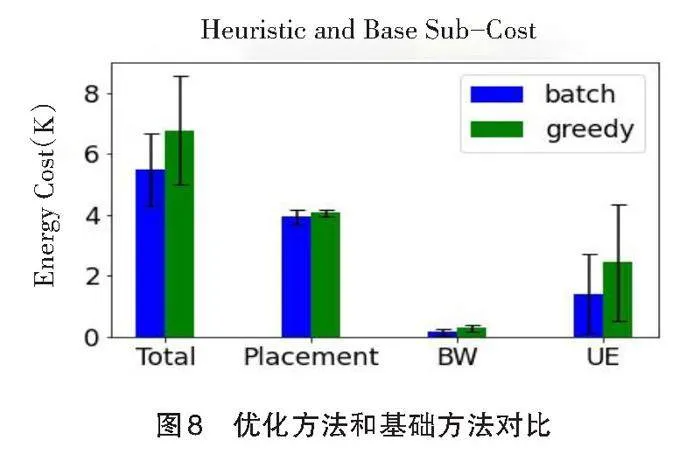
综上，在任务卸载过程中，贪心算法相对于ILP算法的优势明显。进一步地，通过调整刷新频率不断更新算法，可讨论不同刷新频率对应的能量消耗。利用上文提到的刷新思路对贪心算法进行优化，对比不同刷新速度下的算法耗能，确定最优刷新频率为每秒2次。如图8所示，刷新优化后的贪心算法在各个方面的能量损耗均有所下降，平均降低了20%左右。

6 结 论

本文主要研究分析了边缘计算任务迁移过程中使用的ILP和贪心启发式两种算法。通过搭建仿真环境，模拟了移动端在一个二维固定广度内的迁移过程，并对比了两种算法的性能。研究发现，在同样的仿真环境下，两者的耗能相近；在耗能相同的前提下，分别通过调整服务器数量、时间步长度、移动端数量等来对比算法时延，确定了贪心算法的优势。进一步通过调整任务刷新频率对算法进行优化，减少了贪心算法约20%的额外耗能。

参考文献：

［1］陈清林，邝祝芳.基于DDPG的边缘计算任务卸载和服务缓存算法［J］.计算机工程，2021，47（10）：26-33.

［2］李智勇，王琦，陈一凡，等.车辆边缘计算环境下任务卸载研究综述［J］.计算机学报，2021，44（5）：963-982.

［3］TAN L T，HU R Q.Mobility-aware edge caching and computing in vehicle networks：a deep reinforcement learning［J］.IEEE Transactions on Vehicular Technology，2018，67（11）：10190-10203.

［4］YOUSEFPOUR A，ISHIGAKI G，GOUR R，et al.On reducing iot service delay via fog offloading［J］.IEEE Internet of Things Journal，2018，5（2）：998-1010.

［5］JIANG Y X，TSANG D H K.Delay-aware task offloading in shared fog networks［J］.IEEE Internet of Things Journal，2018，5（6）：4945-4956.

［6］TRAN T X，POMPILI D.Joint task offloading and resource allocation for multi-server mobile-edge computing networks［J］.IEEE Transactions on Vehicular Technology，2019，68（1）：856-868.

［7］HUANG A T，NIKAEIN N，STENBOCK T，et al.Low latency MEC framework for SDN-based LTE/LTE-a networks［C］//2017 IEEE International Conference on Communications（ICC），2017：1-6.

［8］LI M，SI P B，ZHANG Y H.Delay-tolerant data traffic to software-defined vehicular networks with mobile edge computing in smart city［J］.IEEE Transactions on Vehicular Technology，2018，67（10）：9073-9086.

［9］MISRA S，BERA S.OFT-VAN：Mobility-aware task offloading in software-defined vehicular network［J］.IEEE Transactions on Vehicular Technology，2020，69（2）：2071-2078.

［10］范艳芳，袁爽，蔡英，等.车载边缘计算中基于深度强化学习的协同计算卸载方案［J］.计算机科学，2021，48（5）： 270-276.

［11］梁广俊，王群，辛建芳，等.移动边缘计算资源分配综述［J］.信息安全学报，2021，6（3）：227-256.

［12］陈强.面向5G网络的MEC关键技术与实现分析［J］.数字通信世界，2021（5）：5-8.

［13］李卓，宋子晖，沈鑫，等.边缘计算支持下的移动群智感知本地差分隐私保护机制［J］.计算机应用，2021，41（9）： 2678-2686.

［14］李沁颖，曹青松.基于马尔科夫优化的移动边缘计算车载网络任务卸载［J］.济南大学学报（自然科学版），2021，35（6）：540-545.

［15］ROSSI F L，NAGANO M S.Heuristics and iterated greedy algorithms for the distributed mixed no-idle flowshop with sequence-dependent setup times［J］.Computers amp; Industrial Engineering，2021，157：107337.

[16]PANG Y，WU J G，CHEN L，et al.Energy balancing for multiple devices with multiple tasks in mobile edge computing[J].Journal of Frontiers of Computer Science and Technology，2022，16（2）：480-488.

［17］LI W，JIN S F.Performance evaluation and optimization of a task offloading strategy on the mobile edge computing with edge heterogeneity［J］.The Journal of Supercomputing，2021，77（11）：12486-12507.

责任编校：刘 燕，田 旭

Design and Implementation of Task Offloading Algorithm in Mobile Edge Computing Based on Linear Optimization

SHEN Xin1，YE Yuhao2，SI Yingli3， 4

（1. The First Air Force Armament Department Representative's Office in Luoyang， Luoyang 471009， China；

2. Xi’an Jiaotong University， Xi’an 710049， China；

3. China Airborne Missile Academy， Luoyang 471009， China；

4. National Key Laboratory of Air-based Information Perception and Fusion， Luoyang 471009， China）

Abstract： Mobile Edge Computing （MEC） is an important technology that can improve the computational speed and security of mobile devices. Users offload mobile tasks to nearby edge devices， reducing the load on the mobile devices and decreasing computational energy consumption. The task migration algorithm in edge devices is a key issue for enhancing task processing efficiency. This paper proposes two commonly used task migration algorithms in edge computing： Integer Linear Programming （ILP） and Greedy Heuristic algorithm. Both migration solutions consider location loss， bandwidth loss， user loss， and migration loss. Additionally， the solutions for task migration need to consider not only parameters related to energy consumption but also vehicle mobility. This paper utilizes a Markov chain to predict vehicle locations and integrates location prediction with task migration. The experimental results show that ILP and Greedy Heuristic algorithm have nearly the same energy consumption. However， under the same energy consumption， the Greedy Heuristic algorithm exhibits significantly lower time delay compared to the ILP algorithm， establishing the advantage of the Greedy algorithm in the migration scheme. Furthermore， by selecting the task refresh frequency， the energy consumption of the Greedy Heuristic algorithm can be further reduced. The optimized algorithm reduces energy consumption by approximately 20% compared to the initial algorithm.

Key words： ILP; Greedy algorithm; Markov chain; refresh frequency

收稿日期：2024-02-20

基金项目：航空科学基金项目（2023Z004012001）

作者简介：沈 欣，男，浙江杭州人，工程师，硕士，研究方向为导航制导与控制。

*通讯作者：司迎利，男，甘肃静宁人，高级工程师，硕士，研究方向为导航制导与控制。