非线性BBMB方程能量稳定有限元方法高精度分析

摘 要：文章主要研究非线性 Benjamin-Bona-Mahony-Burgers（BBMB）方程的能量稳定全离散有限元格式的高精度分析。首先，证明了后向Euler全离散格式的能量稳定性，得到了[H1]模意义下有限元解的有界性。其次，利用上述有界性和Brouwer不动点定理证明了离散问题解的存在唯一性。再次，利用协调双线性元的特殊性质，得到了相应的超逼近和整体超收敛结果。最后，通过数值试验验证了理论分析的有效性。

关键词：BBMB 方程；能量稳定格式；超逼近和超收敛分析

中图分类号：O242.21" "文献标识码：A" 文章编号：1007 - 9734 （2024） 03 - 0108 - 05

0 引 言

非线性偏微分方程如 Navier-Stokes 方程、反应扩散方程、KdV方程等，可以用来描述许多自然现象和工程技术问题。BBMB方程是非线性偏微分方程的一种，它结合了Benjamin-Bona-Mahony（BBM）方程和Burgers方程的特点。其中， BBM方程可以用来描述长波在浅水层或等离子体中的传播，Burgers方程则用来描述非线性扩散过程。因此，BBMB方程可用于描述具有非线性色散和耗散效应的物理系统。

本文考虑如下的BBMB方程：

[ut-αΔut-βΔu=∇⋅f（u）， （X，t）∈Ω×（0，T]u（X，t）=0， （X，t）∈∂Ω×（0，T] u（X，0）=u0（X）， X∈Ω] （1）

其中，[Ω∈R2]为开有界凸多边形区域[，]边界记为[∂Ω][；][ X=（x，y）；" αgt;0， βgt;0；][ 0lt;Tlt;∞；][" f（u）=（12u2+u，12u2+u）]；[Δ 和 ∇⋅]分别表示二维拉普拉斯算子和散度算子；[u0（X）]是已知的光滑函数。

关于BBMB方程，由于其非线性性质，真解往往很难求出，故近年来人们越来越多地专注于其数值模拟方法的研究，如有限差分法［1-3］、有限元法［4-5］、无网格法［6］等。在这些方法中，有限元法被认为是求解偏微分方程的重要方法。然而，对于BBMB方程，目前大多数的研究只关注于一维情况下的收敛性，对二维情况下的超收敛分析还很少涉及。

众所周知，能量稳定的数值方法既可以保证数值解的稳定性又能防止数值振荡。这种方法有助于提高计算的准确性和可靠性，也适合模拟具有长时间特性的非线性问题。针对BBMB方程，目前大多数的能量稳定格式都是基于有限差分方法，关于该方程的能量稳定有限元方法，还少有报道。

此外，在求解非线性偏微分方程时，有限元解在某一种模意义下的一致有界性在收敛和超收敛分析中起着至关重要的作用［7-10］。例如，文献[7]采用数学归纳法得到了[W1，∞]模下数值解的有界性；文献[8]利用误差分裂技术给出了[W0，∞]模下近似解的有界性。随后，上述两种方法被应用于各种非线性偏微分方程（见文献[9-10]等）。本文通过对离散格式能量稳定性的证明，得到了模意义下有限元解的有界性，所采用的方法较以往文献更为简单、直接。

基于以上思想，本文的主要目的是建立方程（1）能量稳定的向后Euler全离散格式，并研究其超逼近和超收敛误差估计。后面的安排如下： 第二部分引入了有限元空间和向后Euler全离散格式，然后证明了该离散格式的能量稳定性和[H1]模意义下数值解的有界性；第三部分证明了该离散格式解的存在唯一性；第四部分利用协调双线性元的高精度性质，得到了[H1]模意义下的超逼近和超收敛结果；最后给出数值算例说明方法的有效性。

1 有限元空间构造和能量稳定格式

令[Wk，p（Ω）]为标准的Sobolev空间，其范数为

[vWk，p（Ω）=（|m|≤kΩ|Dmv|pdX）1p， 1≤p≤+∞max |m|≤kess supX∈Ω |Dmv|， p=+∞ ]

和[HK（Ω）=Wk，2（Ω）， H0（Ω）=Lk，2（Ω），]其中[dX=dxdy]。

接下来我们引入带时间的Sobolev空间的定义[11]。

[Wk，p（t1，t2；Φ）={v：‖∂mv∂tm（⋅，t）‖Φ∈Lp（t1，t2），0≤m≤k，1≤p≤+∞}，]其上的模定义为

[‖v‖Wk，p（t1，t2；Φ）=（m=0kt1t2‖∂mv∂tm‖pΦdt）1p，1≤plt;+∞max0≤m≤kesssupt∈[t1，t2]‖∂mv∂tm（⋅，t）‖Φ，p=+∞ ]。

令[Ω]是一个边界平行于坐标轴的多边形区域，[Th]是[Ω]的一个矩形剖分，不需要满足正则性条件[11]。" "对任意的[ K∈Th，hK=diamK，h=maxK∈ThhK]，定义如下的协调双线性有限元空间[Vh]：

[Vh={vh∈H10（Ω）：vh|K∈span{1，x，y，xy}，vh|∂Ω=0，∀K∈Th}，]相应的插值算子定义为[Ih：v∈V=H10（Ω）→Ihv∈Vh]。

则方程（1）的变分形式为：求[u∈V]，使得

[（ut，v）+α（∇ut，∇v）+β（∇u，∇v）=-（f（u），∇v），∀v∈Vu（X，0）=u0（X）] （2）

令[{tn|tn=nΔt ；n=0， 1，…，N}]为[[0，T]]上的一个剖分，时间步长定义为[Δt=T/N]。对任意的[[0，T]]上的函数[u]，定义[un=u（X，tn），∂tun=un-un-1Δt]，则形式（2）的向后Euler全离散格式为：求[Unh∈Vh]，使得

[（∂tUnh，vh）+α（∇∂tUnh，∇vh）+β（∇Unh，∇vh）=-（f（Unh），∇vh），∀vh∈VhU0h=Ihu0（X）] （3）

我们有如下的能量稳定性和有界性。

定理1 设[Unh]为格式（3）的解，[En=‖Unh‖20+α|Unh|21（n=0，1，…，N）]为离散能量，有

[En≤En-1" （ n=1， 2，…，N）] （4）

特别地，

[‖Unh‖1≤K" （ n=1， 2，…，N）] （5）

其中，[K=max{1，α}min{1，α}‖U0h‖1。]

证明：在格式（3）中令[vh=Unh]，则有

[（∂tUnh，Unh）+α（∇∂tUnh，∇Unh）+β（∇Unh，∇Unh）]

[=-（f（Unh），∇Unh）] （6）

易知

[（∂tUnh，Unh）≥12Δt（‖Unh‖20-‖Un-1h‖20）] （7）

[α（∇∂tUnh，∇Unh）≥α2Δt（|Unh|21-|Un-1h|21）] （8）

且非线性项可化为

[-（f（Unh），∇Unh）" " " " =Ω（12（Unh）2+Unh）[（Unh）x+（Unh）y]dxdy=Ω12（Unh）2[（Unh）x+（Unh）y]dxdy+" " " " " " " " " " " ΩUnh[（Unh）x+（Unh）y]dxdy" " " " " " " " " " " " " （9）]

利用Green公式以及[Unh|∂Ω=0]，可得[Ω（Unh）2[（Unh）x+（Unh）y]dxdy" " " " " " " "=-Ω（Unh）[2Unh（Unh）x+2Unh（Unh）y]dxdy+∂ΩUnh（Unh）2⋅（nx+ny）ds =-Ω2（Unh）2[（Unh）x+（Unh）y]dxdy，]

其中，[n=（nx，ny）]为边界上外法向量，故

[Ω（Unh）2[（Unh）x+（Unh）y]dxdy=0] （10）

同理，

[ΩUnh[（Unh）x+（Unh）y]dxdy=0] （11）

将式（10）和式（11）代入式（9），我们有

[（f（Unh），∇Unh）=0] （12）

由式（7）、式（8）及式（12）可知，有如下式子成立：

[12Δt[（‖Unh‖20-‖Un-1h‖20）+α（|Unh|21-|Un-1h|21）]≤0] （13）

故[En≤En-1]，（4）式得证。

最后，（13）式两边同时乘以[2Δt]，并关于[n]求和，可得

[min{1，α}‖Unh‖21≤max{1，α}‖U0h‖21，]

令[K=max{1，α}min{1，α}‖U0h‖1]，则（5）式成立，结论得证。

2 能量稳定格式解的存在唯一性

本节我们主要给出格式（3）解的存在唯一性。

引理1[[12]] 已知 H 是一个有限维Hilbert空间，内积和模分别定义为[（⋅ ，⋅）H]和[‖⋅‖H]，[F：H→H]是一个连续映射，若对任意的[ϑ∈H]且[‖ϑ‖H=kgt;0]时，成立[（F（ϑ），ϑ）H≥0]，则存在[ϑ*∈H]且[‖ϑ*‖H≤k]使得[F（ϑ*）=0]。

定理2 设[U0h，U1h， … ，Un-1h]已知，则存在唯一的[Unh]满足格式（3）。

证明： 首先，我们给出如下的存在性证明。定义如下的映射[F：Vh→Vh]满足

[[（F（ϕ），qh）=（ϕ，qh）+α（∇ϕ，∇qh）+βΔt（∇ϕ，∇qh）]

[+Δt（f（ϕ），∇qh）-（Un-1h，qh）-][α（∇Un-1h，∇qh），∀ϕ]，

[qh∈Vh]] （14）

容易验证[F]是连续映射。

在式（14）中令[qh=ϕ]，注意到[（f（ϕ），∇ϕ）=0]，则有[（F（ϕ），ϕ）=（ϕ，ϕ）+α（∇ϕ，∇ϕ）+βΔt（∇ϕ，∇ϕ）+Δt（f（ϕ），∇ϕ）-（Un-1h，ϕ）-α（∇Un-1h，∇ϕ） ≥min{1，α}‖ϕ‖21-（Un-1h，ϕ）-α（Un-1h，ϕ） ≥min{1，α}‖ϕ‖21-‖Un-1h‖0‖ϕ‖0-α‖∇Un-1h‖0‖∇ϕ‖0 ≥min{1，α}‖ϕ‖21-（1+α）‖Un-1h‖1‖ϕ‖1 ≥‖ϕ‖1（min{1，α}‖ϕ‖1-（1+α）‖Un-1h‖1） ，]

令[|ϕ‖1=1+αmin{1，α}‖Un-1h‖1+1]，则有[（F（ϕ），ϕ）≥0]。由引理1可知存在[ϕ*∈Vh]使得[F（ϕ*）=0]，显然，[Unh=ϕ*]即为所求，则存在性得证。

其次，我们证明唯一性。

假设[Un1]和[Un2]分别为格式（3）的两个解，令[Un=Un1-Un2]，则有

[（∂tUn，vh）+α（∇∂tUn，∇vh）+β（∇Un，∇vh）]

[=-（f（Un1）-f（Un2），∇vh）] （15）

在式（15）中令[vh=Un]，由式（5）、式（7）及式（8）， 可得

[12Δt[（‖Un‖20-‖Un-1‖20）+α（|Un|21-|Un-1|21）]]

[≤-（f（Un1）-f（Un2），∇Un）≤‖f（Un1）-f（Un2）‖0‖∇Un‖0]

[≤‖f（Un1）-f（Un2）‖0‖∇Un‖0][≤C‖Un1-Un2‖0，4‖Un1][+][Un2‖0，4‖Un‖1+][C‖Un1-Un2‖0‖Un‖1][≤C‖Un‖0，4‖Un‖1][+C‖Un‖0‖Un‖1≤C‖Un‖21，]

不等式两边同时乘以[2Δt]并求和，由离散的Gronwall引理[13-14][U0=0]，可得[‖Un‖21=0，]结论得证。

值得注意的是，本文中[C]表示一个和网格尺寸[h]以及时间步长[Δt]均无关的正常数，不同的地方取值不一样。

3 超逼近和超收敛分析

本节我们讨论能量稳定格式下的超逼近和整体超收敛结果。

首先，给出双线性元的一些高精度结果。

引理2[[15]] 对任意的[vh∈Vh]，有

[‖u-Ihu‖0，p≤Ch2‖u‖2，p，u∈W2，p（Ω）]" [（16）]

[（∇（u-Ihu），∇vh）≤Ch2‖u‖3‖vh‖1，][u∈H3（Ω） ] [ （17）]

其次，我们可以证明如下的超逼近性质。

定理3 设[un]和[Unh]分别为方程（2）和（3）的解，当[u∈L∞（0，T；H3（Ω）），][ut∈L2（0，T；H3（Ω）），][utt∈L2（0，T；H1（Ω））]时，有

[‖Ihun-Unh‖1≤C（h2+Δt）] [（18）]

证明： 令[un-Unh=un-Ihun+Ihun-Unh=ξn+ηn。]则由方程（2）和（3）可得误差方程为：

[（∂tηn，vh）+α（∇∂tηn，∇vh）+β（∇ηn，∇vh） =-（∂tξn，vh）-α（∇∂tξn，∇vh）-β（∇ξn，∇vh）+" " " "（f（Unh）-f（un），∇vh）-（Rn1，vh）-α（∇Rn1，∇vh）" " （19） ]

其中，[Rn1=unt-∂tun=1Δttn-1tn（τ-tn-1）utt（τ）dτ]。

在式（19）中令[vh=ηn]，则有

[（∂tηn，ηn）+α（∇∂tηn，∇ηn）+β（∇ηn，∇ηn） =-（∂tξn，ηn）-α（∇∂tξn，∇ηn）-β（∇ξn，∇ηn）+（f（Unh）-f（un），∇ηn）-（Rn1，ηn）-α（∇Rn1，∇η）" " " " " " " =i=16Ai" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " "（20）]

容易验证

[（∂tηn，ηn）≥12Δt（‖ηn‖20-‖ηn-1‖20）α（∇∂tηn，∇ηn）≥α2Δt（|ηn|21-|ηn-1|21）] （21）

利用泰勒公式展开，截断误差可估计为

[|A5+A6|=|（Rn1，ηn）+α（∇Rn1，∇ηn）|]

[≤CΔttn-1tn‖utt‖21dτ+C‖ηn‖21] （22）

由引理2可得

[|A1+A2+A3|" " " " " " " " " " " " " " " " " " " " " " " " " " " " "=|（∂tξn，ηn）+α（∇∂tξn，∇ηn）+β（∇ξn，∇ηn）|" ≤Ch4（1Δttn-1tn‖ut‖23dτ+‖un‖23）+C‖ηn‖21" " "（23）]

下面我们主要估计非线性项[A4]。

[|A4|=|（f（Unh）-f（un），∇ηn）|][=|（12（（un）2-（Unh）2），∇ηn）+（un-Unh，∇ηn）|][≤C‖un-Unh‖0，4‖un+Unh‖0，4‖ηn‖1+C‖un-Unh‖0‖ηn‖1]

[≤C‖ξn+ηn‖0，4‖ηn‖1+C（‖ξn‖0+‖ηn‖0）‖ηn‖1≤Ch4‖un‖22，4+C‖ηn‖21≤Ch4‖un‖23+C‖ηn‖21" " " " " （24）]

将式（21）—（24）代入式（20），可得

[12Δt[（‖ηn‖20-‖ηn-1‖20）+α（|ηn|21-|ηn-1|21）]≤Ch4（‖un‖23+1Δttn-1tn‖ut‖23dτ）+" " " " " " " " " CΔttn-1tn‖utt‖21dτ+C‖ηn‖21" " " " " " " " " " " （25）]

不等式两边同时乘以[2Δt]并求和，注意到[η0=0]，则有

[‖ηn‖21≤Ch4（Δti=1n‖ui‖23+0T‖ut‖23dτ）+C（Δt）20T‖utt‖21dτ+CΔti=1n‖ηi‖21] （26）

选取足够小的[Δt]使得[1-CΔtgt;0]，并利用离散的Gronwall引理[13-14]，可得

[‖ηn‖21≤Ch4（‖u‖2L∞（0，T；H3（Ω））+0T‖ut‖23dτ）+C（Δt）20T‖utt‖21dτ≤C（h4+（Δt）2），]

结论得证。

为了得到整体超收敛结果，利用文献[14]中的思想，我们将相邻的四个小单元[K1，K2，K3，K4]合并为一个大单元[K]，即[K=i=14Ki]，相应的剖分记为[T2h]，相应的插值算子[I2h]满足如下性质：

[I2hIhu=I2hu， ‖I2hu-u‖1≤Ch2‖u‖3，‖I2hvh‖1≤C‖vh‖1， ∀ vh∈Vh] （27）

令[un-I2hUnh=un-I2hIhun+I2hIhun-I2hUnh]，利用式（18）、式（27）和三角不等式，我们有下面的整体超收敛结果：

定理4 在定理3的假设下，有下列式子成立：

[‖un-I2hUnh‖1≤C（h2+Δt）] （28）

4 数值例子

本节我们考虑如下的BBMB方程：

[ut-Δut-Δu-∇⋅f（u）=g（t，X）， （X，t）∈Ω×（0，T]，u（X，t）=0， （X，t）∈∂Ω×（0，T]，u（X，0）=u0（X）， X∈Ω，]

其中，[Ω=[0，1]×[0，1]，]将[Ω]剖分为[m×n]矩形网格，精确解定义为[u（x，y，t）=（1+e-t）xy（x-1）（y-1）]。

首先，在图1中给出能量[En]的曲线图，这里[t∈[0，0.1]，h=120，Δt=1.0e-05，]从图1 中我们可以看出能量是稳定的，和定理1的结论相吻合。

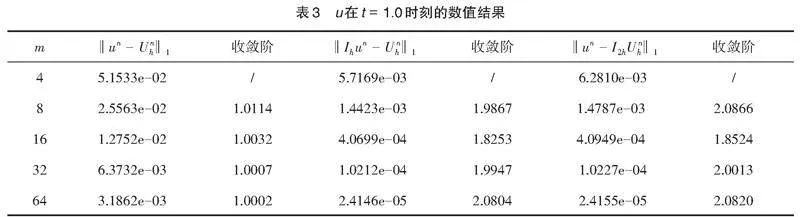
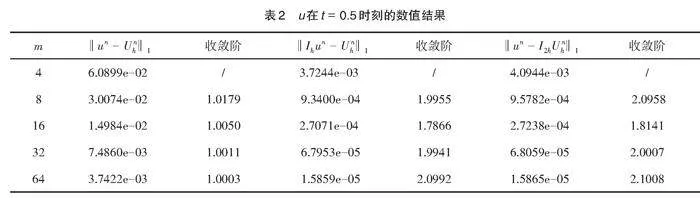
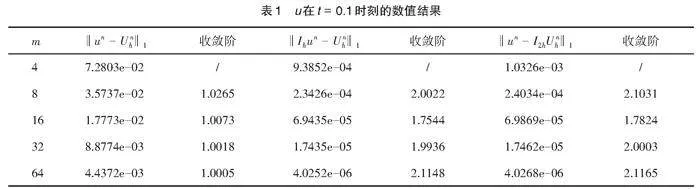
其次，我们分别在表1—表3中给出[t=0.1、 0.5]和[1.0]时刻下的收敛性、超逼近和超收敛结果，为了得到收敛阶，我们取[Δt=h2]。

从表1—表3中可以看出[‖un-Unh‖1]的收敛阶为[O（h），‖Ihun-Unh‖1]和[‖un-I2hUnh‖1]的收敛阶为[O（h2）]，和我们的理论分析相吻合。

参考文献：

［1］CHENG H， WANG X F. A high-order linearized difference scheme preserving dissipation property for the 2D Benjamin-Bona-Mahony-Burgers equation[J]. J. Math.Anal.Appl.，2021，500（2）：125182.

［2］OMRANI K，MEKKI A.Finite difference discretization of the Benjamin-Bona-Mahony-Burgers equation[J].Numer. Methods Partial Differ. Equ.，2008，24（1）：239-248.

［3］彦刚，马维元，张申贵.BBMB方程的三种新的线性差分格式[J].宁夏大学学报：自然科学版，2013，34（2）：115-120.

［4］KADRI T，et al. Methods for the numerical solution of the Benjamin-Bona-Mahony-Burgers equation[J].Numer.Methods Partial Differ. Equ.，2008， 24 （6）： 1501-1516.

［5］GAO F Z，QIU J X，ZHANG Qiang.Local discontinuous Galerkin finite element method and error estimates for one class of Sobolev equation[J]. J. Sci. Comput.，2009，41（3）： 436-460.

［6］MEHDI D，MOSTAFA A，MOHEBBI A. The use of interpolating element-free Galerkin technique for solving 2D generalized Benjamin-Bona-Mahony-Burgers and regularized long-wave equations on non-rectangular domains with error estimate[J]. J. Comput. Appl. Math.， 2015， 286： 211-231.

［7］SHI D Y，YANG H J. Superconvergence analysis of finite element method for Poisson-Nernst-Planck equations[J]. Numer. Methods Partial Differ. Equ.，2019，35：1206-1223.

［8］LI B Y，SUN W W. Error analysis of linearized semi-implicit Galerkin finite element methods for nonlinear parabolic equations[J].Int.J.Numer.Anal. Model.，2013，10：622-633.

［9］SHI X Y，LU L Z. A new two-grid nonconforming mixed finite element method for nonlinear Benjamin-Bona-Mahoney equation[J]. Appl. Math. Comput.，2020，371：124943.

［10］SHI D Y，WANG J J.Unconditional superconvergence analysis of a Crank-Nicolson Galerkin FEM for nonlinear Schr[o]dinger equation[J].J. Sci. Comput.，2017，72：1093-1118.

［11］CIARLET P G.The finite element method for elliptic problem[M].Amsterdam：North Holland，1978.

［12］KESEVAN S.Topics in functional analysis and applications[M]. New Delhi：Wiley Eastern Limited，1989.

［13］王俊俊. 非线性发展方程无网格比高精度有限元方法研究[D].郑州：郑州大学，2018.

［14］孙月.多重积分有限体积法在工程中若干问题的应用[D].哈尔滨：哈尔滨工程大学，2019.

［15］YAN N N. Superconvergence analysis and a posteriori error estimation in finite element methods[M]. Beijing：Science Press，2008.

责任编校：刘 燕，田 旭

High Accuracy Analysis of an Energy-Stable Fem for Nonlinear Benjamin-Bona-Mahony-Burgers Equation

WANG Lele

（School of Mathematics， Zhengzhou University of Aeronautics， Zhengzhou" 450046， China）

Abstract： In this paper， the high accuracy analysis of an energy-stable fully discrete finite element （FE） scheme for the Benjamin-Bona-Mahony-Burgers （BBMB） equation is studied. Firstly， the stability of energy of backward-Euler （B-E） fully discrete scheme is proved which leads to the boundedness of the FE solution in [H1]-norm. Secondly， the existence and uniqueness of solution for approximation problem are proved by employing the above boundedness and Brouwer fixed-point theorem.Thirdly， by use of the special property of bilinear element， the superclose and global superconvergence results are derived. Finally， a numerical test is given to verify the validity of the theoretical analysis.

Key words： BBMB equation; energy-stable scheme; superclose and superconvergence analysis

收稿日期：2023-12-06

基金项目：河南省高等学校重点科研项目 （22A110025）；河南省科技攻关项目（222102320266）

作者简介：王乐乐，女，河南南阳人，博士，讲师，研究方向为有限元方法。