构建问题“经验链” 发展问题解决能力

【摘" "要】“问题解决”是数学教学的重要内容。在数学教学中引导学生自主构建问题“经验链”，能够帮助学生在发现问题、提出问题、分析问题和解决问题的过程中，发展多样化问题解决的思维、经验及能力，从而使学生能在问题解决的过程中体会其道理，解释计算结果的实际意义，感悟数学与现实世界的关联，形成初步的模型意识和应用意识。

【关键词】问题解决；问题“经验链”；有余数的除法

《义务教育数学课程标准（2022年版）》在第一学段（1～2年级）的目标中明确提出，学生要能“在教师指导下，从日常生活中提出简单的数学问题，尝试运用所学知识和方法解决问题；在解决问题的过程中，感悟分析和解决问题的基本方法，感受数学在生活中的应用”。在第一学段的问题解决中，构建问题“经验链”是指在教师的指导下，基于真实情境发现问题，运用数量关系深入分析，借助比较归纳的方法解决问题，并在检验迁移中反思解决的过程。实现学生问题解决“经验链”的有效构建，可有效促进学生学习力的提升。

在当前的问题解决教学中，存在过程体验不连贯、探究分析不深入、策略运用不熟练、价值感悟不充分等现象。波利亚在《怎样解题》中，将解题过程划分为弄清问题、拟定计划、实现计划和回顾反思四个阶段。因此，让学生全面参与、充分经历问题解决的全过程，积累问题解决的基本经验，就显得至关重要。

一、构建发现问题“经验链”

问题是数学的心脏。在数学学习中，发现问题、提出问题的能力直接影响学生问题解决的水平。学生通常通过读题或读图获取相关信息，并在情境或生活实际中抽象出数学问题。因此，教师应鼓励学生采用多元化的方式，挖掘隐含在问题情境中的各类问题，使学生充分经历问题发现的过程，逐步形成发现问题“经验链”。

（一）情境式：情境发展，感知信息

针对小学生的年龄特点及思维特征，教师在引导学生解决问题时，应致力于创设富有启发性的解题氛围与情境。目前，许多教师已成功运用游戏、故事、角色扮演及现实生活元素等手段创设情境，帮助学生在真实情境中发现问题、提出问题。

例如，在“有余数的除法”教学中，为了使学生深化对余数概念的理解，教师需借助于“分”这一现实情境。因此，本单元的教学设计以“表内除法”中的平均分为基础，进一步探讨分物过程中“均分以后有余”的情况。教学时，教师可直接引入情境：“有10根小棒，用以摆三角形。”学生在这样的情境下自然会提出问题：“能摆多少个三角形？”随着操作的进行，学生会进一步提出问题：“如果小棒有剩余，但不足以摆成一个完整的三角形，该怎么处理？”在揭示剩余小棒即为余数的概念后，学生自然会询问：“余数在书写时该如何表示？”由此，通过情境化的引导，学生在潜移默化中理解了数学问题的本质，并能随着情境的发展自然地提出数学问题。

（二）渗透式：赋予意义，形成意识

学生是学习的主体。在日常教学中，教师应对学生的问题意识进行培养。教师可在帮助学生理解算理的基础上，为算式赋予实际意义，并引导学生运用生活化的数学语言描述问题，从而使其逐步形成问题意识。

在“表内除法”单元的教学中，为渗透问题意识，教师在学生理解除法算理的基础上，结合自己身边的生活情境，为算式赋予了实际意义。以12÷4=3为例，它可以表示把12平均分成4份，每份是3。教师应鼓励学生依据这个算式创编实际问题情境，如“把12个苹果平均分给4个学生，每人可以分到几个？”通过结合实际、赋予意义，使学生逐步学会用数学的眼光观察现实世界。

（三）生活式：联系生活，提炼问题

数学来源于生活，又应用于生活。从生活故事中寻找问题，是基于学生生活经验及认知经验进行教学的适宜场域。教师应引导学生将生活经验“数学化”，从中提炼数学问题，使问题具有指向性与目的性。

在日常生活中，学生皆有过“分零食”的经历，且经常会遇到零食“平均分后有余”的情况。在教学中，教师可利用分糖果情境开展小组合作活动。例如，将一定数量的糖果平均分给每名同学，每人可分到3颗糖果，据此可列出四个算式：12÷3=4（人）、13÷3=4（人）……1（颗）、14÷3=4（人）……2（颗）、15÷3=5（人）。在教学反馈环节，教师提问：“你们能提出什么数学问题？”学生观察后提出“余数总是1和2吗？”“余数的变化是不是存在规律？”等问题。从生活经验出发，重在“提炼”的过程。除了要让学生经历完整的活动，还要引导学生关注余数的变化情况，提高所提问题的针对性。

二、构建分析问题“经验链”

分析问题是问题解决的必备条件。教师应引导学生从已知信息之间的关系出发，逐步分析已知信息与求解问题之间的关系。在此过程中，审题是基础，使用什么策略进行分析是关键。针对第一学段学生的年龄特点及思维特征，可启发学生通过圈关键字词、画示意图、操作记录等方式分析问题，逐步构建分析问题的“经验链”。

（一）圈关键字词，深化题意理解

当问题陈述的语言表述发生变化时，学生解读信息时可能会遇到困难。故教师需要引导学生养成仔细读题和耐心思考的习惯，抓住题目中的关键字、词或句，准确理解其表达的意义。

例如，在解决“烘焙小组做了22块蛋黄酥，要装到盒子里。每个盒子最多装4块，他们至少需要准备多少个盒子？”的问题时，教师要引导学生将“最多装4块”和“至少需要”两个关键词圈起来，并深入理解“最多装4块”表示“每盒可以装4块、3块、2块、1块”，“至少需要”表示“最少需要准备几个盒子”，从而培养学生在分析问题时仔细推敲、咬文嚼字的能力，真正理解题意。

（二）画示意图，实现思维可视化

对于一些数量关系比较复杂或需较高观察、推理意识的题目，应鼓励学生采用画直观示意图的方式进行分析，并用他们喜欢的方式呈现分析问题的过程。以此实现学生思维的可视化，进而促进其解答方法的多样化，同时也为学生优化解答策略提供思维准备，使其充分体验问题解决的过程，获得成就感。

例如，在“用有余数除法的知识解决与按规律排列有关的问题”的教学中，教师出示题目（如图1）后，学生会主动采用多种方法解决问题。方法一：依照已有图形的规律继续画下去，直至画到第16面旗帜，从而确定其颜色。方法二：在图1的旗帜下方标注数1、2、3、4、5……写到数16所对应的旗帜，进而确定颜色。方法三：将3面旗帜为一组圈在一起，圈完4组后，根据规律，第5组需要从头开始圈，确定第16面旗帜就是第6组的第1面旗帜，从而确定其颜色。方法四：根据除法算式16÷3=5（组）……1（面），利用余数确定第16面旗帜的颜色。可见，从方法一到方法四，学生解决问题的方法逐步接近教学目标，这为后续优化方法、达成共识奠定了思维基础。而在这个教学过程中，学生运用画图策略分析问题的能力也得到了显著提升。

（三）操作记录，分解概念

在第一学段的数学教学中，让学生动手操作并及时记录，有助于加深其对概念的理解。

例如，在解决“用10根小棒摆三角形”的问题时，教师先让学生独立摆一摆。随后，将操作过程分解为五个步骤：第一步，准备10根小棒（即要分的小棒总数）；第二步，思考怎么分（就是求10里面有几个3，用除法计算）；第三步，拿出3根小棒摆一个三角形（即一个3）；第四步，继续摆三角形，直到剩余小棒无法再摆一个三角形（发现可以摆3个三角形，即3个3）；第五步，将最后1根小棒放边上（表示还多出1根）。

通过详尽记录这五个步骤，学生不仅清楚了分的过程，还能深入体会算式中每个数的来源与含义。这样的方式有助于学生充分理解余数的含义，认识到有余数除法的实际意义，实现对除法解决问题认知的跨越。此外，及时记录还能培育学生的符号意识。

三、构建解决问题“经验链”

在问题解决教学中，教师应引导学生辨析题目，优化方法，发展模型意识，以提升学生问题解决的综合能力，发展他们的核心素养。为实现这一目标，教师可以采用对比分析、讨论交流、变换问题等教学方式，引导学生自主提炼问题解决方法，逐步学会对比、归纳和应用，有效构建解决问题“经验链”。

（一）对比分析

在“有余数的除法”单元，教材中的例题和习题体现了平均分的两种情况——包含和等分。为了区分这两者的意义，教师可以借助对题组的对比分析，加深学生对其的理解。

例如，教师可呈现以下题组。

（1）17颗草莓，每人分5个，可以分给几人？还多几颗？

（2）17颗草莓，平均分给3人，每人分到几颗草莓？还多几颗？

学生在经历分的过程后，就能理解这两个算式虽然看起来相似，但实际意义截然不同，其算式的含义也不同。

（二）讨论交流

问题解决的方法策略可以是多样化的，但在多样化的基础上，教师还应引导学生通过反复尝试、讨论，寻找便捷、高效的方法，提高问题解决的效率。

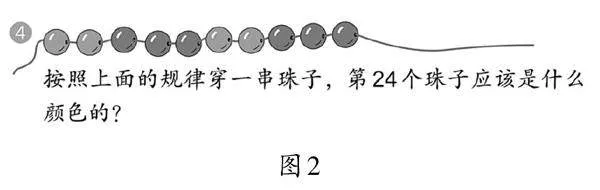
例如，在学习了“用有余数除法的知识解决与按规律排列有关的问题”之后，部分学生仍不会选择用有余数的除法算式解决问题。此时，教师可继续出示练习十五中的第4题（如图2）。

在这一问题的基础上，教师可进一步提问：“第44颗珠子是什么颜色？第99颗呢？”随着数不断变大，此时再讨论用除法算式解决问题的便捷性，学生便会充分认可算式是相对最优的解决方法。如此教学，在保证前期算法多样化的基础上，使问题解决策略有了新发展，更能让学生体会数学学科的简约、高效之美。

（三）变换问题

第一学段学生的年龄较小，在解决问题时容易受思维定式的影响。为此，教师可以通过变换问题的方式，帮助学生形成一类问题的解决策略，增强他们灵活选择策略解决问题的能力。变换问题的思路应强调意义理解、算法优化或形式多样的数学表达，旨在帮助学生形成某一类问题的解决思路，或是区分不同类型问题的不同特点，发展初步的模型意识。

四、构建反思问题“经验链”

反思问题是问题解决的重要环节。在学生得到问题的答案后，教师应引导他们对结果进行反思，进而积累问题解决的经验。这对低年级学生来说尤为关键。

（一）反思过程

教师需引导学生对问题解决过程进行回顾与审视，如回顾运用了哪一种运算来解决问题，为什么要采用这种运算方式。

例如，在“用有余数除法的知识解决简单的实际问题”的反思环节，针对“至少要准备多少个盒子”的问题（如图3），教师应引导学生反思“为什么用除法解答？”“计算是否正确？”以此深化学生对除法含义的理解，并鼓励学生思考验证方法，如通过乘法算式验证答案的正确性。这一过程有助于培养学生回顾反思的习惯，促进问题解决教学中反思问题“经验链”的形成。

（二）迁移方法

在问题解决的教学中，教师应逐步引导学生思考：“这个方法是否可行？”“能否找到更好的方法？”“应该从哪些方面来寻找更好的方法？”以此培养学生解决问题的灵活性，并发展他们跨学科问题的解决能力。

总之，无论是在数学问题解决还是跨学科问题解决中，发展学生的创新意识和培养拔尖创新人才都需要经历利用真实情境发现问题，通过数量关系分析问题，借助比较归纳解决问题，以及在迁移应用中反思问题的解决过程。而将数学问题解决教学中的这些问题“经验链”有效迁移应用到跨学科项目化学习中，将有助于学生应用意识与创新能力的全面发展。

参考文献：

［1］波利亚.怎样解题：数学思维的新方法［M］.涂泓，冯承天，译.上海：上海科技教育出版社，2011.

［2］焦尔当.学习的本质［M］.杭零，译.上海：华东师范大学出版社，2015.

［3］史宁中.基本概念与运算法则：小学数学教学中的核心问题［M］.北京：高等教育出版社，2013.