解直角三角形在解决实际问题中的应用探究
黄天纪
[摘 要]在现实生活中,有很多和解直角三角形相关的实际问题。教师应引导学生应用解直角三角形的相关知识解决这些实际问题,以培养学生的数学建模、数学抽象素养。文章结合典型例题,探讨解直角三角形在解决实际问题中的应用,旨在帮助学生理解解直角三角形的常见概念及模型,找到解题突破口,培养学生解决实际问题的能力和数学核心素养。
[关键词]解直角三角形;实际问题;应用
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2024)14-0033-03
《义务教育数学课程标准(2022年版)》明确指出,通过经历独立的数学思维过程,学生能够分析、解决简单的数学问题和实际问题。由此可见,培养学生解决实际问题的能力,成为新时代数学课程改革的重要内容。在解决实际问题的过程中,学生常遇到这样的困境:不会结合数学知识把现实生活问题转化为数学问题,解题无从下手。本文结合典型例题,探讨解直角三角形在解决实际问题中的应用,以培养学生解决实际问题的能力和数学核心素养。
一、解直角三角形的常见概念及模型
(一)常见概念
1.仰角、俯角——观察者的视线与水平线所形成的夹角,即视线高于水平线所形成的角叫仰角,视线低于水平线所形成的角叫俯角。
2. 方向角——以观测点O为中心,过观测点作一条水平线和一条铅垂线,表示南北方向的铅垂线,与观测点到目的地之间的连线所形成的夹角叫方向角。
3. 坡角、坡度——水平面与坡面所形成的夹角叫坡角,而坡度就是坡面的铅直高度与坡面的水平宽度的比值。
4.直角三角形五个元素之间的关系:(1)三边关系(勾股定理);(2)两角关系(两个锐角互余);(3)边角关系(锐角三角函数)。在这五个元素当中,已知其中两个元素(必须有一个元素是边),就可以求出其余未知的三个元素。
(二)常见模型
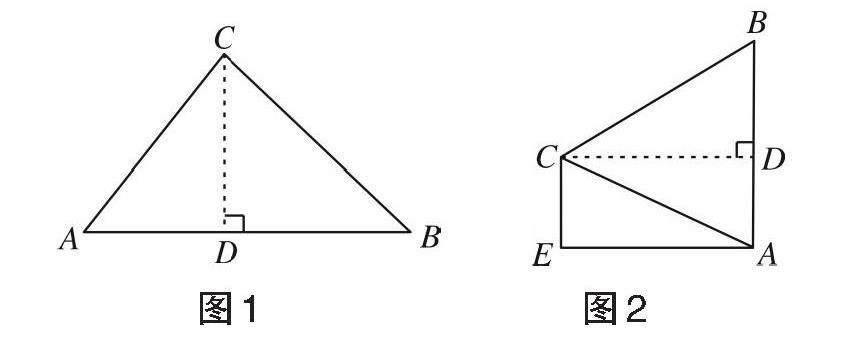
模型1:背靠背模型(如图1、图2)。
图1 图2
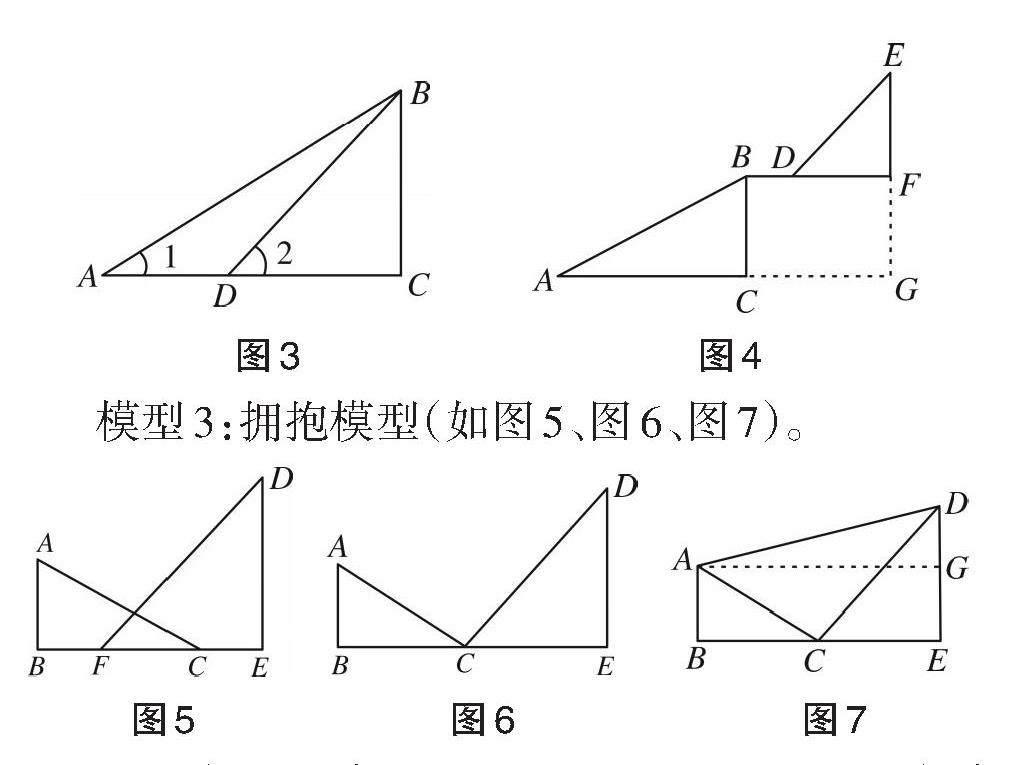
模型2:母子模型 (如图3、图4)。
图3 图4
模型3:拥抱模型(如图5、图6、图7)。
图5 图6 图7
二、应用解直角三角形解决实际问题的基本思路
(一)基本思路
应用解直角三角形解决实际问题的基本思路:首先将实际问题转化为数学问题(含解直角三角形),即舍去实际事物的具体内容,把事物及它们的联系转化为图形(含点、线、角等元素);然后对数学问题进行解答,得出的数学问题的解即为实际问题的解。
(二)具体步骤
(1)理解题干中出现的数学概念和意义,如前面提及的仰角、坡角等,根据题干的问题描述,画出对应的平面图形,将实际问题转化为数学问题;(2)将数学问题与解直角三角形知识建立联系,并利用直角三角形的边角关系构造等式、解答问题(对于锐角或钝角的非直角三角形,可先采用辅助线法,将它们分割或补充,构造出直角三角形或矩形);(3)找出与解题有关的直角三角形,并解这些三角形,最后得到答案。
三、解直角三角形在解决实际问题中的应用例析
在应用解直角三角形知识解决实际问题时,要将实际问题转化为数学问题,将实际问题中的数量关系转换为直角三角形的边角关系,结合图形、已知条件、所求问题展开联想,寻找条件与问题之间的逻辑关系或转化关系,利用解直角三角形知识解决问题。若所给图形不是直角三角形,应添加辅助线,构造出直角三角形。若有两个或两个以上的三角形,且不能直接求解,则可以考虑分别由两个三角形找出含有相同元素的关系式,运用方程知识求解。本文主要探讨应用解直角三角形解决有关仰角俯角、方位角、坡角坡度问题的方法。
(一)应用解直角三角形解决仰角俯角问题
解决仰角俯角问题,关键是弄清仰角和俯角的定义,根据题意画出含有仰角和俯角的几何图形,将实际问题中的数量关系转换为直角三角形的边角关系,也就是将已知数据在几何图形中标出,再利用解直角三角形知识求解。
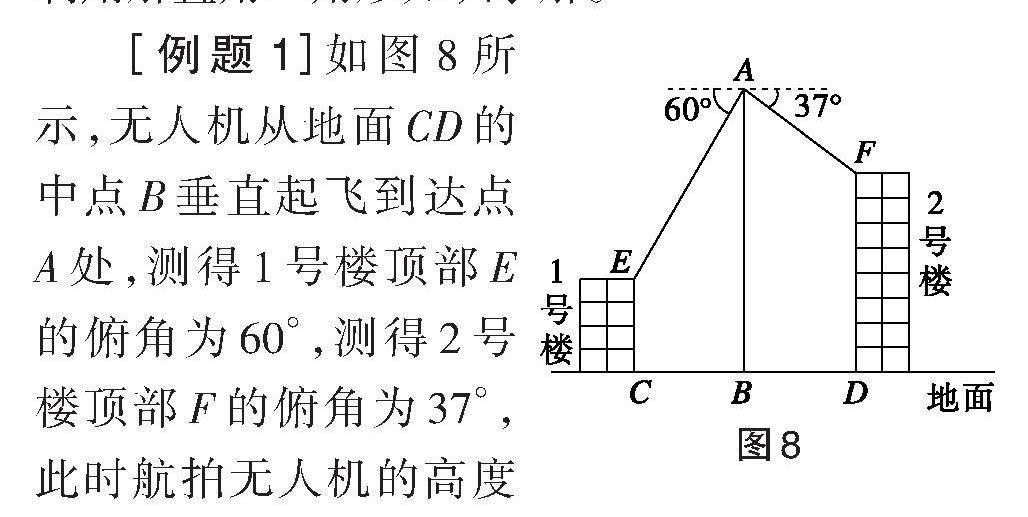
[例题1]如图8所示,无人机从地面[CD]的中点[B]垂直起飞到达点[A]处,测得1号楼顶部[E]的俯角为60°,测得2号楼顶部[F]的俯角为37°,此时航拍无人机的高度为60米,已知1号楼的高[CE]为20米,求2号楼的高[DF]。(结果精确到1米;参考数据[sin37°≈0.60],[cos37°≈0.80],[tan37°≈0.75],[3≈1.73],[2≈1.41])
【分析】过点[E]、[F]分别作[EM⊥AB],[FN⊥AB],垂足分别为[M]、[N],通过添加辅助线构造两个直角三角形,将实际问题中的数量关系转换为直角三角形的边角关系。由题意可得,在[Rt△AEM]中,[AM=40],[∠AEM=60°],已知两个条件(一边一角),可以求出其他的边和角,用锐角三角函数求出[EM],再运用矩形、中点性质求出[NF],再转换到解[Rt△AFN]。由题意可得[∠AFN=37°],在Rt[△AFN]中又找到两个已知条件(一边一角),可用锐角三角函数求出[AN],最后用线段和差求出[DF=BN=AB-AN]。
【详解】如图9所示,过点[E]、[F]分别作[EM⊥AB],[FN⊥AB],垂足分别为[E]、[F],由题意得[BM=CE=20],[∠AEM=60°],[∠AFN=37°],[CB=DB=EM=FN],[AB=60],∴[AM=AB-MB=60-20=40],
在[Rt△AEM]中,∵[tan∠AEM=AMEM],∴[EM=AMtan60°=403≈401.73≈23.12],∴[FN=EM=23.12]。
在[Rt△AFN]中,∵[tan∠AFN=ANFN],∴[AN=tan37°],[AN=tan37°×23.12≈0.75×23.12=17.34],∴[DF=BN=AB-AN≈60-17.34≈43]。
答:2号楼的高[DF]约为43米。
【培养目标】引导学生应用解直角三角形知识解决仰角俯角问题,帮助学生理解仰角和俯角的概念,使学生能够熟练应用三角函数解直角三角形;通过指导学生添加辅助线构造直角三角形,让学生学会把实际问题转化为数学问题,培养学生的数学建模、数学运算、数学抽象等核心素养。
(二)应用解直角三角形解决方位角问题
解决有关方位角的问题,关键是弄清方位角的定义,画出有方位角的几何图形。如题图为非直角三角形,则需添加辅助线,构造直角三角形和矩形,将实际问题中的数量关系转换为直角三角形的边角关系,再利用解直角三角形知识求解。
[例题2]在东西走向笔直的限速公路上,规定汽车的最高行驶速度不能超过60 km/h(即[503 ]m/s),交通管理部门在离该公路正南方向100米[A]处设置了速度检测点,以东西向[BC]为[x]轴,以南北向为[y]轴建立如图10所示的平面直角坐标系,[A]位于[y]轴上,测速路段[BC]在[x]轴上,点[B]在点[A]的北偏西60°方向上,点[C]在点[A]的北偏东45°方向上。一辆汽车从点[B]匀速行驶到点[C]所用时间为15 s。请你通过计算,判断该汽车在这段限速公路上是否超速。([3]取1.7)
[A(0,-100)][x/m][y/m][B][O][C]
图10
【分析】在直角三角形[ABO]和直角三角形[ACO]中,分别找出两个已知条件(一边一角),即[AO=100]和[∠OAB=60°];[AO=100]和[∠OAC=45°],可利用锐角三角函数求出[OB]和[OC]的长,从而求出[BC=OB+OC],也就是求出限速路程,由此求出速度,即可解答。
【详解】∵在直角三角形[ABO]中,[AO=100],[∠BAO=60°],∴[OB=OA·tan60°=1003],
∵[△AOC]是等腰直角三角形,
∴[OC=OA=100],
∴[BC=OB+OC=1003+100≈270],
∵[270÷15=18],
[18>503],
∴该汽车在这段限速公路上超速了。
【培养目标】引导学生应用解直角三角形知识解决方位角问题,帮助学生理解方位角的概念,使学生能够熟练应用三角函数解直角三角形。通过指导学生画出几何图形,培养学生把实际问题转化为数学问题的能力,提升学生的数学建模素养及分析与解决问题的能力。
(三)应用解直角三角形解决坡角坡度问题
解决坡角坡度问题,关键是弄清坡角、坡度、垂直距离、水平距离的定义,根据题意构造出有坡角和坡度的几何图形。若图形是非直角三角形,则需添加辅助线,构造直角三角形和矩形,再利用解直角三角形知识求解。
[例题3]贵州旅游资源丰富。某景区为给游客提供更好的游览体验,拟在如图11所示的景区内修建观光索道,设计示意图如图12所示,以山脚[A]为起点,沿途修建[AB]、[CD]两段长度相等的观光索道,最终到达山顶[D]处,中途设计了一段与[AF]平行的观光平台[BC]为50 m。索道[AB]与[AF]的夹角为15°,[CD]与水平线夹角为45°,[A、B]两处的水平距离[AE]为576 m,[DF⊥AF],垂足为点[F]。(图中所有点都在同一平面内,点[A]、[E]、[F]在同一水平线上。结果精确到1 m。参考数据:[sin15°≈0.25],[cos15°≈0.96],[tan15°≈0.26],[2≈1.41])
(1)求索道[AB]的长;
(2)求水平距离[AF]的长。
图11 图12
【分析】(1)在直角三角形[ABE]中,找出两个已知条件(一边一角),即[AE=576]和[∠BAE=15°],可利用锐角三角函数求出索道[AB]的长度600米,所以[AB=CD=600]。(2)要求[AF]的长度,可添加辅助线,作[CG]垂直[DF],垂足为[G],构造直角三角形[DCG],在直角三角形[DCG]中找出两个已知条件(一边一角),即[CD=600]和[∠DCG=45°],利用锐角三角函数或勾股定理求出[CG],从而求出[AF=AE+BC+CG]。
【详解】(1)在直角三角形[ABE]中,[AE=576],[∠BAE=]15°,∴ [AB=AEcos15°=5760.96=600]。
(2)如图13,作[CG]垂直[DF],垂足为[G],在直角三角形[DCG]中,[CD=AB=600],[∠DCG=45°],∴[CG=CDcos45°=600×22=600×1.412=423],∴[AF=AE+BC+CG=576+50+423=1049]。
【培养目标】引导学生利用解三角形知识解决坡角坡度问题,帮助学生理解坡角和坡度的概念,熟悉应用锐角三角函数和勾股定理解决实际问题。通过引导学生审题、分析问题,使学生掌握数形结合思想,提升学生的直观想象、数学抽象等核心素养。
应用解直角三角形解决仰角俯角、方位角、坡角坡度问题,要熟练掌握解题思路与方法,把握解题关键,找准解题切入点。
总之,解直角三角形是初中数学的核心内容,解直角三角形在解决实际问题中的应用是中考必考点。本文探讨解直角三角形在解决实际问题的应用,帮助学生掌握解决实际问题的数学思想方法,提升学生的解决问题能力和数学核心素养。
[ 参 考 文 献 ]
[1] 黄金珠.解直角三角形在解决实际问题中的应用[J].数理天地(初中版),2023(9):28-29.
[2] 梁海栗.核心素养导向下的初中数学解题教学策略研究[J].中学教学参考,2023(2):10-12.
[3] 赵芳.论相似三角形在实际生活中的应用[J].中学教学参考,2023(29):13-15,25.
[4] 王志刚.逆向思维在初中数学解题中的应用[J].中学教学参考,2023(29):4-6.
[5] 中华人民共和国教育部.义务教育数学课程标准:2022年版[M].北京:北京师范大学出版社,2022.
(责任编辑 黄春香)

